Bell-Ford算法思想

对一个点的松弛操作，就是找到经过这个点的另外一条路径（多走一条边），使得花费的代价更小。
如果一个图没有负权环，从一点到另外一点的最短路径，最多经过所有的V个顶点，有V-1条边。
那么对所有点进行 V - 1次松弛操作，理论上就找到了从源点到其它所有点的最短路径。

如果还可以继续松弛，那么说明图中有负权环。

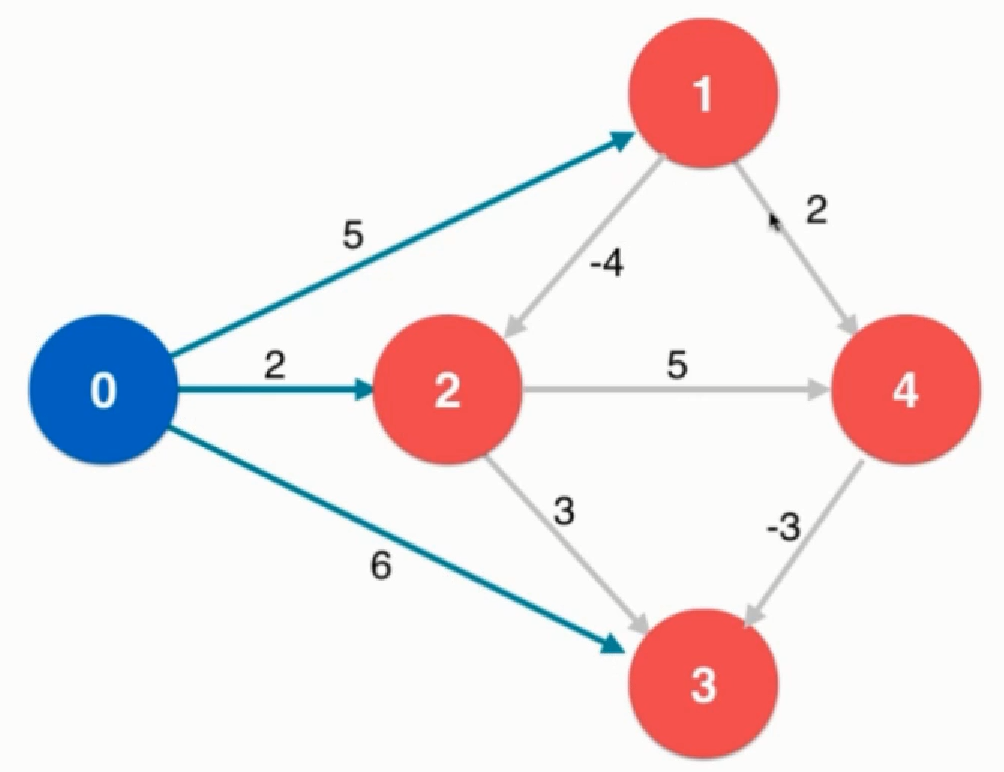
算法实现

有$n$个顶点和$m$条边的图求最短路：

• 从起点经过不超过n条边走到每个点的最短距离：
  1. 备份dis[]到backup[]，目的是使用上次的最短距离更新当前最短距离，防止发生串联
  2. 遍历每条边，$a\to b$
     • $a,b,w$ 即点a到点b的距离为w
     • 使用边$a\to b$来缩短$b$点到起点的最短距离，dis[b] = min(dis[b], backup[a]+w)
• 如果dis[n] < 无穷大，则dis[n]为起点到n点的最短距离；否则不存在最短距离

时间复杂度

Bellman-Ford算法的时间复杂度为$O(n\times m)$

算法应用

1. 求没有负权环的单源最短路径
2. 求最多经过k条的单源最短路径
3. 将边权取反，可以求没有负权环的单源最长路径
4. 判断是否有负权环，由于效率不高，所以通常用SPFA来判断是否存在负环

练习

有边数限制的最短路

代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 510, M = 10010, MAXN = 0x3f3f3f3f;

//边，表示点a到点b的距离为w
struct edge{
    int a, b, w;
}ed[M];

//使用backup[]备份dis[]
//使用之前的最短距离更新当前最短距离，防止发生串联
int dis[N], backup[N];

int n, m, k;

void bellman_ford(){
    memset(dis, 0x3f, sizeof dis);
    dis[1] = 0;
    //循环k次求经过不超过k条边走到每个点的最短距离
    for(int i = 1; i <= k ; i ++){
        memcpy(backup, dis, sizeof dis);
        for(int j = 1; j <= m; j ++){ //遍历每条边，进行松弛
            int a = ed[j].a, b = ed[j].b, w = ed[j].w;
            dis[b] = min(dis[b], backup[a] + w);
        }
    }
}

int main(){
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1; i <= m; i ++){
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        ed[i] = {a, b, w};
    }
    bellman_ford();
    //在松弛过程中可能会改变到n点最短距离，但实际并不存在到n点的最短路径
    if(dis[n] < MAXN / 2) cout << dis[n];
    else puts("impossible");
    return 0;
}