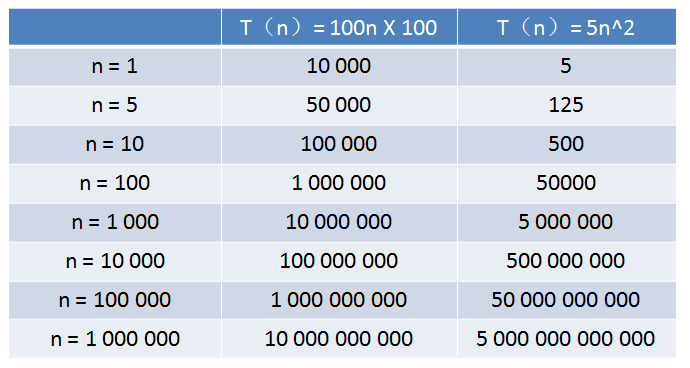
好屌的题

F-至至子的公司排队_牛客小白月赛55 (nowcoder.com)

题意：

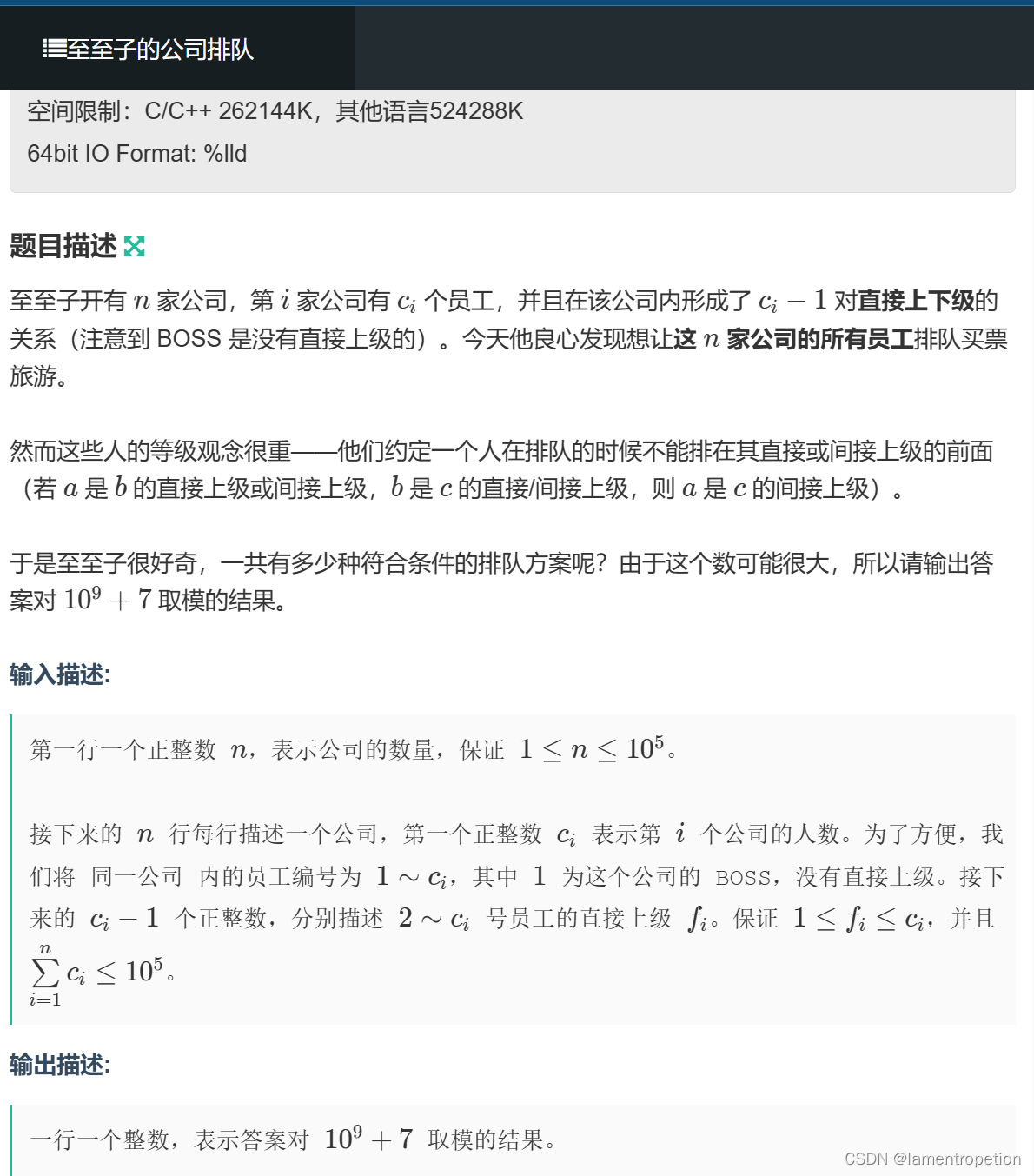
思路：

其实题目问的就是，森林的拓扑序有几种

那么我们先去考虑一棵树的拓扑序有几种

这个可以用树形DP来解决

设dp[u]为，以u为根的子树的拓扑序的种类数，然后去考虑它的子树

关于计数类的树形DP，都可以把一棵子树的所有状态想象成一列，然后多棵子树进行匹配（乘法原理）

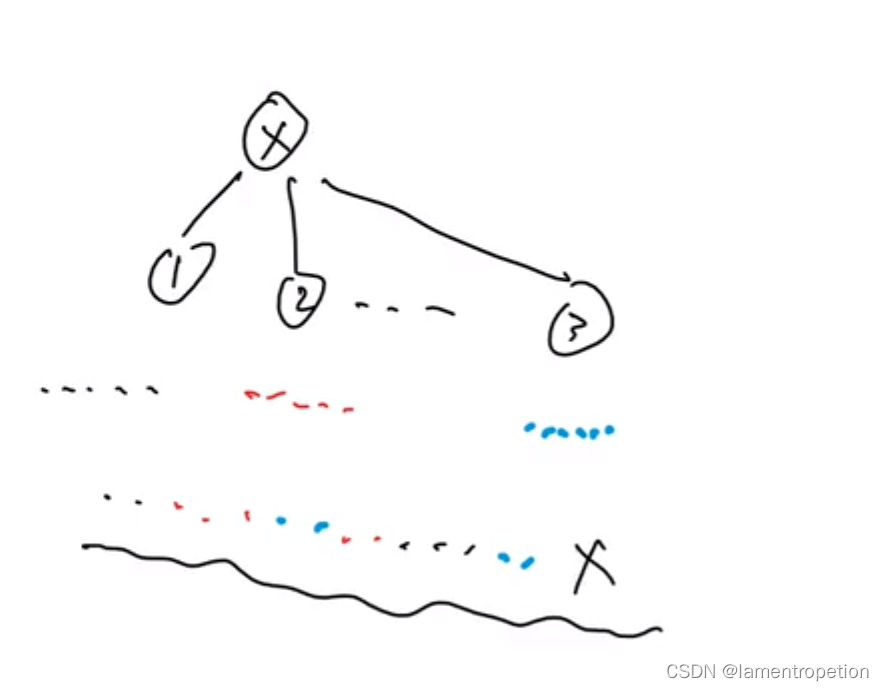
 对于这道题，答案就是这样的：

 

 先是乘法原理把所有儿子的dp值乘起来，然后注意到对于同一棵子树的拓扑序而言，顺序是确定的，因此同一棵子树的拓扑序可以看作是同一颜色的，因此可以看成是可重集排列

这点很重要，我根本没想到这点qwq

那么森林的方案数怎么求呢？其实就是把这么多棵树看作子树，再求一下可重集排列即可

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

using i64 = long long;

const int mxn=1e5+10;
const int mxe=1e5+10;
const int mod=1e9+7;

int N,n,x,tot=0,ans=1,sum=0;
int Fac[mxn],inv[mxn];
int head[mxn],sz[mxn],dp[mxn];

struct ty{
    int to,next;
}edge[mxe<<2];

int ksm(int a,int b,int mod){
    int res=1;
    while(b){
        if(b&1) res=(res*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return res;
}
void F_init(){
    Fac[0]=1ll;
    for(int i=1;i<mxn;i++) Fac[i]=(Fac[i-1]*i)%mod;
    inv[0]=1;
    inv[mxn-1]=ksm(Fac[mxn-1],mod-2,mod);
    for(int i=mxn-2;i>=1;i--) inv[i]=inv[i+1]*(i+1)%mod;
}
void add(int u,int v){
    edge[tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot++;
}
void G_init(){
    tot=0;
    for(int i=0;i<=n+10;i++){
        head[i]=-1;
        sz[i]=dp[i]=0;
    }
}
void dfs(int u,int fa){
    sz[u]=1;
    dp[u]=1;
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        dfs(edge[i].to,u);
        sz[u]+=sz[edge[i].to];;
        dp[u]=(dp[u]*dp[edge[i].to])%mod;
        dp[u]=(dp[u]*inv[sz[edge[i].to]])%mod;
    }
    dp[u]=(dp[u]*Fac[sz[u]-1])%mod;
}
void solve(){
    cin>>N;
    for(int i=1;i<=N;i++){
        cin>>n;
        G_init();
        sum+=n;
        for(int j=2;j<=n;j++){
            cin>>x;
            add(j,x);
            add(x,j);
        }
        dfs(1,0);
        ans=(ans*dp[1]%mod*inv[n])%mod;
    }
    ans=(ans*Fac[sum])%mod;
    cout<<ans<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    F_init();
    while(__--)solve();return 0;
}