文章目录
- 算法
- 时间复杂度
- 时间复杂度计算
- 常见的时间复杂度
- 时间复杂度的差异
- 总结
算法
算法(Algorithm)是求解一个问题需要遵循的,被清楚指定的简单指令的集合。
一个算法的评价主要从时间复杂度和空间复杂度来考虑。而时间复杂度是一个函数,定性描述该算法的运行时间,通常用大O符号表示。
常见的时间复杂度有O(1),O(logn),O(n),O(n2),O(2n)…等。
下面就来讲讲时间复杂度是怎么推算出来的吧。
时间复杂度
在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用
大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
时间复杂度计算
我们定义算法中的语句执行次数称为语句频度或时间频度为T(n)。即T(n)表示程序的执行次数 。
方法1执行多少次:
public int method1(){
System.out.println("hello"); //执行1次
return 0; //执行1次
}
没错,它内部一共执行2次。
那么我们来看下面的方法2执行几次:
public int method2(int n){
for(int i = 0; i<n ; i++){
//i = 0 执行1次,i<n 执行n+1次,i++执行n次
System.out.println("hello"); //输出语句执行n次
}
return 1; //return 执行一次
}
对,它一共执行了 3n+3 次。那么对于方法1就有 T(n) = 2;对于方法2就有 T(n) = 3n + 3。
实际的代码肯定比示例中的代码复杂得多,去统计代码的执行次数显然不可能,所以算法一般使用T(n)的渐进估算值来反映代码的执行速度。而这个估算值我们用”时间复杂度”来表示。
所以针对方法1和方法2,如何根据T(n)估算出时间复杂度:
- 对于 T(n) = 2 ,由于T(n)是一个常数,那么时间复杂度可以直接估算为 1 。所以T(n) = 2 的时间复杂度为 1。 用标准的时间复杂度函数表示就是 O(1)。
- 对于T(n) = 3n + 3 ,随着n值得不断增长,常数3相对于3n来说可以忽略不计。而系数一般也会估算成1。相当于去掉了系数和常数,则该时间复杂度为n。 用时间复杂度函数表示就是O(n)。
- 依次推广到如下多项式中: 对于T(n) = 3n^2 + 3n + 3. 随着n值得不断增大,多项式后面的项的增长就远没有n2的增长大,可以直接舍弃低阶项和常数项,则只保留n的次方数最大的那一项,所以它的时间复杂度就为O(n3)。
总结以上规律:
- T(n)是常数:时间复杂度为O(1);
- T(n)不是常数:时间复杂度为O(T(n)的最高次项并且去掉最高次项的系数)。
常见的时间复杂度
方法1的时间复杂度为 O(1):
//时间复杂度为 O(1)
public void m1(){
System.out.println("A");
System.out.println("B");
...
System.out.println("L");
}
方法2的时间复杂度为 O(n):
//时间复杂度为 O(n)
public int method2(int n){
for(int i = 0; i < n ; i++){
System.out.println("a");
}
return 1;
}
方法3 时间复杂度为 O(n^2):
//时间复杂度为 O(n^2)
public void method3(int n){
for(int i = 0; i < n ; i++){
for(int j = 0 ; j < i ; j ++){
System.out.println("a");
}
}
}
方法4的时间复杂度为O(logn):
public void method4(int n){
int i = 1;
while(i<n)
{
i = i * 2;
}
}
从上面代码可以看到,在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。我们试着求解一下,假设循环x次之后,i 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x = log2^n
也就是说当循环 log2^n 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(logn)
方法5的时间复杂度为O(nlogN) :
public void method5(int n) {
for (int m = 1; m < n; m++) {
int i = 1;
while (i < n) {
i = i * 2;
}
}
}
线性对数阶O(nlogN) 其实非常容易理解,将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logN),也就是了O(nlogN)。
一般常见的时间复杂度进行如下排序(由快到慢)。
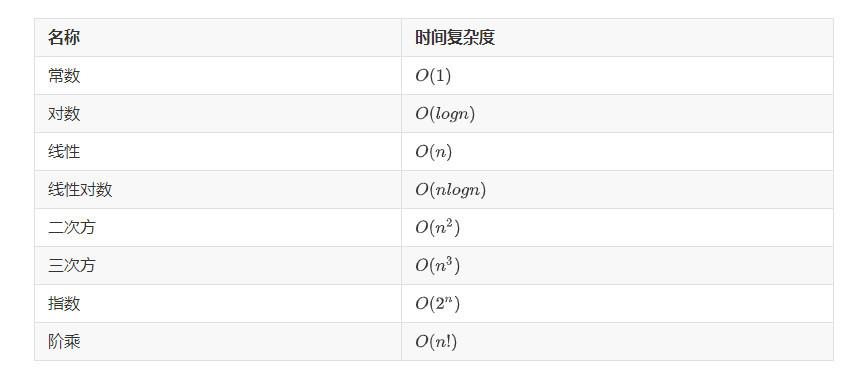
再用曲线图看一下时间复杂度。
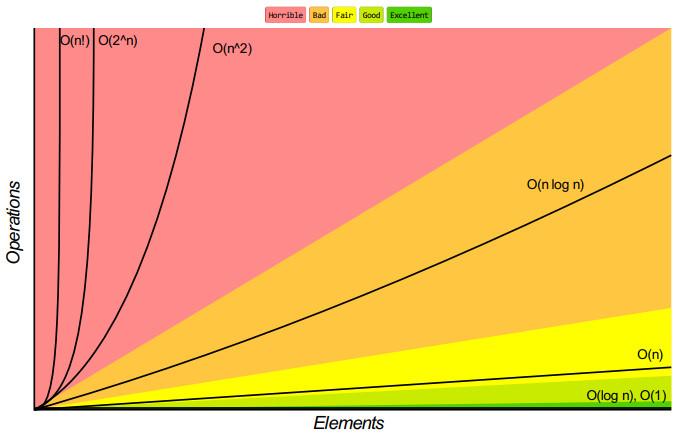
从图中也可以看出,随着元素变多,指数、阶乘级别的增长是最快的。显而易见其执行效率最低。
时间复杂度的差异
我们来举个例子:
算法A的相对时间规模是T(n)= 100n,时间复杂度是O(n)
算法B的相对时间规模是T(n)= 5n2,时间复杂度是O(n2)
算法A运行在老旧电脑上,算法B运行在某台超级计算机上,运行速度是老旧电脑的100倍。
那么,随着输入规模 n 的增长,两种算法谁运行更快呢?
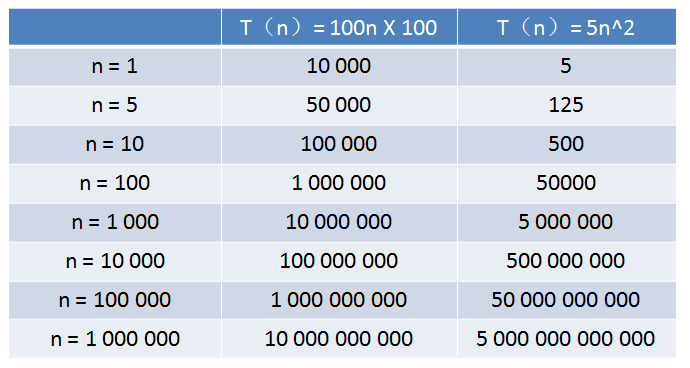
从表格中可以看出,当n的值很小的时候,算法A的运行用时要远大于算法B;当n的值达到1000左右,算法A和算法B的运行时间已经接近;当n的值越来越大,达到十万、百万时,算法A的优势开始显现,算法B则越来越慢,差距越来越明显。
这就是不同时间复杂度带来的差距。
总结
学好算法,则必须要理解时间复杂度这个重要基石。通过以上的分析,相信大家对时间复杂度有了一定的了解,大家共同进步,加油。