在这里插入图片描述

🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:数据结构中有关"二叉树"的知识,用c语言实现,根据前序遍历构建二叉树,前序遍历,中序遍历,后续遍历,以及层序遍历(有点麻烦)等遍历方式.
金句分享:
✨没人爱时专注自己,有人爱时,有能力拥抱彼此!✨

前言

前面,我们在"树的概念"一文中已经介绍过了二叉树的基本概念,二叉树较于线性表(顺序表和链表等),难度有一定提升,主要是要熟练掌握递归,很多有关"二叉树"的操作都需要使用递归算法.

前言
一、"二叉树"的类型声明
二、"二叉树"的遍历
- 3.1 前序遍历:
- 3.2 中序遍历:
- 3.3 后序遍历:
- 3.4 扩展知识:层序遍历(稍复杂)
三、"二叉树"的构造(根据前序遍历)
四、"二叉树"的销毁
五、总代码:
- 声明区(tree.h)
- 队列接口实现区:(Queue.c)
- "二叉树"接口实现区:(tree.c)
- 主测试区:(test.c)

一、"二叉树"的类型声明

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;//数据域
	//指针域
	struct BinaryTreeNode* left;//左子树
	struct BinaryTreeNode* right;//右子树
}BTNode;

二、"二叉树"的遍历

学习二叉树的结构时，最简单的操作是遍历二叉树,所以我们先介绍如何遍历一课二叉树.

二叉树遍历(Traversal):

按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

通俗来讲,就是访问一遍二叉树的所有结点.

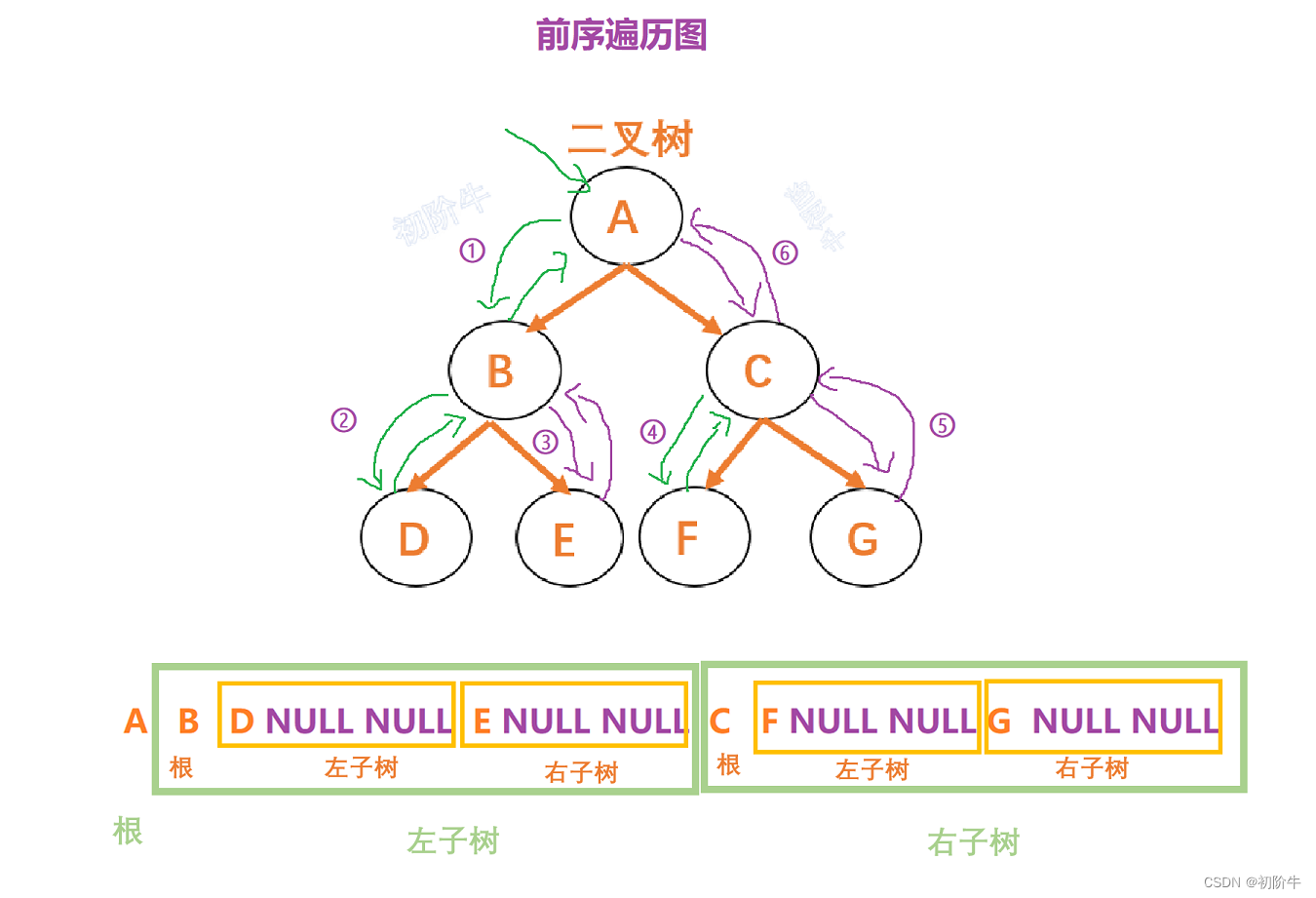
对于任意一棵二叉树,他都有由根,左子树,右子树组成.
那么就出现了三种常见的遍历二叉树的方式

前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。即:

根 ---> 左(子树) ---> 右(子树)

中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。即:

左(子树) ---> 根 ---> 右(右子树)

后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。即:

左(子树) ---> 右(子树) ---> 根

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历.

总结:

在 根 左子树 右子树三个中:

前序遍历:根节点第一个被访问.
中序遍历:根节点第中间(二个)个被访问.
后序遍历:根节点最后一个被访问.

3.1 前序遍历:

看见前序遍历,就知道根节点是第一个被访问的.即:

根 —> 左(子树) —> 右(子树)

代码递归展开图:
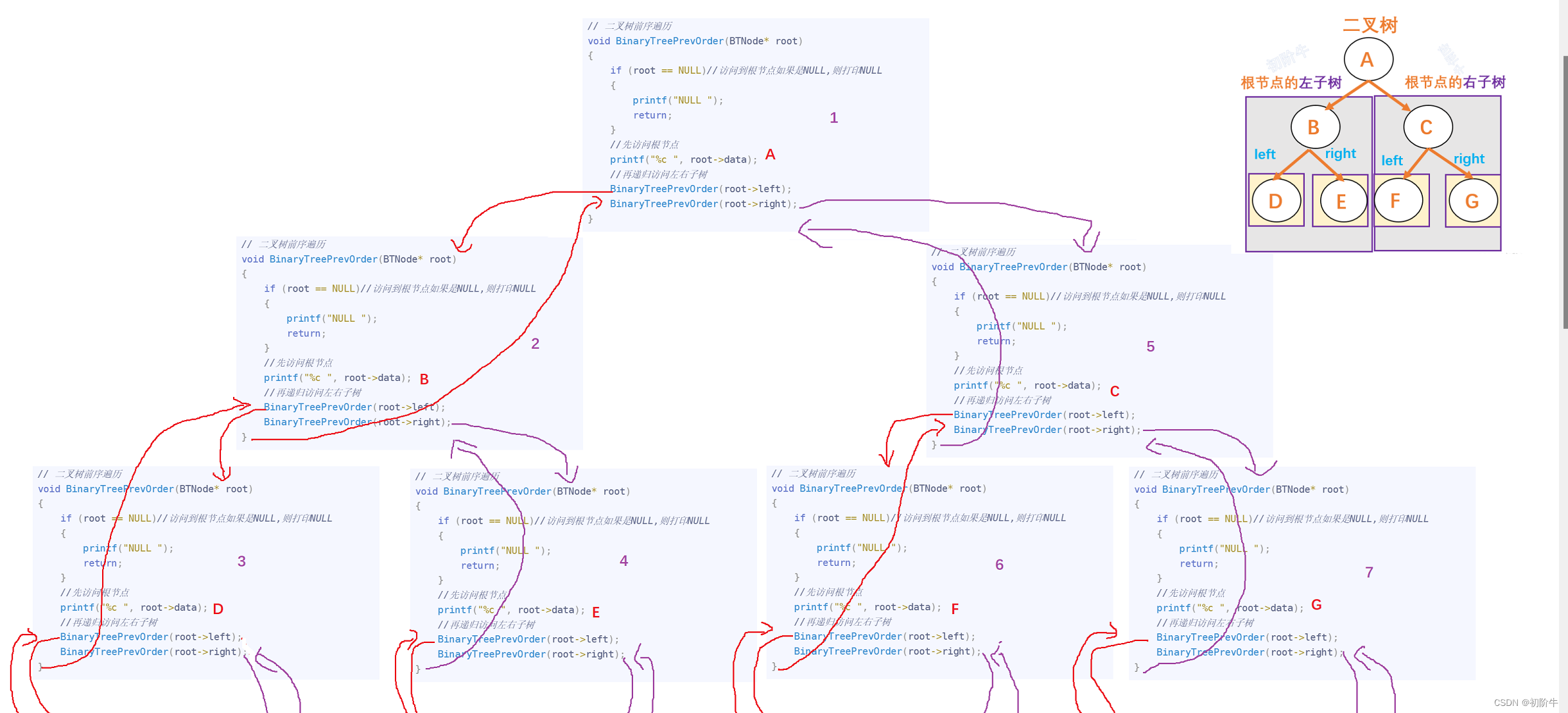
在这里插入图片描述

代码实现:

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)//访问到根节点如果是NULL,则打印NULL
	{
		printf("NULL ");
		return;
	}
	//先访问根节点
	printf("%c ", root->data);
	//再递归访问左右子树
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

3.2 中序遍历:

有了前序遍历的基础,后面两个应该好理解,如果还是不理解,可以试着画一下代码的递归展开图,帮助大家理解.

// 二叉树中序遍历 
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	//先访问左子树
	BinaryTreePrevOrder(root->left);
	//中间访问根节点
	printf("%c ", root->data);
	//最后访问右子树
	BinaryTreePrevOrder(root->right);
}

3.3 后序遍历:

// 二叉树后序遍历 
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	//先访问左右子树
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
	//最后访问根节点
	printf("%c ", root->data);
}

3.4 扩展知识:层序遍历(稍复杂)

要去按层来访问二叉树.

这里需要借助队列来实现,而且恶心的是, C语言没有队列的库函数,需要自己实现.
牛牛有关队列的博客,欢迎直接复制.
传送门

代码实现:
打印NULL版本

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);//将二叉树的根节点先入队列
	while (!QueueEmpty(&q))//只要队列非空则,继续
	{
		BTNode* tmp=QueueFront(&q);
		if (tmp)//非空结点则直接打印数据
		{
			printf("%c ", tmp->data);
		}
		else
		{
			printf("NULL ");
		}
		QueuePop(&q);//弹出根节点.将左右子树分别压入队列
		if (tmp)//只要该结点不是NULL,则将其左右子树都入队
		{
			//结点虽然非空,但是左右子树可能是NULL,所以这里NULL也进入队列了.
			QueuePush(&q, tmp->left);
			QueuePush(&q, tmp->right);
		}
	}
}

不打印NULL版本

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root) 
{
	Queue q1;
	QueueInit(&q1);
	QueuePush(&q1, root);//将根节点存入队列
	while (!QueueEmpty(&q1))
	{
		BTNode* front = QueueFront(&q1);//保存队首结点
		printf("%c ",front->data );//打印队首数据
		QueuePop(&q1);//弹出根节点
		//将刚刚弹出的结点的左右孩子入队列(所以前面要保存头结点)
		if (front->left)
			QueuePush(&q1, front->left);
		if(front->right)
			QueuePush(&q1,front->right);
	}
}

三、"二叉树"的构造(根据前序遍历)

前面都是在已经有二叉树的基础上,我们直接遍历二叉树,那二叉树怎么构建呢?

现在,我们给出要构建的二叉树的前序遍历.(#代表NULL)

BTDataType arr[50] = { "ABD##E##CF##G##" };

代码实现:

BTNode* BinaryTreeCreate(BTDataType* a,int* pi)//pi用于遍历这个数组
{
	//递归的结束条件是,当left和right都是NULL时,(左右子树都为空,则结束递归)
	if (a[*pi] == '#')//遇到NULL
	{
	//注意,即使是遇到NULL,数组也需要继续往后遍历,不然还没有构建完成
		(*pi)++;
		return NULL;
	}
	//如果不是NULL
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));//创建树结点
	//先赋值根节点
	root->data = a[(*pi)++];
	//再给左右子树赋值
	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a,pi);
	return root;
}

四、"二叉树"的销毁

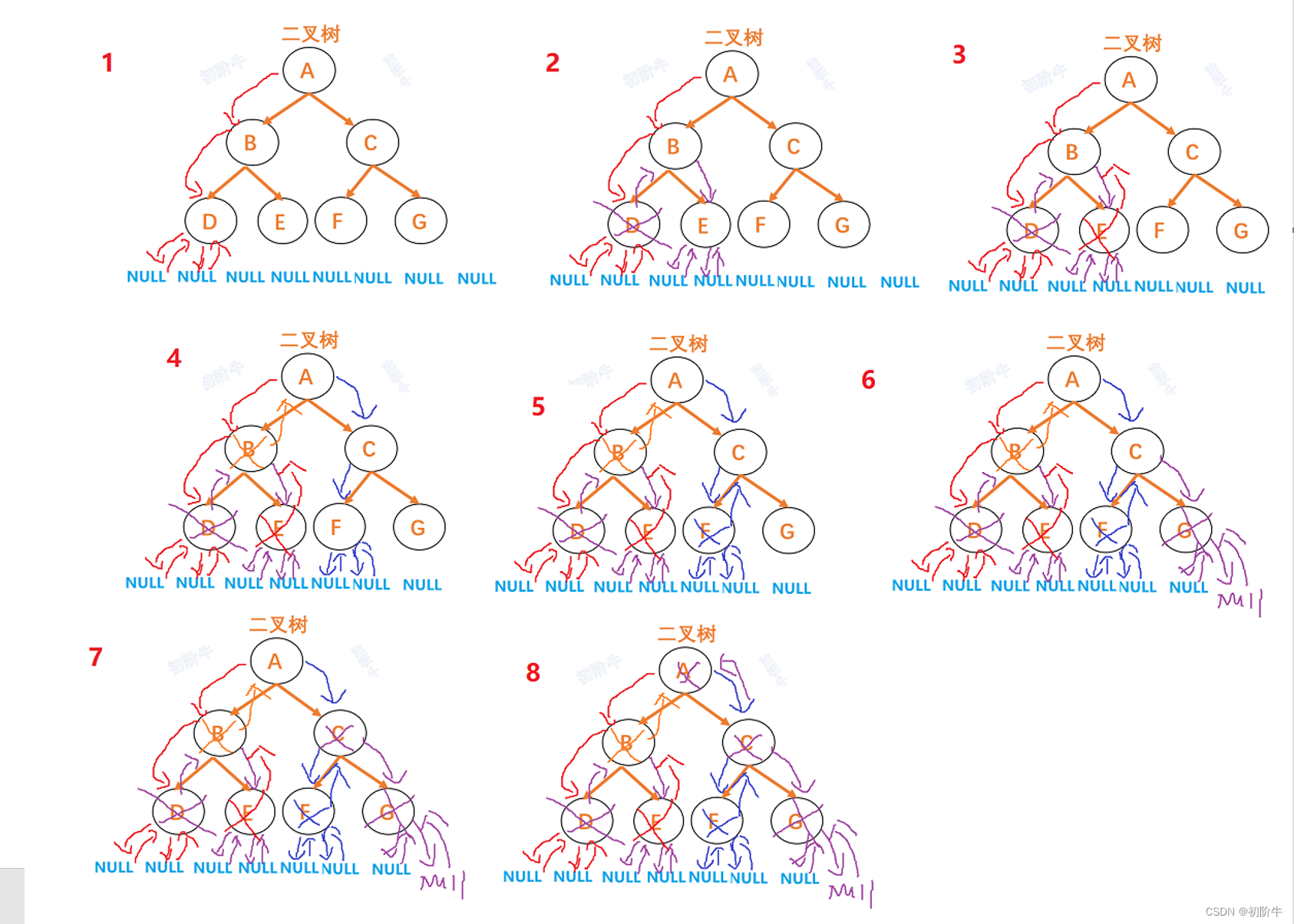
二叉树的销毁步骤:

递归访问左右子树,直到遇到NULl.访问到了最后一层.
开始释放该结点(从叶子结点开始),回退.

在这里插入图片描述

//二叉树的销毁
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)//如果走到NULL则直接返回
	{
		return;
	}
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);//这条语句一定要放在前面两条语句的后面,不然无法递归往下走.
}

五、总代码:

声明区(tree.h)

#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>

typedef char BTDataType;


typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

//根据前序遍历构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a,int* pi);

// 二叉树销毁
void BinaryTreeDestory(BTNode* root);

// 二叉树节点个数
int BinaryTreeSize(BTNode* root);

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);



//队列
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

typedef BTNode* QDatatype;

typedef struct QueueNode
{
	struct QueueNode* next;
	QDatatype data;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;
}Queue;

void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDatatype x);
void QueuePop(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);
QDatatype QueueFront(Queue* pq);
QDatatype QueueBack(Queue* pq);

队列接口实现区:(Queue.c)

#include "tree.h"
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}

void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	QNode* next = cur;
	while (next)
	{
		next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;
	pq->size = 0;
}

void QueuePush(Queue* pq, QDatatype x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	newnode->data = x;
	newnode->next = NULL;
	if (newnode == NULL)
	{
		perror("newnode malloc fail:");
		return;
	}
	//这里忘记了判断head刚开始时
	if (pq->head == NULL)//第一次插入
	{
		assert(pq->tail == NULL);
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
	pq->size++;//记住这个放后面
}
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	if (pq->head == pq->tail && pq->head == NULL)
	{
		return true;
	}
	return false;
}
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	if (pq->head->next == NULL)//代表还剩下一个结点
	{
		free(pq->head);//释放这个结点.
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	pq->size--;
}

int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}
QDatatype QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->head);
	return pq->head->data;
}

QDatatype QueueBack(Queue* pq)
{
	assert(pq);
	assert(pq->head);
	return pq->tail->data;
}

"二叉树"接口实现区:(tree.c)

#include "tree.h"

BTNode* BinaryTreeCreate(BTDataType* a,int* pi)//pi用于遍历这个数组
{
	//递归的结束条件是,当left和right都是NULL时
	if (a[*pi] == '#')//遇到NULL
	{
		(*pi)++;
		return NULL;
	}
	//如果不是NULL
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));//创建树结点
	root->data = a[(*pi)++];
	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a,pi);
	return root;
}


//二叉树的销毁
void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)//如果走到NULL则直接返回
	{
		return;
	}
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);//这条语句一定要放在前面两条语句的后面,不然无法递归往下走.
}

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}


// 二叉树中序遍历 
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	BinaryTreePrevOrder(root->left);
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->right);
}

// 二叉树后序遍历 
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
	printf("%c ", root->data);
}


// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);//将二叉树的根节点先入队列
	while (!QueueEmpty(&q))//只要队列非空则,继续
	{
		BTNode* tmp=QueueFront(&q);
		if (tmp)
		{
			printf("%c ", tmp->data);
		}
		else
		{
			printf("NULL ");
		}
		QueuePop(&q);//弹出根节点.将左右子树分别压入队列
		if (tmp)
		{
			QueuePush(&q, tmp->left);
			QueuePush(&q, tmp->right);
		}
	}
}

主测试区:(test.c)

#include "tree.h"

int main()
{
	BTDataType arr[50] = { "ABD##E##CF##G##" };
	int i = 0;
	BTNode* root = BinaryTreeCreate(arr,&i);

	//前序遍历
	printf("前序遍历:");
	BinaryTreePrevOrder(root);
	printf("\n");

	// 二叉树中序遍历 
	printf("中序遍历:");
	BinaryTreeInOrder(root);
	printf("\n");

	// 二叉树后序遍历 
	printf("后序遍历:");
	BinaryTreePostOrder(root);
	printf("\n");

	//层序遍历
	printf("二叉树的层序遍历:");
	BinaryTreeLevelOrder(root);
	printf("\n");

	//二叉树的销毁
	BinaryTreeDestory(root);
	return 0;
}