笔者自述：

一直有一个声音也一直能听到身边的大佬经常说，要把算法学习搞好，一定要重视平时的算法学习，虽然每天也在学算法，但是感觉自己一直在假装努力表面功夫骗了自己，没有规划好自己的算法学习和总结，因为后半年也该找实习了，所以每日的算法题要进行恶补，勤能补拙，因此有了这一个算法日记系列；

必读： 大佬你好，感谢您的阅读，这篇文章是我的算法笔记，方便我每日回顾；
为了不耽误您的时间，我把本篇日记的考点方向和算法知识总结列出来，如果对您有需要就继续向下进行阅读
也希望对您有帮助，和您一起通关算法！致谢

算法语言：java
题目来源：力扣–书本–初级算法，可以在力扣中搜索相关题名找到更多解法和大神方法
本文知识点：
本片文章主题搜索与回溯算法的练习， 不会的同学多写几遍，然后慢慢去理解整个过程的实现，关于三道题，主要思想是递归实现或者使用队列或者栈来进行辅助操作。

剑指 Offer 26. 树的子结构（需要多回顾）

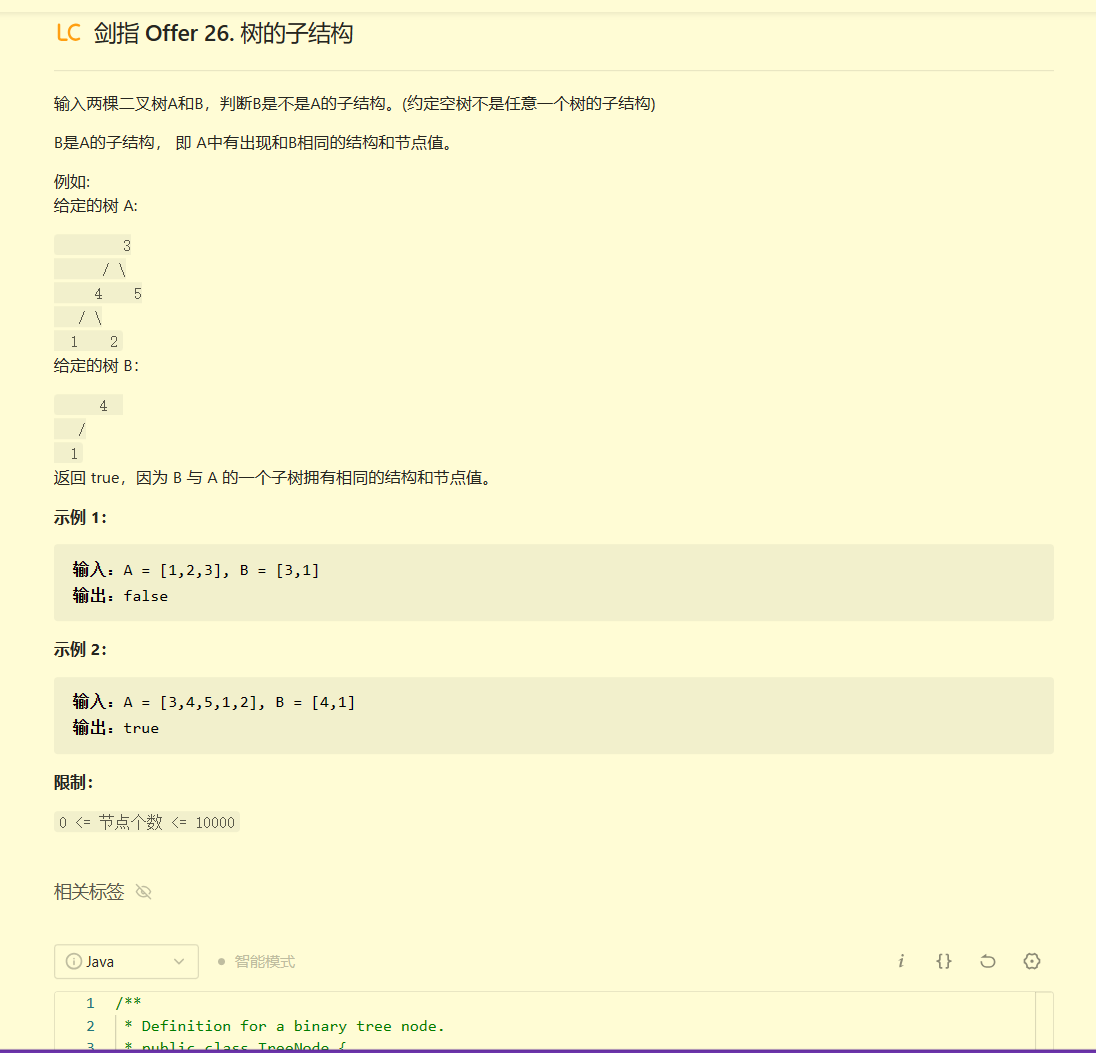
代码：

public boolean isSubStructure1(TreeNode A,TreeNode B){
        if(B == null) return false;
        return search(A,B);
    }
    public boolean compare(TreeNode A,TreeNode B){
        if( B == null) return true;
        if(A == null) return false;
        return A.val == B.val && compare(A.left,B.left) && compare(A.right,B.right);
    }
    public boolean search(TreeNode A,TreeNode B){
        if(A == null) return false;
        if(A.val == B.val && compare(A,B)) return true;
        return search(A.left,B) || search(A.right,B);
    }

学到的知识：

1. 说实话这道题我写不出来。通过分析代码可以看出，通过递归分析，从当前节点向左右子树进行判断比对，题中说明找到是子段而非子树，所以B只要满足是A的一部分就行，这道题需要多看和练习

剑指 Offer 27. 二叉树的镜像

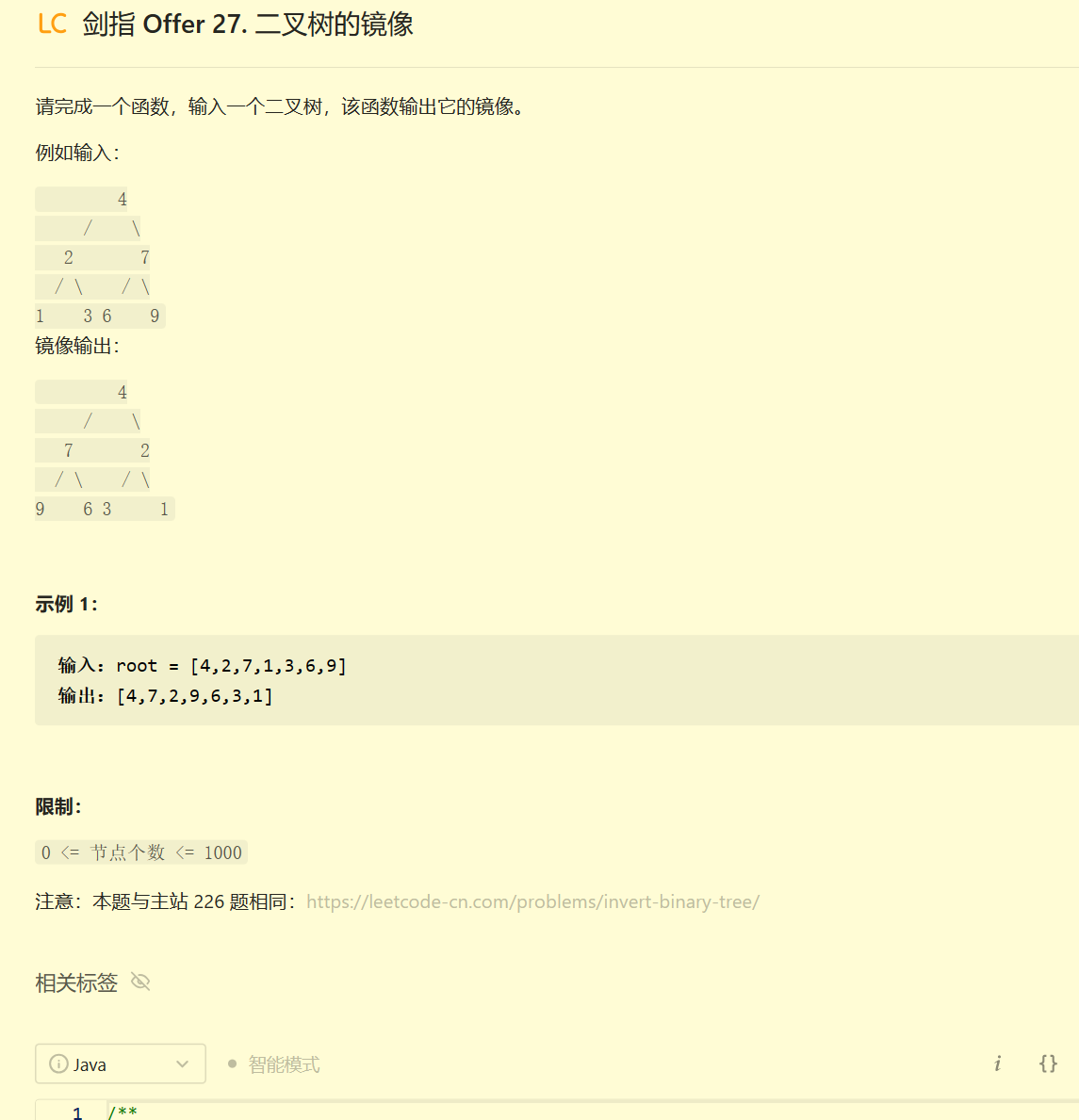
代码：

 //方法一：使用递归 ----这我是真想不出来。。
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null) return null;
        TreeNode tmp = root.left;
        root.left = mirrorTree(root.right);
        root.right = mirrorTree(tmp);
        return root;
    }
    //方法二：使用辅助栈，
    public TreeNode mirrorTree1(TreeNode root){
        if(root == null) return null;
        Stack<TreeNode> stack = new Stack<>(){{add(root);}};
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            if(node.left != null) stack.add(node.left);
            if(node.right != null) stack.add(node.right);
            TreeNode tmp = node.left;
            node.left = node.right;
            node.right = tmp;
        }
        return root;
    }

学到的知识：

1. 这道题一样，最简便的方法是使用递归，同时可以借助队列和栈来辅助操作，不过我是真想不到用递归怎么写，我想到的是使用队列实现，实现了一部分哈哈。

剑指 Offer 28. 对称的二叉树

代码：

//方法二：使用递归
    public boolean isSysmmetric1(TreeNode root){
        return root == null || dfs(root.left,root.right);
    }
    public boolean dfs(TreeNode L,TreeNode R){
        if(L == null && R == null) return  true;
        if(L == null || R == null || L.val != R.val) return false;
        return dfs(L.left,R.right) && dfs(L.right,R.left);
    }

学到的知识：

1. 递归的使用，不会的话多练习几遍，然后再去理解其中的实现过程，最后去自己实现一下。