1. 直方图、箱线图和密度图

直方图、箱线图和密度图是数据分析中十分常用的图形。它们可以帮助我们更好地理解数据的分布情况，从而更好地进行数据分析和处理。在这篇博客中，我们将介绍它们的基本原理、用途以及如何在Python中使用代码来实现。

1.1 直方图

直方图是一种常用的数据分布图，它将数据分成若干个区间，然后统计每个区间内数据的个数。通常情况下，直方图的横轴表示数据范围，纵轴表示数据出现的频数或者频率。直方图适用于连续性数据的分布情况。

下面是Python绘制直方图的代码，使用的是matplotlib库：

import matplotlib.pyplot as plt
import numpy as np

# 生成一组随机数据
data = np.random.randn(1000)

# 绘制直方图
plt.hist(data, bins=30, density=True, alpha=0.5,
         histtype='stepfilled', color='steelblue',
         edgecolor='none')
plt.title('Histogram')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

其中，np.random.randn(1000)生成了1000个标准正态分布的随机数，plt.hist()函数用于绘制直方图，bins表示将数据分成的区间数量，density表示是否对频数进行归一化，alpha表示透明度，histtype表示直方图的类型，color表示填充颜色，edgecolor表示边框颜色。最后使用plt.show()函数显示图形。

在上面的代码中，我们设置了density=True，这样直方图的纵轴就表示概率密度，而不是频数。如果需要绘制频数直方图，只需要将density设置为False即可。

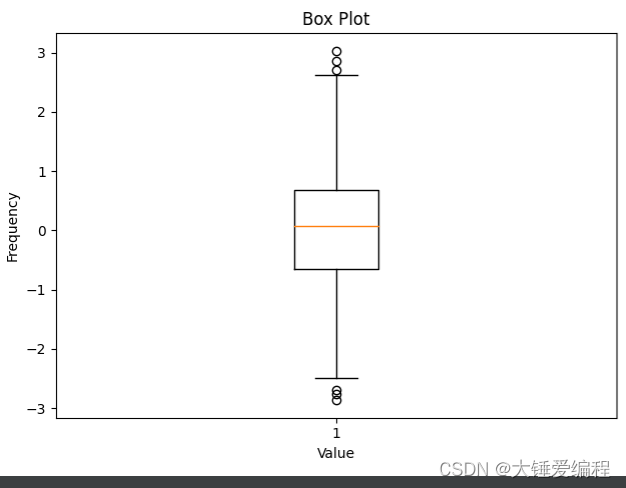
1.2 箱线图

箱线图是用于展示数据分布情况的一种图形，它由五个数值点组成：最小值、最大值、中位数、上四分位数和下四分位数。箱子的长度表示数据的四分位距，箱子内的线表示数据的中位数，箱子外的点表示离群值。箱线图适用于离散性数据的分布情况。

下面是Python绘制箱线图的代码，使用的是matplotlib库：

import matplotlib.pyplot as plt
import numpy as np

# 生成一组随机数据
data = np.random.randn(1000)

# 绘制箱线图
plt.boxplot(data, notch=False, vert=True, showfliers=True,
            labels=None, flierprops=None, medianprops=None,
            meanprops=None, whiskerprops=None, capprops=None,
            boxprops=None)

plt.title('Box Plot')
plt.xlabel('Value')
plt.ylabel('Frequency')

plt.show()

其中，data为一组随机数据，plt.boxplot()函数用于绘制箱线图，notch表示是否绘制缺口，vert表示箱线图的方向，showfliers表示是否绘制离群值，labels表示箱线图标签，flierprops表示离群值的属性，medianprops表示中位数的属性，meanprops表示均值的属性，whiskerprops表示虚线的属性，capprops表示横线的属性，boxprops表示箱体的属性。最后使用plt.show()函数显示图形。

在上面的代码中，我们设置了showfliers=True，这样箱线图中会显示离群值。如果需要隐藏离群值，只需要将showfliers设置为False即可

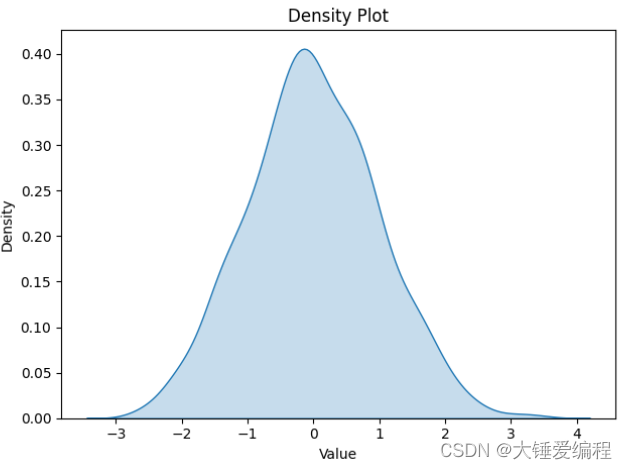
1.3 密度图

密度图是用于展示数据分布情况的一种图形，它是对直方图的一种平滑版本。它的纵轴并不是频数或频率，而是概率密度。密度图适用于连续性数据的分布情况。密度图也可以配合直方图一起绘制，以更好地理解数据的分布情况。

下面是Python绘制密度图的代码，使用的是seaborn库：

import seaborn as sns
import numpy as np

# 生成一组随机数据
data = np.random.randn(1000)

# 绘制密度图
sns.kdeplot(data, shade=True)

# 显示图形
plt.title('Density Plot')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()

其中，data为一组随机数据，sns.kdeplot()函数用于绘制密度图，shade表示是否填充颜色。最后使用plt.show()函数显示图形。

密度图的优点是可以更准确地表达数据分布情况，而不会受到分组的影响。同时，使用密度图可以更好地理解数据分布的形状，例如是否对称、是否有峰值等等。

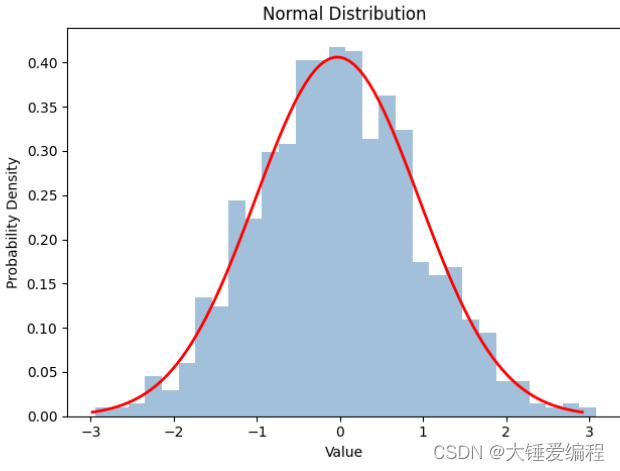
2. 正态分布

正态分布是一种常见的概率分布。在实际的数据分析中，很多数据都符合正态分布。因此，理解正态分布的基本原理和性质对于数据分析非常重要。在这篇博客中，我们将介绍正态分布的基本概念、性质和应用，并且使用Python代码来生成和可视化正态分布。

下面是Python绘制正态分布图的代码，使用的是matplotlib库：

import matplotlib.pyplot as plt
import numpy as np

# 生成一组符合标准正态分布的随机数据
data = np.random.randn(1000)

# 绘制正态分布图
plt.hist(data, bins=30, density=True, alpha=0.5,
         histtype='stepfilled', color='steelblue',
         edgecolor='none')

# 绘制正态分布曲线
mu, sigma = data.mean(), data.std()
x = np.linspace(mu - 3 * sigma, mu + 3 * sigma, 100)
plt.plot(x, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp(- (x - mu)**2 / (2 * sigma**2)),
         linewidth=2, color='r')
plt.title('Normal Distribution')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.show()

其中，np.random.randn(1000)生成了1000个标准正态分布的随机数，使用plt.hist()函数绘制数据的直方图，bins表示将数据分成的区间数量，density表示是否对频数进行归一化，alpha表示透明度，histtype表示直方图的类型，color表示填充颜色，edgecolor表示边框颜色。使用plt.plot()函数绘制正态分布曲线，mu和sigma分别表示数据的均值和标准差，x为一组等间隔的数值，1/(sigma * np.sqrt(2 * np.pi)) * np.exp(- (x - mu)**2 / (2 * sigma**2))表示标准正态分布的概率密度函数。最后使用plt.show()函数显示图形。

在上面的代码中，我们将正态分布曲线绘制在了直方图上方，这样可以更好地描述数据分布的形态。

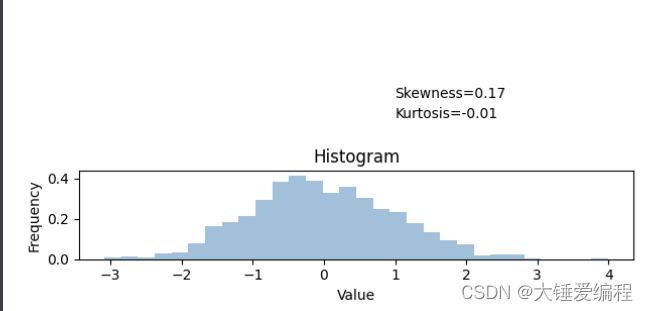
3. 偏度和峰度

偏度和峰度是用于描述数据分布形态的两个重要指标。通过偏度和峰度的计算，我们可以更准确地描述数据的分布情况，从而更好地进行数据分析。在这篇博客中，我们将介绍偏度和峰度的概念、计算方法和应用，并且使用Python代码来计算和可视化偏度和峰度。

偏度和峰度是用于描述数据分布形态的两个重要指标。偏度描述的是数据分布的不对称程度，通常用于判断数据分布是否为正态分布。如果偏度为0，则数据分布为对称分布；如果偏度大于0，则数据分布右偏；如果偏度小于0，则数据分布左偏。峰度描述的是数据分布的峰态，即分布的陡峭程度。峰度为0表示正态分布，峰度大于0表示分布比正态分布更陡峭，峰度小于0表示分布比正态分布更平缓。

import numpy as np
from scipy.stats import kurtosis, skew
import matplotlib.pyplot as plt

# 生成一组随机数据
data = np.random.randn(1000)

# 计算偏度和峰度
sk = skew(data)
ku = kurtosis(data)

# 绘制直方图
plt.hist(data, bins=30, density=True, alpha=0.5,
         histtype='stepfilled', color='steelblue',
         edgecolor='none')
plt.title('Histogram')
plt.xlabel('Value')
plt.ylabel('Frequency')

plt.text(1, 0.8, 'Skewness={:.2f}'.format(sk))
plt.text(1, 0.7, 'Kurtosis={:.2f}'.format(ku))

plt.show()

其中，skew(data)和kurtosis(data)函数分别用于计算数据的偏度和峰度。最后使用plt.text()函数在图形上方添加偏度和峰度的数值。

在上面的代码中，我们使用了scipy库中的kurtosis和skew函数来计算偏度和峰度。如果需要计算样本的偏度和峰度，可以使用bias=False参数。

通过偏度和峰度的计算，我们可以更准确地描述数据的分布情况，从而更好地进行数据分析。