微分方程（Differential equation）是描述自然现象中变量之间关系的数学语言。它是以函数、导数、微分等数学概念为基础的方程，揭示了自然现象中变量之间的内在联系。微分方程在物理学、工程学、生物学、经济学、统计学等各领域都有广泛的应用。

微分方程可以分为一阶微分方程和高阶微分方程两类。一阶微分方程包括变量的一阶导数，而高阶微分方程则包括变量的高阶导数。根据微分方程的特征，可以采用不同的方法来求解。

解微分方程的一些基本方法包括：

1. 变量分离法：把微分方程变成两个变量的函数，然后分别对它们进行积分。

2. 齐次微分方程法：针对某一类形式的微分方程，寻找一种特殊的代换方法，使得该方程变为可分离变量的形式。

3. 一阶线性微分方程法：将微分方程化为一阶线性微分方程，然后应用线性微分方程的解法。

4. 常系数线性微分方程法：针对一类特殊形式的一阶/二阶微分方程，寻找与方程可能成的三种解的线性组合的通解。

5. 动力学法：将微分方程化为动力学系统，通过数值模拟等方法研究微分方程的行为和稳定性。

微分方程的应用非常广泛，例如：

1. 在物理学中，微分方程可以用来描述物理规律，例如运动学、力学、热力学、量子力学等领域。

2. 在工程学中，微分方程可以用来解决控制问题、电路分析、弹性力学等问题。

3. 在生物学中，微分方程可以用来研究生物进化、人口增长、生物遗传等问题。

4. 在金融学中，微分方程可以用来描述股票价格变化、期权定价、风险管理等问题。

因此，微分方程是自然科学和社会科学研究中不可或缺的数学基础。

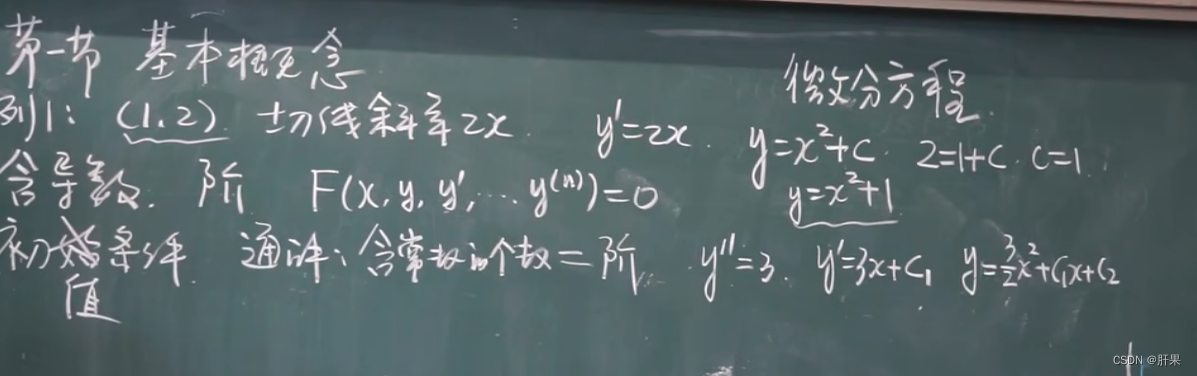
可分离变量

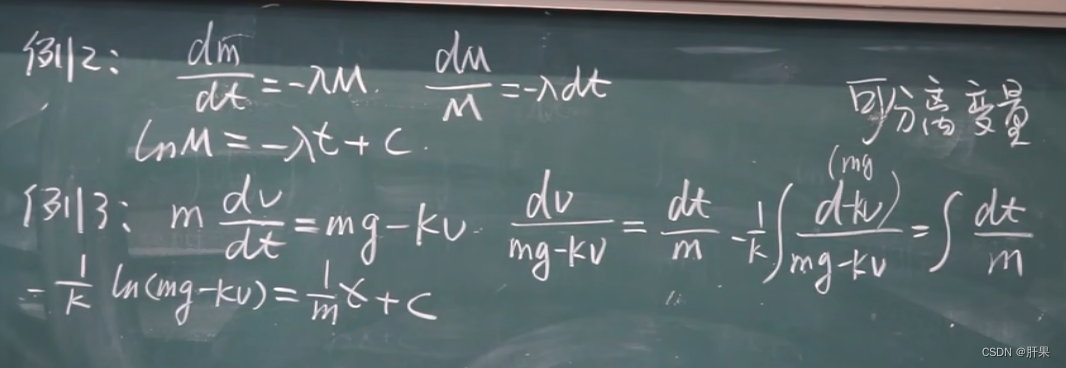
齐次方程

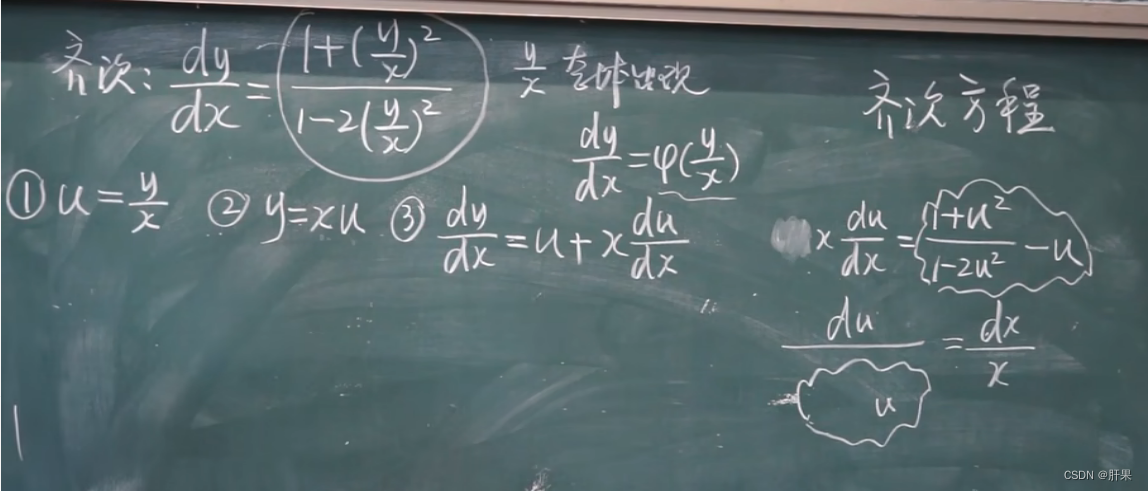
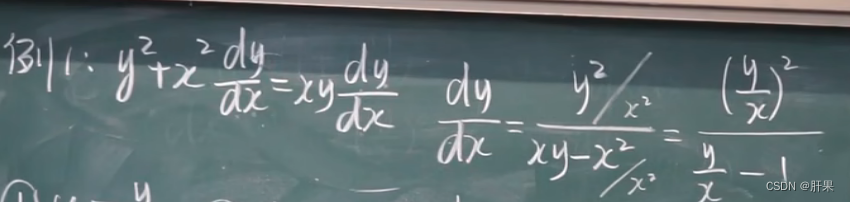
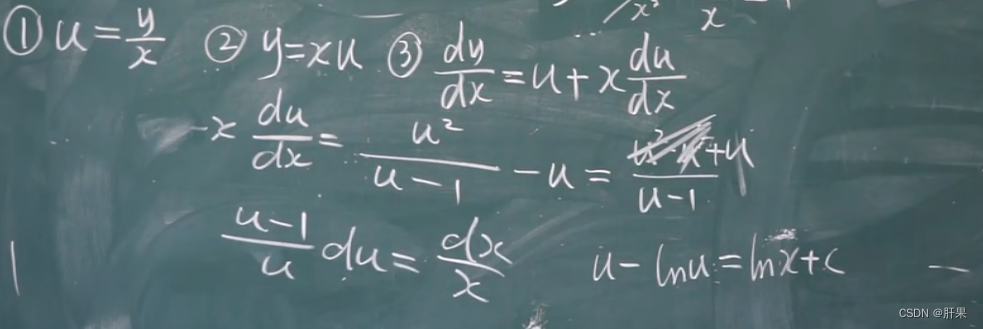
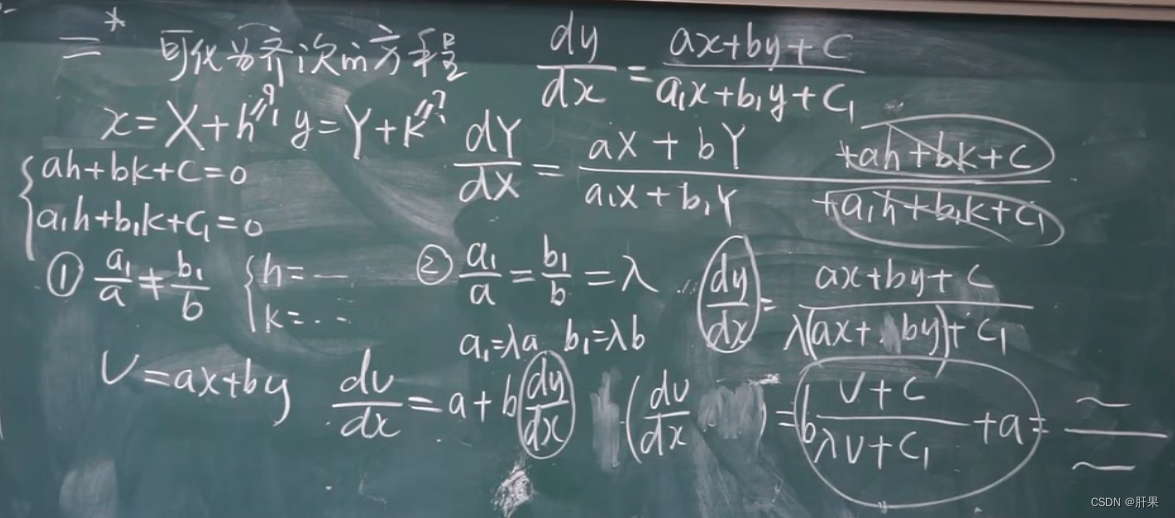
一阶线性微分方程

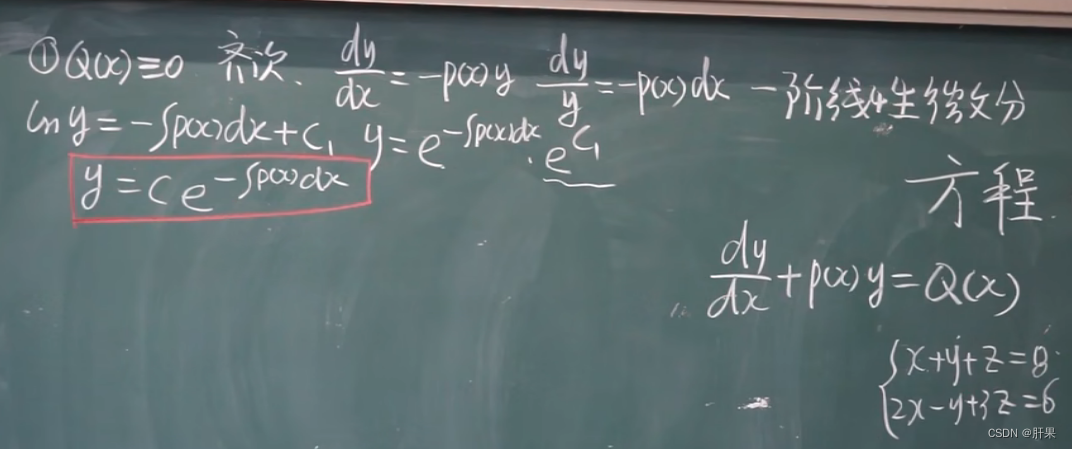
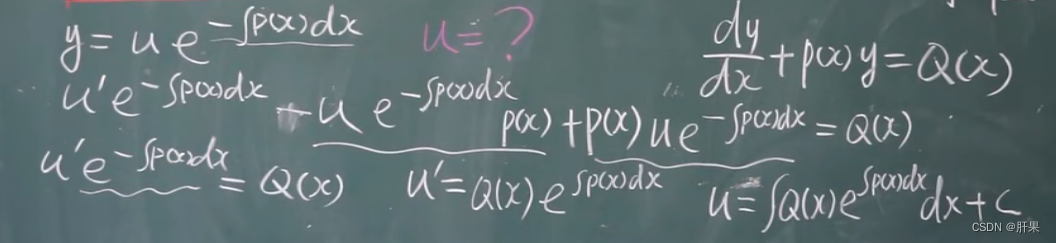
重点记忆

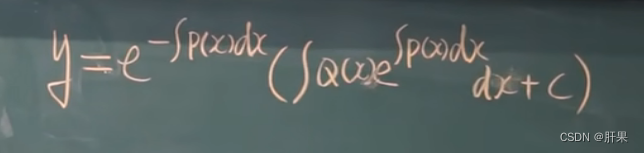
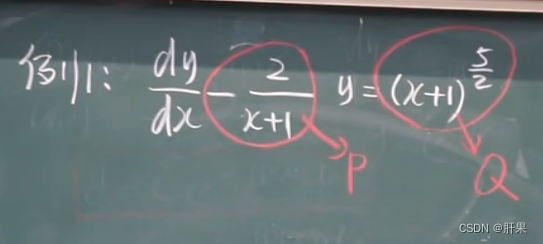
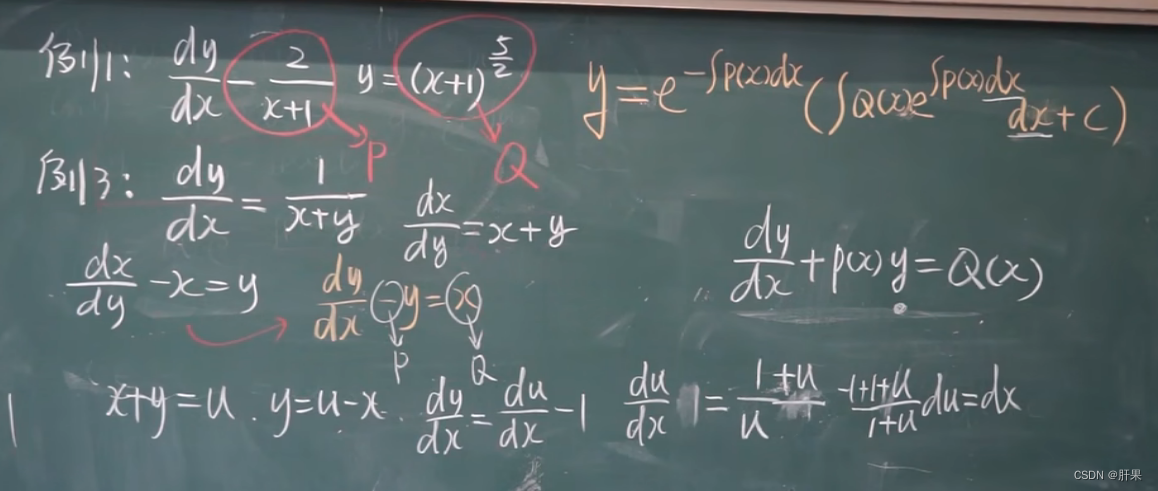
伯努利方程

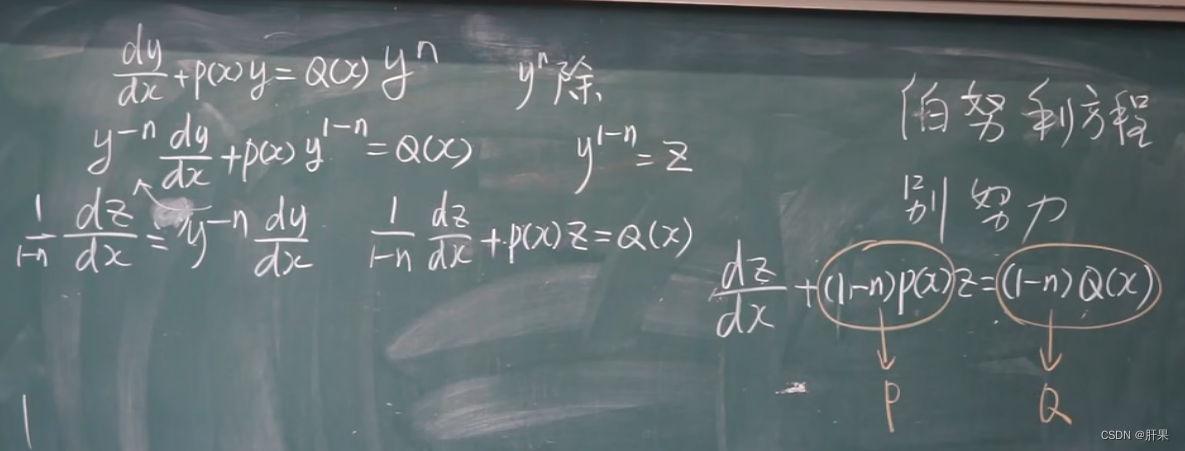
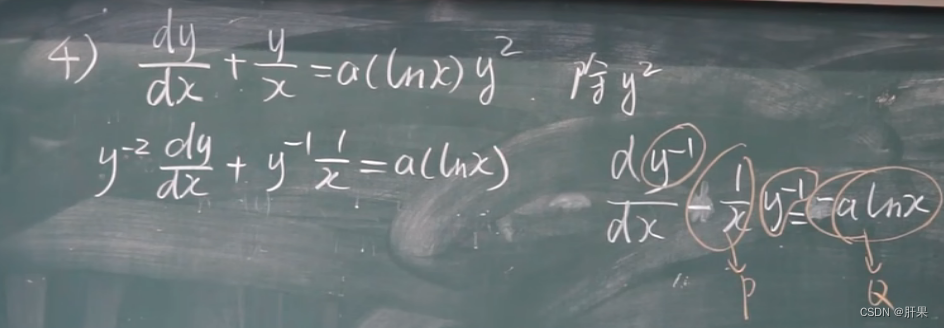
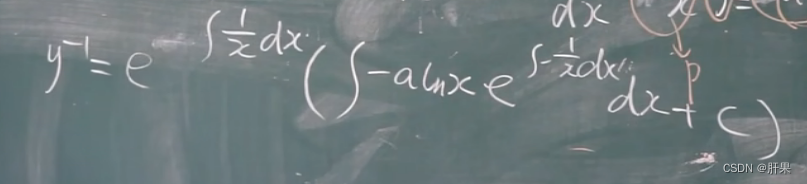
可降阶的高阶微分方程

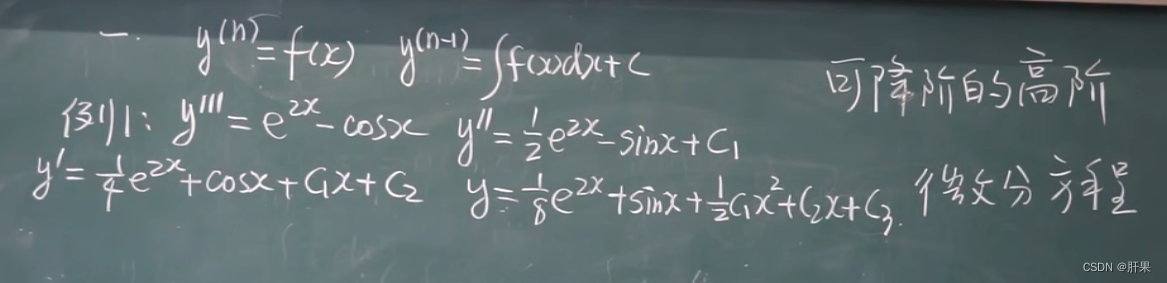
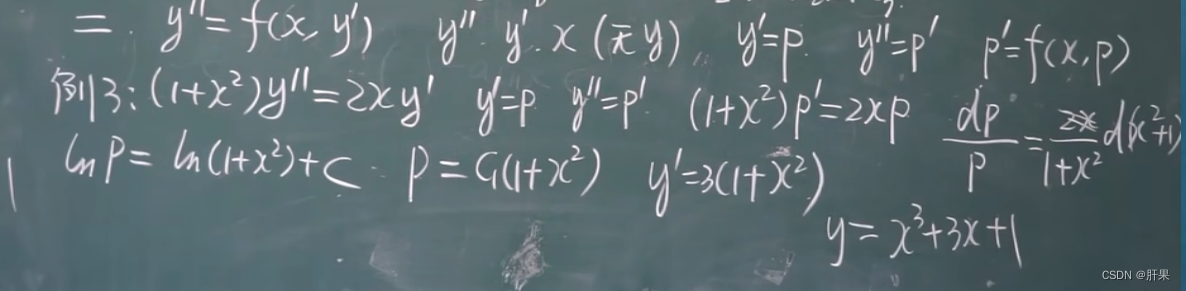
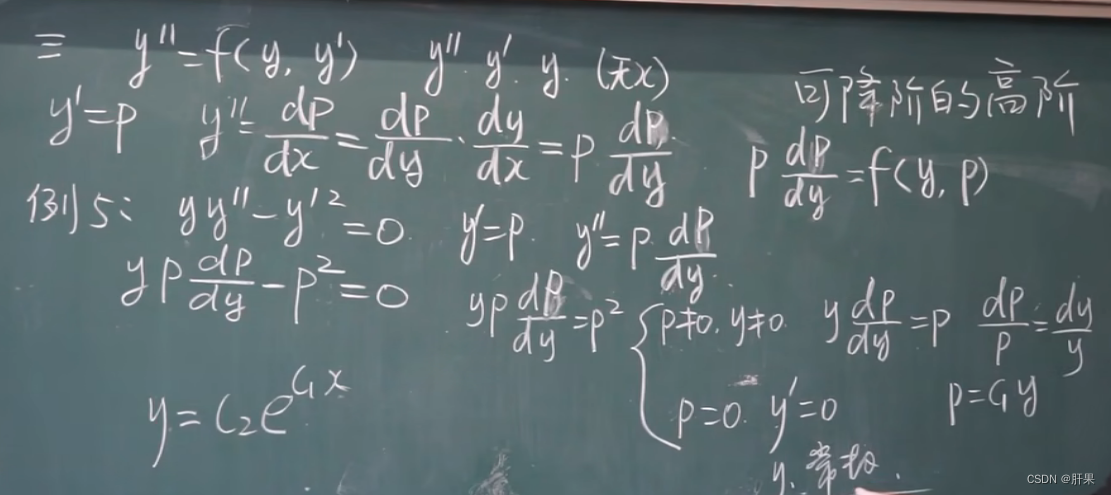
常系数齐次线性微分方程

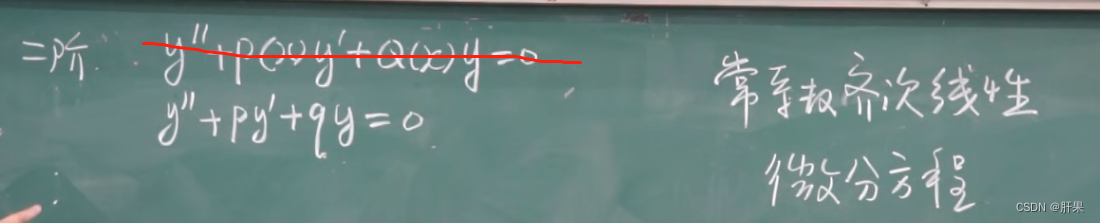
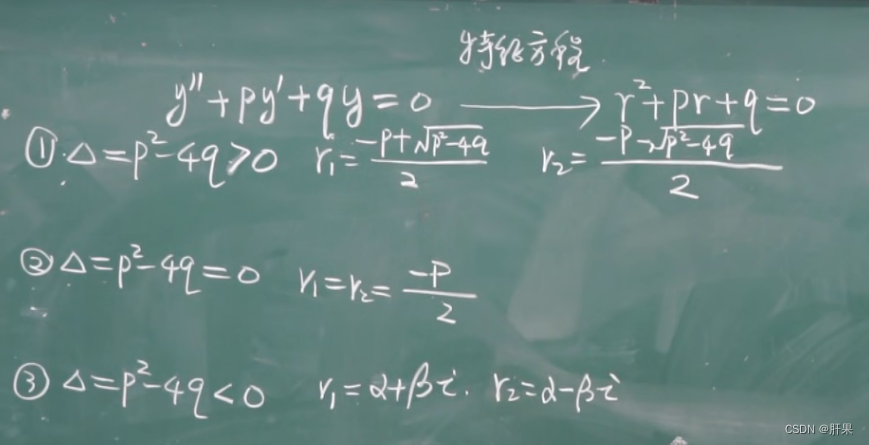
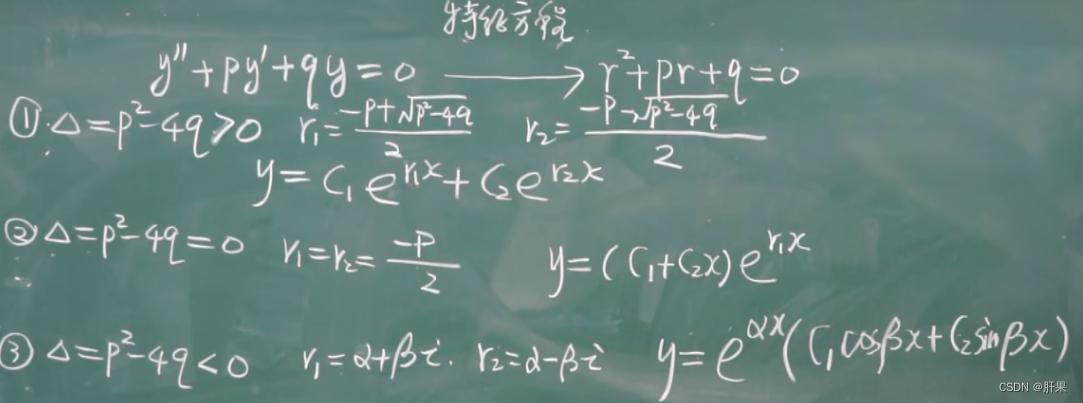
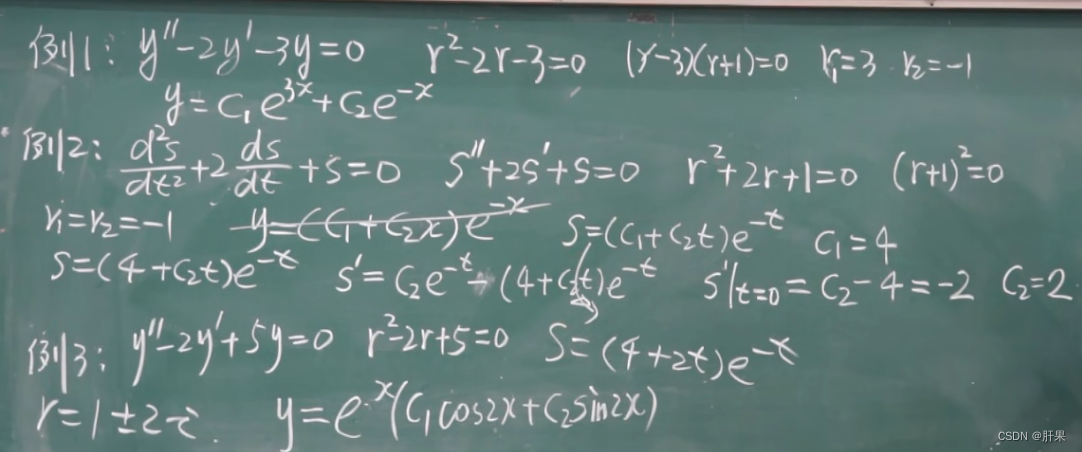
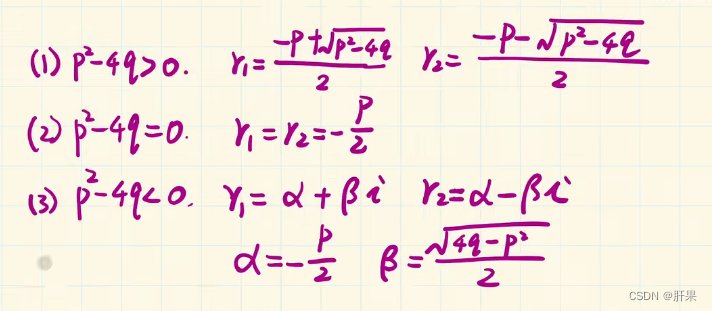
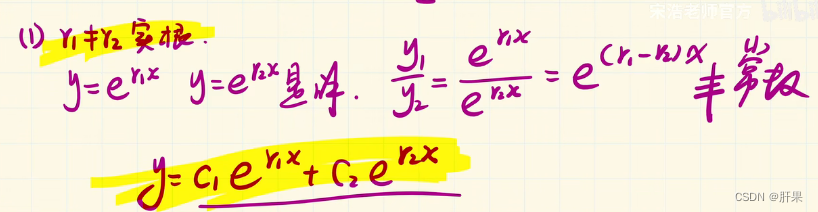
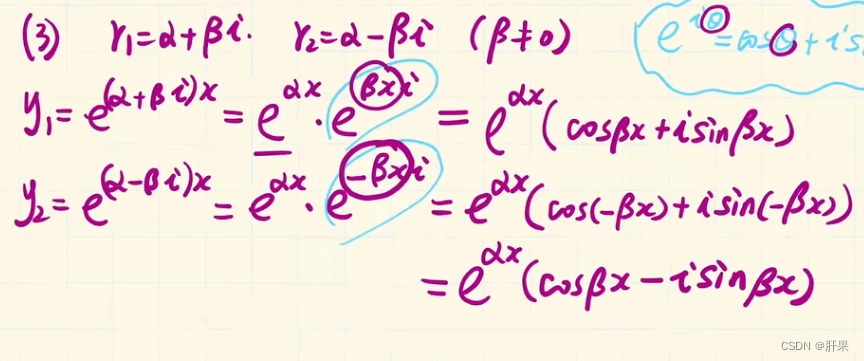
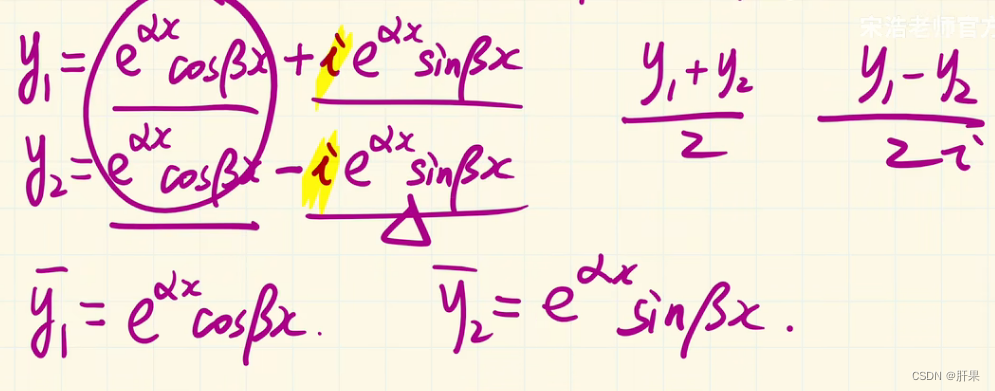
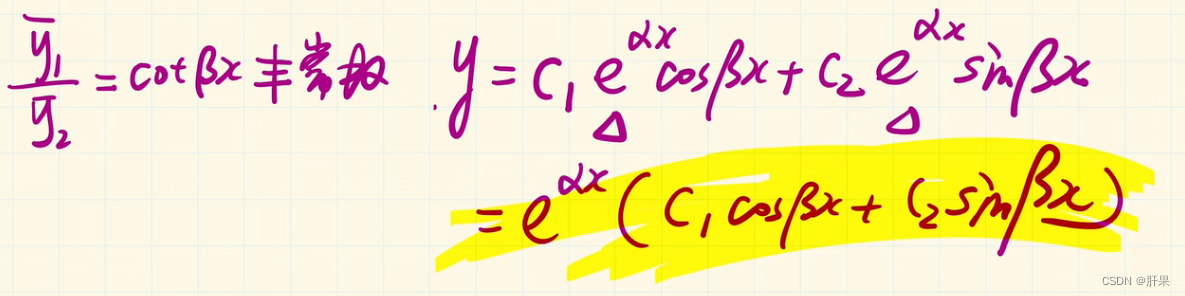
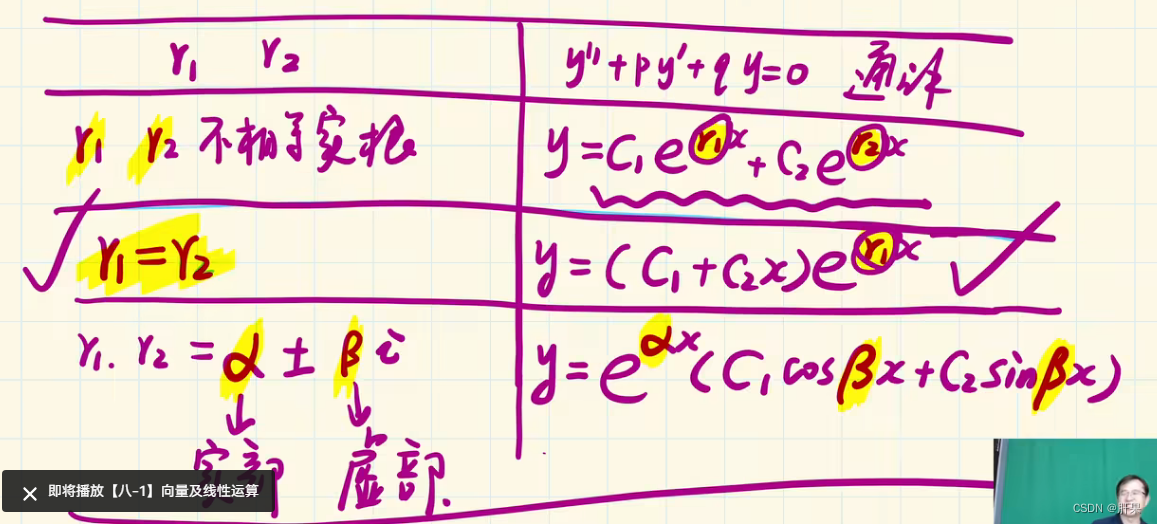
到此为止，高数上的内容完结。但是时间已经过去二周。这样下去，等到学习玩所有高等数学、线性代数、概率论和离散数学不知何时了。
因此决定从后面开始，数学基础和C++同步进行。