原理:
Dijkstra算法是解决**单源最短路径**问题的**贪心算法**
它先求出长度最短的一条路径,再参照该最短路径求出长度次短的一条路径
直到求出从源点到其他各个顶点的最短路径。
首先假定源点为u,顶点集合V被划分为两部分:集合 S 和 V-S。 初始时S中仅含有源点u,其中S中的顶点到源点的最短路径已经确定。
集合S 和V-S中所包含的顶点到源点的最短路径的长度待定,称从源点出发只经过S中的点到达V-S中的点的路径为特殊路径,
并用dist[]记录当前每个顶点对应的最短特殊路径长度。
选择特殊路径长度最短的路径,将其连接的V-S中的顶点加入到集合S中,同时更新数组dist[]。一旦S包含了所有顶点,dist[]就是从源到所有其他顶点的最短路径长度。
(1)数据结构。 设置地图的带权邻接矩阵为map[][],即如果从源点u到顶点i有边,就令map[u][i]=<u,i>的权值,否则map[u][i]=∞;
采用一维数组dist[i]来记录从源点到i顶点的最短路径长度:采用一维数组p[i]来记录最短路径上i顶点的前驱。
(2)初始化。令集合S={u},对于集合V-S中的所有顶点x,初始化dist[i]=map[u][i],如果源点u到顶点i有边相连,初始化p[i]=u(i的前驱是u),否则p[i]=-1
(3)找最小。在集合V-S中依照贪心策略来寻找使得dist[j]具有最小值的顶点t,即dist[t]=min,则顶点t就是集合V-S中距离源点u最近的顶点。
(4)加入S战队。将顶点t加入集合S,同时更新V-S
(5)判结束。如果集合V-S为空,算法结束,否则转6
(6)借东风。在(3)中已近找到了源点到t的最短路径,那么对集合V-S中所有与顶点t相邻的顶点j,都可以借助t走捷径。
如果dist[j]>dist[t]+map[t][j],则dist[j]=dist[t]+map[t][j],记录顶点j的前驱为t,p[j]=t,转(3)。
//我自己在这里理解就是,从u找到与它最近的点t,在从t找到与它最近的点j,在....按照这样持续下去,直到最后一个点
这里我再通俗的解释下这个借东风的意思。
源点为1,如果我们找到了距离源点最近的点2,且点2与3,4相连。
这样,我们如果要倒3,4有两种方法:
1->2->3(4)
1->3(4)
这里我们就要判断是从1直接到3(4)快,还是经过2后快。假设<1,2>=2 / <2,3>=3 / <1,3>=4
根据上面的数据,我们第一次找最小找到的是2结点,如果我们直接把2替换掉1当做源点继续找下一个最近的点,这种方法是错的。
因为可以看出1->3只用4,而过2的话要用5。
实现代码如下:
#include<bits/stdc++.h>
using namespace std;//1899 20296
const int N=2000; //城市个数可修改
const int INF=1e7; //初始化无穷大为.......
int G[N][N],dist[N],p[N],n,m; //n为城市个数,m为城市间路线的条数
bool flag[N]; //如果flag[i]=true,说明该顶点i已经加入到集合S;否则i属于集合V-S
void Dijkstra(int u){
for(int i=1;i<=n;i++){//********>>>--1--<<<******//
dist[i]=G[u][i]; //初始化源点u到其他各个顶点的最短路径长度
flag[i]=false;
if(dist[i]==INF)
p[i]=-1; //说明源点u到顶点i无边相连,设置p[i]=-1
else
p[i]=u; //说明源点u到顶点i有边相连,设置p[i]=u
}
flag[u]=true;//初始化集合S中,只有一个元素:源点u
dist[u]=0; //初始化源点u的最短路径为0,自己到自己的最短路径
for(int i=1;i<=n;i++){//********>>>--2--<<<******//
int temp=INF,t=u;
for(int j=1;j<=n;j++){//>>--3--<<在集合V-S中寻找距离源点u最近的顶点t
if(!flag[j] && dist[j]<temp){
t=j; //记录距离源点u最近的顶点
temp=dist[j];
}
}
if(t==u) return ; //找不到t跳出循环
flag[t]=true; //否则,将t加入集合S
for(int j=1;j<=n;j++){//>>--4--<<更新集合V-S中与t邻接的顶点到u的距离
if(!flag[j] && G[t][j]<INF){//!flag[j]表示j在v-s集合中,map[t][j]<INF表示t与j邻接
if(dist[j]>(dist[t]+G[t][j])){//经过t到达j的路径更短
dist[j]=dist[t]+G[t][j];
p[j]=t; //记录j的前驱为t
}
}
}
}
}
void findpath(int u)
{
int x;
stack<int>s;
cout << "源点为:" << u << endl;
for (int i = 1; i <= n; i++)
{
x = p[i];
while (x != -1)
{
s.push(x);
x = p[x];
}
cout << "源点到其他各顶点的最短路径为:";
while (!s.empty())
{
cout << s.top() << "--";
s.pop();
}
cout << i << ";最短距离为:" << dist[i] << endl;
}
}
int main(){
int u, v, w, st;
ifstream fin("input.txt");
fin >> n >> m;
for(int i=1;i<=n;i++)//初始化图的邻接矩阵
for (int j = 1; j <= n; j++)
{
G[i][j] = INF;//初始化邻接矩阵为无穷大
}
while(fin>>u >> v >> w)
{
G[u][v] = min(G[u][v], w); //邻接矩阵存储,保留最小的距离
}
cout << "请输所在的位置:" << endl;
cin>>st;
Dijkstra(st);
findpath(st);
return 0;
}
运行结果:

注意距离为10000000表示不可达。
数据如下:第一行为节点个数,第二行为边数,后面的为有向边和权重
数据集下载连接:
链接:https://pan.baidu.com/s/16JUotOET7pRHcRG6lUexKg?pwd=k3v2
提取码:k3v2
数据长这样:
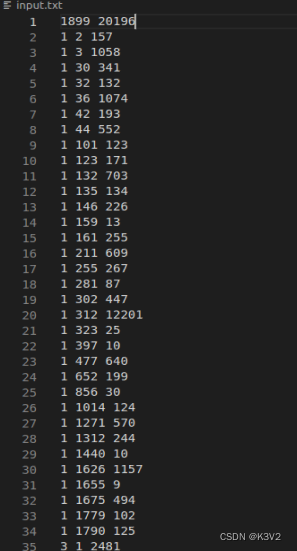
也可以用这一组数据来测试:
6 9
0 1 7
0 2 9
0 5 14
1 2 10
1 3 15
2 3 11
2 5 2
3 4 6
4 5 9