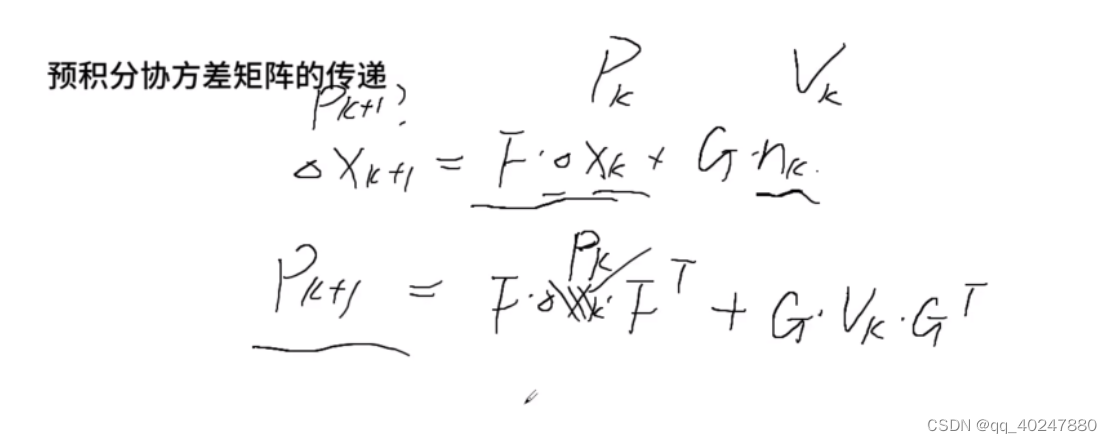
OpenCV去畸变undistortPoints原理解析

不动点迭代法—单变量非线性方程近似根matlab求解

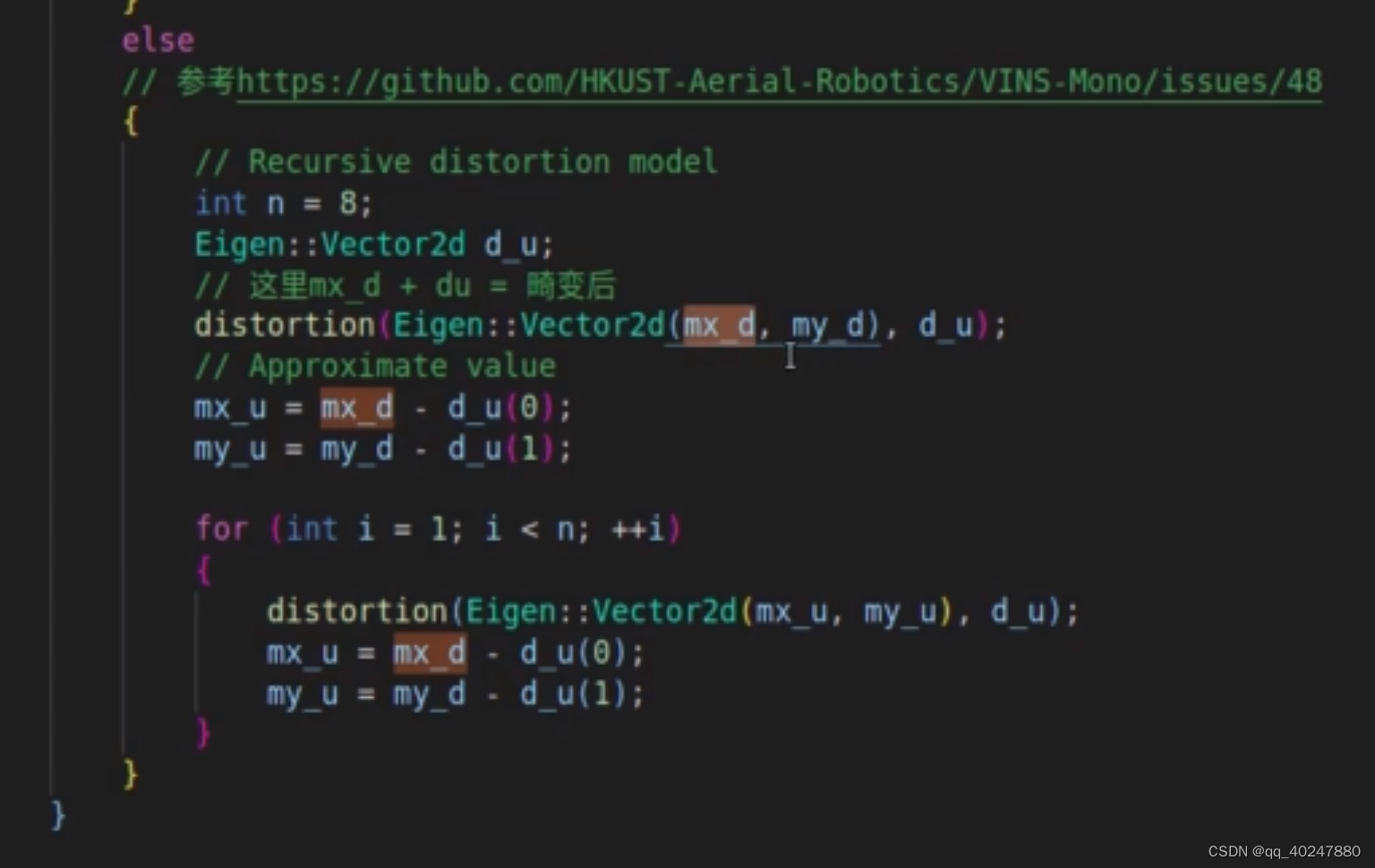
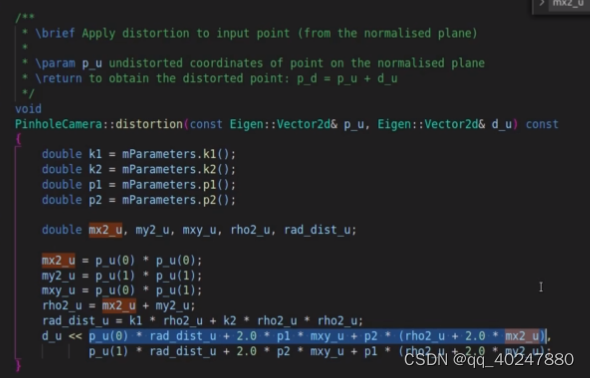
淦VINS-MONO源码 03–openCV与VINS中去畸变方法的不同

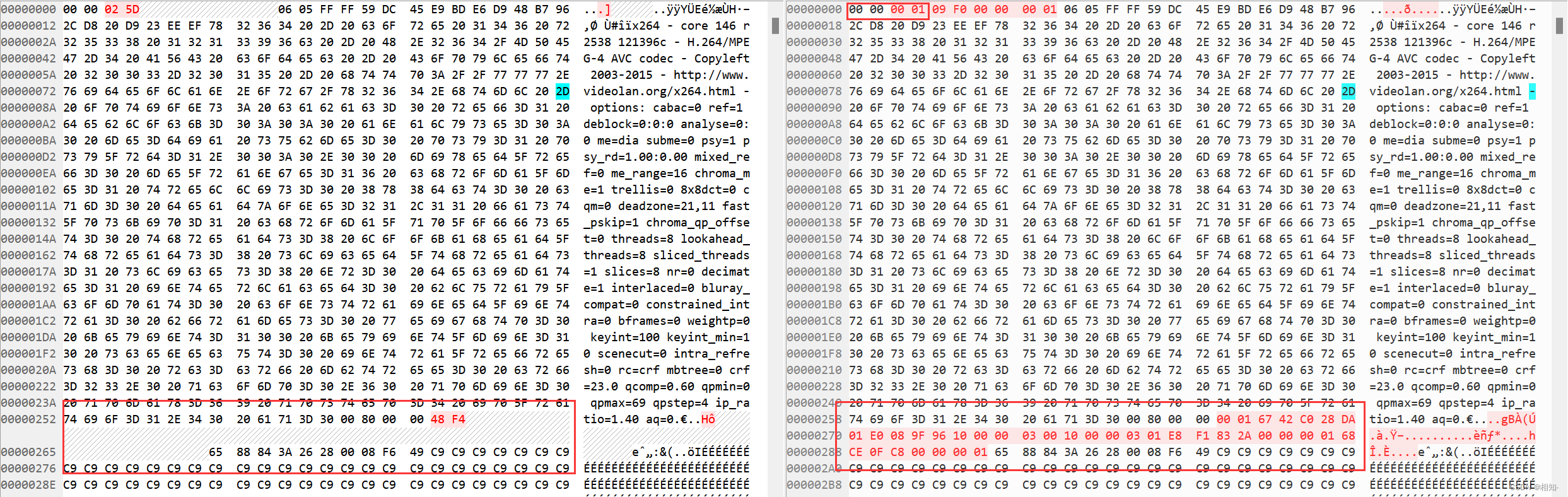
这里用的方法和openCV不同，假设现在求A点的去畸变坐标，那么我们将A的坐标直接代入畸变模型中，求得再次畸变的坐标，并求得这个坐标和A之间的距离d.因为越靠近中心这个d越小，此时肯定小于真实坐标到A的距离dt。所以我们在朝真实畸变方向(再次畸变的反方向)上加上这个d，得到一个靠近真实值的方向，在以这个点再进行一次畸变求得距离d2，d2肯定大于d小于dt。d2在加到坐标A上 得到更靠近的结果，代码中一共进行了8次迭代。这种方法比openCV中的方法快了不少。

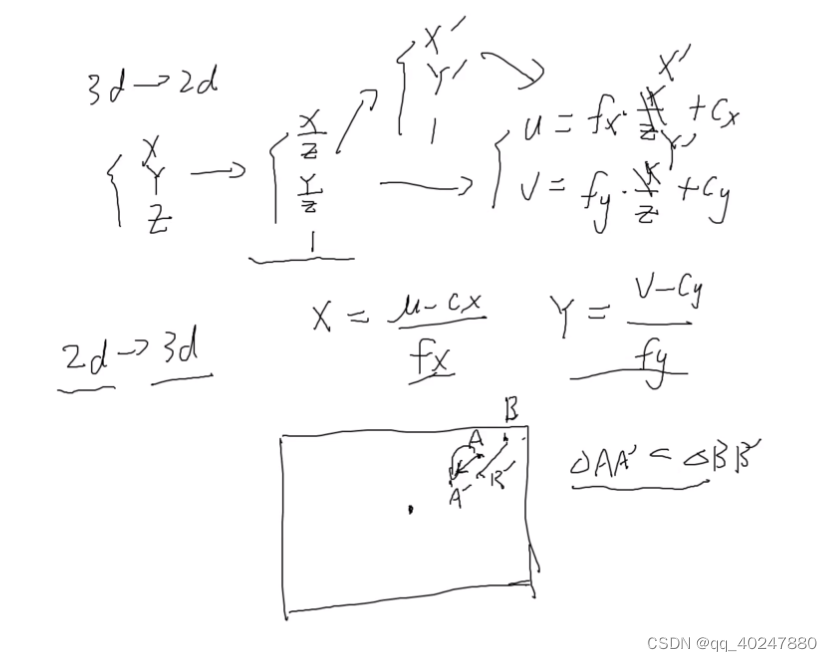
针孔相机投影模型

第三章imu预积分

旋转矩阵约束
作者：jh h
链接：https://www.zhihu.com/question/386629150/answer/1752898777
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

(已修改)旋转矩阵的9个参数，存在6个约束条件，所以只有3个自由度：三个向量的模长为1这3个条件、三个向量两两垂直2个条件（XY垂直，XZ垂直这两个）、以及右手系（或左手系）这1个条件（这个条件意味着行列式是1或-1，也暗示了如果XY垂直YZ垂直，则XZ也会垂直）。9 - 3 - 2 - 1 = 3类似的，四维空间的旋转矩阵16个参数，存在10个约束条件，有6个自由度：四个向量模长为1这4个条件、四个向量互相垂直5个条件（XY、XZ、XW、YZ、YW，以及自动得到的ZW）、坐标系手性1个条件（单位矩阵中，有奇数个还是偶数个1变成了-1，只有这两种手性）。 16 - 5 - 4 - 1 = 6nnn 维空间的旋转矩阵 n2n^{2}n{2} 个参数的情况：模长为1的条件，约束条件数量为 nnn 向量相互垂直的条件，约束条件数量为 [n(n−1)/2−1][ n(n-1)/2 -1 ][ n(n-1)/2 -1 ] 坐标系手性的条件，约束条件数量为 1自由度 = n2−n−[n(n−1)/2−1]−1=n(n−1)/2n^{2} - n - [ n(n-1)/2 -1 ] - 1= n(n-1)/2n^{2} - n - [ n(n-1)/2 -1 ] - 1= n(n-1)/2 ps: n维空间的(旋转+平动)恰好能够一一映射到(n+1)维空间的纯旋转。一个例子是，闵可夫斯基空间把三维空间的平动部分（洛伦兹收缩）映射到了所谓四维"时空"的X-T、Y-T、Z-T轴的旋转上面，同时三维旋转部分不变。洛伦兹收缩是一个客观现象，但是四维"时空"只是一个人们主观提出的一个数学模型，数学意义和物理意义需要分开。

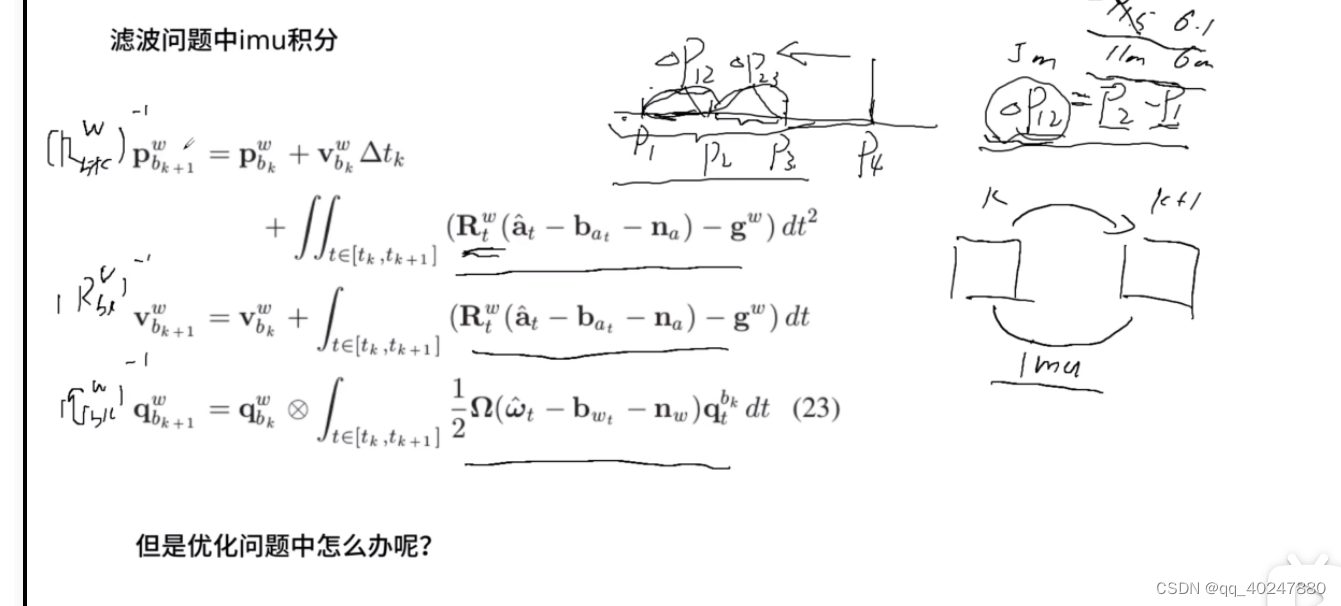
左右两边都乘以Rwbk的逆，去掉他的影响。左边就是两帧之间的约束，右边是不含w到bk变化的表达式。卡尔曼滤波预测是第推imu，更新是观测cam

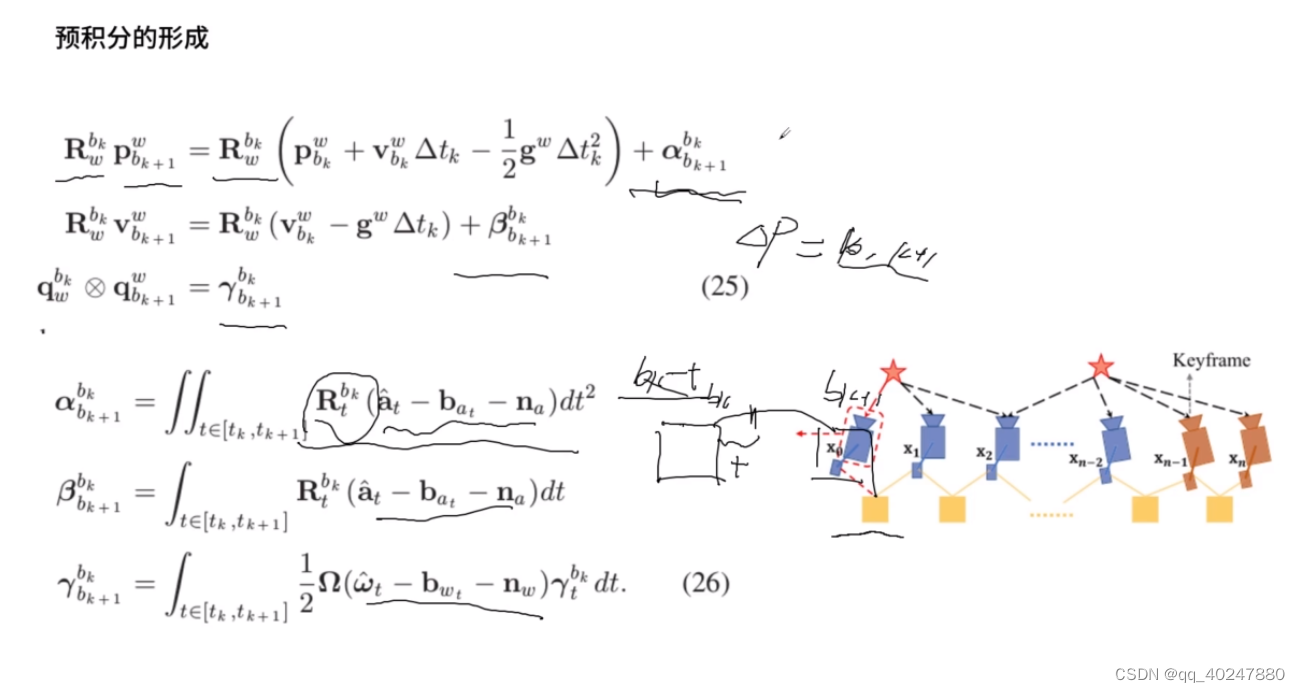
上面是连续时间，下面是离散时间,对应代码midPointIntegration，alpha，beta都是delta对应的量

迭代中，delta x一直都是0，因为输出的总是自己认为的最优值，但是deltax的协方差会变大，经过卡尔曼滤波后结合观测deltay的方差，deltax的方差会下降。

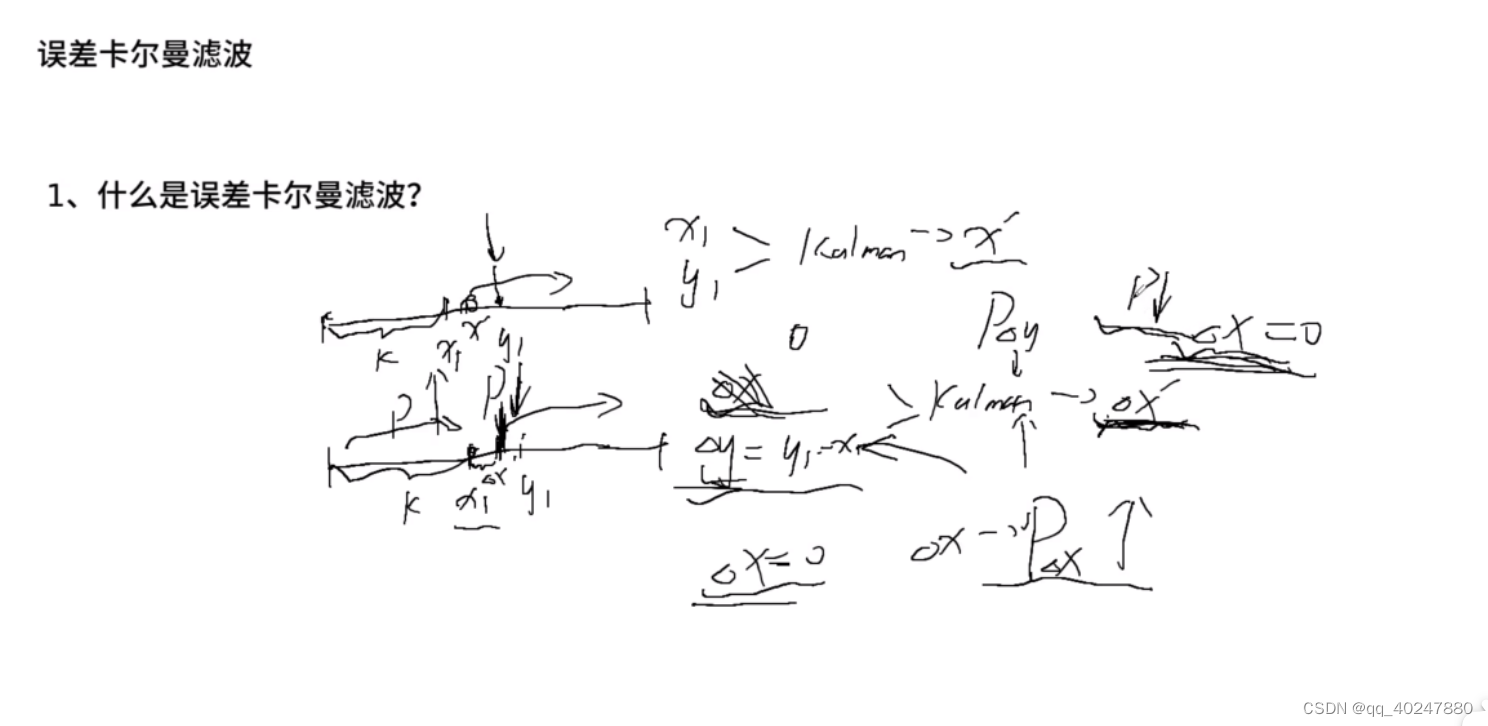
误差卡尔曼优势：1不用过参数化表示，用3维旋转向量，不用考虑协方差矩阵各维之间的约束。2靠近原点，没有万向节问题。3，忽略二阶导数，雅可比容易计算。4更新可以比较慢，因为误差比较小

true真值。nominal：名义值，包含噪声。

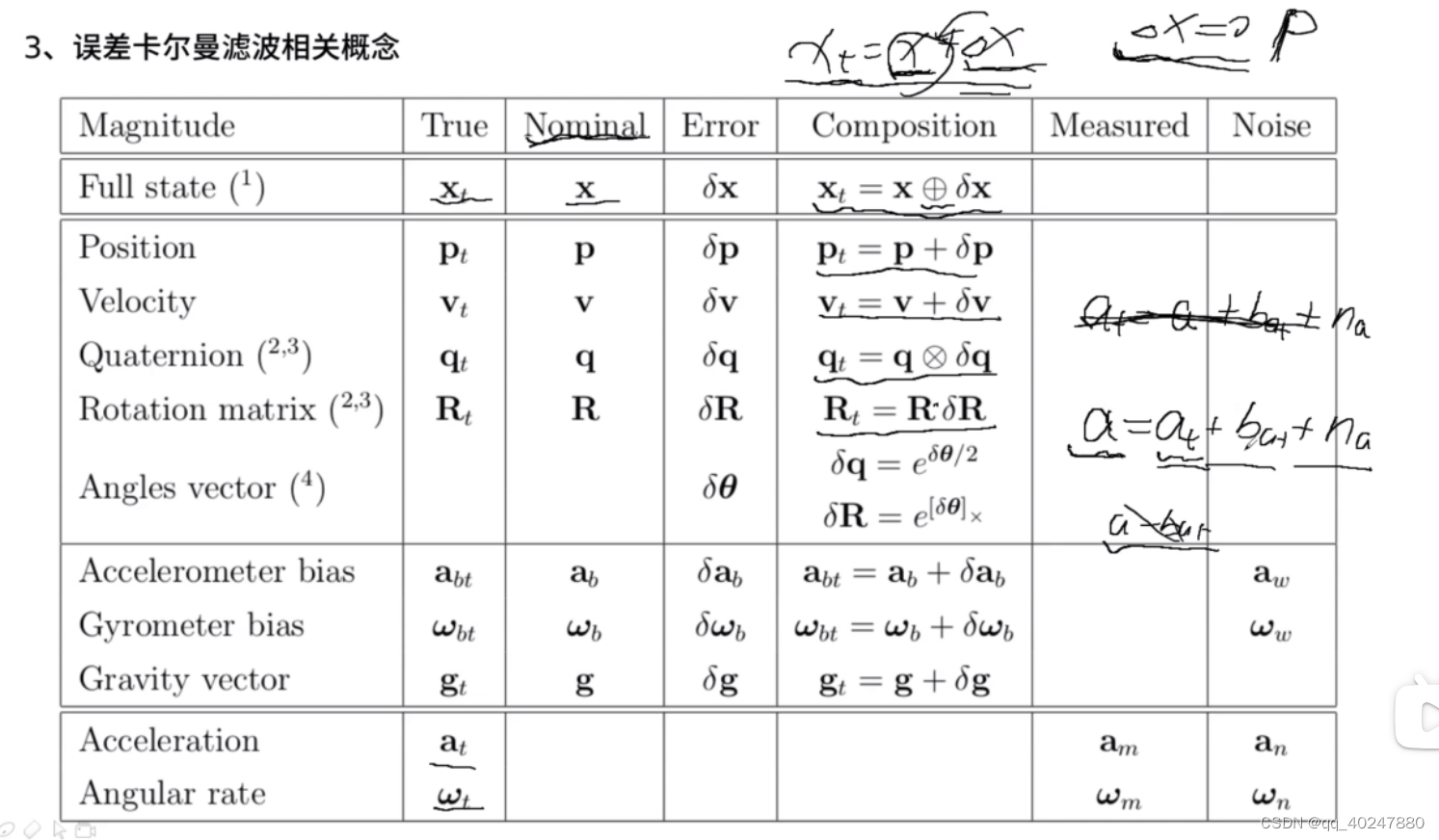
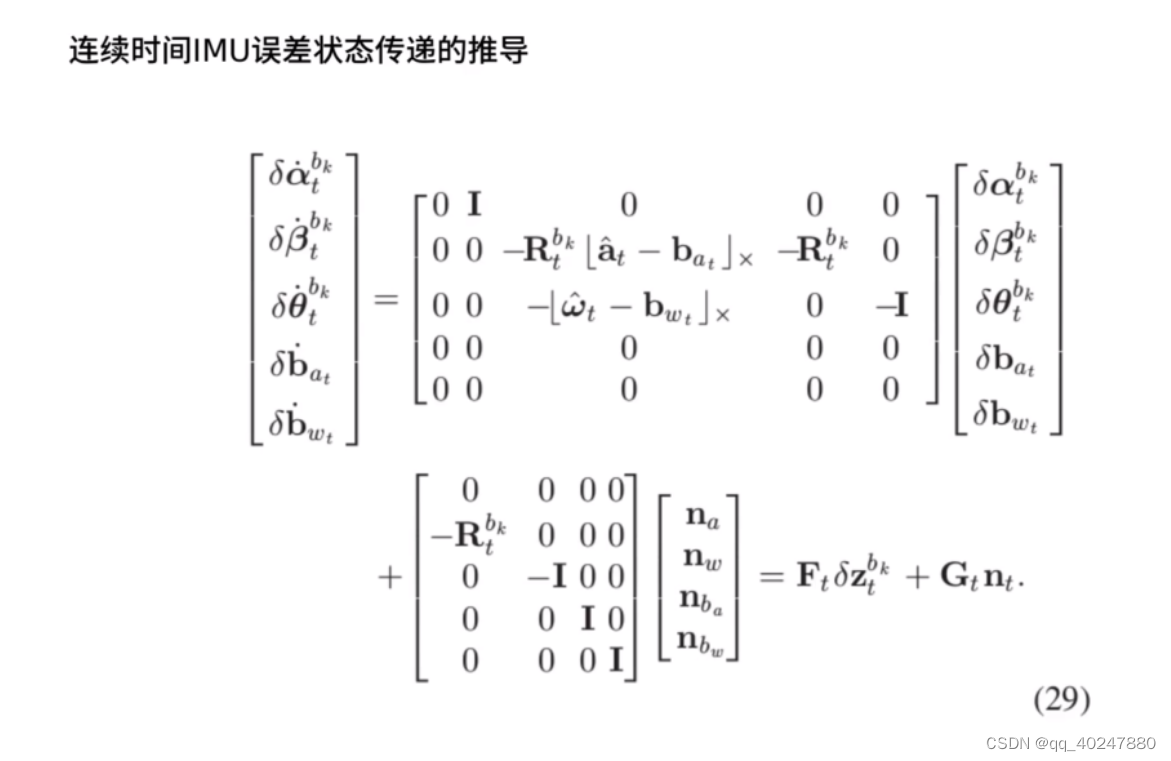
上面公式目的，在已知连续误差的变化量deltax，求deltaxk到deltaxk+1的矩阵变化。F就是Xk+1=Xk+J * delXk中的J。Jk+1=F Jk。。公式里协方差矩阵代码，代码与上面公式一样，除了噪声差一个负号，白噪声加减没区别。

零偏也是在更新的，需要用一阶近似求更新。F作用1，更新雅可比，方便状态量对零偏的更新，作用2，更新协方差矩阵，置信度

第四章vio初始化