递归算法学习

在这里插入图片描述

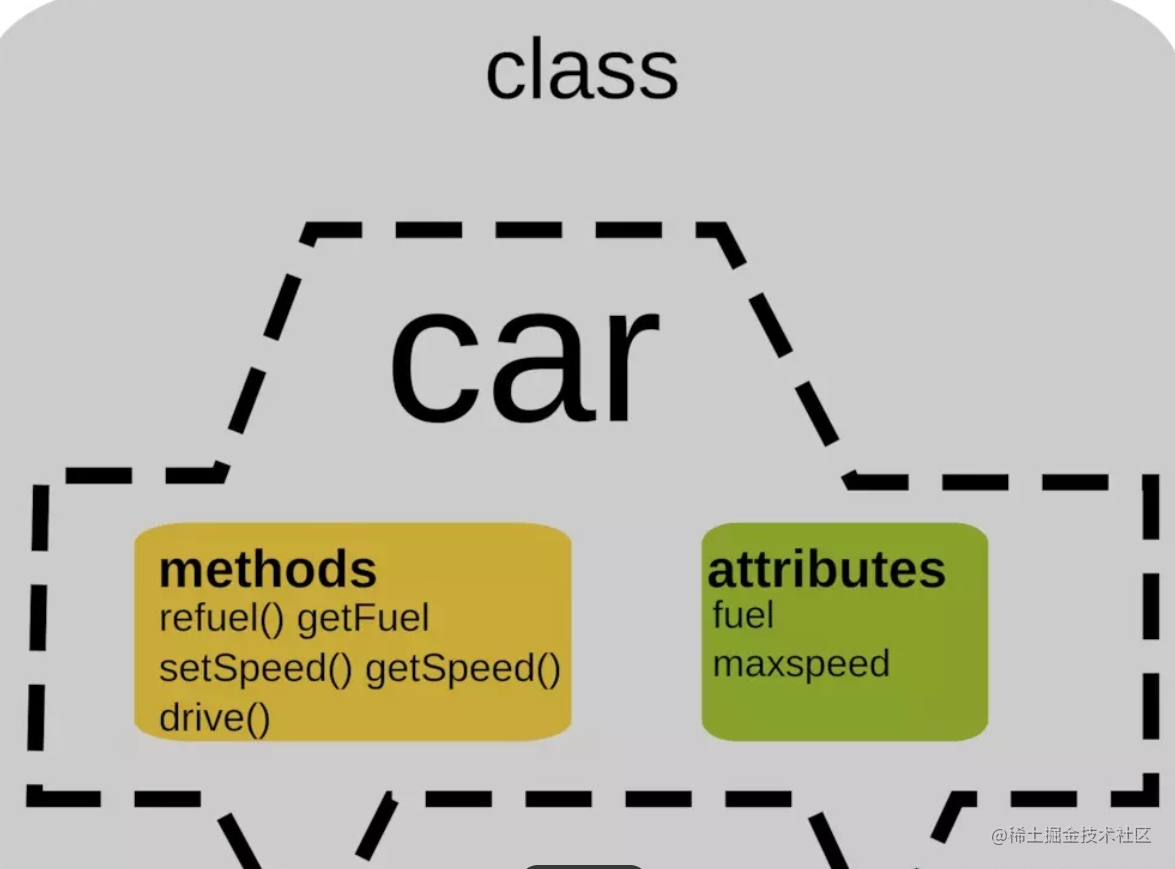
递归算法介绍

递归指的是函数或算法在执行过程中调用自身。在递归的过程中，程序会不断地将自身的执行过程压入调用栈中，直到满足某个条件结束递归调用并开始返回。递归算法常用于解决一些具有递归结构的问题，比如树、图、排序等。递归算法可以使代码更加简洁明了，但也需要注意递归深度、算法效率和内存占用等问题。

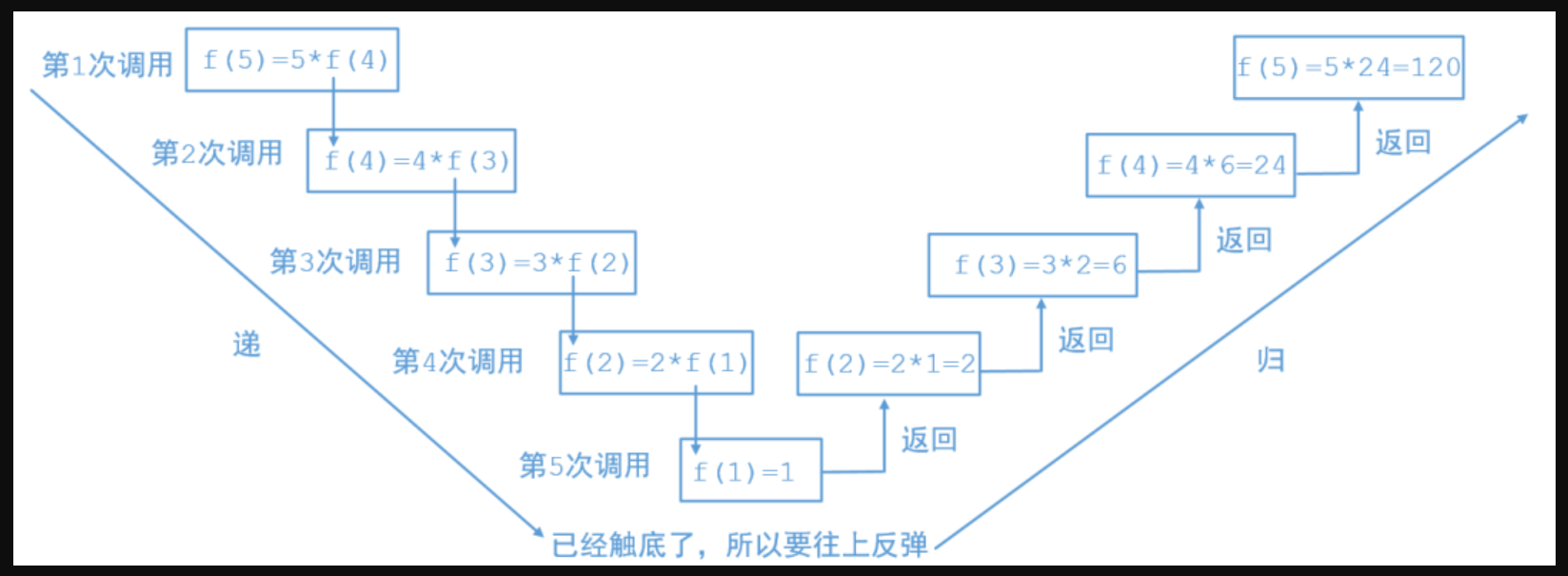
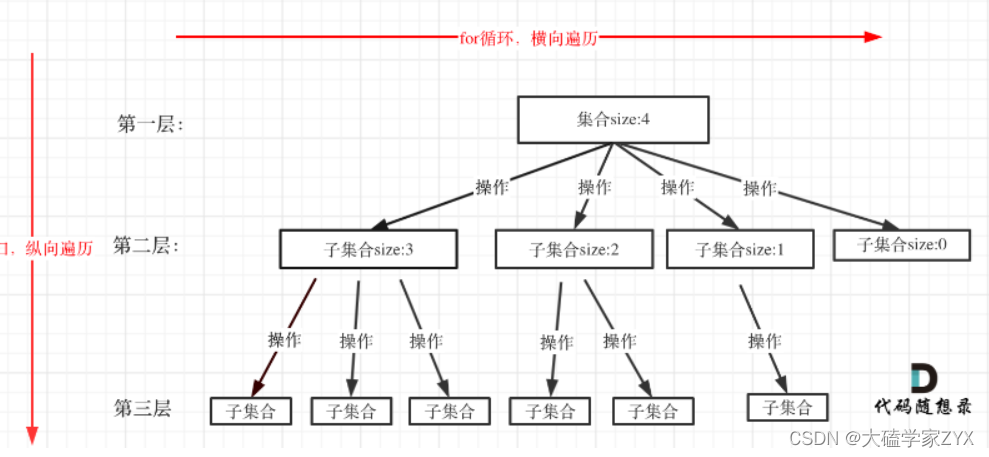
通俗的说，递归就像是一个函数在执行时，需要重复调用自己来完成它的任务。这有点像一个人从一层楼爬到另一层楼，如果每层楼的高度一样，那么他就可以一直重复爬楼梯，直到到达目标楼层为止。但是，如果楼层高度不一样，那么他需要考虑更多的事情，这时他就需要仔细思考每一步，并把每一步都记录下来，以便后面使用。递归算法也是这样，每一次重复调用相当于在上一次调用的基础上再做一些事情，直到到达“楼顶”（即达成某个条件），然后再逐层返回。上面的图片来自于网络，非常友好的解释了这一算法，非常形象！

递归算法适用场景

递归算法通常适用于以下几种场景：

树形结构：树形结构是递归的典型应用场景之一。树是由节点和边组成的，每个节点可以有多个子节点，子节点又可以作为父节点继续分叉。例如二叉树、多叉树、字典树等，都是递归算法的经典应用场景。

排序算法：一些排序算法，例如快速排序、归并排序等，都可以使用递归算法来实现。这些排序算法都采用了分治法的思想，即将一个大问题分解为多个小问题并分别解决，然后将这些小问题的解合并起来得到整个问题的解。

动态规划算法：动态规划算法是一种常用的优化算法，它可以将大问题分解为小问题并分别解决，然后将这些小问题的解合并起来得到整个问题的解。在动态规划算法中，递归也是一种常用的解决方式。

总之，递归算法适用于那些具有递归结构的问题，可以将复杂问题分解为简单问题并分别解决，然后将这些简单问题的解合并起来得到复杂问题的解。

递归算法使用注意项

在使用递归算法的时候，需要特别注意以下几个方面：

递归深度：递归调用过多会导致调用栈溢出，因此需要控制递归深度，避免递归层数过深而导致程序崩溃。

算法效率：递归算法的时间复杂度有时候可能比较高，因此需要对算法进行优化，避免产生过多的计算，提高算法效率。

内存占用：递归算法会造成一定的内存开销，因为每一次递归调用都需要将方法的调用数据保存在栈中。如果递归调用次数过多，会导致内存占用过大，可能会导致内存溢出或程序崩溃。

边界条件：递归算法必须设置边界条件，以保证递归过程的正确性。边界条件是指确定递归何时终止的条件，通常是在递归到最小或最大问题实例时。

总之，使用递归算法需要谨慎，需要考虑递归深度、算法效率、内存占用和边界条件等问题，以保证算法的正确性和性能。

计算斐波那契数列（Fibonacci Sequence）

一个经典的递归算法例子是计算斐波那契数列（Fibonacci Sequence）。斐波那契数列是一个数列，其中每个数字是前两个数字之和。

以下是使用Python实现斐波那契数列的递归算法：

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return (fibonacci(n-1) + fibonacci(n-2))

# 测试
n = 6
result = fibonacci(n)
print("斐波那契数列第", n, "项为:", result)

在这个例子中，fibonacci() 函数通过递归方式计算斐波那契数列的第 n 项。当 n<=1 时，直接返回 n。
对于其他大于1的值，通过调用自身来计算前两个数列项的和，并返回结果。

以上代码输出示例：

斐波那契数列第 6 项为: 8

该递归算法简洁地实现了斐波那契数列的计算，但需要注意的是，随着 n 的增加，递归的层数也会相应增加，可能导致性能上的问题。在实际应用中，可以考虑使用迭代或其他优化方式来改进算法性能。

递归实现的求阶乘

下面是一个用递归实现的求阶乘的python函数：

def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n-1)
result=factorial(5)
print("5的阶乘为：",result)

5的阶乘为： 120

在上面的代码中，我们定义了一个名为factorial的函数，它接受一个整数n作为输入。当n等于1时，返回1；否则，返回n与函数factorial(n-1)的乘积。这里，函数factorial反复调用自身来计算出n的阶乘。例如，当输入n=5时，函数factorial依次调用了factorial(4)、factorial(3)、factorial(2)、factorial(1)，最后得到5 x 4 x 3 x 2 x 1 = 120，即5的阶乘。

递归算法遍历二叉树

二叉树是一种特殊的树型结构，它每个节点最多只有两个子节点，分别称为左子节点和右子节点。对于二叉树上的每个节点，它的左子树和右子树也都是一个二叉树。二叉树的节点可以是任意类型的数据，包括整数、浮点数、字符串、自定义对象等。

下面是一个二叉树的图例：
     5
    / \
   3   8
  / \   \
 1   4   9
在上面的二叉树中，根节点的值为5，左子树的节点1、3、4组成一棵二叉树，右子树的节点8、9组成另外一棵二叉树。

二叉树的一个重要应用是作为搜索树。搜索树是一种特殊的二叉树，它的每个节点的值都大于其左子节点的值，小于其右子节点的值。搜索树可以使用二叉查找算法进行快速的查询、插入和删除。另外，二叉树还可以用来表示表达式、构建哈夫曼树等。在计算机科学中，二叉树是一种非常重要的数据结构。

二叉树在计算机科学中有广泛的应用场景，以下是一些二叉树的使用场景：

搜索和排序：二叉搜索树是一种使用二叉树实现的查找和排序算法。二叉搜索树具有很高的查找和排序速度，因为每个节点都可以利用它的二叉树性质来缩小查找范围。

表达式树：二叉树可以用来表示算术表达式，这可以简化计算机的求值过程。例如，一棵表达式树的中序遍历结果就是树代表的表达式。

文件系统：许多操作系统使用二叉树来组织文件系统。目录树结构可以使用二叉树来实现，每个目录就是一个节点，每个目录都可以包含多个子目录或文件。

数据压缩：Huffman编码是一种基于二叉树的无损数据压缩算法。在编码和解码过程中，二叉树被用于表示字符编码和解码方式。

线段树：线段树是一种使用二叉树实现的数据结构，它可以有效地处理线段区间问题。例如，求解区间最小值、区间最大值、区间和等问题。

总之，二叉树在算法、数据结构、编译器、操作系统等领域都有广泛的应用，是计算机科学中非常基础和重要的数据结构之一。

下面是一个使用递归算法遍历二叉树的例子：

假设我们有一个二叉树的节点定义如下：

class TreeNode():
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

有了节点的定义之后，我们可以考虑使用递归算法实现二叉树的遍历。下面是三种遍历方式的具体实现：

前序遍历（Pre-order Traversal）：先遍历根节点，然后遍历左子树，最后遍历右子树。

def pre_order_traversal(node):
    if node is None:
        return
    print(node.val)
    pre_order_traversal(node.left)
    pre_order_traversal(node.right)

中序遍历（In-order Traversal）：先遍历左子树，然后遍历根节点，最后遍历右子树。

def in_order_traversal(node):
    if node is None:
        return
    in_order_traversal(node.left)
    print(node.val)
    in_order_traversal(node.right)

后序遍历（Post-order Traversal）：先遍历左子树，然后遍历右子树，最后遍历根节点。

def post_order_traversal(node):
    if node is None:
        return
    post_order_traversal(node.left)
    post_order_traversal(node.right)
    print(node.val)

在上述三个函数中，都是使用递归的方式遍历二叉树。每次遍历时，都先检查当前节点是否为空，如果不为空，则分别调用递归函数遍历左子树和右子树，并输出当前节点的值。这样我们就可以通过递归实现二叉树的遍历了。

递归算法设计迷宫案例

下面是一个用递归算法解决迷宫问题的例子，假设我们已经有了一个 $m$ 行 $n$ 列的迷宫，其中 $0$ 表示通路， $1$ 表示障碍物， $S$ 表示起点， $G$ 表示终点，它们的定义如下：

maze = [
    [0, 1, 0, 0, 0, 1],
    [0, 1, 0, 1, 0, 1],
    [0, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 1, 0],
    [0, 0, 0, 0, 0, 0],
]

START_POS = (0, 0)  # 起点坐标
GOAL_POS = (4, 5)   # 终点坐标

要求我们编写递归函数 maze_solver(pos) ，用于求解从起点出发到达终点的一条通路，其中 pos 表示当前访问的位置的坐标 (row, col)。

def maze_solver(pos):
    # 边界条件
    if pos == GOAL_POS:  # 已经到达终点
        return True
    if not is_valid(pos):  # 当前位置无效
        return False
    if is_visited(pos):  # 当前位置已经被访问过了
        return False
    
    # 处理当前位置
    add_visited(pos)  # 标记当前位置已被访问
    
    # 递归访问上下左右四个方向
    if maze_solver((pos[0]-1, pos[1])):  # 上
        add_path(pos)
        return True
    elif maze_solver((pos[0]+1, pos[1])):  # 下
        add_path(pos)
        return True
    elif maze_solver((pos[0], pos[1]-1)):  # 左
        add_path(pos)
        return True
    elif maze_solver((pos[0], pos[1]+1)):  # 右
        add_path(pos)
        return True
   
    return False  # 无路可走的情况


# 工具函数：检查当前位置是否是通路
def is_valid(pos):
    i, j = pos
    if 0 <= i < len(maze) and 0 <= j < len(maze[0]) and maze[i][j] == 0:
        return True
    return False

# 工具函数：查找当前位置是否已经被访问过
visited = set() 

def is_visited(pos):
    return pos in visited

# 工具函数：将当前位置标记为已访问
def add_visited(pos):
    visited.add(pos)

# 工具函数：将路径添加到路线中
path = []

def add_path(pos):
    path.append(pos)

# 执行迷宫求解
maze_solver(START_POS)

# 输出结果
print(path)  # [(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (3, 2), (3, 3), (3, 4), (4, 4), (4, 5)]

在上述代码中，我们使用了递归算法实现了从起点开始搜索迷宫通路的过程。在每个位置上，我们先检查当前位置是否有效，即当前位置是否越界或者是否是障碍物；如果当前位置有效，我们则将当前位置标记为已访问。接着我们递归访问当前位置的四周位置，如果有一条通路可以到达终点，我们则将当前位置加入路线中，并返回True。如果四周都无法到达终点，则返回False。