一、D-star Lite算法简介
1994年 Anthony Stentz在论文Optimal and Efficient Path Planning for Partially-known Environments中提出了D*算法
D * 算法采用逆向搜索,从目标点向起始点搜索规划,可以处理环境部分未知或全部未知以及动态障碍的一些情况。此算法被作为路径规划的核心算法应用于美国1996年发射的火星探测器上,并获得了很大的成功。
基于反向搜索思想的D*算法能够很好的处理动态障碍这种情况,虽然可以实现未知环境的路径规划,但效率较低。
1995年,Anthony Stentz又于在论文The Focussed D * Algorithm for Real-Time Replanning中提出了Focused D * 算法,重点提高了D*算法的实时性
2001年,Sven Koenig和Maxim Likhachev首次提出了LPA * 算法。
LPA * ( Lifelong Planning 终身规划 A * )是一种基于A * 的增量启发式搜索算法,被用来处理动态环境下从给定起始点到给定目标点的最短路径问题,即起始点和目标点是固定的。
LPA * 算法能够在环境的障碍发生突变时,最大限度的利用前一次的搜索结果,从而快速进行第二次规划,但LPA * 算法只能求解定起点和定终点之间的最优路径问题,在遭遇动态障碍物进行第二次路径规划时受影响的节点较多,计算量较大。
2002年,Sven Koenig和Maxim Likhachev在论文D* Lite中首次提出D * Lite算法
2005年,Sven Koenig和Senior Member在论文Fast Replanning for Navigation in Unknown Terrain中对提出D * Lite算法进行了进一步描述。
D * Lite是也是一种增量的、启发式的规划算法,它完成的功能和Focussed Dstar相似,但从算法设计的角度来看,它们有着不同的思路。D * Lite算法融合了LPA * 算法的增量搜索思想、D * 算法的反向搜索思想,是一种变起点的反向增量式动态路径搜索算法。

二、D * 算法与LPA * 算法基础
为了更好的了解D * lite算法,我们先简单了解一下D * 算法(选做),重点了解掌握一下LPA * 算法,本部分内容在前面的文章中已经做了介绍,本文中不再介绍,链接如下:
xxx:【点击此处跳转】
LPA-star算法(Lifelong Planning)及相关思考:【点击此处跳转】
三、在LPA * 算法的基础上看D * Lite算法
1、D * Lite算法LPA * 算法的重大差异
① k1值的不同:D * Lite算法的k1的计算组成中,在LPA * 的min(g(s),rhs(s))+ h(s,sstart)的基础上增加了km项,km值表示机器人当前位置与算法运行后第一次静态规划的起始位置的距离(代价值),如下图所示。
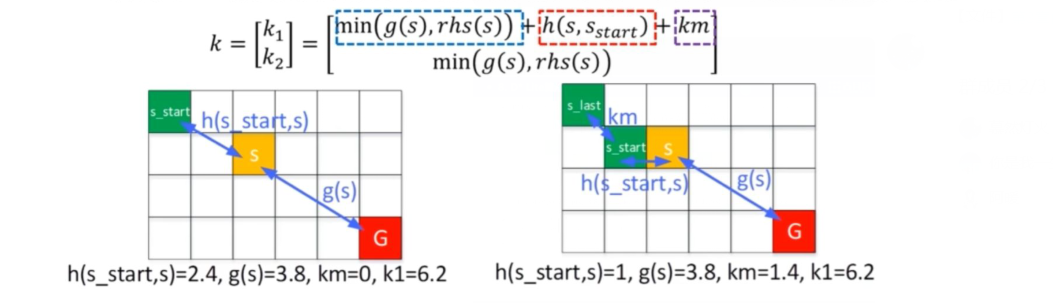
km值的作用是什么呢? 当算法运行并成功规划出第一次的静态路径后,机器人开始沿着该路径向目标位置移动,若移动过程中出现的动态障碍物导致第一次规划的路径不可行后,开始进行动态规划,并将机器人当前的位置作为新的起点,对于此后的点计算的h值是拓展点与机器人当前位置的距离(代价值),而对于之前第一次规划时计算的h值,则是拓展点与机器人第一次静态规划时的起点的距离(代价值),此时,我们想要在本次规划时使用之前规划搜索时得到的先验信息,便产生了冲突。
一种解决该冲突的方法是,将U队列中的所有点的h值减去km,来将h值统一成拓展点到机器人当前位置的距离(代价值),但是当U队列中节点较多时,这样做会耗费较多的计算资源,效率较低。若机器人再次移动后,依然需要将U中所有点的h值再次更新一下。
另外一种解决该冲突的方法,也就是D * Lite采用的方法是,将新加入到U队列中的点的h值都加上km,来将(h+km)值的整体统一成拓展点到算法运行后第一次静态规划的起始位置的距离(代价值),此种方法可以在耗费较低的计算资源的基础上,解决以上冲突,效率较高。
② 搜索方向的不同:与LPA * 的正向搜索不同的是,D * Lite算法采用跟D * 算法类似的反向搜索策略,即从目标点向起始点搜索。
③搜索方式不同:LPA * 采用的是定起点和终点的搜索方式,当机器人开始移动后,即起始点改变后,在移动过程中出现的新的障碍物使得当前路径不可行后,便需要重新进行静态规划,不能很好的利用之前规划的信息(这一点从LPA * 没有考虑①中介绍冲突也能体现出来 ),而D * Lite算法则是动起点的搜索方式,即使机器人的当前位置已经发生了改变,依然可以很好的使用之前规划的信息进行动态规划,而不需要重新进行无先验信息的静态规划。
2、在LPA * 算法的基础上看D * Lite算法流程
首先,将当前的起点赋值给Slast,更新上一次的起点,便于后续计算△km,然后执行初始化部分Initialize(),除将目标点的rhs值设为0,将终点加入到U队列中之外,其余部分与LPA*基本相同。然后执行ComputeShortestPath()函数,与LPA * 不同的是,D * Lite新增了判断当前拓展点是否被影响的程序,若k_old小于节点u计算的k值,表明节点u的k值受到周围节点的影响而做过修改,故应当重新插入到U队列中,不再进行本次拓展,重新从U队列中取k值最小的节点进行拓展。ComputeShortestPath()函数的其余部分与LPA * 相同,不再进行介绍
执行完ComputeShortestPath函数后,第一次静态规划就结束了,机器人开始沿着该路径向目标点移动,伪代码里面介绍的方法是从当前点开始向周围八邻域节点中代价值(g值)较小的那个节点移动,其实环境未发生变化时,与沿着静态规划的路径移动是等效的。
在移动过程中,若发现新出现的动态障碍物导致之前规划的路径不可行后,先更新km值,km=km+△km=km+h(Slast,Sstart),并当前起点Sstart赋值给Slast,更新上一次的起点信息。剩下的操作就与LPA* 类似了,找到所有受影响的节点,然后将突变为障碍物的节点的rhs和g值均设为inf,将受影响的节点的rhs值设为inf,并加入到U队列中,然后调用ComputeShortestPath函数动态规划新的路径。

-

四、D * Lite算法流程示例

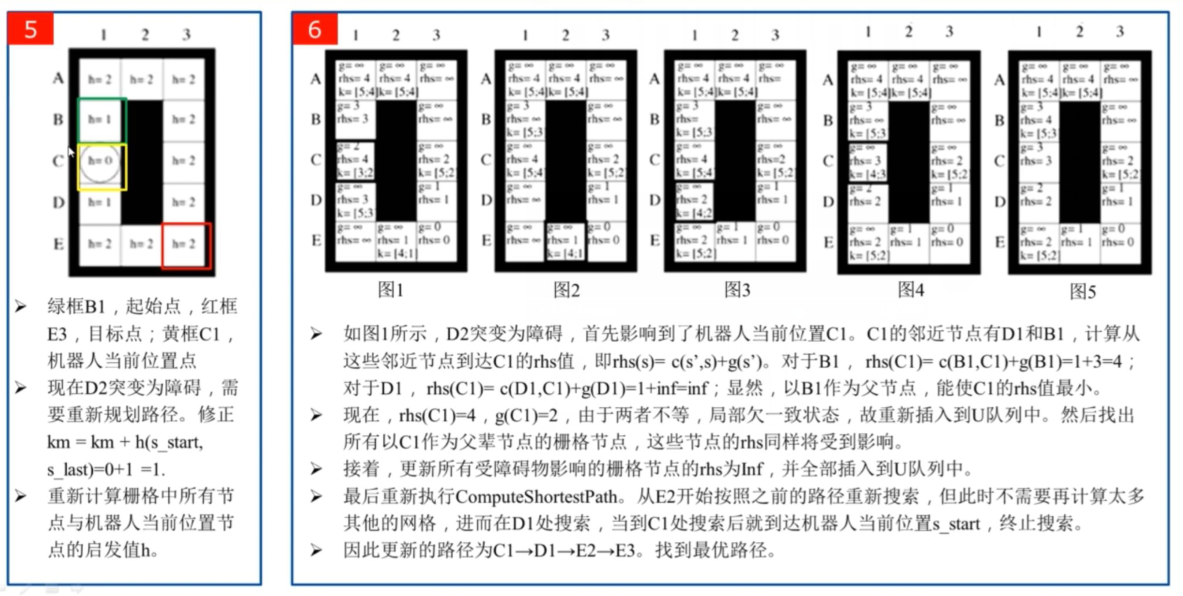
五、D * Lite优化版本
除了上面介绍的D * Lite版本,原作者还在论文中给出了其多优化版本的伪代码,如下所示。

主要参考资料:
1、古月学院 基于栅格地图的机器人路径规划算法指南:【点击此处跳转】
2、D * 算法:【点击此处跳转】

![[附源码]计算机毕业设计勤工助学管理系统Springboot程序](https://img-blog.csdnimg.cn/7456fd0e8e6e41d1b3c0b49f650067ac.png)


![[附源码]JAVA毕业设计人才公寓管理系统(系统+LW)](https://img-blog.csdnimg.cn/88bb425fb385432a9383d5ca9ccdb197.png)