文章目录
- 一、前言
- 二、相关资源
- 三、下载安装初始化
- 1、下载PSINSyymmdd.rar工具箱文件
- 2、解压文件
- 3、初始化
- 4、启动工具箱导览
- 四、习惯约定与常用变量符号
- 1、PSINS全局变量结构体 glv
- 2、坐标系定义
- 3、姿态阵/姿态四元数/欧拉角 Cnb/qnb/att
- 4、IMU采样数据 imu
- 5、AVP导航参数 avp
- 6、误差参数
- 7、其它常用变量
- 1.角速率 wnie
- 2. 不可交换误差补偿 phim/dvbm
- 3.重力矢量 gn
- 4.有害加速度 gcc
- 5.仿真轨迹结构体 trj
- 6.指北方位捷联导航解算结构体 ins
- 7.导航地球相关计算结构体 eth
- 8.Kalman滤波结构体 kf
- 五、数据导入、转换
- 六、绘图显示
- 1、绘图辅助函数
- 2、传感器数据绘图
- 3、导航结果绘图
- 4、进度条函数
- 七、SINS/GPS组合导航仿真举例
- 1、生成仿真轨迹
- 2、纯惯导仿真
- 3、SINS-GPS仿真
一、前言
PSINS(Precise Strapdown Inertial Navigation System 高精度捷联惯导系统算法)工具箱由西北工业大学自动化学院惯性技术教研室严恭敏老师开发和维护。工具箱分为Matlab和C++两部分。主要应用于捷联惯导系统的数据处理和算法验证开发,它包括惯性传感器数据分析、惯组标定、初始对准、惯导AVP(姿态-速度-位置)更新解算、组合导航Kalman滤波等功能。C++部分采用VC6编写,可以用于嵌入式开发。
如果你之前还没接触过PSINS工具箱,强烈建议先去看严老师的 视频讲解,再看严老师的 硕士论文。把 PSINS网站 上的资料全部下载下来作为学习PSINS工具箱的参考。
本人导航工程大二学生,之前还写了 RTKLIB 、GraphGNSSLib 、测绘程序设计 等系列的博客。初学惯导,认识尚浅,有错误欢迎指出。以往的也有一些PSINS的博客,我想在他们的基础上,写套比较系统的专栏。下面推荐一些已有的博客:
- 十八与她 的专栏 PSINS工具箱基本原理与应用
- 枯荣有常 的专栏 psins代码解析
- 路痴导航员 的 关于PSINS运动轨迹仿真模块的理解和思考 等
- waihekor 的 PSINS源码阅读—test_SINS_trj、PSINS源码test_SINS_DR解析 、PSINS C++代码移植与效果测试 等
- S1301060113 的 严恭敏老师PSINS工具箱解读——test_SINS_GPS_153、glvf 、imuadderr 等
二、相关资源
-
PSINS网站 可下载最新PSINS工具箱源码及课程PPT,导航数据。还有新浪博客、知乎 上有技术交流文章、推荐看知乎,一直在更新,排版也好一些。
-
PSINS导航算法QQ群:46819593,人快满了,不知道还能不能进了。
-
bilibili课程视频:卡尔曼滤波与组合导航原理【西北工业大学 严恭敏】:共10讲,先讲Kalman滤波,后讲捷联惯导算法。
- 01讲:递推最小二乘法、卡尔曼滤波方程的推导
- 02讲:连续时间系统的离散化、连续时间卡尔曼滤波、噪声相关条件下的卡尔曼滤波、序贯滤波
- 03讲:信息滤波与信息融合、平方根滤波
- 04讲:遗忘滤波、自适应滤波、量测故障检测与强跟踪滤波、滤波平滑、扩展卡尔曼滤波/二阶滤波/迭代滤波
- 05讲:无迹卡尔曼滤波、联邦滤波
- 06讲:滤波器稳定性分析、状态估计的误差分配与可观测度分析、最小方差估计与线性最小方差估计
- 07讲:极大似然估计、极大验后估计、加权最小二乘估计、维纳滤波、递推贝叶斯估计。向量及其反对称阵、方向余弦阵与等效旋转矢量
- 08讲:姿态阵微分方程及其求解、四元数微分分方程及其求解、等效旋转矢量微分方程及其泰勒级数解
- 09讲:圆锥运动条件下的多子样优化算法、地球形状及重力场
- 10讲:捷联惯导全套数值更新算法、误差传播方程、初始对准、SINS/GNSS组合导航
- 有些没听明白的可以看看配套的书《捷联惯导算法与组合导航原理》,书上讲的比PPT详细。
- 我刚学完,写了套《卡尔曼滤波与组合导航原理》博客,对讲的内容梳理了一下,写的不好,看我这个博客不如直接看书。
- B站的视频是2020年的,现在2023年严老师还在讲课,腾讯会议上每周日开讲(会议号:875 3929 3450),有录屏可以看。直播的开始老师会讲解学生之前的程序作业,此部分没有录屏。
-
bilibili课程视频:PSINS导航工具箱入门与详解【西北工业大学 严恭敏】 :共4讲,对工具箱的功能、使用方式、原理做了很详细的讲解。
- 第一课:工具箱简介、下载与安装初始化、快速开始—SINS/GNSS组合导航仿真举例
- 第二课:习惯约定与常用变量符号、导入数据文件与数据提取转换、绘图显示、姿态阵/姿态四元数/欧拉角/等效旋转矢量之间的转换函数
- 第三课:运动轨迹与惯性器件信息生成仿真、惯性器件误差模拟与分析、不可交换(圆锥/划桨)误差补偿、捷联惯导更新算法、初始对准方法、卡尔曼滤波与SINS/GNSS组合导航、捷联惯导的系统级标定
- 第四课:C++导航库函数
-
PSINS开发板:bilibili介绍视频、淘宝链接、780元

三、下载安装初始化
1、下载PSINSyymmdd.rar工具箱文件
直接在PSINS网站 www.psins.org.cn 下载,yymmdd—“年年月月日日”表示版本信息,选一个最新版的下就行。我用的版本是psins230321。
2、解压文件
建议在D盘根目录,文件解压完之后不要改动任何文件夹名称,各子文件夹功能:
- base:核心算法、数据预处理及图形显示等库函数。
- data:用于工具箱提供的样本数据、生成中间数据、或用户输入输出存放数据;为了控制文件大小,很多数据没放在里面,PSINS网站上还有很多。
- demos:一系列演示和测试例子。
- dlg:可视化(对话框)应用例子。
- doc:工具箱介绍和使用说明等文档;除此以外每个matlab文档上面有一个
help也对用法做了介绍。 - gnss:仅试图用于SINS/GNSS紧组合中卫导信号处理,不太专业。
- mytest:建议用户修改、编写的测试和应用例子放在该文件夹下;如果更新的版本,把mytest复制出来就行,减小冲突。
- vc60:VC6.0工程文件夹,导航核心算法用C++编写,可移植于嵌入式应用:核心算法、数据预处理及图形显示等库函数;
3、初始化
启动Matlab软件,打开PSINS根目录下的psinsinit.m文件,运行,即可完成工具箱的安装初始化。
- 初始化过程也就是将PSINSyymmdd及其所有子文件夹添加到Matlab的搜索路径下并保存路径设置;
- 初始化之后尽量不要改动PSINS文件夹位置,改动要重新初始化。
- 新版本的安装初始化会移除以往添加到Matlab的含“PSINS”字符的所有路径,减小冲突。
- 不要自己用
addpath添加路径,如果下多个版本,可能会冲突。
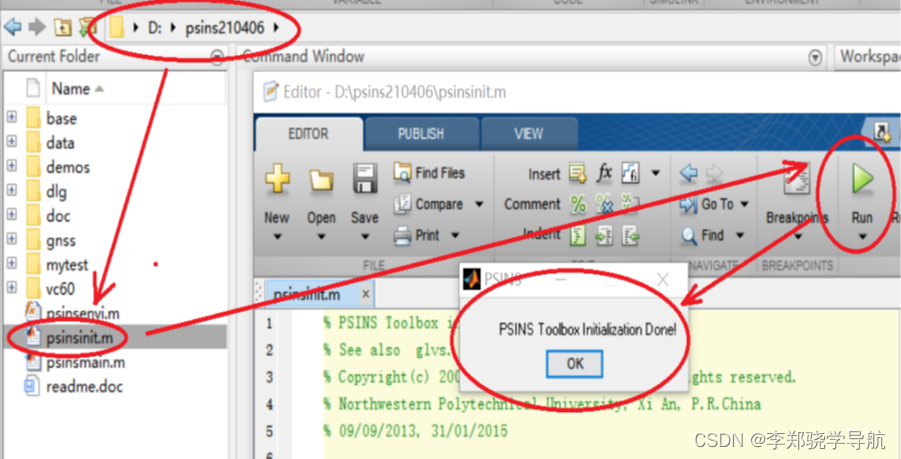
4、启动工具箱导览
打开PSINS根目录下的psinsmain.m文件,运行,启动“工具箱导览”主界面,点击相应按钮可感受工具箱的主要演示/测试例子;如果勾选了左上角的“查看m文件源码”,再点按钮就是阅览相应的程序源代码。

四、习惯约定与常用变量符号
- PSINS里的变量很多都是简写,这里给出一些常用的,看完这些再看代码会比较容易一些。
- 工具箱中所有的物理量在内部计算都使用标准单位,比如角度用 r a d rad rad、比力用 m / s 2 m/s^2 m/s2 等。只有在初始化输入参数时才会用习惯单位。
- 有角标的符号书写一般遵从规律是从左到右从上到下。
1、PSINS全局变量结构体 glv
它是 global variable 的缩写,内容可以在 glvf 函数里看,运行脚本 glvs.m 即可初始化全局变量glv,一般在主文件都会先执行 glvs 初始化全局变量。
clear global glv
global glv
glv = glvf;
glvf函数有三个参数,Re是地球半径, f是地球扁率, wie是地球自转角速率,如果不传参数,默认WGS-84坐标系。
参考:严恭敏老师PSINS工具箱解读——glvf
function glv1 = glvf(Re, f, wie)
global glv
% 三个参数,Re是地球半径, f是地球扁率, wie是地球自转角速率,
% 如果不传参数,默认使用WGS-84坐标系
if ~exist('Re', 'var'), Re = []; end
if ~exist('f', 'var'), f = []; end
if ~exist('wie', 'var'), wie = []; end
if isempty(Re), Re = 6378137; end
if isempty(f), f = 1/298.257; end
if isempty(wie), wie = 7.2921151467e-5; end
glv.Re = Re; % the Earth's semi-major axis 长半轴
glv.f = f; % flattening 扁率
glv.Rp = (1-glv.f)*glv.Re; % semi-minor axis 短半轴
glv.e = sqrt(2*glv.f-glv.f^2); glv.e2 = glv.e^2; % 1st eccentricity 第一偏心率
glv.ep = sqrt(glv.Re^2-glv.Rp^2)/glv.Rp; glv.ep2 = glv.ep^2; % 2nd eccentricity 第二偏心率
glv.wie = wie; % the Earth's angular rate 自转角速率
glv.meru = glv.wie/1000; % milli earth rate unit 自转角速率的千分之一
% 地球重力,g0:G、mg:毫G、ug:微G
glv.g0 = 9.7803267714; % gravitational force 重力
glv.mg = 1.0e-3*glv.g0; % milli g
glv.ug = 1.0e-6*glv.g0; % micro g
glv.mGal = 1.0e-3*0.01; % milli Gal = 1cm/s^2 ~= 1.0E-6*g0
glv.uGal = glv.mGal/1000; % micro Gal
glv.ugpg2 = glv.ug/glv.g0^2; % ug/g^2
glv.ws = 1/sqrt(glv.Re/glv.g0); % Schuler frequency 舒勒频率
glv.ppm = 1.0e-6; % parts per million 百万分之一
glv.deg = pi/180; % arcdeg 单位:弧度
glv.min = glv.deg/60; % arcmin 单位:弧分
glv.sec = glv.min/60; % arcsec 单位:弧秒
glv.mas = glv.sec/1000; % milli arcsec 单位:弧毫秒
glv.hur = 3600; % time hour (1hur=3600second) 一小时
% 陀螺仪
glv.dps = pi/180/1; % arcdeg / second 度每秒
glv.rps = 360*glv.dps; % revolutions per second 度每分钟
glv.dph = glv.deg/glv.hur; % arcdeg / hour 度每小时
glv.dpss = glv.deg/sqrt(1); % arcdeg / sqrt(second)
glv.dpsh = glv.deg/sqrt(glv.hur); % arcdeg / sqrt(hour)
glv.dphpsh = glv.dph/sqrt(glv.hur); % (arcdeg/hour) / sqrt(hour)
glv.dph2 = glv.dph/glv.hur; % (arcdeg/hour) / hour
glv.Hz = 1/1; % Hertz
glv.dphpsHz = glv.dph/glv.Hz; % (arcdeg/hour) / sqrt(Hz)
glv.dphpg = glv.dph/glv.g0; % (arcdeg/hour) / g
glv.dphpg2 = glv.dphpg/glv.g0; % (arcdeg/hour) / g^2
glv.ugpsHz = glv.ug/sqrt(glv.Hz); % ug / sqrt(Hz)
glv.ugpsh = glv.ug/sqrt(glv.hur); % ug / sqrt(hour)
glv.mpsh = 1/sqrt(glv.hur); % m / sqrt(hour)
glv.mpspsh = 1/1/sqrt(glv.hur); % (m/s) / sqrt(hour), 1*mpspsh~=1700*ugpsHz
glv.ppmpsh = glv.ppm/sqrt(glv.hur); % ppm / sqrt(hour)
glv.mil = 2*pi/6000; % mil
glv.nm = 1853; % nautical mile 单位:海里
glv.kn = glv.nm/glv.hur; % knot 单位:节-海洋中的速度单位
glv.kmph = 1000/glv.hur; % km/hour
%%
glv.wm_1 = [0,0,0]; % the init of previous gyro 陀螺仪角度增量
glv.vm_1 = [0,0,0]; % the init of previous acc sample 加速度计速度增量
glv.cs = [ % coning & sculling compensation coefficients 锥度和双桨补偿系数
[2, 0, 0, 0, 0 ]/3
[9, 27, 0, 0, 0 ]/20
[54, 92, 214, 0, 0 ]/105
[250, 525, 650, 1375, 0 ]/504
[2315, 4558, 7296, 7834, 15797]/4620 ];
glv.csmax = size(glv.cs,1)+1; % max subsample number 最大子样本数
glv.v0 = [0;0;0]; % 3x1 zero-vector 3x1 零向量
glv.qI = [1;0;0;0]; % identity quaternion 特征四元数
glv.I33 = eye(3); glv.o33 = zeros(3); % identity & zero 3x3 matrices
glv.pos0 = [34.246048*glv.deg; 108.909664*glv.deg; 380]; % position of INS Lab@NWPU
glv.eth = []; glv.eth = earth(glv.pos0); %利用earth函数计算地球的相关参数
glv.t0 = 0;
glv.tscale = 1; % =1 for second, =60 for minute, =3600 for hour, =24*3600 for day
glv.isfig = 1;
glv.dgn = [];
%%
[glv.rootpath, glv.datapath, glv.mytestflag] = psinsenvi;
glv1 = glv; % 返回全局变量的结构体
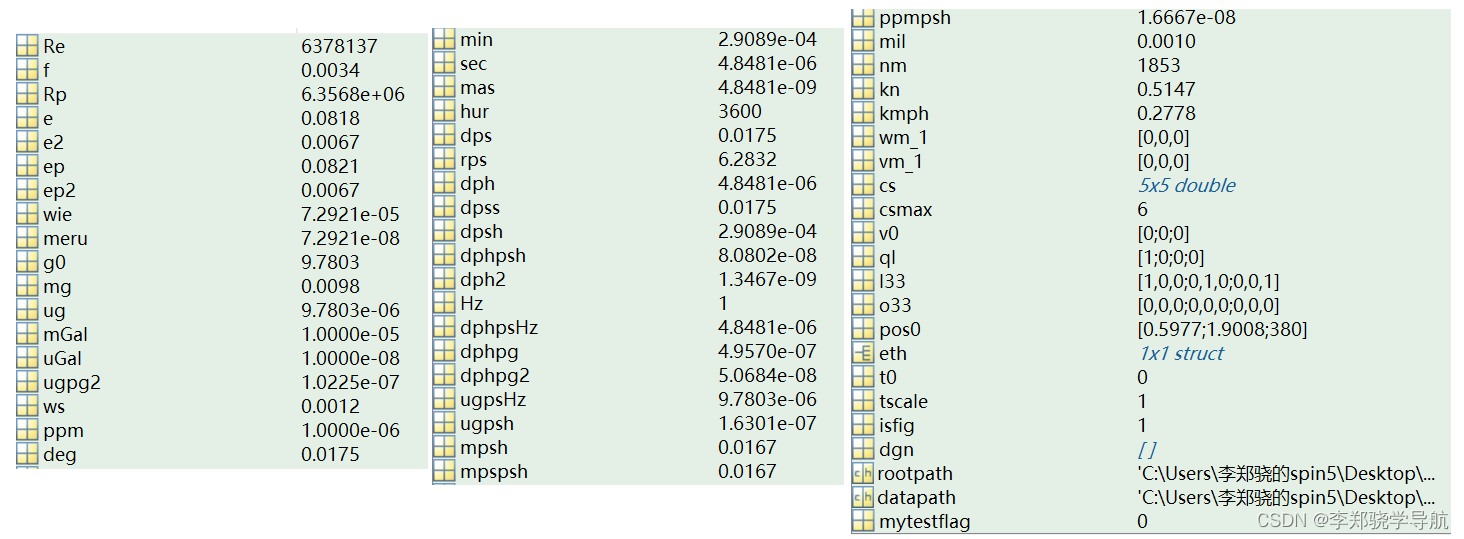
2、坐标系定义
- 惯性坐标系(i):陀螺仪和加速度计测量值的基准
- 地球坐标系(e):即ECEF坐标系
- 导航坐标系(n):东E-北N-天U
- 载体坐标系(b):右R-前F-上U
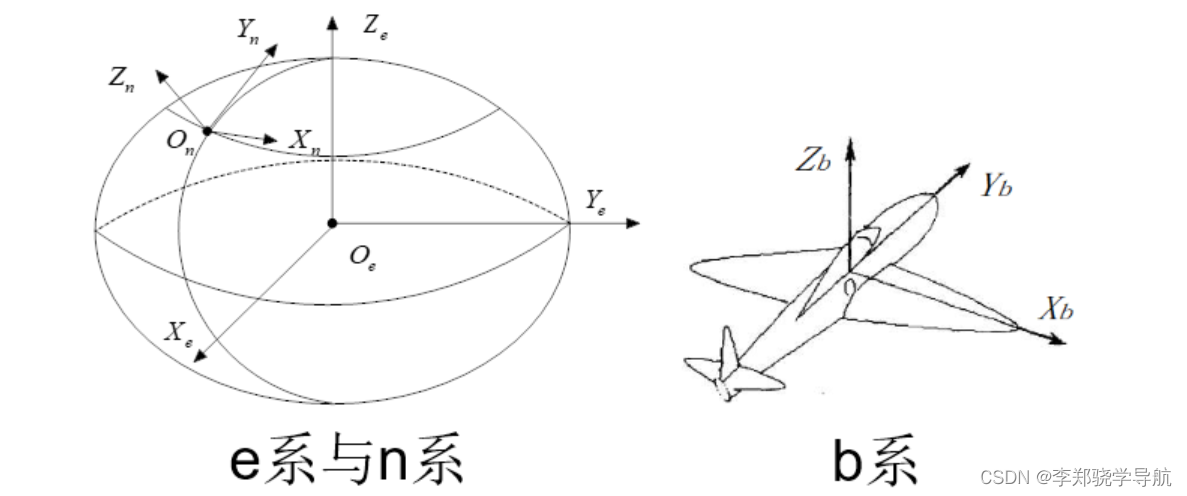
3、姿态阵/姿态四元数/欧拉角 Cnb/qnb/att
- 姿态阵:
Cnb,表示从 b 系到 n 系的坐标变换矩阵。对应姿态四元数写为qnb。 - 欧拉角:
att=[俯仰pitch; 横滚roll; 方位yaw]。没有按照转到顺序来写,如果按转到顺序,东北天坐标系转到右前下坐标系,常见先转方位角、然后俯仰角、横滚角
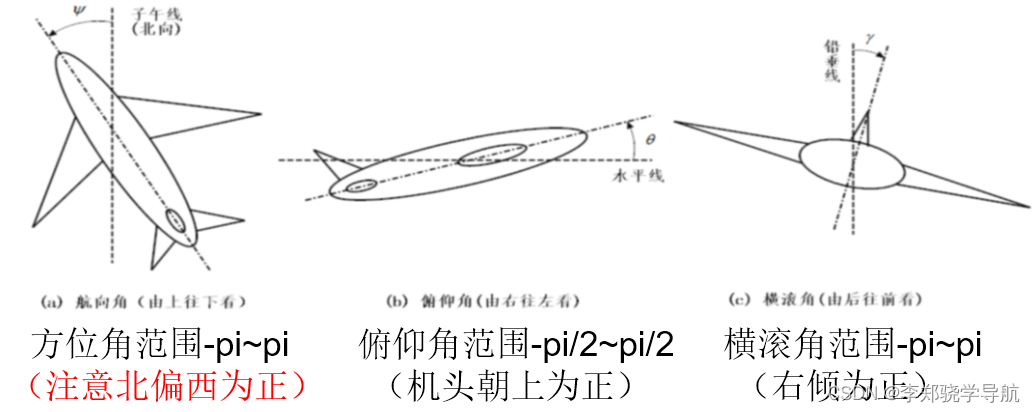
4、IMU采样数据 imu
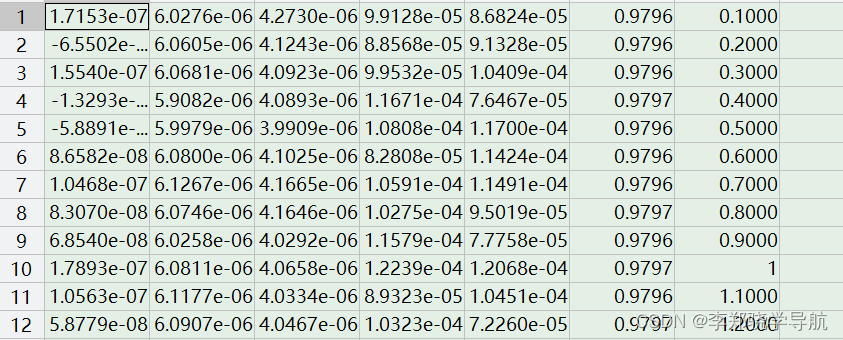
imu=[wm; vm; t] 其中:
wm为陀螺三轴角增量,是角速率积分,单位rad,1~3列,右前上。vm为加表三轴速度增量,是比力积分,单位m/s,4~6列,右前上。100Hz静止采样,第6列的数据是0.098左右,如果不是这种特征就有问题,IMU可以需要坐标转换。- PSINS惯导算法里使用的陀螺和加表输入都是增量信息,如果用户数据中是角速度/比力信息,则简单地乘以采样间隔
ts处理即可。 - 时标通常放在最后一列,imu一般都是等间隔采样,有些不等间隔的可能是因为时钟的抖动,可以平均转换成等间隔。
5、AVP导航参数 avp
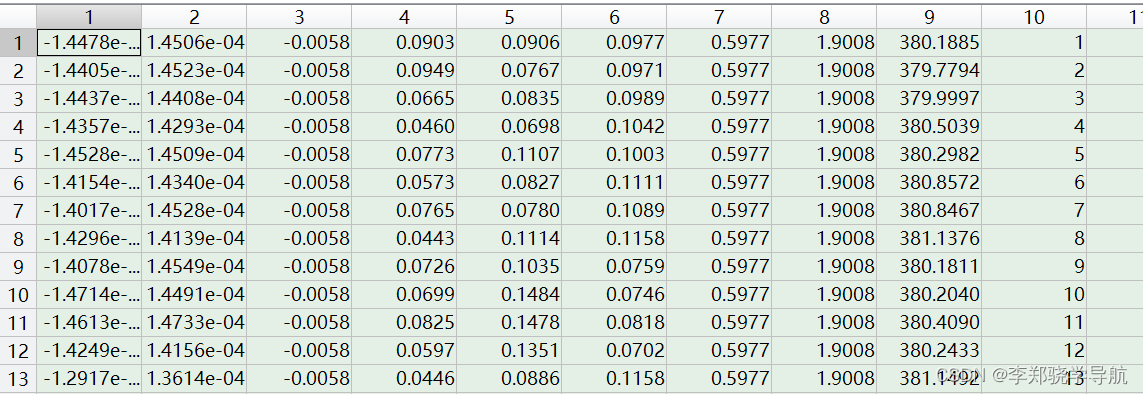
avp=[att; vn; pos; t]。其中:
- 姿态:
att=[俯仰pitch; 横滚roll; 方位yaw];单位rad - 速度:
vn=[东速vE; 北速vN; 天速vU]; - 位置:
pos=[纬度lat; 经度lon; 高度hgt];单位rad
6、误差参数
-
失准角误差
phi=[phiE;phiN;phiU];速度误差dvn;位置误差dpos=[dlat;dlon;dhgt];(d一般指误差 δ \delta δ) -
陀螺漂移
eb=[ebx;eby;ebz];加表零偏db=[dbx;dby;dbz];web为陀螺角度随机游走/角速率白噪声;wdb为加计速度随机游走/比力白噪声;(b表示b系投影、wb表示白噪声) -
陀螺标定误差矩阵
dKg;加表标定误差矩阵dKa;(d表示陀螺、a表示加速度计) -
IMU误差结构体
imuerr,包含较多成员,可见imuerrset函数。
参考:严恭敏老师PSINS工具箱解读——imuerrset
function imuerr = imuerrset(eb, db, web, wdb, sqrtR0G, TauG, sqrtR0A, TauA, dKGii, dKAii, dKGij, dKAij, KA2, rxyz, dtGA)
% SIMU errors setting, including gyro & acc bias, noise and installation errors, etc.
%
% Prototype: imuerr = imuerrset(eb, db, web, wdb, sqrtR0G, TauG, sqrtR0A, TauA, dKGii, dKAii, dKGij, dKAij, KA2, rxyz, dtGA)
% Inputs: including information as follows 陀螺常值零偏,单位:度/小时
% eb - gyro constant bias (deg/h) 加速度计常值零偏,单位:微g
% db - acc constant bias (ug) 角度随机游走,单位:度/根号小时
% web - angular random walk (deg/sqrt(h)) 速度随机游走,单位:微g/根号赫兹
% wdb - velocity random walk (ug/sqrt(Hz)) 陀螺相关零偏,单位:度/小时
% sqrtR0G,TauG - gyro correlated bias, sqrtR0G in deg/h and TauG in s
% sqrtR0A,TauA - acc correlated bias, sqrtR0A in ug and TauA in s
% dKGii - gyro scale factor error (ppm) 陀螺尺度因子误差,单位:百万分之一
% dKAii - acc scale factor error (ppm) 加速度计尺度因子误差,单位:百万分之一
% dKGij - gyro installation error (arcsec) 陀螺安装误差角,单位:弧秒
% dKAij - acc installation error (arcsec) 加速度计安装误差角,单位:弧秒
% KA2 - acc quadratic coefficient (ug/g^2) 加速度计二次系数,单位:微g/g平方
% where,
% |dKGii(1) dKGij(4) dKGij(5)| |dKAii(1) 0 0 | 陀螺和加速度计的标定刻度误差
% dKg = |dKGij(1) dKGii(2) dKGij(6)| , dKa = |dKAij(1) dKAii(2) 0 |
% |dKGij(2) dKGij(3) dKGii(3)| |dKAij(2) dKAij(3) dKAii(3)|
% rxyz - acc inner-lever-arm, =[rx;ry;rz] (cm) 加速度计内杠杆臂,单位:厘米
% dtGA - time-asynchrony between gyro & acc, dtGA=Tacc_later-Tgyro_early>0 (ms) 陀螺和加速度计采样时刻未对准误差,单位:毫秒
% Output: imuerr - SIMU error structure array
%
% Example: 惯性级惯导的经典误差设置
% For inertial grade SIMU, typical errors are:
% eb=0.01dph, db=50ug, web=0.001dpsh, wdb=10ugpsHz
% scale factor error=10ppm, askew installation error=10arcsec
% sqrtR0G=0.001dph, taug=1000s, sqrtR0A=10ug, taug=1000s
% then call this funcion by
% imuerr = imuerrset(0.01,100,0.001,10, 0.001,1000,10,1000, 10,10,10,10, 10, 10, 10);
%
% See also imuadderr, gabias, avperrset, insinit, kfinit.
% Copyright(c) 2009-2014, by Gongmin Yan, All rights reserved.
% Northwestern Polytechnical University, Xi An, P.R.China
% 11/09/2013, 06/03/2014, 15/02/2015, 22/08/2015, 17/08/2016, 24/07/2020
global glv
if nargin==1 % for specific defined case
switch eb % 只输入一个参数eb,eb应为1或2,采用严老师设置的惯性级imu误差
case 1, imuerr = imuerrset(0.01, 100, 0.001, 10);
case 2, imuerr = imuerrset(0.01,100,0.001,10, 0.001,300,10,300, 10,10,10,10, 10, 2, 1);
end
return;
end
o31 = zeros(3,1); o33 = zeros(3);
% 设置imu误差结构体,对未输入变量设置默认值
imuerr = struct('eb',o31, 'db',o31, 'web',o31, 'wdb',o31,...
'sqg',o31, 'taug',inf(3,1), 'sqa',o31, 'taua',inf(3,1), 'dKg',o33, 'dKa',o33, 'dKga',zeros(15,1),'KA2',o31);
%% constant bias & random walk 陀螺和加速度计的常值零偏和随机游走
if ~exist('web', 'var'), web=0; end % 如果未输入角度随机游走,则设置其为0
if ~exist('wdb', 'var'), wdb=0; end % 如果未输入速度随机游走,则设置其为0
if length(eb)==2, eb=[eb(1);eb(1);eb(2)]; end
if length(db)==2, db=[db(1);db(1);db(2)]; end
if length(web)==2, web=[web(1);web(1);web(2)]; end
if length(wdb)==2, wdb=[wdb(1);wdb(1);wdb(2)]; end
% 转化成国际标准单位
imuerr.eb(1:3) = eb*glv.dph; imuerr.web(1:3) = web*glv.dpsh;
imuerr.db(1:3) = db*glv.ug; imuerr.wdb(1:3) = wdb*glv.ugpsHz;
%% correlated bias 陀螺和加速度计的相关零偏
if exist('sqrtR0G', 'var')
if TauG(1)==inf, imuerr.sqg(1:3) = sqrtR0G*glv.dphpsh; % algular rate random walk !!! 如果陀螺相关时间无穷大,陀螺零偏建模成随机游走
elseif TauG(1)>0, imuerr.sqg(1:3) = sqrtR0G*glv.dph.*sqrt(2./TauG); imuerr.taug(1:3) = TauG; % Markov process 如果陀螺相关时间大于0,陀螺零偏建模成马尔可夫过程
end
end
if exist('sqrtR0A', 'var')
if TauA(1)==inf, imuerr.sqa(1:3) = sqrtR0A*glv.ugpsh; % specific force random walk !!! 如果加速度计相关时间无穷大,加速度计零偏建模成随机游走
elseif TauA(1)>0, imuerr.sqa(1:3) = sqrtR0A*glv.ug.*sqrt(2./TauA); imuerr.taua(1:3) = TauA; % Markov process 如果加速度计相关时间大于0,加速度计零偏建模成马尔可夫过程
end
end
%% scale factor error 陀螺和加速度计的尺度因子误差
if exist('dKGii', 'var')
imuerr.dKg = setdiag(imuerr.dKg, dKGii*glv.ppm); % 将陀螺尺度因子误差赋值予陀螺标定刻度误差的对角线元素
end
if exist('dKAii', 'var')
imuerr.dKa = setdiag(imuerr.dKa, dKAii*glv.ppm);
end
%% installation angle error
if exist('dKGij', 'var') % 将陀螺安装误差角赋值予陀螺标定刻度误差的非对角线元素
dKGij = ones(6,1).*dKGij*glv.sec;
imuerr.dKg(2,1) = dKGij(1); imuerr.dKg(3,1) = dKGij(2); imuerr.dKg(3,2) = dKGij(3);
imuerr.dKg(1,2) = dKGij(4); imuerr.dKg(1,3) = dKGij(5); imuerr.dKg(2,3) = dKGij(6);
end
if exist('dKAij', 'var') % 将陀螺安装误差角赋值予陀螺标定刻度误差的非对角线元素
dKAij = ones(3,1).*dKAij*glv.sec;
imuerr.dKa(2,1) = dKAij(1); imuerr.dKa(3,1) = dKAij(2); imuerr.dKa(3,2) = dKAij(3);
end
imuerr.dKga = [imuerr.dKg(:,1); imuerr.dKg(:,2); imuerr.dKg(:,3);
imuerr.dKa(:,1); imuerr.dKa(2:3,2); imuerr.dKa(3,3)];
%% acc 2nd scale factor error 加速度计比例因子误差的二阶项
if exist('KA2', 'var')
imuerr.KA2(1:3) = KA2*glv.ugpg2;
end
%% acc inner-lever-arm error 加速度计的内杠杆臂误差
if exist('rxyz', 'var')
if length(rxyz)==1, rxyz(1:6)=rxyz; end
if length(rxyz)==6, rxyz(7:9)=[0;0;0]; end
imuerr.rx = rxyz(1:3)/100; imuerr.ry = rxyz(4:6)/100; imuerr.rz = rxyz(7:9)/100;
end
%% time-asynchrony between gyro & acc 陀螺和加速度计采样时刻未对准误差
if exist('dtGA', 'var')
imuerr.dtGA = dtGA/1000; % dtGA>0,加速度计采样滞后陀螺
end
7、其它常用变量
1.角速率 wnie
角速率
ω
i
e
n
\omega^n_{ie}
ωien 即
e
e
e 系相对于
i
i
i 系的角速度在
n
n
n 系的投影。wnin和wnen等变量符号类似,表示
ω
i
n
n
\omega^n_{in}
ωinn、
ω
e
n
n
\omega^n_{en}
ωenn
2. 不可交换误差补偿 phim/dvbm
陀螺角增量经不可交换误差补偿后的等效旋转矢量 ϕ m \phi_m ϕm
m − 1 m-1 m−1 到 m m m 时间段比力速度增量,经过不可交换误差补偿后的比力速度增量 Δ V m b \Delta V_m^b ΔVmb
3.重力矢量 gn
当地重力矢量gn=[0;0;-g],n表示
n
n
n 系下投影,g为重力大小
4.有害加速度 gcc
有害加速度,两个c,一个表示哥氏,一个表示向心力
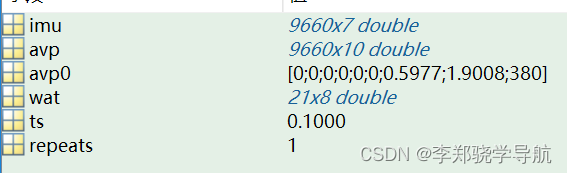
5.仿真轨迹结构体 trj
仿真轨迹结构体,存仿真中得到的avg、imu等参数,参见base1文件夹中的trjsimu函数:
global glv
if nargin<4, repeats = 1; end
wat1 = repmat(wat, repeats, 1);
% 设置初始参数:位置、姿态、地球参数
damping = 1-exp(-ts/5.0); % damping=0;
att = avp0(1:3); vn = avp0(4:6); pos = avp0(7:9);
eth = earth(pos, vn); Cbn_1 = a2mat(att)'; wm_1 = [0;0;0]; ts2 = ts/2;
% Mpv = [0, 1/eth.RMh, 0; 1/eth.clRNh, 0, 0; 0, 0, 1];
len = fix(sum(wat1(:,1))/ts);
[imu, avp] = prealloc(len, 7, 10);
ki = timebar(1, len, 'Trajectory Simulation.');
for k=1:size(wat1,1)
lenk = round(wat1(k,1)/ts); % the lenght at k phase K时段的长度
wt = wat1(k,3:5)'; at = wat1(k,6:8)'; % 当前时刻角速率、加速度
% 设置匀速运动ufflag、计算导航系参考速度
ufflag = 0;
if norm(wt)==0 && norm(at)==0 % uniform phase flag
ufflag = 1;
vnr = a2mat(att)*[0;wat1(k,2);0]; % velocity damping reference
end
for j=1:lenk
% 计算Cnt,将前向速度通过航向角、俯仰角转到导航系
sa = sin(att); ca = cos(att);
si = sa(1); sk = sa(3); ci = ca(1); ck = ca(3);
Cnt = [ ck, -ci*sk, si*sk;
sk, ci*ck, -si*ck;
0, si, ci ];
% 计算当前时刻姿态及 b->n 旋转矩阵
att = att + wt*ts;
Cnb = a2mat(att); % attitude
if ufflag==1 % damping
na = norm(vn-vnr)/ts; maxa = 0.1;
if na<maxa, na=maxa; end % max an is limited to maxa/(m/s^2)
vn1 = vn-damping/na*(vn-vnr); an = (vn1-vn)/ts;
vn01 = (vn+vn1)/2; vn = vn1;
else
an = Cnt*at;
vn1 = vn + an*ts; vn01 = (vn+vn1)/2; vn = vn1; % velocity
end
% 根据平均速度更新位置
dpos01 = [vn01(2)/eth.RMh;vn01(1)/eth.clRNh;vn01(3)]*ts2;
eth = earth(pos+dpos01, vn01);
pos = pos+dpos01*2; % position
% eth = earth(pos+Mpv*vn01*ts2, vn01);
% Mpv = [0, 1/eth.RMh, 0; 1/eth.clRNh, 0, 0; 0, 0, 1];
% pos = pos+Mpv*vn01*ts; % position
% 更新陀螺输出wm
phim = m2rv(Cbn_1*Cnb) + (Cbn_1+Cnb')*(eth.wnin*ts2);
% wm = phim;
wm = (glv.I33+askew(wm_1/12))^-1*phim; % gyro increment
% wm = (glv.I33-askew(wm_1/12))*phim; % gyro increment
% dvbm = Cbn_1*qmulv(rv2q(eth.wnin*ts2), (an-eth.gcc)*ts);
% 更新加速度输出vm
dvbm = Cbn_1*(rv2m(eth.wnin*ts2)*(an-eth.gcc)*ts);
vm = (glv.I33+askew(wm/2))^-1*dvbm; % acc increment
% vm = (glv.I33-askew(wm/2))*dvbm; % acc increment
kts = ki*ts;
avp(ki,:) = [att; vn; pos; kts]';
imu(ki,:) = [wm; vm; kts]';
wm_1 = wm; Cbn_1 = Cnb';
ki = timebar;
end
end
avp(ki:end,:) = []; imu(ki:end,:) = [];
avp = iatt2c(avp);
trj = varpack(imu, avp, avp0, wat, ts, repeats);
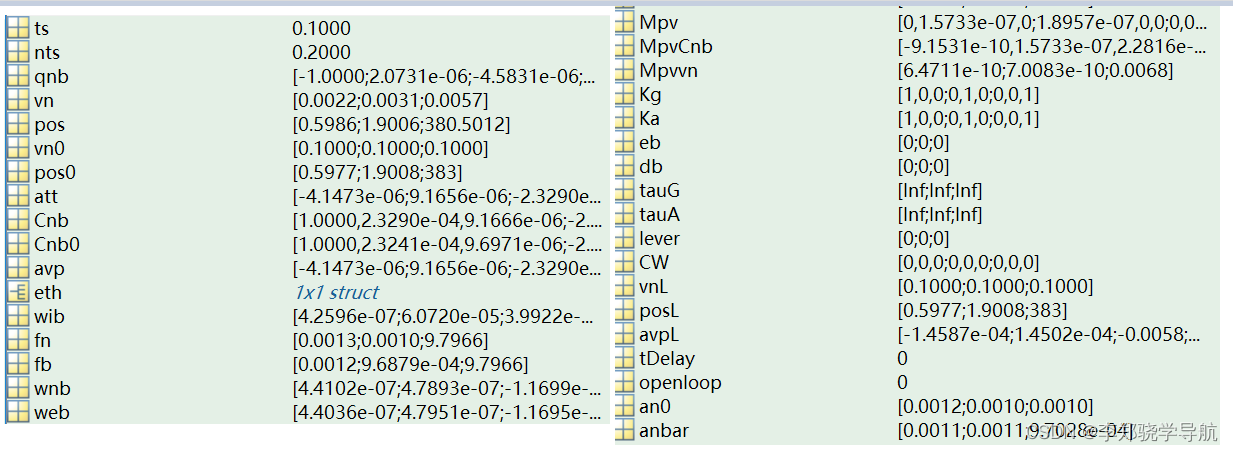
6.指北方位捷联导航解算结构体 ins
指北方位捷联导航解算结构体,参见base1文件夹中的insinit函数:
function ins = insinit(avp0, ts, var1, var2)
% SINS structure array initialization.
%
% Prototype: ins = insinit(avp0, ts, var1, var2)
% Initialization usages(maybe one of the following methods):
% ins = insinit(avp0, ts);
% ins = insinit(avp0, ts, avperr);
% ins = insinit(qnb0, vn0, pos0, ts);
% Inputs: avp0 - initial avp0 = [att0; vn0; pos0]
% ts - SIMU sampling interval
% avperr - avp error setting
% Output: ins - SINS structure array
%
% See also insupdate, avpset, kfinit.
% Copyright(c) 2009-2014, by Gongmin Yan, All rights reserved.
% Northwestern Polytechnical University, Xi An, P.R.China
% 22/03/2008, 12/01/2013, 18/03/2014
global glv
avp0 = avp0(:);
if length(avp0)==1, avp0=zeros(9,1); end % ins = insinit(0, ts);
if length(avp0)==4, avp0=[0;0;avp0(1); 0;0;0; avp0(2:4)]; end % ins = insinit([yaw;pos], ts);
if length(avp0)==6, avp0=[avp0(1:3); 0;0;0; avp0(4:6)]; end % ins = insinit([att;pos], ts);
if length(avp0)==7, avp0=[0;0;avp0]; end % ins = insinit([yaw;vn;pos], ts);
if nargin==2 % ins = insinit(avp0, ts);
[qnb0, vn0, pos0] = setvals(a2qua(avp0(1:3)), avp0(4:6), avp0(7:9));
elseif nargin==3 % ins = insinit(avp0, ts, avperr);
avperr = var1;
avp0 = avpadderr(avp0, avperr);
[qnb0, vn0, pos0] = setvals(a2qua(avp0(1:3)), avp0(4:6), avp0(7:9));
elseif nargin==4 % ins = insinit(qnb0, vn0, pos0, ts);
[qnb0, vn0, pos0, ts] = setvals(avp0, ts, var1, var2);
end
ins = [];
ins.ts = ts; ins.nts = 2*ts;
[ins.qnb, ins.vn, ins.pos] = setvals(qnb0, vn0, pos0); ins.vn0 = vn0; ins.pos0 = pos0;
[ins.qnb, ins.att, ins.Cnb] = attsyn(ins.qnb); ins.Cnb0 = ins.Cnb;
ins.avp = [ins.att; ins.vn; ins.pos];
ins.eth = ethinit(ins.pos, ins.vn);
% 'wib,web,fn,an,Mpv,MpvCnb,Mpvvn,CW' may be very useful outside SINS,
% so we calucate and save them.
ins.wib = ins.Cnb'*ins.eth.wnin;
ins.fn = -ins.eth.gn; ins.fb = ins.Cnb'*ins.fn;
[ins.wnb, ins.web, ins.an] = setvals(zeros(3,1));
ins.Mpv = [0, 1/ins.eth.RMh, 0; 1/ins.eth.clRNh, 0, 0; 0, 0, 1];
ins.MpvCnb = ins.Mpv*ins.Cnb; ins.Mpvvn = ins.Mpv*ins.vn;
[ins.Kg, ins.Ka] = setvals(eye(3)); % calibration parameters
[ins.eb, ins.db] = setvals(zeros(3,1));
[ins.tauG, ins.tauA] = setvals(inf(3,1)); % gyro & acc correlation time
ins.lever = zeros(3,1); ins = inslever(ins); % lever arm
ins.tDelay = 0; % time delay
ins.openloop = 0;
glv.wm_1 = zeros(3,1)'; glv.vm_1 = zeros(3,1)'; % for 'single sample+previous sample' coning algorithm
ins.an0 = zeros(3,1); ins.anbar = ins.an0;
7.导航地球相关计算结构体 eth
导航地球相关计算结构体,参见base1文件夹中的ethinit函数:
function eth = ethinit(pos, vn)
% The Earth related parameters (structure array) initialization.
%
% Prototype: eth = ethinit(pos, vn)
% Inputs: pos - geographic position [lat;lon;hgt]
% vn - velocity
% Outputs: eth - parameter structure array
%
% See also ethupdate, earth.
% Copyright(c) 2009-2014, by Gongmin Yan, All rights reserved.
% Northwestern Polytechnical University, Xi An, P.R.China
% 23/05/2014
global glv
if nargin<2, vn = [0; 0; 0]; end
if nargin<1, pos = [0; 0; 0]; end
eth.Re = glv.Re; eth.e2 = glv.e2; eth.wie = glv.wie; eth.g0 = glv.g0;
eth = ethupdate(eth, pos, vn);
eth.wnie = eth.wnie(:); eth.wnen = eth.wnen(:);
eth.wnin = eth.wnin(:); eth.wnien = eth.wnien(:);
eth.gn = eth.gn(:); eth.gcc = eth.gcc(:);

8.Kalman滤波结构体 kf
Kalman滤波结构体,会根据定义的维数psinsdef进行对应的初始化,参见kf文件夹中的kfinit函数:
function kf = kfinit(ins, varargin)
% Kalman filter initializes for structure array 'kf', this precedure
% usually includs the setting of structure fields: Qt, Rk, Pxk, Hk.
%
% Prototype: kf = kfinit(ins, varargin)
% Inputs: ins - SINS structure array, if not struct then nts=ins;
% varargin - if any other parameters
% Output: kf - Kalman filter structure array
%
% See also kfinit0, kfsetting, kffk, kfkk, kfupdate, kffeedback, psinstypedef.
% Copyright(c) 2009-2014, by Gongmin Yan, All rights reserved.
% Northwestern Polytechnical University, Xi An, P.R.China
% 09/10/2013
global glv psinsdef
[Re,deg,dph,ug,mg] = ... % just for short
setvals(glv.Re,glv.deg,glv.dph,glv.ug,glv.mg);
o33 = zeros(3); I33 = eye(3);
kf = [];
if isstruct(ins), nts = ins.nts;
else nts = ins;
end
switch(psinsdef.kfinit)
case psinsdef.kfinit153,
psinsdef.kffk = 15; psinsdef.kfhk = 153; psinsdef.kfplot = 15;
[davp, imuerr, rk] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; zeros(9,1)])^2;
kf.Rk = diag(rk)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db]*1.0)^2;
kf.Hk = kfhk(0);
case psinsdef.kfinit156,
psinsdef.kffk = 15; psinsdef.kfhk = 156; psinsdef.kfplot = 15;
[davp, imuerr, rk] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; zeros(9,1)])^2;
kf.Rk = diag(rk)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db]*1.0)^2;
kf.Hk = kfhk(0);
case psinsdef.kfinit183,
psinsdef.kffk = 18; psinsdef.kfhk = 183; psinsdef.kfplot = 18;
[davp, imuerr, lever, r0] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; zeros(9+3,1)])^2;
kf.Rk = diag(r0)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db; lever]*1.0)^2;
kf.Hk = zeros(3,18);
case psinsdef.kfinit186,
psinsdef.kffk = 18; psinsdef.kfhk = 186; psinsdef.kfplot = 18;
[davp, imuerr, lever, r0] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; zeros(3,1); imuerr.sqg; imuerr.sqa; zeros(3,1)])^2;
kf.Rk = diag(r0)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db; lever]*1.0)^2;
kf.Hk = zeros(6,18);
case psinsdef.kfinit193
psinsdef.kffk = 19; psinsdef.kfhk = 193; psinsdef.kfplot = 19;
[davp, imuerr, lever, dT, r0] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; [1/Re;1/Re;1]*glv.mpsh; ...
[1;1;1]*0*glv.dphpsh; [1;1;1]*0*glv.ugpsh; [1;1;1]*0.*glv.mpsh; 0])^2;
kf.Rk = diag(r0)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db; lever; dT]*1.0)^2;
kf.Hk = zeros(3,19);
case psinsdef.kfinit196
psinsdef.kffk = 19; psinsdef.kfhk = 196; psinsdef.kfplot = 19;
[davp, imuerr, lever, dT, r0] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; [1/Re;1/Re;1]*0*glv.mpsh; ...
[1;1;1]*0*glv.dphpsh; [1;1;1]*0*glv.ugpsh; [1;1;1]*0*glv.mpsh; 0])^2;
kf.Rk = diag(r0)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db; lever; dT]*1.0)^2;
kf.Hk = zeros(6,19);
case psinsdef.kfinit246
psinsdef.kffk = 24; psinsdef.kfhk = 246; psinsdef.kfplot = 24;
[davp, imuerr, r0] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; [1/Re;1/Re;1]*0*glv.mpsh; ...
[1;1;1]*0*glv.dphpsh; [1;1;1]*0*glv.ugpsh; zeros(9,1)])^2;
kf.Rk = diag(r0)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db; imuerr.dKga(1:9)]*1.0)^2;
kf.Hk = zeros(6,24);
case psinsdef.kfinit331,
psinsdef.kffk = 33; psinsdef.kfhk = 331; psinsdef.kfplot = 33;
[davp, imuerr, r0] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; zeros(9+15+3,1)])^2;
kf.Rk = diag(r0)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db; imuerr.dKga; imuerr.KA2])^2;
kf.Hk = kfhk(ins);
kf.xtau(1:psinsdef.kffk,1) = 0;
case psinsdef.kfinit346,
psinsdef.kffk = 34; psinsdef.kfhk = 346; psinsdef.kfplot = 34;
[davp, imuerr, lever, dT, r0] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; zeros(9+3+1+15,1)])^2;
kf.Rk = diag(r0)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db; lever; dT; imuerr.dKga])^2;
kf.Hk = kfhk(ins);
kf.xtau(1:psinsdef.kffk,1) = 0;
case psinsdef.kfinit376,
psinsdef.kffk = 37; psinsdef.kfhk = 376; psinsdef.kfplot = 37;
[davp, imuerr, lever, dT, r0] = setvals(varargin);
kf.Qt = diag([imuerr.web; imuerr.wdb; zeros(9+3+1+15+3,1)])^2;
kf.Rk = diag(r0)^2;
kf.Pxk = diag([davp; imuerr.eb; imuerr.db; lever; dT; imuerr.dKga; davp(4:6)]*10)^2;
kf.Hk = kfhk(ins);
kf.xtau(1:psinsdef.kffk,1) = 0;
otherwise,
kf = feval(psinsdef.typestr, psinsdef.kfinittag, [{ins},varargin]);
end
kf = kfinit0(kf, nts);

五、数据导入、转换
- 二进制(纯double型)格式文件,使用
binfile函数,这对导入C语言生成的数据文件快速方便;或者可参照binfile,使用fread自行编程导入特定格式的二进制文件; - 文本文件/或
.mat格式文件,使用Matlab的load或importdata函数;mat是MATLAB专用的数据文件,有压缩,很方便MATLAB之间存数据,但C语言中没法读。 - 特殊格式的PSINS-IMU/AVP文件,可用
imufile、avpfile等函数。
从文件直接导入Matlab工作空间的数据通常是一个二维数组,其各列顺序及量纲单位不一定符合PSINS的习惯,需再进行数据提取和转换:
- 使用
imuidx提取IMU数据并进行单位转换,陀螺为角增量、加表为速度增量;如需要,还可借助于imurfu函数将IMU转换至右-前-上坐标系; - 使用
avpidx提取AVP数据并进行单位转换,结果姿态/纬经为弧度、方位角北偏西为正; - 使用
gpsidx提取GNSS速度/定位数据并进行单位转换,纬经度为弧度;通常GNSS的频率低于IMU频率,为删除重复数据行可调用norep函数;为删除数据为0行可调用no0函数; - 使用
tshift或adddt函数可将数据的起始时间转换至指定的相对时间。一般用相对时间而不用周内秒,周内秒数值太大了,看着不方便。
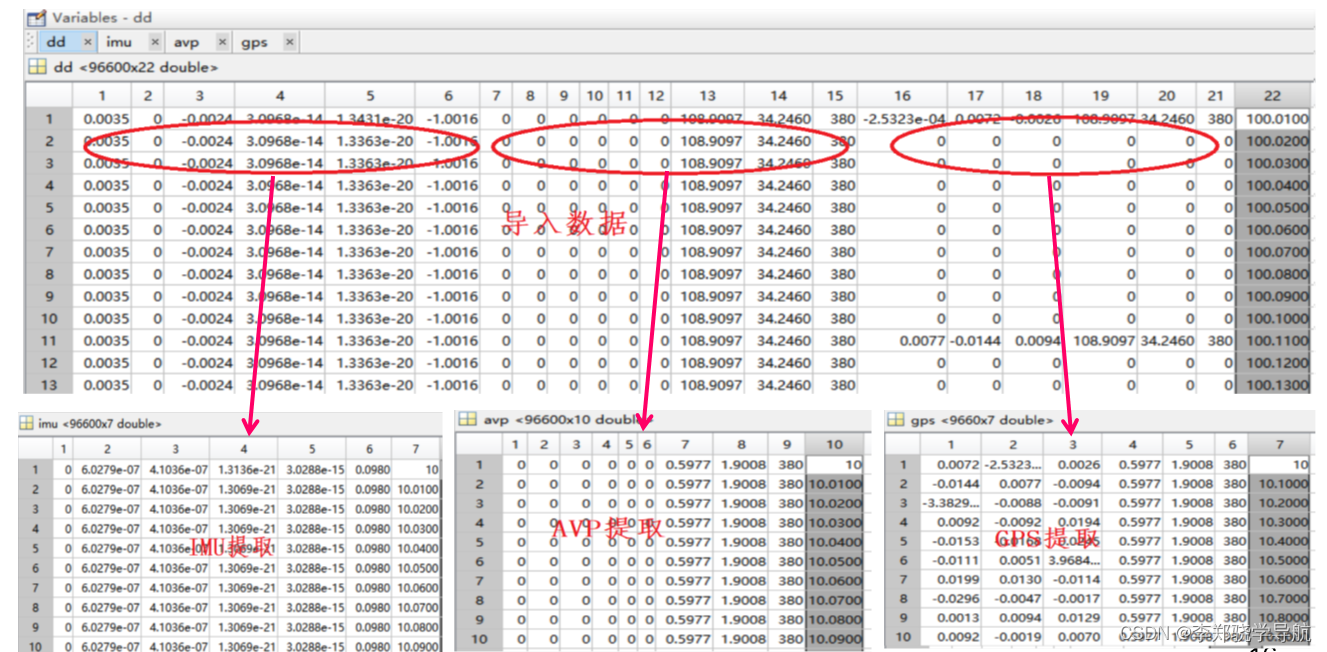
参考test_IMUAVPGPS_extract_trans.m脚本文件,代码和效果图如下:
dd = binfile('imuavpgps.bin', 22);
open dd;
imu = imurfu(imuidx(dd, [1:6,22],glv.dps,glv.g0,trj.ts),'frd');
avp = avpidx(dd,[7:12,14,13,15,22],1,1);
gps = gpsidx(dd,[17,16,-18,20,19,21,22],1);
[imu,avp,gps] = tshift(imu,avp,gps,10);
六、绘图显示
1、绘图辅助函数
-
myfig:创建图窗,有两种用法:myfig()、myfig('图窗名')、myfig('图窗名','纵坐标标签'):调用myfigure创建一个画图窗口,绘制白底全屏图(MATLAB直接画是灰底没全屏的),传回图窗句柄,可传入图窗名。当第一个参数是字符串时,第二个参数不起作用。myfig('绘图数据','纵坐标标签'):直接调用myfigure、plot、xygo绘图。
function h = myfig(namestr, ylb) if ~exist('namestr','var') h0 = myfigure; else % 如果传入第一个参数是用于绘图的数据,第二个参数是纵坐标标签,直接plot、xygo绘图 if ~ischar(namestr) % myfig(data, ylabel); if nargin<2, ylb='val'; end myfig; plot(namestr); xygo(ylb); return; end h = myfigure(namestr); end if nargout==1 % 如果要获取返回值,传回图窗句柄 h = h0; endfunction h = myfigure(namestr) scrsz = get(0,'ScreenSize'); % scrsz = [left, bottom, width, height] 获取屏幕分辨率 scrsz = [0.01*scrsz(3), 0.05*scrsz(4), 0.95*scrsz(3), 0.93*scrsz(4)]; % figure('Position',scrsz); if ~exist('namestr','var') namestr = 'PSINS Toolbox'; end h0 = figure('OuterPosition',scrsz, 'Name',namestr, 'Color','White'); % set(gcf, 'Color','White'); if nargout==1 % 如果要获取返回值,传回图窗句柄 h = h0; end -
xygo:启用网格(grid on)、给出坐标轴横纵标签(特殊标识由labeldef函数给出)。有三种用法:xygo():默认纵轴是value,默认横轴是时间txygo('纵轴标签'):传入纵轴标签,默认横轴是时间txygo('横轴标签','纵轴标签'):传入横轴标签、纵轴标签
function xygo(xtext, ytext) % 如果没传入参数,默认纵轴是 value,默认横轴是时间 t if nargin==0 % xygo ytext = 'value'; xtext = labeldef('t'); end % 如果传入一个参数,其做为纵轴标签,默认横轴是时间 t if nargin==1 % xygo(ytext) ytext = xtext; xtext = labeldef('t'); end % 如果传入两个参数,作为横轴、纵轴 xlabel(labeldef(xtext)); ylabel(labeldef(ytext)); grid on; hold on; -
labeldef:定义简化标签精以简代码,调用此函数可以将简化标签转为完整标签。其中specl_string结构体存着简化标签与完整标签的对应关系。如果传入的是t,根据所选时间刻度选择合适的时间单位。function stext = labeldef(stext) global glv global specl_string if isempty(specl_string) % 标签对应结构体,第一列为简洁标签,第二列为对应的完整形式 specl_string = {... % string cell 't/s' '\itt \rm / s'; 't/m' '\itt \rm / min'; 't/h' '\itt \rm / h'; 't/d' '\itt \rm / d'; 'phi', '\it\phi\rm / ( \prime )'; 'phiE', '\it\phi\rm_E / ( \prime\prime )'; 'phiN', '\it\phi\rm_N / ( \prime\prime )'; 'phiU', '\it\phi\rm_U / ( \prime )'; 'phiEN', '\it\phi\rm_E,\it\phi\rm_N / ( \prime\prime )'; 'phix', '\it\phi_x\rm / ( \circ )'; 'phiy', '\it\phi_y\rm / ( \circ )'; 'phiz', '\it\phi_z\rm / ( \circ )'; 'phixy', '\it\phi _{x,y}\rm / ( \circ )'; 'mu', '\it\mu \rm / ( \prime )'; 'mux', '\it\mu_x \rm / ( \prime )'; 'muy', '\it\mu_y \rm / ( \prime )'; 'muz', '\it\mu_z \rm / ( \prime )'; 'theta', '\it\theta \rm / ( \prime )'; 'dVEN', '\it\delta V \rm_{E,N} / ( m/s )'; 'dVE', '\delta\it V \rm_E / ( m/s )'; 'dVN', '\delta\it V \rm_N / ( m/s )'; 'dVU', '\delta\it V \rm_U / ( m/s )'; 'dV', '\delta\it V\rm / ( m/s )'; 'pr', '\it\theta , \gamma\rm / ( \circ )'; 'ry', '\it\gamma , \psi\rm / ( \circ )'; 'p', '\it\theta\rm / ( \circ )'; 'r', '\it\gamma\rm / ( \circ )'; 'y', '\it\psi\rm / ( \circ )'; 'att', '\itAtt\rm / ( \circ )'; 'datt', '\itdAtt\rm / ( \prime )'; 'VEN', '\itV \rm_{E,N} / ( m/s )'; 'VE', '\itV \rm_E / ( m/s )'; 'VN', '\itV \rm_N / ( m/s )'; 'VU', '\itV \rm_U / ( m/s )'; 'V', '\itV\rm / ( m/s )'; 'Vx', '\itVx\rm / ( m/s )'; 'Vy', '\itVy\rm / ( m/s )'; 'Vz', '\itVz\rm / ( m/s )'; 'dlat', '\delta\it L\rm / m'; 'dlon', '\delta\it \lambda\rm / m'; 'dH', '\delta\it H\rm / m'; 'dP', '\delta\it P\rm / m'; 'lat', '\itL\rm / ( \circ )'; 'lon', '\it\lambda\rm / ( \circ )'; 'hgt', '\ith\rm / ( m )'; 'xyz', 'XYZ / ( m )'; 'est', 'East\rm / m'; 'nth', 'North\rm / m'; 'H', '\itH\rm / m'; 'DP', '\Delta\it P\rm / m'; 'ebyz', '\it\epsilon _{y,z}\rm / ( (\circ)/h )'; 'eb', '\it\epsilon\rm / ( (\circ)/h )'; 'en', '\it\epsilon\rm / ( (\circ)/h )'; 'db', '\it\nabla\rm / \mu\itg'; 'dKij', '\delta\itKij\rm / (\prime\prime)'; 'dKii', '\delta\itKii\rm / ppm'; 'Ka2', 'Ka2 / ug/g^2'; 'dbU', '\it\nabla \rm_U / \mu\itg'; 'L', '\itLever\rm / m'; 'dT', '\delta\it T_{asyn}\rm / s'; 'dKgzz', '\delta\it Kgzz\rm / ppm'; 'dKg', '\delta\it Kg\rm / ppm'; 'dAg', '\delta\it Ag\rm / ( \prime\prime )'; 'dKa', '\delta\it Ka\rm / ppm'; 'dAa', '\delta\it Aa\rm / ( \prime\prime )'; 'wx', '\it\omega_x\rm / ( (\circ)/s )'; 'wy', '\it\omega_y\rm / ( (\circ)/s )'; 'wz', '\it\omega_z\rm / ( (\circ)/s )'; 'w', '\it\omega\rm / ( (\circ)/s )'; 'wxdph', '\it\omega_x\rm / ( (\circ)/h )'; 'wydph', '\it\omega_y\rm / ( (\circ)/h )'; 'wzdph', '\it\omega_z\rm / ( (\circ)/h )'; 'wdph', '\it\omega\rm / ( (\circ)/h )'; 'fx', '\itf_x\rm / \itg'; 'fy', '\itf_y\rm / \itg'; 'fz', '\itf_z\rm / \itg'; 'f', '\itf\rm / \itg'; 'fxug', '\itf_x\rm / u\itg'; 'fyug', '\itf_y\rm / u\itg'; 'fzug', '\itf_z\rm / u\itg'; 'fug', '\itf\rm / u\itg'; 'Temp', '\itT\rm / \circC'; 'frq', '\itf\rm / Hz'; 'dinst', '\delta\it\theta , \rm\delta\it\psi\rm / ( \prime )'; }; end % 如果传入的是t,根据glv.tscale(end)里时间的尺度,选择合适的选择合适的时间单位 if strcmp(stext,'t')==1 switch glv.tscale(end) case 1, stext='t/s'; case 60, stext='t/m'; case 3600, stext='t/h'; case 24*3600, stext='t/d'; end end % 遍历上面定义的 specl_string 结构体,如果 for k=1:length(specl_string) if strcmp(stext,specl_string(k,1))==1 stext = specl_string{k,2}; break; end end
2、传感器数据绘图
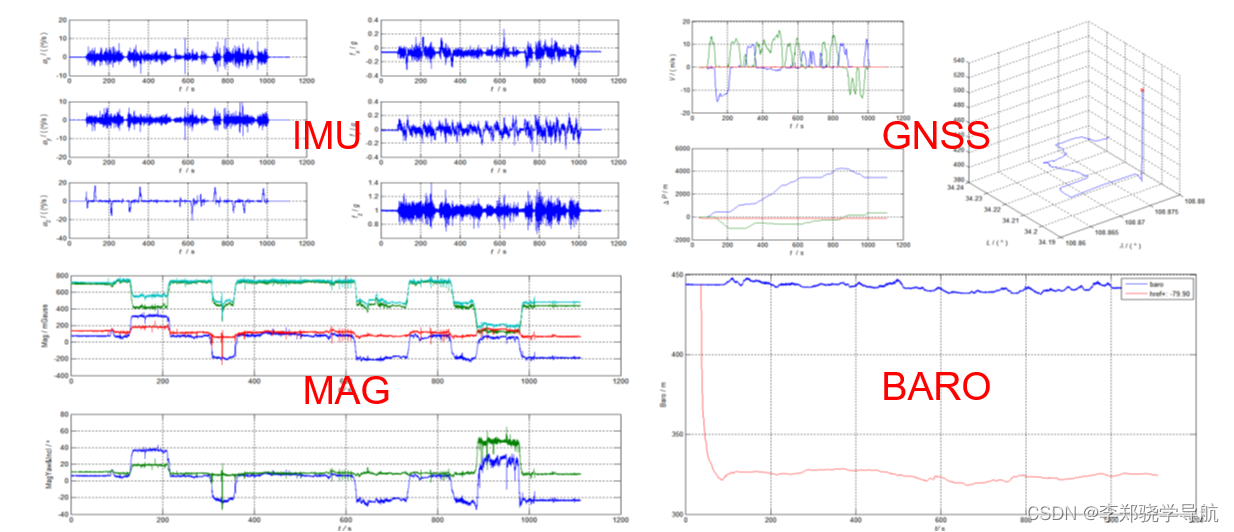
给传感器数据,直接画出上面的图,要写很多行代码,所以封装了一些函数:
-
imuplot、imumeanplot:IMU/平滑绘图,陀螺单位deg/s,加表单位g -
gpsplot:GNSS绘图,可同时包含速度和定位信息、或仅有定位信息。会做判断4列认为只有时间位置,7列认为时间位置速度 -
magplot:三轴地磁绘图,假设载体水平角为0,给出磁倾角/偏角 -
odplot/dvlplot:里程仪绘图(输入数据为路程增量,绘图显示为速度) -
baroplot:气压高度绘图,画压力对应的高度
3、导航结果绘图
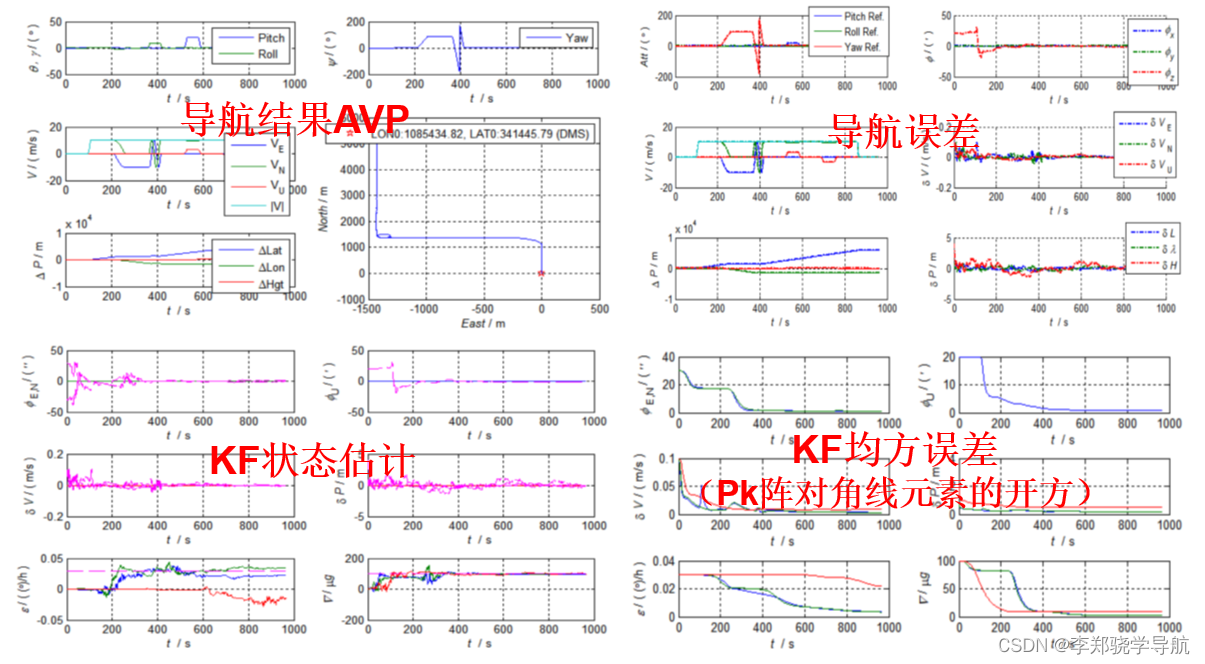
-
insplot:纯惯性导航结果AVP绘图,三个姿态、三个速度、三个位置,- 俯仰角、横滚角通常比方位角小,分开画会显示的全面一些。
- 位置就是位置的增量
- 速度是东北天三个方向,和模值
- 二维轨迹图,用相对坐标
-
inserrplot、avpcmpplot:导航误差 -
avpcmpplot:比较绘图;有参考基准时、或高精度惯导和低精度惯导、或GNSS和惯导 -
kfplot、xpplot:Kalman滤波结果状态或均方差阵对角线元素绘图。
4、进度条函数
timebar:直观显示程序循环运行进度情况、在程序循环运行过程中如人为点击Cancel按钮则进度条则报错中断程序。循环里每一次都调用,返回调用的次数tk,参数:
tStep:每一步运行步数tTotal:总步数msgstr:进度条上要显示的字符串

七、SINS/GPS组合导航仿真举例
本篇只是举个仿真的例子,之后的博客再做细致的解读。
1、生成仿真轨迹
参考博客:PSINS源码阅读—test_SINS_trj、严恭敏老师PSINS工具箱解读——trjfile、关于PSINS运动轨迹仿真模块的理解和思考、PSINS工具箱中轨迹生成工具详细解析
参考书:严老师硕士论文第五章、捷联惯导与组合导航第8章
运行demo\test_SINS_trj.m脚本,生成仿真轨迹
glvs % 主程序的第一行一般都是glvs,定义全局变量
ts = 0.1; % sampling interval 采样时间
avp0 = [[0;0;0]; [0;0;0]; glv.pos0]; % init avp 设置avp初始参数
% trajectory segment setting 分段设置轨迹剖面参数,由一段段线拼接而成
% uniform:保持运动状态、accelerate:加速、coturnleft:左转、deaccelerate:减速
xxx = [];
seg = trjsegment(xxx, 'init', 0); % 轨迹结构数组的初始化
seg = trjsegment(seg, 'uniform', 100); % 保持上一状态100s
seg = trjsegment(seg, 'accelerate', 10, xxx, 1); % 用1m/s2的速度加速10s
seg = trjsegment(seg, 'uniform', 100); % 保持上一时刻状态100s
seg = trjsegment(seg, 'coturnleft', 45, 2, xxx, 4); % 协调左转弯,先横滚方向左转4s,再整体转45s,最后横滚方向右转4s.考虑到了航向与横滚
seg = trjsegment(seg, 'uniform', 100); % 保持上一个状态100s
seg = trjsegment(seg, 'coturnright', 10*5, 9, xxx, 4); % 协调右转弯,先横滚方向右转4s,再整体转50s,最后横滚方向左转4s.考虑到了航向与横滚
seg = trjsegment(seg, 'uniform', 100); % 保持上一时刻状态100s
seg = trjsegment(seg, 'climb', 10, 2, xxx, 50); % 向上爬坡10s
seg = trjsegment(seg, 'uniform', 100); % 保持上一时刻状态100s
seg = trjsegment(seg, 'descent', 10, 2, xxx, 50); % 下降10s
seg = trjsegment(seg, 'uniform', 100); % 保持上一时刻状态100s
seg = trjsegment(seg, 'deaccelerate', 5, xxx, 2); % 减速5s
seg = trjsegment(seg, 'uniform', 100); % 保持上一时刻状态100s
% generate, save & plot
trj = trjsimu(avp0, seg.wat, ts, 1);
trjfile('trj10ms.mat', trj);
insplot(trj.avp);
imuplot(trj.imu);
轨迹参数图:
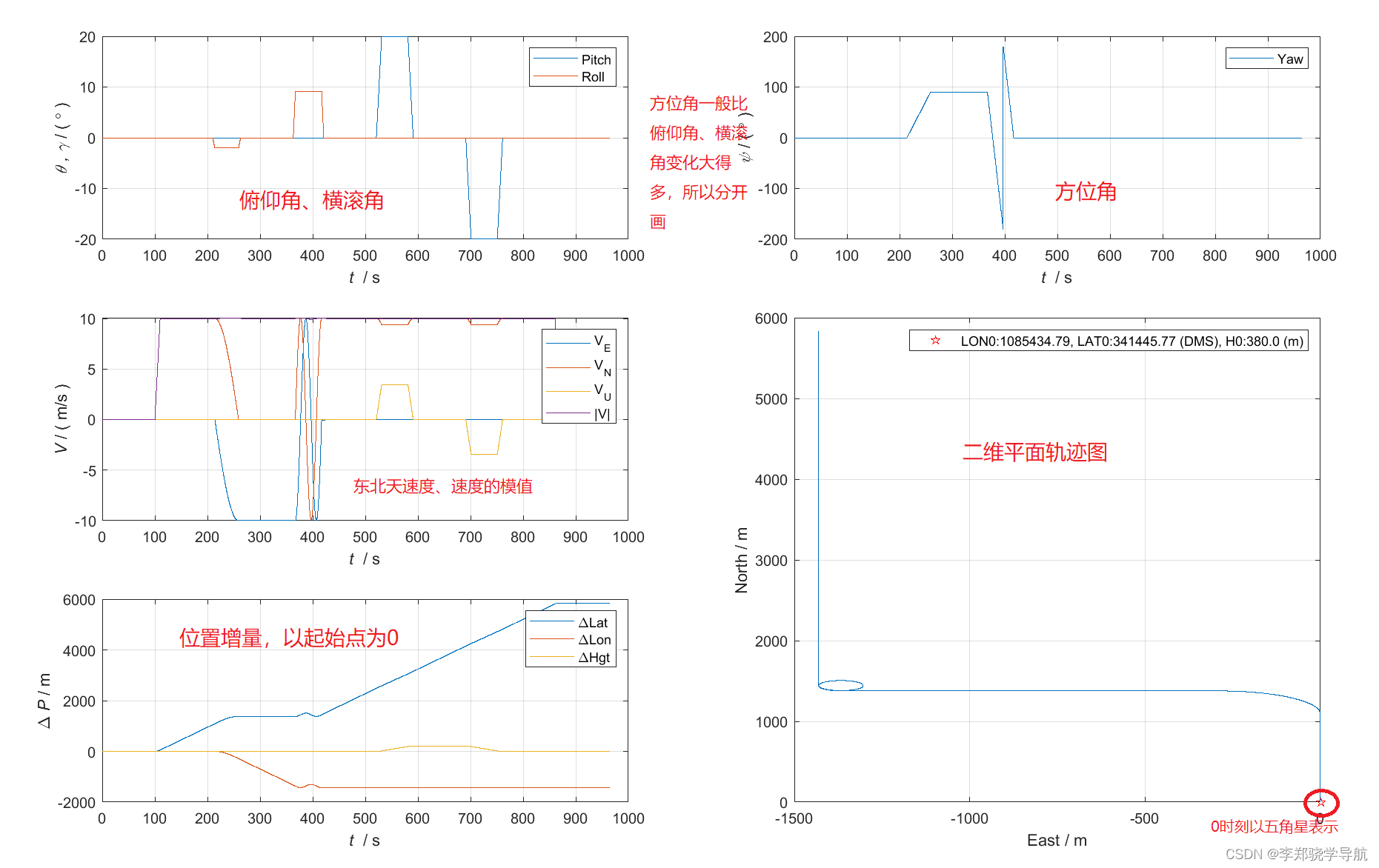
IMU参数图:左边是三个陀螺的输出,右边是三个比力的输出
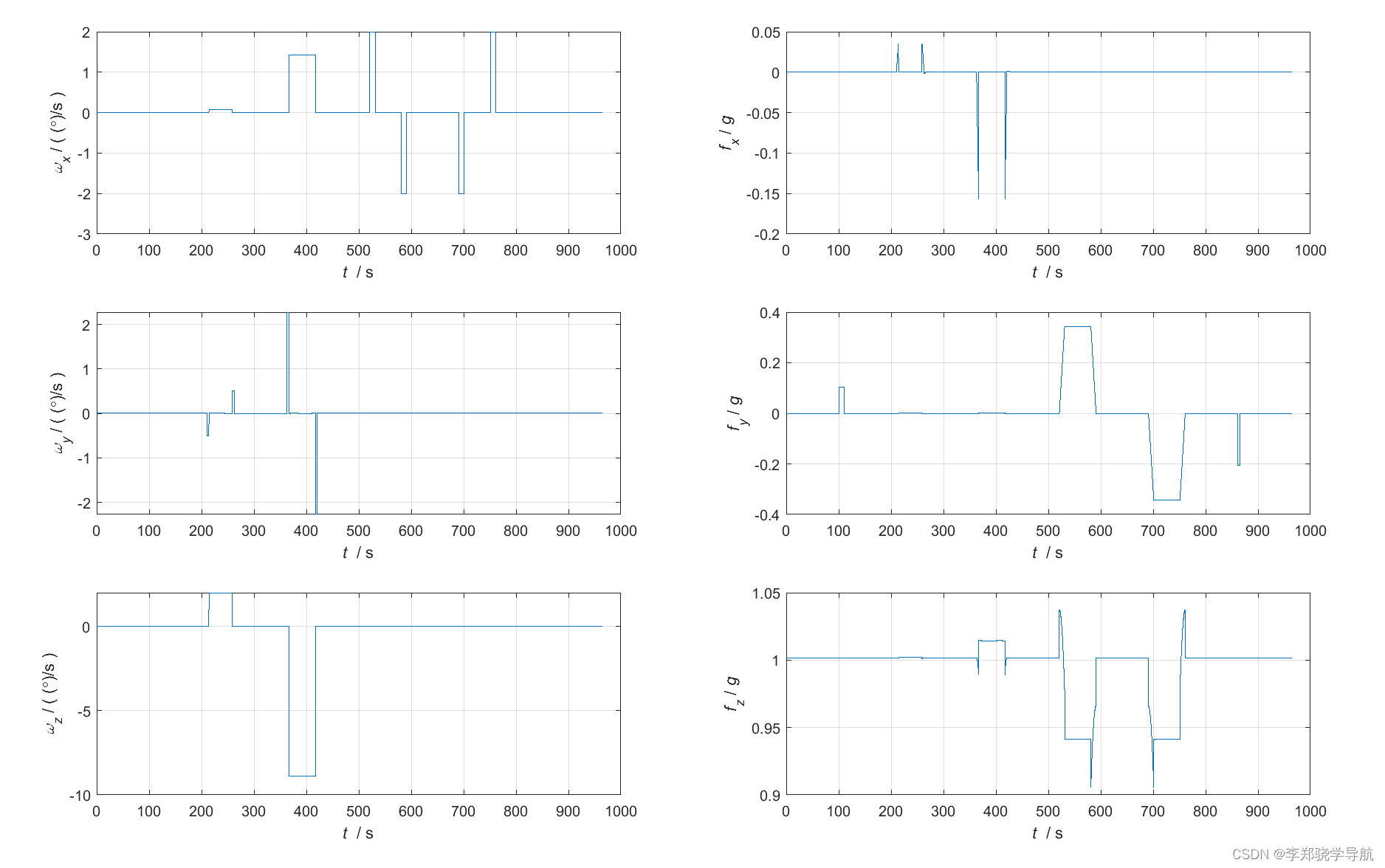
2、纯惯导仿真
运行demo\test_SINS.m脚本,纯惯导仿真
glvs
trj = trjfile('trj10ms.mat'); % 读轨迹
%% error setting 设置惯性器件误差和avp参数
imuerr = imuerrset(0.01, 100, 0.001, 10); % 陀螺漂移、零篇、加表随机游走、速度随机游走
imu = imuadderr(trj.imu, imuerr); % 往轨迹IMU中加上一步设置的误差
davp0 = avperrset([0.5;0.5;5], 0.1, [10;10;10]); % 失准角误差0.5/0.5/5、速度误差0.1m/s、位置误差等10m
avp00 = avpadderr(trj.avp0, davp0);
trj = bhsimu(trj, 1, 10, 3, trj.ts); % 气压高度计
%% pure inertial navigation & error plot 纯惯导解算作图
avp = inspure(imu, avp00, trj.bh, 1);
% avp = inspure(imu, avp00, 'f', 1);
avperr = avpcmpplot(trj.avp, avp); % 存惯导仿真结果与轨迹仿真结果比较作图
纯惯导仿真avp:可以看出到最后速度都不延北方向了
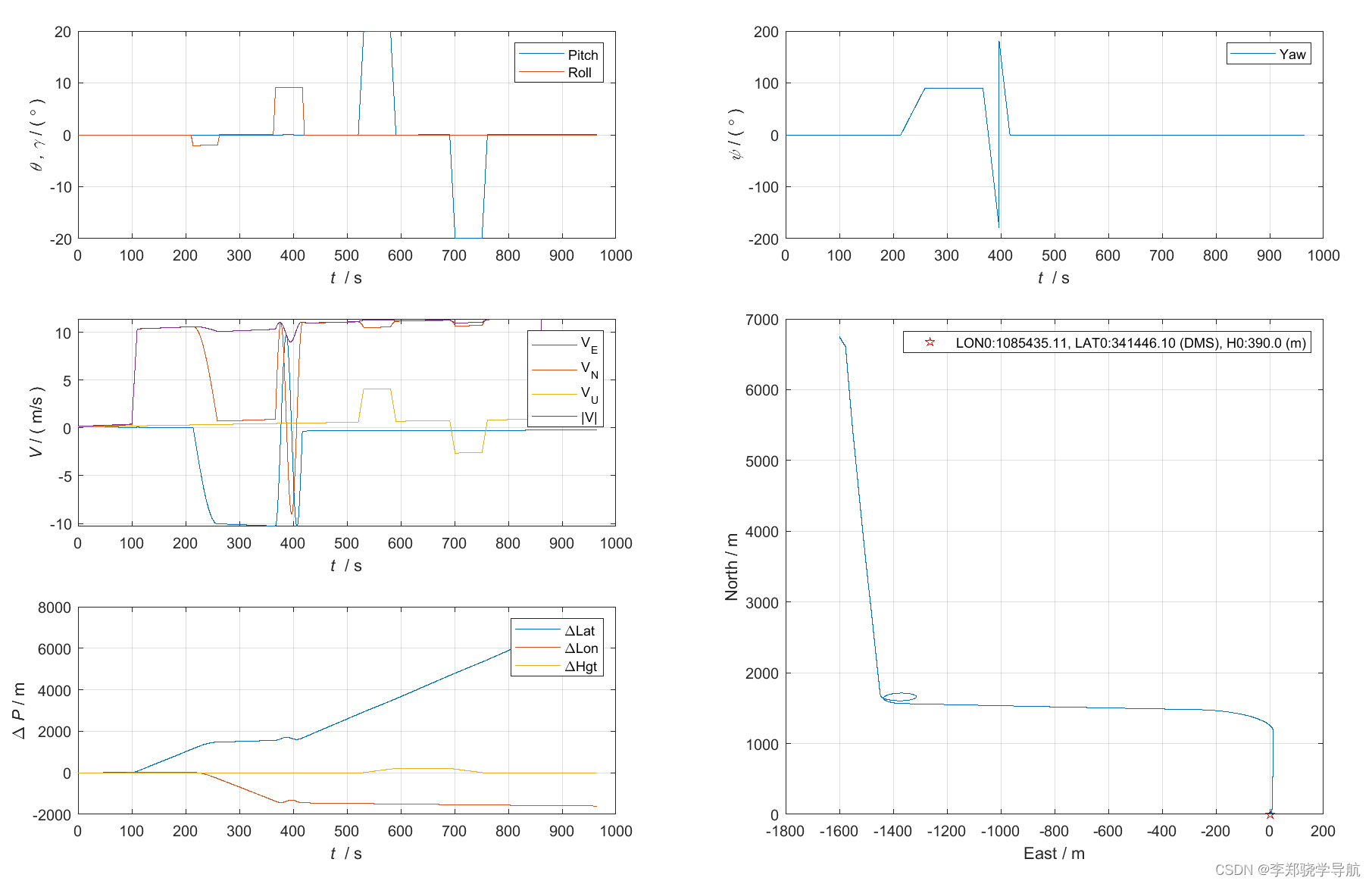
与真实轨迹比误差图:
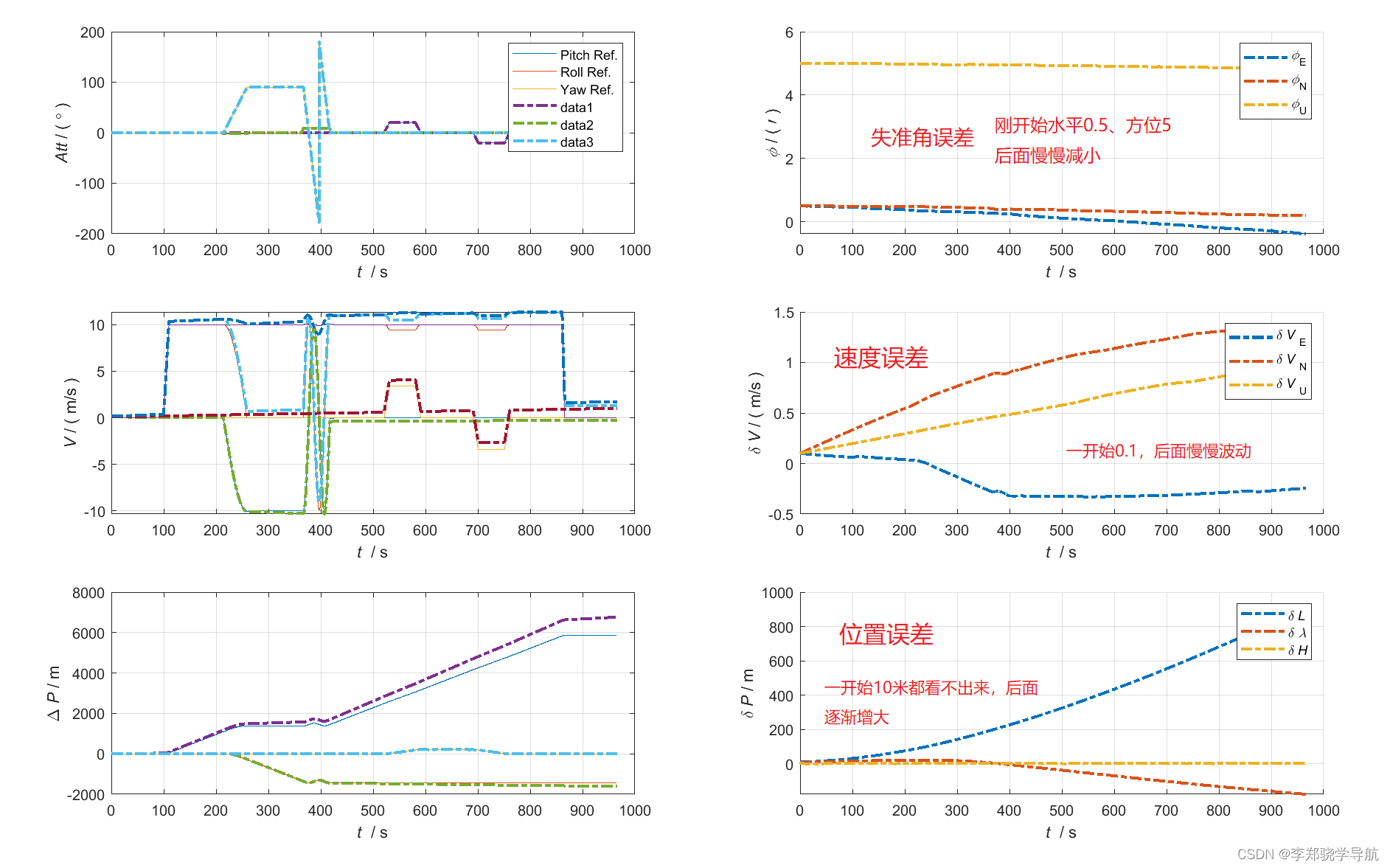
3、SINS-GPS仿真
参考:严恭敏老师PSINS工具箱解读——test_SINS_GPS_153
运行demo\test_SINS_GPS_153.m脚本,组合导航仿真,15维状态+3维量测、15维状态:三个失准角、三个速度误差、三个位置误差、三个陀螺漂移常值、三个加计零偏常值
glvs
psinstypedef(153); % 全局变量,主要设置状态转移矩阵的维数、量测矩阵的维数和画图
trj = trjfile('trj10ms.mat'); % 加载轨迹数据
% initial settings
[nn, ts, nts] = nnts(2, trj.ts); % 子样数和采样间隔
imuerr = imuerrset(0.03, 100, 0.001, 5); % imu误差,分别为陀螺常值零偏、加速度计常值零偏、角度随机游走和速度随机游走,请参考imuerrset函数解读
imu = imuadderr(trj.imu, imuerr); % 对参考imu数据添加误差生成实际imu测量值,请参考imuadderr解读
davp0 = avperrset([0.5;-0.5;20], 0.1, [1;1;3]); % 初始姿态、速度和位置误差,注意姿态的单位为:分,请参考avperrset函数解读
ins = insinit(avpadderr(trj.avp0,davp0), ts); % 对参考初始姿态、速度和位置添加误差,并进行惯导初始化用于后面更新
% KF filter
rk = poserrset([1;1;3]); % 位置量测噪声
kf = kfinit(ins, davp0, imuerr, rk); % 卡尔曼滤波器初始化
kf.Pmin = [avperrset(0.01,1e-4,0.1); gabias(1e-3, [1,10])].^2; % 方差阵最小值
kf.pconstrain=1; % 方差阵上下限约束条件,1:表示约束
len = length(imu); [avp, xkpk] = prealloc(fix(len/nn), 10, 2*kf.n+1); % 对变量预先分配内存
timebar(nn, len, '15-state SINS/GPS Simulation.'); % 程序运行的进度条
ki = 1; % 量测更新的计数器
for k=1:nn:len-nn+1
k1 = k+nn-1;
wvm = imu(k:k1,1:6); t = imu(k1,end); % 角度增量和速度增量,采样时刻
ins = insupdate(ins, wvm); % 惯导更新
kf.Phikk_1 = kffk(ins); % 计算状态转移矩阵
kf = kfupdate(kf); % 卡尔曼滤波器预测更新
if mod(t,1)==0 % 判断是否有GNSS位置量测,此处认为GNSS为整秒量测,mod为求余数函数
posGPS = trj.avp(k1,7:9)' + davp0(7:9).*randn(3,1); % GPS pos simulation with some white noise 模拟GNSS位置量测值
kf = kfupdate(kf, ins.pos-posGPS, 'M'); % 卡尔曼滤波状态反馈
[kf, ins] = kffeedback(kf, ins, 1, 'avp'); % 卡尔曼滤波状态反馈
avp(ki,:) = [ins.avp', t]; % 姿态、速度、位置和时间
xkpk(ki,:) = [kf.xk; diag(kf.Pxk); t]'; ki = ki+1; % 反馈后的剩余状态、方差阵和时间
end
timebar; %
end
avp(ki:end,:) = []; xkpk(ki:end,:) = []; % 释放空间
% show results
insplot(avp); % 调用 insplot 画姿态、速度和位置
avperr = avpcmpplot(trj.avp, avp); % 调用 avpcmpplot 画组合导航计算的avp与参考avp的差值
kfplot(xkpk, avperr, imuerr); % 调用 kfplot 画avp误差、imu误差、反馈后的剩余状态和方差阵
组合导航avp仿真图:与真实轨迹很接近了,最后的轨迹指北
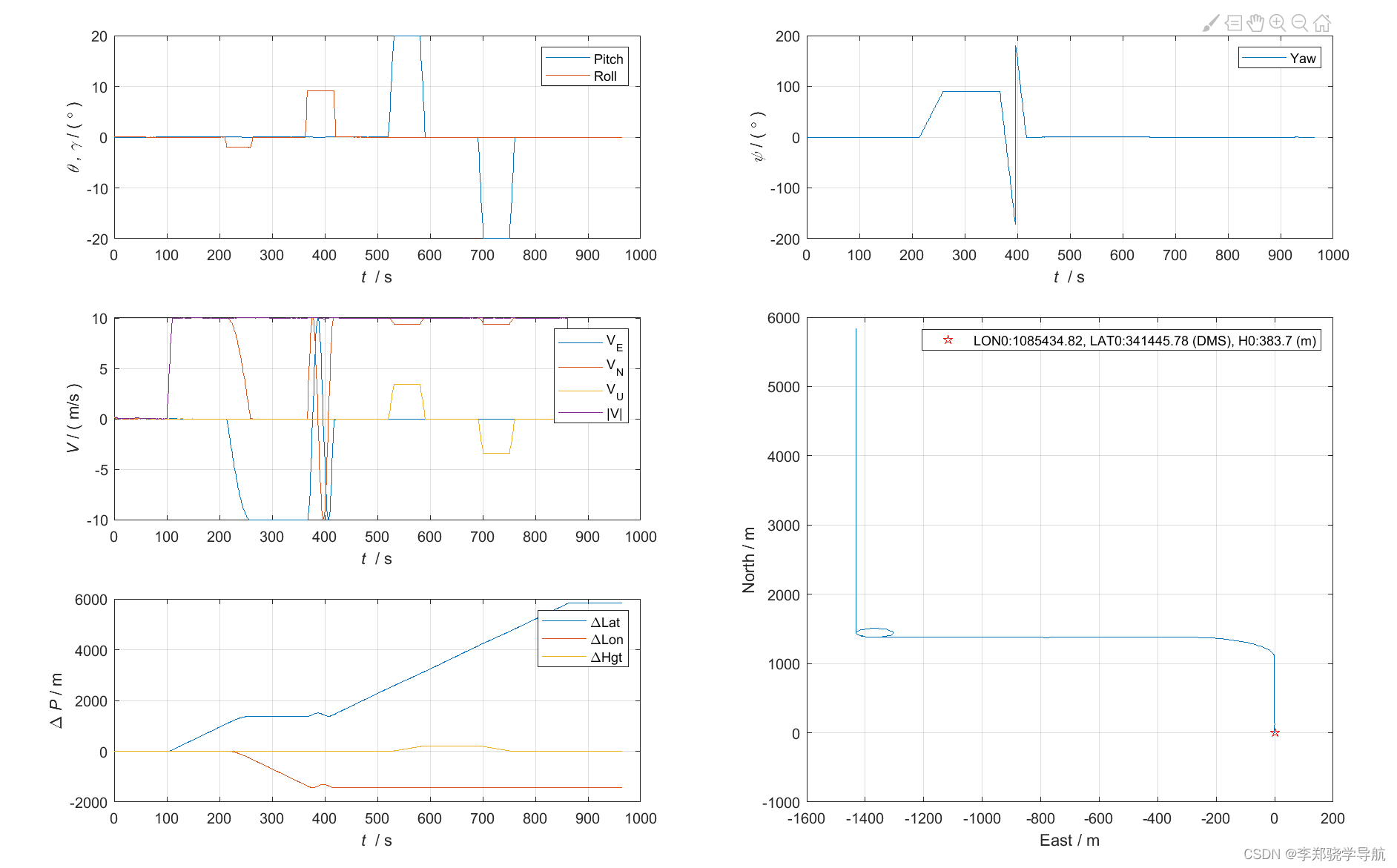
与真实轨迹相比误差图:误差都逐渐收敛
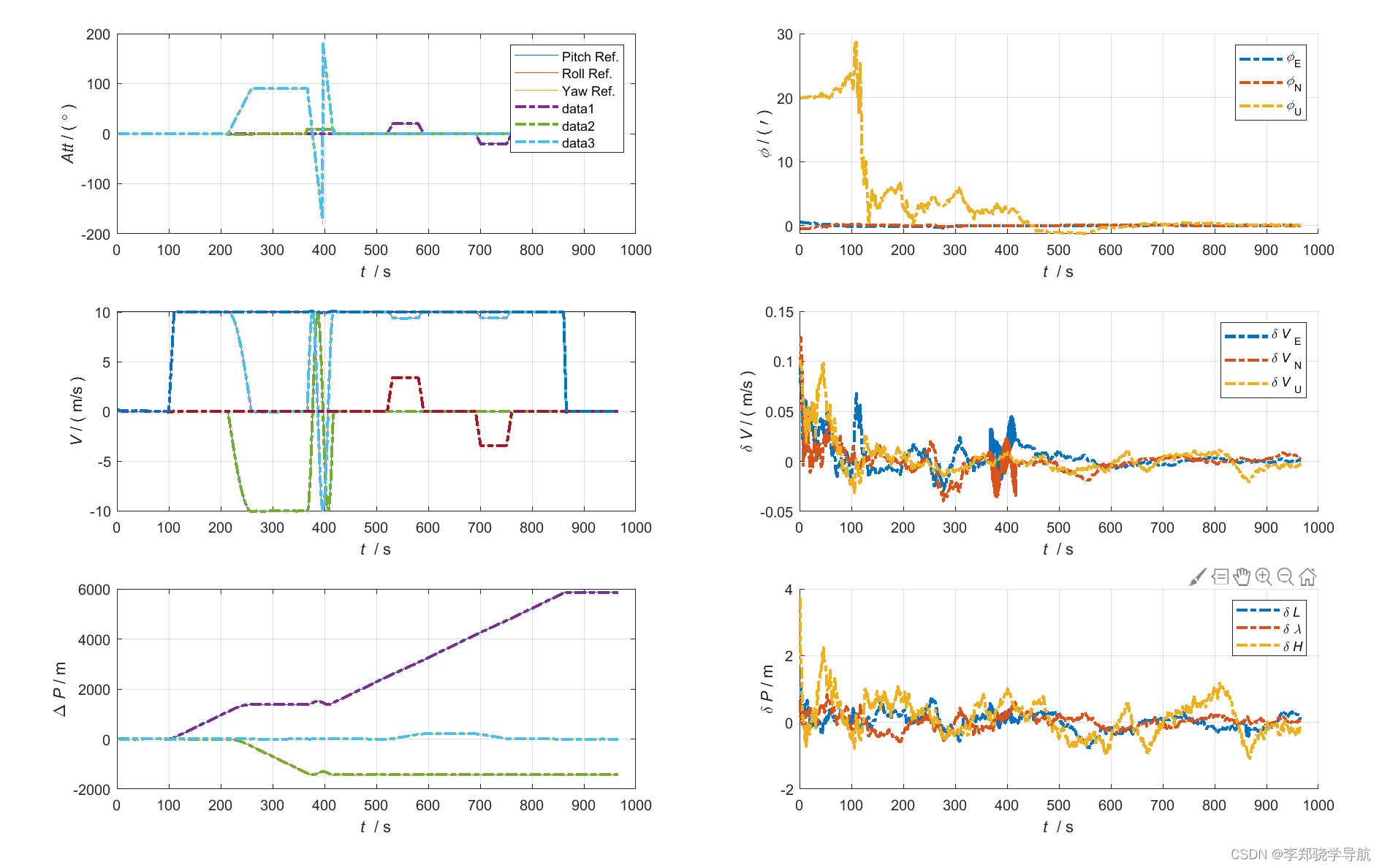
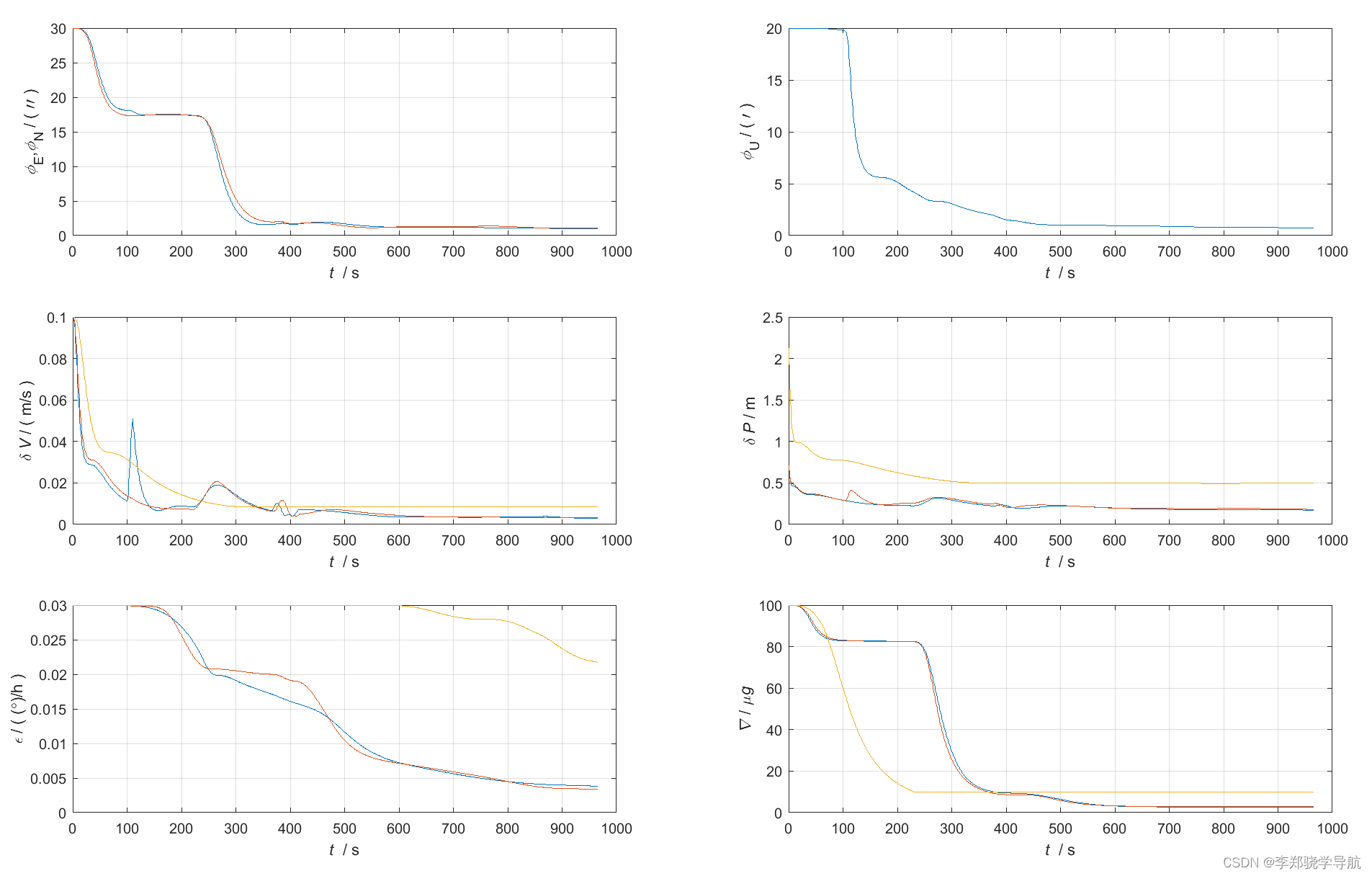
Kalman滤波图:有反馈的会逐渐趋于0,无反馈的趋于常值(与设置的基本吻合),明显能看出天向陀螺仪漂移估计的不如水平陀螺仪漂移
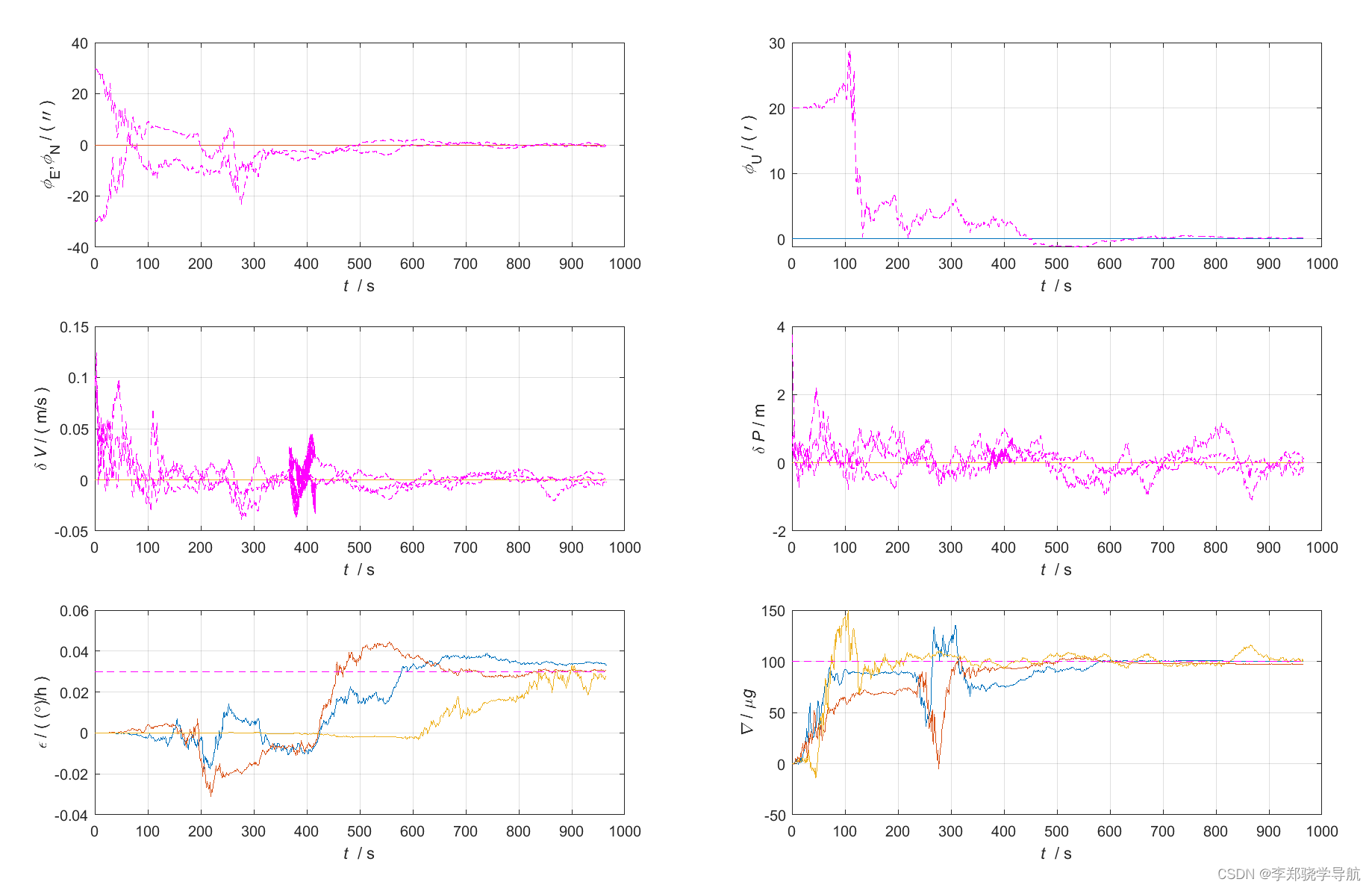
误差图: