二叉树

概念：二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树
特点：每个节点支持两个分支的树结构，相比于单向链表，多了一个分支

二叉查找树

一棵空树，或者是具有下列性质的二叉树：
（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（3）左、右子树也分别为二叉排序树；
特点：它具有二叉查找树的所有特点，同时增加了一个规则：”它的左右两个子树的高度差的绝对值不超过1“。平衡二叉树会采用左旋、右旋的方式来实现平衡。

平衡二叉树

特点：平衡二叉树：它具有二叉查找树的所有特点，同时增加了一个规则：”它的左右两个子树的高度差的绝对值不超过1“。平衡二叉树会采用左旋、右旋的方式来实现平衡。

红黑树

（1）每个节点或者是黑色，或者是红色。

（2）根节点是黑色。

（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！

（4）如果一个节点是红色的，则它的子节点必须是黑色的。

（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点
特点：一条路径不能比其他任意一条路径的两倍还要长

B树

B树就是一个有序的多路查询树

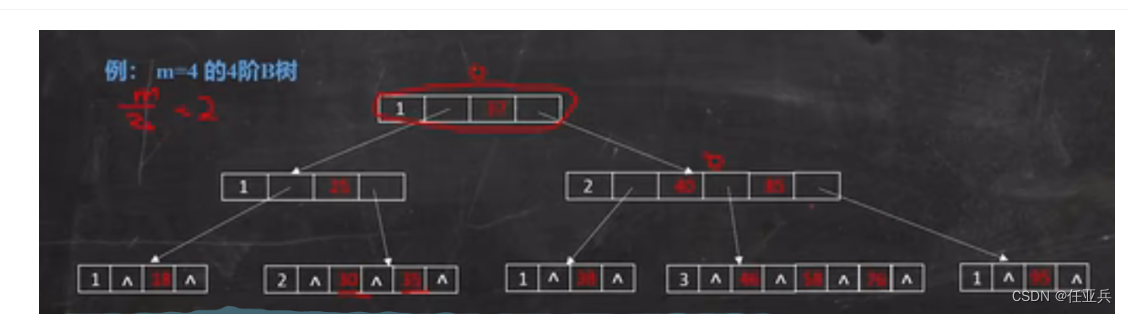
（1） 树中的每个节点最多有个m个孩子节点（最多有m-1)个关键字（元素））
(2) 节点的结构
（3） 除根节点外，其它节点至少有m/2个孩子节点
（4）若根节点不是叶子节点，则根节点至少有两个孩子节点
（5） 所有叶子节点都在同一层上，即B树的所有结点的平衡因子均等于0的多路查找树

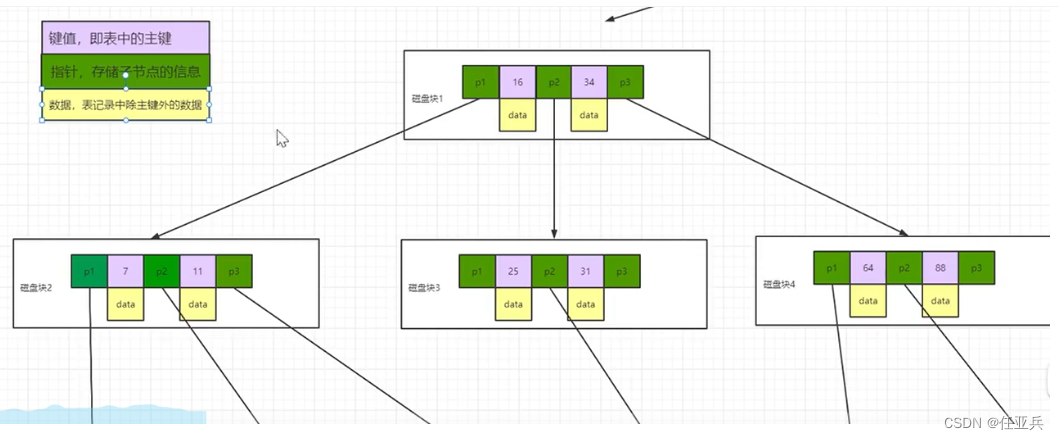
B+树

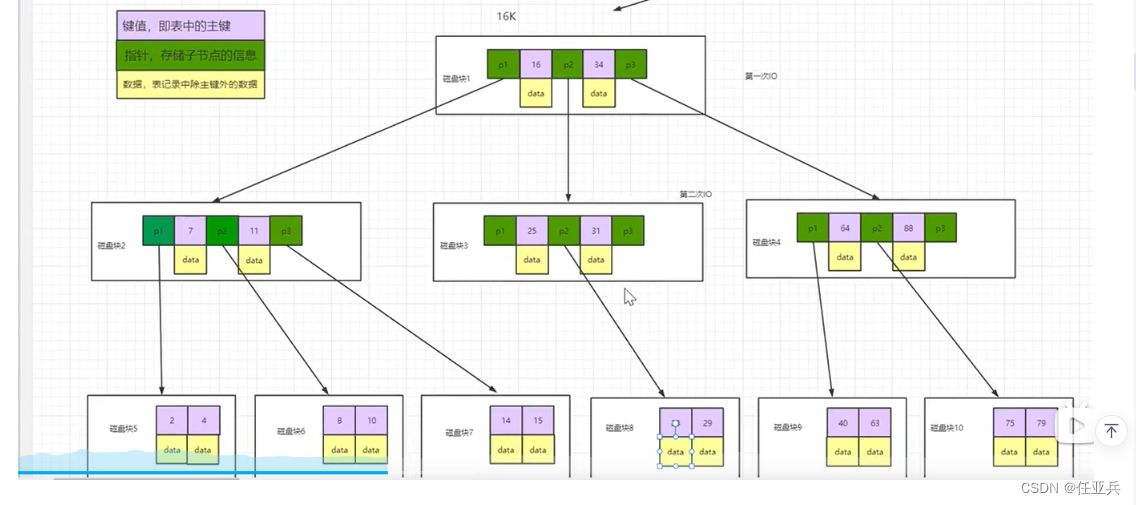
特点：
1.数据只出现在叶子节点（非叶子节点并不存储真正的 data）

2.所有叶子节点增加了一个链指针