LeetCode 392. 判断子序列
链接:392. 判断子序列
双指针:
思路:
本题较容易,如果不用动态规划而是用双指针的办法思路会更加简单。首先两个指针fast,slow分别代表t,s的下标,快指针用于遍历长字符串t,慢指针遍历短字符串s。在遍历字符串之前可以先做一个判断,如果s长于t,则无论如何都无法在t中找到子序列s,直接返回false,如果s长度为0,则直接返回true。
然后是遍历的过程,快指针每次走一步,慢指针在当s[slow]等于t[fast]的时候才走一步,直到慢指针走完,则说明t存在子序列s,否则说明不存在。
代码:
class Solution {
public:
bool isSubsequence(string s, string t) {
if (t.size() < s.size())
return false;
int slow = 0, fast = 0;
if (slow == s.size())
return true;
for (int fast = 0; fast < t.size();fast++)
{
if (t[fast] == s[slow])
slow++;
if (slow == s.size())
return true;
}
return false;
}
};动态规划:
思路:
相比于双指针,动态规划的思路要稍复杂些,但是仔细观察可以发现,本题和1143. 最长公共子序列思路十分相似,如果s和t的最长公共子串为s,则说明s一定是t的子串,照着这个思路,我们可以把最长公共子序列的代码直接照搬过来,最后加一个判断,如果dp[s.size()][t.size()] != s.size(),则说明s和t的最长公共子串不是s,s不为t的子序列,反之亦然。
另外在递推公式有一点需要注意,虽然不影响结果,但其实当s[i-1]不等于t[j-1]的时候,dp[i][j]不应该由dp[i-1][j]和dp[i][j-1]的最大值来决定,实际上dp[i][j]只可能来自dp[i][j-1],原因是当字符不匹配的时候我们不能跳过s的字符,而只能跳过t的字符,因为我们需要找到全部能匹配s的字符的t的子串,一旦跳过了会影响到dp的数值,但好在不影响本题的结果,只要我们最后做了dp数值是否等于s的长度的判断就不会出错。
代码:
class Solution {
public:
bool isSubsequence(string s, string t) {
// dp[i][j]表示长度为[0, i]的s和[0, j]的t的最长公共子序列长度
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1));
for (int i = 1; i <= s.size(); i++)
for (int j = 1; j <= t.size(); j++)
{
if (s[i-1] == t[j-1])
dp[i][j] = dp[i-1][j-1] + 1;
else
dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
if (dp[s.size()][t.size()] != s.size())
return false;
else
return true;
}
};LeetCode 115. 不同的子序列
链接:115. 不同的子序列
思路:
这道题目难度一下子就上来了,我们还是按照动态规划的思路来解。首先定义下标:dp[i][j]表示字符串s中长度为i的子序列出现字符串t中长度为j的子序列的次数。根据定义,我们可以知道,当j为0时,不论s的长度为多少,出现长度为0的子序列的次数都为1,因为此时唯一的方法就是删除s中所有的字符,当然也包括s长度为0的情况,这时就不用删除。所以初始dp数组为dp[i][0] = 1,i的范围取[0, s.size()]。dp数组其余数均初始化为0。
接下来关键的地方是递推公式,当匹配字符的时候,有s[i-1]等于t[j-1]和不等于t[j-1]两种情况,先考虑简单一点的情况。
- s[i-1] != t[j-1]。这种时候的递推公式其实和上一题是一样的,当不相等的时候,跳过当前不匹配的s的字符串 ,令dp[i][j]等于去掉当前字符的上一个s的子字符串的长度i-1,也就是dp[i][j] = dp[i-1][j]。同样我们不能取dp[i][j-1],理由在上一题已经说过了,匹配的字符串t必须是完整的不能跳过。
- s[i-1] == t[j-1]。这种情况就相对复杂一些,首先当当前字符相等的时候,我们肯定可以匹配到当前字符,所以用s[i-1]去匹配t[j-1]时的方法数量为dp[i-1][j-1],但同时我们也可以不选取当前字符去匹配,而尝试用s[i]去匹配t[j-1],考虑这样一个例子:s = "abb", t = "ab",当我们匹配到第二个字符,也就是i和j等于2的时候,我们可以用s[1],也就是s的第一个"b",去匹配t[1],也可以用s[2],也就是s的第二个“b",去匹配t[1],这样一来就有两种结果数量了,前者的结果数量为dp[i-1][j],后者的结果数量为dp[i-1][j-1],那么最终递推公式为dp[i][j] = dp[i-1][j-1] + dp[i-1][j]。
为了方便理解,这里再贴一张dp数组的推导过程,图来自代码随想录
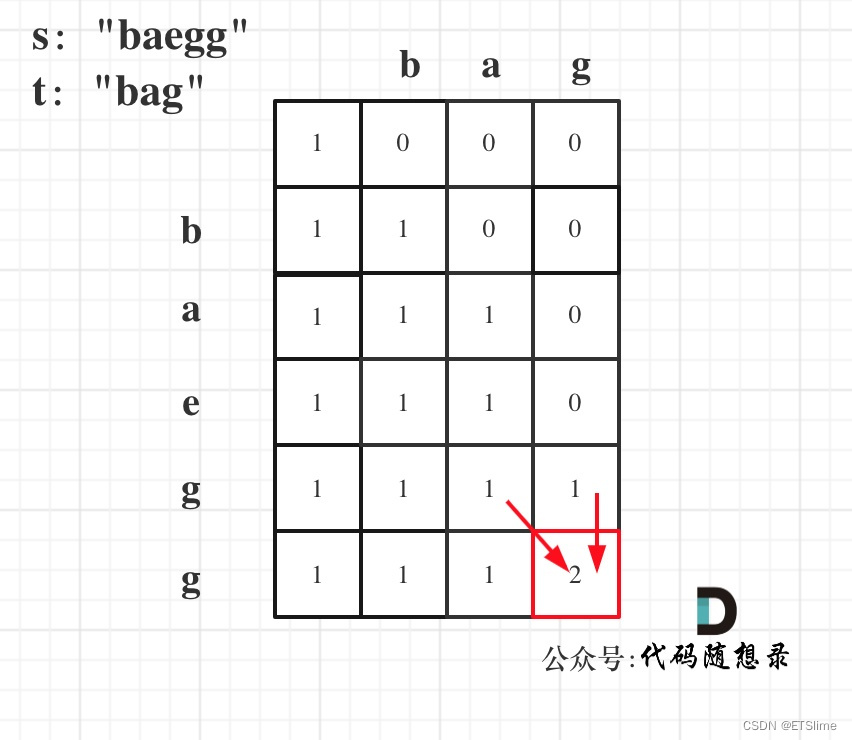
最后,选取最靠右下角的数 dp[s.size()][t.size()]返回即可。
代码:
class Solution {
public:
int numDistinct(string s, string t) {
// dp[i][j]表示以i-1下标结尾的s的子序列出现以j-1下标结尾的t的子字符串的次数
vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));
// 初始化,当j为0时dp[i][0]为1
for (int i = 0; i <= s.size(); i++)
dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++)
for (int i = 1; i <= s.size(); i++)
{
if (s[i-1] != t[j-1])
// 需要用t去匹配,所以j不能动
dp[i][j] = dp[i-1][j];
else
{
// 既可以用s[i-1]去匹配,也可以用s[i]去匹配
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
}
}
return dp[s.size()][t.size()];
}
};