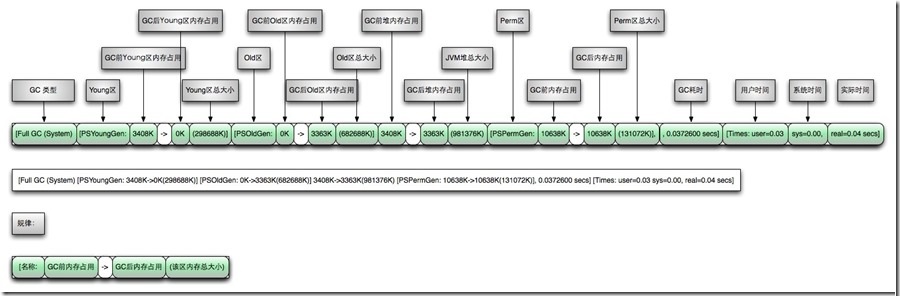
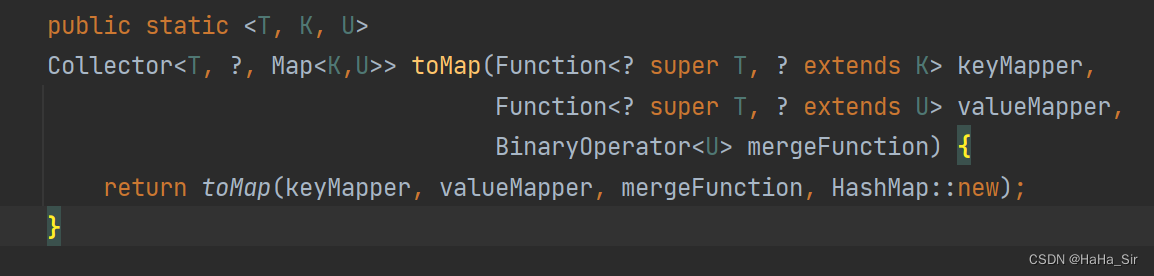
一、LPA-star算法(Lifelong Planning)简介
LPA * ( Lifelong Planning 终身规划 A * )是一种基于A * 的增量启发式搜索算法,被用来处理动态环境下从给定起始点到给定目标点的最短路径问题,即起始点和目标点是固定的。

(注:启发式搜索是利用启发函数来对搜索进行指导,从而实现高效的“智能”搜索,例如A_star算法、遗传算法等。增量搜索是对以前的搜索结果信息进行再利用来实现高效搜索,大大减少搜索范围和时间,例如LPA * 、D * 、D* Lite算法等。)
二、节点的代价与状态
与D * 用 h(X)和 k(X)描述节点代价类似,为了应对动态环境,LPA * 用g(s)和rhs(s)两个值描述节点的代价。g(s)是目前所有次计算中,从起始点到当前节点的最小代价值(符号命名与A * 算法的g(n)类似,与D * 算法中的 k(X)发挥的作用类似) ; rhs(s)是本次计算中,从起始点到当前节点的代价值(与D * 算法中的 h(X)发挥的作用类似)。
根据 g(s) 和 rhs(s) 的大小,定义节点状态。
1)若g(s)=rhs(s),局部一致( Locally Consistent )状态,类似D*算法的Lower态;
2)若g(s)>rhs(s),局部过一致( Locally Overconsistent )状态,表明现在节点s有更理想的父节点使自己到起点的代价值更小,那么此时将设置g(s)=rhs(s),节点便恢复为局部一致状态﹔
3)若g(s)<rhs(s),局部欠一致(Locally Underconsistent)状态, 这种情况通常出现在父辈的某一节点突然变为障碍的情况下,造成父辈节点到起点的路径变大,从而需要修改g(s)的值,如果节点处于这种状态,则当它由优先队列中取出时,将其g值设置为无穷大,即将该节点状态变为局部过连续,而局部过连续的点将会被再次添加到优先队列中,这样就可以在它下次被取出时将其作为局部过连续状态处理,如果需要的话,最终达到局部连续状态。
当一个节点n在局部变得不一致时,它将被放在一个优先队列U(类似A * 算法或 D * 算法中的openList )中进行重新评估。U队列按照节点n的k值(先k1后k2)进行排序,k值定义如下:

上式中的k1类似于A * 算法中的f(n),k2类似于A * 算法中的个g(n),即在选取拓展点时,优先拓展k1值最小的点,当存在多个k1相等的最小点时,再从中选取k2值最小的点进行拓展
三、关键函数及概念
(1)S:地形图中节点的集合,s属于S
(2)c(s,s`):两节点之间的代价函数。
(3)succ(s):successors,节点s的后续节点(子代节点)集合。
(4)pred(s):predecessors,节点s的前代节点(父代节点),与上述succ(s)的意义刚好相反。
(5)g*(s):节点s到起始点的实际最短距离。(这个概念用于对算法进行分析解释,并不参与算法的运算,在算法运行过程中实际发挥作用的是 g(s)和 rhs(s))
(6)g(s):节点s到起始点的预计最短距离,上面那个值是实际的最短距离,这个值是一个预计值,是随着算法求解进程不断变动的,当所有节点的g(s)=rhs(s)时,g(s)的值就是到起始点的实际最短距离,即g(s)=g*(s)。也就是储存节点s曾经的最小值与当前最小值中最小的那个值
(7)rhs(s) :right hand sides,对于s的所有邻接节点,求它们到s的距离加上邻接节点自身的g值,其中最小的那个值作为s的 rhs 值。也就是储存节点s当前的最小代价值
(8)U:LPA * 的优先队列,类似于A * 中的openlist ,依据每个节点的k1和k2值进行排序,拓展时优先选择最小k值进行拓展。
(9)topKey(),返回U队列中k值(按照先k1后k2进行排序)最小的节点;
(10) pop(),从U队列中删除k值最小的节点;
(11)insert(s,k),将具有给定优先级( k值)的节点插入队列;
(12) remove(s),从队列中移除一个节点;
(13)contains(s)如果队列包含指定节点,则返回true,如果不包含指定节点,则返回false ;
四、LPA * 算法总体流程
0、初始化:令优先队列U为空集,将所有节点s存入集合S中,并令每个节点s的g=rhs=inf ;令起始点的rhs值为0,此时起始点的rhs值与g值不相等,即起始点处于局部不一致状态,所以将起始点插入到U中,完成初始化。
1、开始进行循环规划,直至U中的最小k值大于目标点k值时,或者目标点的rhs值与g值相等且不为Inf时,退出循环,完成当前的规划。
2、在每轮循环中,首先获得U队列中的最小k值对应的节点u,并将该节点u从U队列中删除。如果g(u)>rhs(u),即节点u处于局部过一致状态,表明u可以令某个邻近节点作为父节点以获得更优的路径,故令g(u)=rhs(u)。遍历节点u的八邻域子节点(后续节点succ),如果g(u)<=rhs(u),即节点u处于局部欠一致状态或局部一致状态,则将g(u)=inf,使u处于局部过一致状态,遍历u的八邻域子节点和u节点本身(后续节点succ)。
3、对于u的每一个八邻域子节点s(i),遍历节点s(i)的每一个八邻域前向节点p(i)(pred),通过rhs(si)=g(pi)+c(pi,si)计算假设分别将这些节点p(i)作为节点s(i)的父节点时,s(i)的rhs值,并选取他们中最小的rhs值,作为节点s(i)的rhs值,并将对应的pi作为其真正的父节点,此时若节点s(i)处于U中,则将s(i)从U中移除,并判断s(i)的g值与rhs值是否相同,若不相同说明节点s(i)处于局部不一致状态,重新将s(i)节点加入到U中,
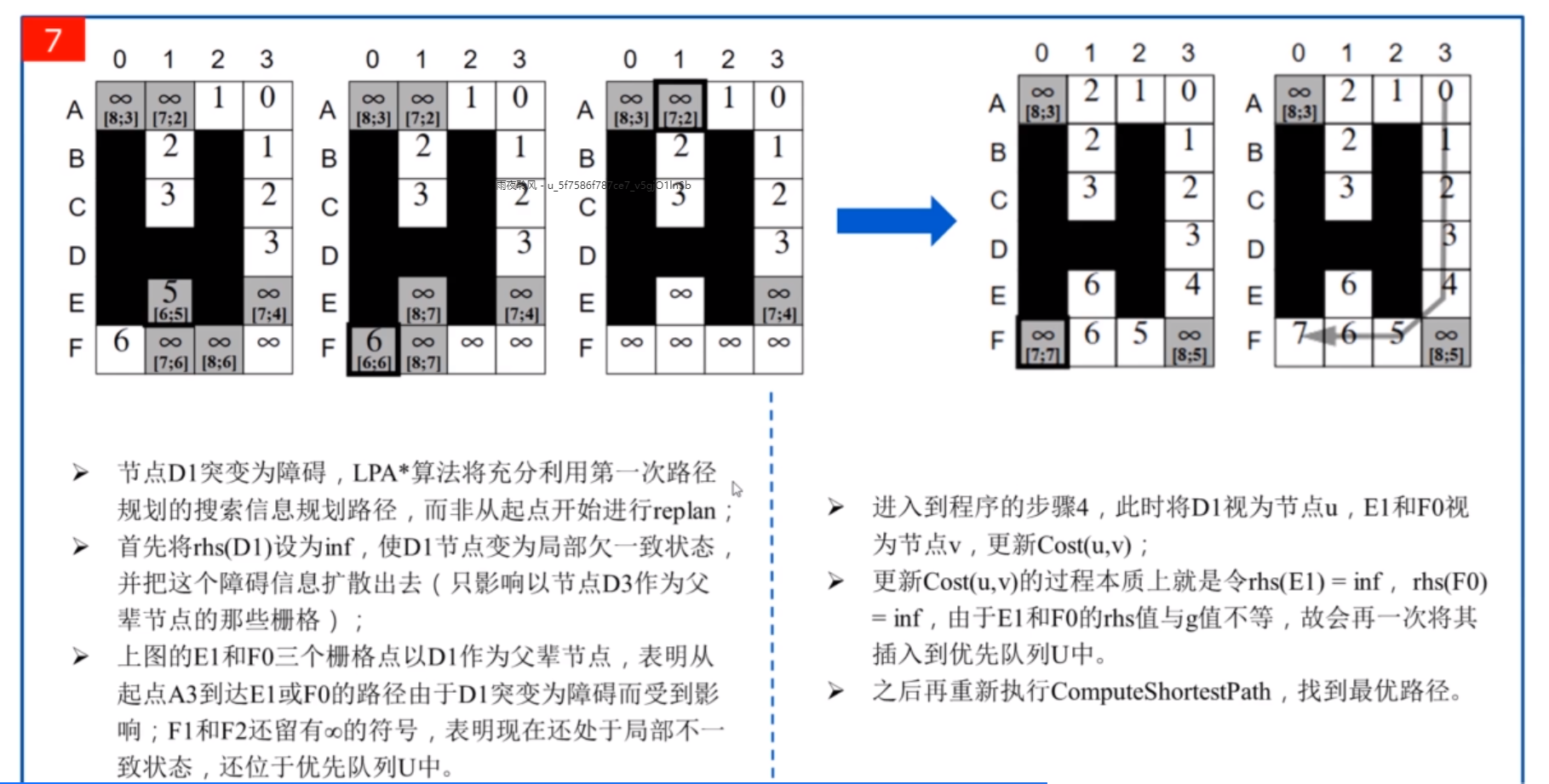
4、 待节点u的每一个八邻域节点s(i)完成以上操作后,本轮循环结束,从队列U中继续挑选k值最小的节点作为新的父节点进行下一轮循环,直至满足退出循环的条件,此时,静态路径规划已经完成,从目标点反推每一个节点的父节点,直到起点,就可以获得从起点至目标点的路径。直到地图突然有障碍物栅格u出现,导致节点间的连接代价发生变化,开始进行动态规划。
5、首先找到所有以障碍物栅格u作为父节点的子代节点v,然后更新u和v节点的代价,实际上就是令受障碍物栅格点u影响的点的rhs值变为inf,使其与g值不等,重新处于局部不一致状态,加入U中进行更新。最后重新执行以上步骤1~3,找到新的最优路径

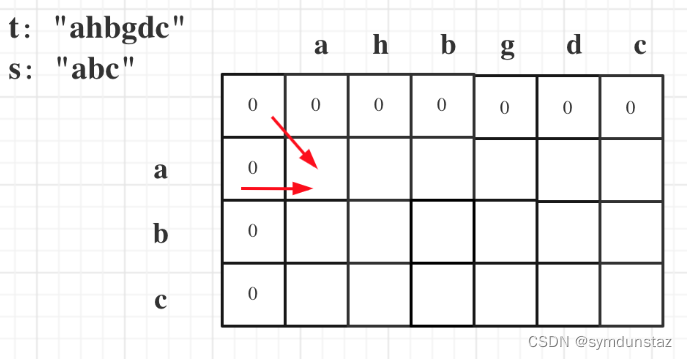
五、LPA * 算法流程示例


六、关键细节深入梳理
1、关于succ与pred的概念问题:个人认为不必过于纠结这两个概念,在ComputeShortestPath函数中进行拓展时,实际上在编程实现时succ完全可以认为是当前拓展点周围八个邻近节点,同样在UpadateVertex函数中,pred完全也可以认为是s’周围的八个邻近节点
2、环境突变后的处理:若环境发生变化,导致之前规划的路径不可行,则开始进入动态规划阶段。
(1)首先,找到所有受影响的节点
对于 每个 突变为障碍物的节点xi,找到其八邻域的相邻节点中 所有 的真正子节点ci(所谓真正的子节点也就是ci中保存的父节点信息为xi),将所有突变为障碍物的节点xi的所有真正子节点ci找到后,再以每个ci为父节点找到他们八邻域相邻节点中所有的真正子节点cci,以此不断的一层层找下去,直至没有子节点。那么所有的受影响的子节点也就找到了,即由ci、cci、ccci . . . . . .等构成的集合
(2)然后,更新突变为障碍物的节点的rhs值和g值
将所有突变为障碍物的节点的rhs值和g值设为inf
(3)更新受影响的节点的rhs值
将ci、cci、ccci . . . . . .等构成的集合中存储的受影响的子节点的rhs值设为inf,并将其添加到U队列中,等待更新,在往U队列中添加时,同时重新计算了这些受影响子节点的k1和k2值,尽管此时k1值和k2值并没有来得急发生改变。
(4)调用ComputeShortestPath函数进行动态规划
主要参考资料:
古月学院 基于栅格地图的机器人路径规划算法指南:【点击此处跳转】