文章目录
- 简介
- CRC思想
- 错误检测
- 基本思想
- 多项式运算
- 没有进位的二进制计算
- CRC计算方式
- 发送方计算
- 接收方校验
- 多项式选择
- CRC实现原理
- CRC8
- 整体处理数据
- 单个处理数据与整体数据处理比较
- 使用查找表加速计算
- 扩展到CRC16
- 整体处理数据
- 单个处理数据与整体数据处理比较
- 使用查找表加速计算
参考http://www.sunshine2k.de/articles/coding/crc/understanding_crc.html#ch44
简介
CRC即循环冗余校验码(Cyclic Redundancy Check):
数据通信领域中最常用的一种查错校验码,其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查(CRC)是一种数据传输检错功能,对数据进行多项式计算,并将得到的结果附在帧的后面,接收设备也执行类似的算法,以保证数据传输的正确性和完整性。
CRC思想
错误检测
错误检测的目的是使消息接收方在接收到消息时, 检测该消息是否在传输过程中被损坏。
Message : 6 23
Message with checksum : 6 23 29
Message after transmission: 6 27 29
上述例子中,使用累加的办法计算出8字节校验和:(6 + 23)mod 256,然后将结果附在消息后边进行传输,接收方就可以进行数据校验。
假设如下消息被接收后,使用此种方式并不能检测出来,此时需要一个更好的错误检测方法
Message after transmission: 8 21 29
基本思想
CRC算法基本思想是将消息视作一个大的二进制数据,然后除以一个固定的二进制数,得到的余数即是校验码,接收方可以执行相同的除法,然后将余数与校验和进行比较。
如消息为(6, 23)两个字节,可以视为16进制的0x0617,二进制0000-0110-0001-0111,然后使用一个固定的二进制除数1001,得出余数为0010,即十进制的1559除以9,得到余数2。
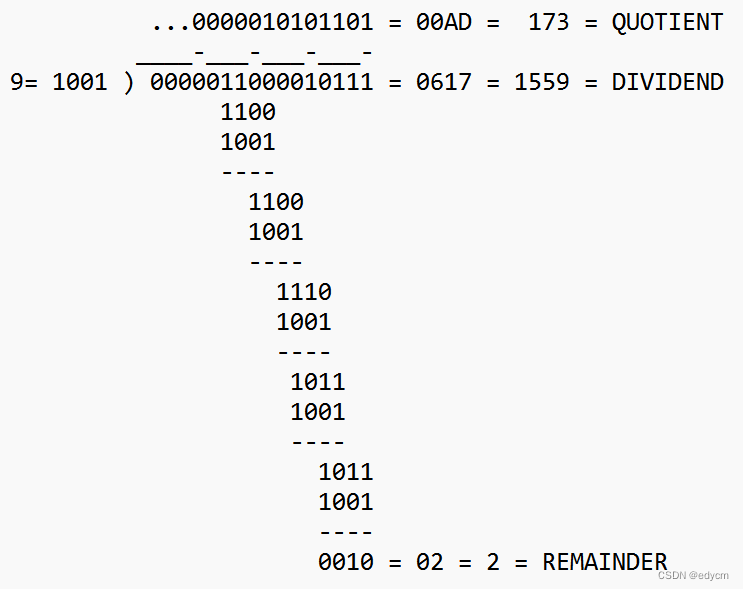
如上例中(6, 23)->(8, 21),使用除法就可以进行校验:
将(8, 21)视为0x0815,即十进制数2069,除以9,得到余数为8,与原来计算的2不一致。
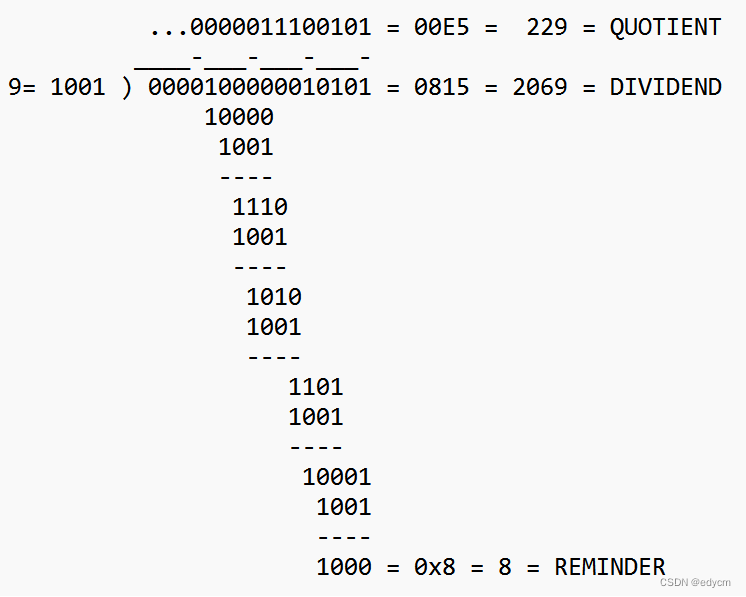
使用除法在计算过程中,余数会产生很多变化,如果更多字节加入到消息中,计算结果会很快发生根本性的变化,这是加法做不到的地方。
多项式运算
可以将一个二进制数据看成一个多项式,如十进制数23,二进制为10111,可以将其看成这样一个多项式:
1x^4 + 0x^3 + 1x^2 + 1x^1 + 1*x^0
简单地就是:
x^4 + x^2 + x^1 + x^0
使用这种方法,比如我们想计算1101乘以1011,就可以使用多项式进行计算:
(x^3 + x^2 + x0)(x3 + x^1 + x^0) = x^6 + x^5 + x^4 + 3*x^3 + x^2 + x^1 + x^0
我们知道x就是2,所以可以进行进位将3*x3看成x4+x^3,这样公式可以简化为:
x^7 + x^3 + x^2 + x^1 + x^0
这里把基数x抽象出来的重点是,如果我们不知道x的具体值,就不能执行进位,可以将x2和x3看成不一样的类型,每个系数当成不同的类型被分离开,这里存在一个特殊的多项式算术,即所有的多项式系数必须为0或1,可以看作为有限域[0, 1],多项式的系数即为MOD 2;因此之前的计算结果为:
(x^3 + x^2 + x0)(x3 + x^1 + x^0) = x^6 + x^5 + x^4 + 3*x^3 + x^2 + x^1 + x^0
= x^6 + x^5 + x^4 + x^3 + x^2 + x^1 + x^0
这种计算方法也可以看作没有进位的二进制计算
没有进位的二进制计算
在CRC的计算过程中都是以没有进位的二进制进行计算的,例如:
加法:0+0=0 0+1=1 1+0=1 1+1=0
减法:0-0=0 1-0=1 1-1=0 0-1=1
这种计算方式会使一些概念变得没有意义,如1010并不比1001大,因为1001可以通过1010加减同一个数得到:
1001 = 1010 + 0011
1001 = 1010 - 0011
乘法:1101 * 1011 = 1101 + 11010 + 0000 + 1101000 = 1111111(1101根据1011左移然后求和)
除法:较为复杂一点,就是如何界定x要大于y,定义:当x最高位为1的位置大于或等于Y最高位为1的位置,例如:10110111 除以 10110
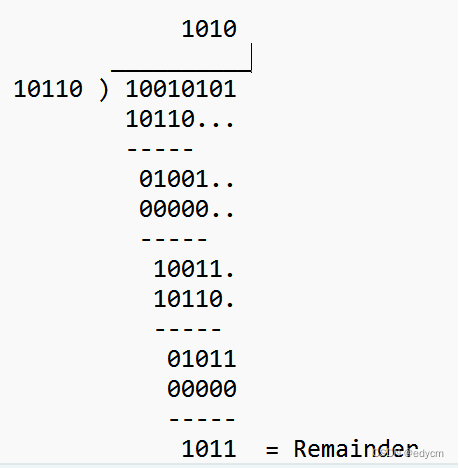
如果一个二进制数B可以通过二进制数A进行移位并与0进行XOR,则表明B可以被A整除如:
0000 ^ 0011 = 0011 ^ 0110 = 0101 ^ 1100 = 1001
CRC计算方式
发送方计算
在计算之前最重要的就是先选择一个多项式(poly)的除数,这个多项式可以任意选择,但是有一些多项式经过验证是比其他多项式好的;
多项式的宽度(MSB)在整个计算中是很重要的;如现在我们选择多项式为10011,它的宽度是4,而不是5;
选定多项式后,就可以进行计算,如:
原始消息(m(x)):1101011011
多项式(g(x)):10011
附加多项式的宽度个0后的消息(用于填充校验码):11010110110000

然后我们将计算结果附加到消息后边
发送的消息为 (t(x)):11010110111110
接收方校验
接收者可以通过两种方式来验证消息是否完整:
分离消息和校验和,计算附加多项式的宽度个0后的消息的校验和与消息中的校验和进行比较
通过接收到的消息和多项式直接计算校验和,验证是否为0
原理:t(x) = m(x) - m(x) mod g(x),得出t(x) mod g(x) = 0

多项式选择
传输的消息:T(x),多项式:G(x),产生的损坏:E(x)
(T(x) + E(x)) mod G(x) ?= 0
根据之前的说明:
T(x) mod G(x) = 0
所以对于所有情况,需要找出一个G(x),使得E(x) mod G(x) != 0,之前讲过可以将二进制转换成多项式:
- 单bit错误,即E(x) = xi,最简单的就是使用至少两位的G
eg:G(x) = xi + xj 即 E(x) / G(x) = xi / (xi + xj) = 1 / (1 + xj-i),很明显会得到一个小数,即不能整除 - 2个bit错误,即E(x) = xi+xj(x > j) = xj(xj-i + 1) = xj(xk + 1),这个就比较复杂了,可以找出一些例子,比如G(x) = x16 + x12 + x5 + 1 作用于 k <= 32751,可以检测出任意两位的错误
- 更多位错误:参考:https://users.ece.cmu.edu/~koopman/crc/
汉明距离:二进制A最少变换多少位可以转化位B,变换的位数就是汉明距离,此处可理解位多少位发生错误
CRC实现原理
整体处理数据:将所有要处理的数据看作一个大的二进制数,并填充多项式宽度位的0
单个处理数据:一个字节一个字节进行处理,最终得到与整体数据处理相同的结果;单个数据处理较为特殊,即先填充多项式宽度位0,然后与多项式进行取余。
CRC8
整体处理数据
需处理的数据:0xC2, 多项式0x1D,实际除数为100011101,
计算校验和过程:
11000010 00000000
100011101
---------
010011001
100011101
---------
000101111
100011101
100011101
100011101
---------
001100101
100011101
100011101
---------
010001001
100011101
---------
000001111 = 0x0F
// single byte
public static byte Compute_CRC8_Simple_OneByte_ShiftReg(byte byteVal)
{
const byte generator = 0x1D;
byte crc = 0; /* init crc register with 0 */
/* append 8 zero bits to the input byte */
byte[] inputstream = new byte[] { byteVal, 0x00 };
/* handle each bit of input stream by iterating over each bit of each input byte */
foreach (byte b in inputstream)
{
for (int i = 7; i >= 0; i--)
{
/* check if MSB is set */
if ((crc & 0x80) != 0)
{ /* MSB set, shift it out of the register */
crc = (byte)(crc << 1);
/* shift in next bit of input stream:
* If it's 1, set LSB of crc to 1.
* If it's 0, set LSB of crc to 0. */
crc = ((byte)(b & (1 << i)) != 0) ? (byte)(crc | 0x01) : (byte)(crc & 0xFE);
/* Perform the 'division' by XORing the crc register with the generator polynomial */
crc = (byte)(crc ^ generator);
}
else
{ /* MSB not set, shift it out and shift in next bit of input stream. Same as above, just no division */
crc = (byte)(crc << 1);
crc = ((byte)(b & (1 << i)) != 0) ? (byte)(crc | 0x01) : (byte)(crc & 0xFE);
}
}
}
return crc;
}
优化处理:
对于除数说明:100011101,即可理解为,只有当被除数的第9位为1时才认为被除数比除数大,即需要运算,所以可以先判断最高位是否为1(x & 0x80),如果是则直接左移,并与00011101(多项式)进行异或运算
1100001000000000
100011101
---------
10011001
100011101
---------
0010111100
100011101
---------
0011001010
100011101
---------
010001001
100011101
---------
00001111 = 0x0F
// single byte
public static byte Compute_CRC8_Simple_OneByte(byte byteVal)
{
const byte generator = 0x1D;
byte crc = byteVal; /* init crc directly with input byte instead of 0, avoid useless 8 bitshifts until input byte is in crc register */
for (int i = 0; i < 8; i++)
{
if ((crc & 0x80) != 0)
{ /* most significant bit set, shift crc register and perform XOR operation, taking not-saved 9th set bit into account */
crc = (byte)((crc << 1) ^ generator);
}
else
{ /* most significant bit not set, go to next bit */
crc <<= 1;
}
}
return crc;
}
单个处理数据与整体数据处理比较
单个个字节处理
00000001 00000000
1 00011101
-------------
0 00011101 = Remainder
比较:
对比:
单字节处理完第一个字节结果(A):00011101
第二个字节数据(B) :00000010
整体数据处理完第一个字节结果©:00011111
结论:C = A XOR B
得出一个个字节计算出校验和的方式:
// byte array
public static byte Compute_CRC8_Simple(byte[] bytes)
{
const byte generator = 0x1D;
byte crc = 0; /* start with 0 so first byte can be 'xored' in */
foreach (byte currByte in bytes)
{
crc ^= currByte; /* XOR-in the next input byte */
for (int i = 0; i < 8; i++)
{
if ((crc & 0x80) != 0)
{
crc = (byte)((crc << 1) ^ generator);
}
else
{
crc <<= 1;
}
}
}
return crc;
}
使用查找表加速计算
回顾一下之前字节数组处理流程(data{0x01,0x02}, poly: 0x1D):
- 初始化crc为0x00
- crc XOR 输入字节0x01:0x00 ^ 0x01 = 0x01
- crc mod poly:0x01 mod ox1D = 0x1D
- 重复2、3步,知道计算完所有字节
这其中可以发现,使用crc对poly取余这一步可以优化,即可以先记录一个查找表,记录所有[0x00, 0xFF]对poly取余的结果,省略这一步的计算
// generate crc_8 lookup table
public static void CalulateTable_CRC8()
{
const byte generator = 0x1D;
crctable = new byte[256];
/* iterate over all byte values 0 - 255 */
for (int divident = 0; divident < 256; divident++)
{
byte currByte = (byte)divident;
/* calculate the CRC-8 value for current byte */
for (byte bit = 0; bit < 8; bit++)
{
if ((currByte & 0x80) != 0)
{
currByte <<= 1;
currByte ^= generator;
}
else
{
currByte <<= 1;
}
}
/* store CRC value in lookup table */
crctable[divident] = currByte;
}
}
// calc crc_8
public static byte Compute_CRC8(byte[] bytes)
{
byte crc = 0;
foreach (byte b in bytes)
{
/* XOR-in next input byte */
byte data = (byte)(b ^ crc);
/* get current CRC value = remainder */
crc = (byte)(crctable[data]);
}
return crc;
}
扩展到CRC16
整体处理数据
输入数据{0x01, 0x02},多项式:0x1021
整体数据处理(判断最高位0x80 -> 0x8000):
00000001 00000010 00000000 00000000
1 00010000 00100001
-------------------
0 00010010 00100001 = 0x1221 处理完第一个字节结果
10001 00000010 0001
-------------------
00011 00100011 0001
10 00100000 0100001
-------------------
01 00000011 0101001
1 00010000 00100001
-----------------------
0 000100110 1110011 = 0x1373
单个处理数据与整体数据处理比较
单个个字节处理
单字节字节处理:
00000001 00000000 00000000 00000000
1 00010000 00100001
-----------------------------
0 00010000 00100001
比较:
对比:
单字节处理完第一个字节结果(A) :00010000 00100001
第二个字节数据(B) :00000000 00000010
整体数据处理完第一个字节结果© :00010010 00100001
结论:C = A XOR (B << 8)
得出一个个字节计算出校验和的方式:
// calc crc_16
public static ushort Compute_CRC16_Simple(byte[] bytes)
{
const ushort generator = 0x1021; /* divisor is 16bit */
ushort crc = 0; /* CRC value is 16bit */
foreach (byte b in bytes)
{
crc ^= (ushort(b << 8); /* move byte into MSB of 16bit CRC */
for (int i = 0; i < 8; i++)
{
if ((crc & 0x8000) != 0) /* test for MSB = bit 15 */
{
crc = (ushort((crc << 1) ^ generator);
}
else
{
crc <<= 1;
}
}
}
return crc;
}
使用查找表加速计算
回顾一下之前字节数组处理流程(data{0x01,0x02}, poly: 0x1021):
- 初始化crc为0x0000
- crc XOR 输入字节0x01左移8位:0x0000 ^ (0x01 << 8) = 0x0100
- crc mod poly:0x0100 mod 0x1021 = 0x1221
- 重复2、3步,知道计算完所有字节
与crc8一样,可以记录一个查找表,记录所有[0x00, 0xFF]对poly取余的结果;唯一的区别是,取余时使用的是crc的高8位数据,即crc右移8位数据进行查表。
以及crc迭代结果时是crc >> 8 ^ table[pos];右移8是因为我们是处理的8个字节,而高8位数据以及通过查表的方式对多项式取余了,所以只剩下后边的数据需要进行处理。
// generate crc_16 lookup table
public static void CalculateTable_CRC16()
{
const ushort generator = 0x1021;
crctable16 = new ushort[256];
for (int divident = 0; divident < 256; divident++) /* iterate over all possible input byte values 0 - 255 */
{
ushort curByte = (ushort(divident << 8); /* move divident byte into MSB of 16Bit CRC */
for (byte bit = 0; bit < 8; bit++)
{
if ((curByte & 0x8000) != 0)
{
curByte <<= 1;
curByte ^= generator;
}
else
{
curByte <<= 1;
}
}
crctable16[divident] = curByte;
}
}
// calc crc_16
public static ushort Compute_CRC16(byte[] bytes)
{
ushort crc = 0;
foreach (byte b in bytes)
{
/* XOR-in next input byte into MSB of crc, that's our new intermediate divident */
byte pos = (byte)( (crc >> 8) ^ b); /* equal: ((crc ^ (b << 8)) >> 8) */
/* Shift out the MSB used for division per lookuptable and XOR with the remainder */
crc = (ushort)((crc << 8) ^ (ushort)(crctable16[pos]));
}
return crc;
}