本节目标理解梯度下降的原理,主要围绕以下几个问题展开:
- 梯度下降法的用途?
- 什么是梯度?
- 为什么是负的梯度
- 为什么局部下降最快的方向就是梯度的负方向。
需要的知识储备:一级泰勒展开公式
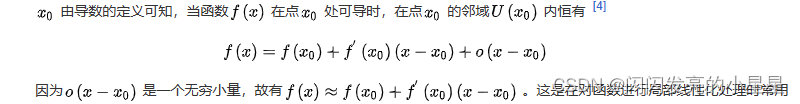
向量内积计算公式
1. 梯度下降算法
无论是在线性回归(Linear Regression)、逻辑回归(Logistic Regression)还是神经网络(Neural Network)等等,都会用到梯度下降算法。梯度下降算法主要用于辅助更新模型参数,使得损失函数最小化。
损失函数为凸函数,目标找到能使函数值最小的参数。我们将该过程类比做下山。 走一步算一步,也就是每次沿着当前位置最陡峭最易下山的方向前进一小步,然后继续沿下一个位置最陡方向前进一小步。这样一步一步走下去,一直走到觉得我们已经到了山脚。这里的下山最陡的方向就是梯度的负方向。
梯度下降算法的公式为:

其中,η为学习因子,即下山每次前进的一小步的长度;θ0 为自变量,即下山位置的坐标,θ为更新后的位置。
沿着负梯度方向更新是结论,那么,为什么是梯度,为什么是负方向呢。
2. 什么是梯度
通俗来说,梯度就是表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在当前位置的导数。
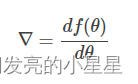
上式中,θ是自变量,f是关于θ的函数。
3. 为什么是负梯度方向 (类比角度,理解为什么是负)
从直观角度理解想象下:
假设中间是山谷,两边都是山。 当在左边的山上要下坡时,梯度为负,x需要往山谷靠近,即x要有右移,增大,则应该是+负梯度;同理分析当在山谷右边要移动到山谷时的情景。
4. 为什么是负梯度方向(数学角度)
一级泰勒展开式
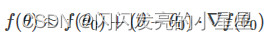
梯度下降数学原理
先写出一阶泰勒展开式的表达式:

其中,是η矢量,它的大小就是我们之前讲的步进长度,类比于下山过程中每次前进的一小步,v为标量,而的单位向量用表示。则可表示为:

特别需要注意的是,不能太大,因为太大的话,线性近似就不够准确,一阶泰勒近似也不成立了。替换之后,的表达式为:
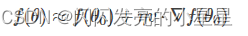
重点来了,局部下降的目的是希望每次更新,都能让函数值变小。也就是说,上式中,我们希望。则有:

因为为标量,且一般设定为正值,所以可以忽略,不等式变成了: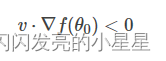
上面这个不等式非常重要!v和Δf都是向量,是当前位置的梯度方向,表示下一步前进的单位向量,是需要我们求解的,有了它,就能根据确定值了。
想要两个向量的乘积小于零,根据向量积公式:
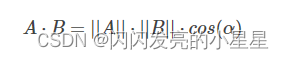
则,当与互为反向,即为当前梯度方向的负方向的时候,能让最大程度地小,也就保证了的方向是局部下降最快的方向。
知道是的反方向后,可直接得到:

之所以要除以的模,是因为是单位向量。
求出最优解之后,带入到中,得: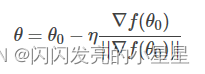
一般地,因为是标量,可以并入到步进因子中,即简化为:

这样,我们就推导得到了梯度下降算法中的更新表达式。