视觉SLAM十四讲——ch10的实践操作及避坑
- 0. 实践前小知识介绍
- 1. 实践操作前的准备工作
- 2. 实践过程
- 2.1 g2o原生位姿图
- 2.2 李代数上的位姿图优化
- 3. 遇到的问题及解决办法
- 3.1 在运行pose_graph_g2o_lie时出现错误
0. 实践前小知识介绍
视觉SLAM(Simultaneous Localization and Mapping)后端是一种用于处理视觉SLAM问题的算法。视觉SLAM是指机器在未知环境中同时实现自身的定位和地图构建的技术。
视觉SLAM后端的任务是在视觉SLAM中负责维护一个优化后的地图和机器人的轨迹。常见的视觉SLAM后端算法包括基于图优化的方法,如G2O、ceres等,以及基于滤波器的方法,如卡尔曼滤波器、扩展卡尔曼滤波器等。
视觉SLAM后端算法需要处理传感器数据的噪声和不确定性,并通过优化算法来减小误差和提高精度。同时,视觉SLAM后端算法还需要快速、高效地处理大量的数据,并对计算结果进行实时更新和优化。
视觉SLAM后端算法在自主驾驶、无人机、机器人等领域有广泛的应用。
1. 实践操作前的准备工作
- 在终端中进入ch10文件夹下,顺序执行以下命令进行编译。
mkdir build
cd build
cmake ..
//注意,j8还是其他主要看自己的电脑情况
make -j8
- 在build文件中进行运行。
注意: 在make过程中,会出现warning,但是对我们此实践的过程几乎没有影响。
2. 实践过程
2.1 g2o原生位姿图
在build中执行语句:
./pose_graph_g2o_SE3 /home/fighter/slam/slambook2/ch10/sphere.g2o
运行结果:
生成文件result.g2o;终端输出:
read total 2500 vertices, 9799 edges.
optimizing ...
iteration= 0 chi2= 1023011093.967641 time= 0.616354 cumTime= 0.616354 edges= 9799 schur= 0 lambda= 805.622433 levenbergIter= 1
iteration= 1 chi2= 385118688.233187 time= 0.363139 cumTime= 0.979494 edges= 9799 schur= 0 lambda= 537.081622 levenbergIter= 1
iteration= 2 chi2= 166223726.693657 time= 0.350041 cumTime= 1.32953 edges= 9799 schur= 0 lambda= 358.054415 levenbergIter= 1
iteration= 3 chi2= 86610874.269316 time= 0.351792 cumTime= 1.68133 edges= 9799 schur= 0 lambda= 238.702943 levenbergIter= 1
iteration= 4 chi2= 40582782.710190 time= 0.388134 cumTime= 2.06946 edges= 9799 schur= 0 lambda= 159.135295 levenbergIter= 1
iteration= 5 chi2= 15055383.753041 time= 0.377086 cumTime= 2.44655 edges= 9799 schur= 0 lambda= 101.425210 levenbergIter= 1
iteration= 6 chi2= 6715193.487655 time= 0.363641 cumTime= 2.81019 edges= 9799 schur= 0 lambda= 37.664667 levenbergIter= 1
iteration= 7 chi2= 2171949.168382 time= 0.383848 cumTime= 3.19404 edges= 9799 schur= 0 lambda= 12.554889 levenbergIter= 1
iteration= 8 chi2= 740566.827049 time= 0.376922 cumTime= 3.57096 edges= 9799 schur= 0 lambda= 4.184963 levenbergIter= 1
iteration= 9 chi2= 313641.802464 time= 0.367001 cumTime= 3.93796 edges= 9799 schur= 0 lambda= 2.583432 levenbergIter= 1
iteration= 10 chi2= 82659.743578 time= 0.356125 cumTime= 4.29408 edges= 9799 schur= 0 lambda= 0.861144 levenbergIter= 1
iteration= 11 chi2= 58220.369189 time= 0.326571 cumTime= 4.62065 edges= 9799 schur= 0 lambda= 0.287048 levenbergIter= 1
iteration= 12 chi2= 52214.188561 time= 0.34423 cumTime= 4.96488 edges= 9799 schur= 0 lambda= 0.095683 levenbergIter= 1
iteration= 13 chi2= 50948.580336 time= 0.344858 cumTime= 5.30974 edges= 9799 schur= 0 lambda= 0.031894 levenbergIter= 1
iteration= 14 chi2= 50587.776729 time= 0.323255 cumTime= 5.633 edges= 9799 schur= 0 lambda= 0.016436 levenbergIter= 1
iteration= 15 chi2= 50233.038802 time= 0.321105 cumTime= 5.9541 edges= 9799 schur= 0 lambda= 0.010957 levenbergIter= 1
iteration= 16 chi2= 49995.082839 time= 0.321401 cumTime= 6.2755 edges= 9799 schur= 0 lambda= 0.007305 levenbergIter= 1
iteration= 17 chi2= 48876.738967 time= 0.702032 cumTime= 6.97753 edges= 9799 schur= 0 lambda= 0.009298 levenbergIter= 2
iteration= 18 chi2= 48806.625522 time= 0.373531 cumTime= 7.35107 edges= 9799 schur= 0 lambda= 0.006199 levenbergIter= 1
iteration= 19 chi2= 47790.891373 time= 0.764476 cumTime= 8.11554 edges= 9799 schur= 0 lambda= 0.008265 levenbergIter= 2
iteration= 20 chi2= 47713.626582 time= 0.344026 cumTime= 8.45957 edges= 9799 schur= 0 lambda= 0.005510 levenbergIter= 1
iteration= 21 chi2= 46869.323689 time= 0.698816 cumTime= 9.15838 edges= 9799 schur= 0 lambda= 0.007347 levenbergIter= 2
iteration= 22 chi2= 46802.585509 time= 0.359225 cumTime= 9.51761 edges= 9799 schur= 0 lambda= 0.004898 levenbergIter= 1
iteration= 23 chi2= 46128.758041 time= 0.631884 cumTime= 10.1495 edges= 9799 schur= 0 lambda= 0.006489 levenbergIter= 2
iteration= 24 chi2= 46069.133541 time= 0.309911 cumTime= 10.4594 edges= 9799 schur= 0 lambda= 0.004326 levenbergIter= 1
iteration= 25 chi2= 45553.862164 time= 0.622007 cumTime= 11.0814 edges= 9799 schur= 0 lambda= 0.005595 levenbergIter= 2
iteration= 26 chi2= 45511.762616 time= 0.311606 cumTime= 11.393 edges= 9799 schur= 0 lambda= 0.003730 levenbergIter= 1
iteration= 27 chi2= 45122.762999 time= 0.61714 cumTime= 12.0102 edges= 9799 schur= 0 lambda= 0.004690 levenbergIter= 2
iteration= 28 chi2= 45095.174397 time= 0.31117 cumTime= 12.3213 edges= 9799 schur= 0 lambda= 0.003127 levenbergIter= 1
iteration= 29 chi2= 44811.248505 time= 0.608863 cumTime= 12.9302 edges= 9799 schur= 0 lambda= 0.003785 levenbergIter= 2
saving optimization results ...
实践中使用的时列文伯格—马夸尔特下降的方式,迭代次数选择的三十次。
打开文件result.g2o:
在终端运行:
g2o_viewer result.g2o
运行图为(使用g2o自带的顶点与边求解的结果):

2.2 李代数上的位姿图优化
在build中执行语句:
./pose_graph_g2o_lie /home/fighter/slam/slambook2/ch10/sphere.g2o
运行结果:
生成文件result_lie.g2o;终端输出:
read total 2500 vertices, 9799 edges.
optimizing ...
iteration= 0 chi2= 674837160.579968 time= 0.419014 cumTime= 0.419014 edges= 9799 schur= 0 lambda= 6658.554263 levenbergIter= 1
iteration= 1 chi2= 234706314.970484 time= 0.307203 cumTime= 0.726217 edges= 9799 schur= 0 lambda= 2219.518088 levenbergIter= 1
iteration= 2 chi2= 142146174.348537 time= 0.306181 cumTime= 1.0324 edges= 9799 schur= 0 lambda= 739.839363 levenbergIter= 1
iteration= 3 chi2= 83834595.145595 time= 0.309102 cumTime= 1.3415 edges= 9799 schur= 0 lambda= 246.613121 levenbergIter= 1
iteration= 4 chi2= 41878079.903257 time= 0.314584 cumTime= 1.65608 edges= 9799 schur= 0 lambda= 82.204374 levenbergIter= 1
iteration= 5 chi2= 16598628.119947 time= 0.306542 cumTime= 1.96263 edges= 9799 schur= 0 lambda= 27.401458 levenbergIter= 1
iteration= 6 chi2= 6137666.739406 time= 0.306009 cumTime= 2.26864 edges= 9799 schur= 0 lambda= 9.133819 levenbergIter= 1
iteration= 7 chi2= 2182986.250589 time= 0.313833 cumTime= 2.58247 edges= 9799 schur= 0 lambda= 3.044606 levenbergIter= 1
iteration= 8 chi2= 732676.668220 time= 0.304348 cumTime= 2.88682 edges= 9799 schur= 0 lambda= 1.014869 levenbergIter= 1
iteration= 9 chi2= 284457.115176 time= 0.305686 cumTime= 3.1925 edges= 9799 schur= 0 lambda= 0.338290 levenbergIter= 1
iteration= 10 chi2= 170796.109734 time= 0.317388 cumTime= 3.50989 edges= 9799 schur= 0 lambda= 0.181974 levenbergIter= 1
iteration= 11 chi2= 145466.315841 time= 0.305792 cumTime= 3.81568 edges= 9799 schur= 0 lambda= 0.060658 levenbergIter= 1
iteration= 12 chi2= 142373.179501 time= 0.347022 cumTime= 4.16271 edges= 9799 schur= 0 lambda= 0.020219 levenbergIter= 1
iteration= 13 chi2= 137485.756901 time= 0.304775 cumTime= 4.46748 edges= 9799 schur= 0 lambda= 0.006740 levenbergIter= 1
iteration= 14 chi2= 131202.175665 time= 0.311505 cumTime= 4.77899 edges= 9799 schur= 0 lambda= 0.002247 levenbergIter= 1
iteration= 15 chi2= 128006.202529 time= 0.30704 cumTime= 5.08603 edges= 9799 schur= 0 lambda= 0.000749 levenbergIter= 1
iteration= 16 chi2= 127587.860945 time= 0.313496 cumTime= 5.39952 edges= 9799 schur= 0 lambda= 0.000250 levenbergIter= 1
iteration= 17 chi2= 127578.599359 time= 0.322269 cumTime= 5.72179 edges= 9799 schur= 0 lambda= 0.000083 levenbergIter= 1
iteration= 18 chi2= 127578.573853 time= 0.326536 cumTime= 6.04833 edges= 9799 schur= 0 lambda= 0.000028 levenbergIter= 1
iteration= 19 chi2= 127578.573840 time= 0.328882 cumTime= 6.37721 edges= 9799 schur= 0 lambda= 0.000018 levenbergIter= 1
iteration= 20 chi2= 127578.573840 time= 0.315369 cumTime= 6.69258 edges= 9799 schur= 0 lambda= 0.000012 levenbergIter= 1
iteration= 21 chi2= 127578.573840 time= 0.308945 cumTime= 7.00152 edges= 9799 schur= 0 lambda= 0.000008 levenbergIter= 1
iteration= 22 chi2= 127578.573840 time= 3.00403 cumTime= 10.0056 edges= 9799 schur= 0 lambda= 296083660142.312988 levenbergIter= 10
saving optimization results ...
可以发现,迭代23次后,总体误差保持不变,事实上可以让优化算法停止。
打开文件result_lie.g2o:
在终端运行:
g2o_viewer result_lie.g2o
运行图为(使用李代数自定义节点与优化后的结果):
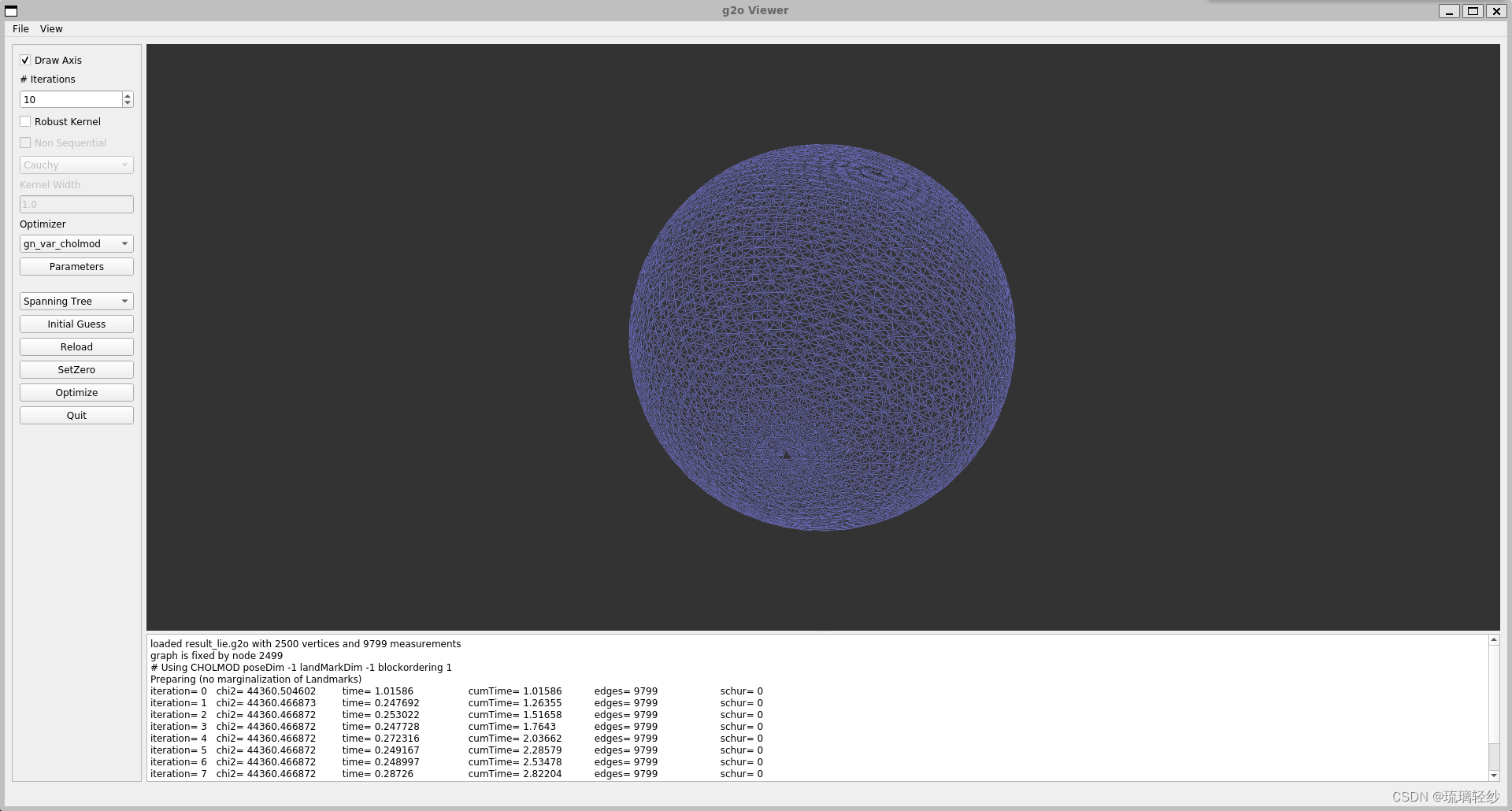
单击窗口中的Optimize按钮,g2o将使用它自带的SE3顶点进行优化,可以在窗口下方的文本框看到以下内容:
loaded result_lie.g2o with 2500 vertices and 9799 measurements
graph is fixed by node 2499
# Using CHOLMOD poseDim -1 landMarkDim -1 blockordering 1
Preparing (no marginalization of Landmarks)
iteration= 0 chi2= 44360.504602 time= 1.01586 cumTime= 1.01586 edges= 9799 schur= 0
iteration= 1 chi2= 44360.466873 time= 0.247692 cumTime= 1.26355 edges= 9799 schur= 0
iteration= 2 chi2= 44360.466872 time= 0.253022 cumTime= 1.51658 edges= 9799 schur= 0
iteration= 3 chi2= 44360.466872 time= 0.247728 cumTime= 1.7643 edges= 9799 schur= 0
iteration= 4 chi2= 44360.466872 time= 0.272316 cumTime= 2.03662 edges= 9799 schur= 0
iteration= 5 chi2= 44360.466872 time= 0.249167 cumTime= 2.28579 edges= 9799 schur= 0
iteration= 6 chi2= 44360.466872 time= 0.248997 cumTime= 2.53478 edges= 9799 schur= 0
iteration= 7 chi2= 44360.466872 time= 0.28726 cumTime= 2.82204 edges= 9799 schur= 0
iteration= 8 chi2= 44360.466872 time= 0.243892 cumTime= 3.06594 edges= 9799 schur= 0
iteration= 9 chi2= 44360.466872 time= 0.245539 cumTime= 3.31148 edges= 9799 schur= 0
3. 遇到的问题及解决办法
3.1 在运行pose_graph_g2o_lie时出现错误
- 出现的错误如下所示:
Sophus ensure failed in function 'void Sophus::SO3Base<Derived>::normalize() [with Derived = Sophus::SO3<double>]', file '/usr/local/include/sophus/so3.hpp', line 273.
Quaternion ( 0.706662 4.32706e-17 0.707551 -4.3325e-17) should not be close to zero!
Aborted
原因:
顶点类VertexSE3LieAlgebra的读入函数virtual bool read(istream& is)缺少返回值,会报以上错误。
解决办法:
在函数 virtual bool read(istream& is) 中加入 return true;