系列文章目录
简介:Computer Graphics From Scratch-《从零开始的计算机图形学》简介
第一章: Computer Graphics From Scratch - Chapter 1 介绍性概念
第二章:Computer Graphics From Scratch - Chapter 2 基本光线追踪
第三章:Computer Graphics From Scratch - Chapter 3 光照
第四章:Computer Graphics From Scratch - Chapter 4 阴影和反射
第五章:Computer Graphics From Scratch - Chapter 5 扩展光线追踪
第六章:Computer Graphics From Scratch - Chapter 6 线条
第七章:Computer Graphics From Scratch - Chapter 7 实心三角形
第八章:Computer Graphics From Scratch - Chapter 8 阴影三角形
Chapter 9
- 系列文章目录
- Perspective Projection - 透视投影
- 一、Basic Assumptions - 基本假设
- 二、Finding P' - 寻找点P'
- 三、The Projection Equation - 投影方程
- 四、Properties of the Projection Equation - 投影方程的性质
- 五、Projecting Our First 3D Object - 投影我们的第一个 3D 对象
- 六、Summary - 概括
Perspective Projection - 透视投影
So far, we have learned to draw 2D triangles on the canvas, given the 2D coordinates of their vertices. However, the goal of this book is to render 3D scenes. So in this chapter, we’ll take a break from 2D triangles and focus on how to turn 3D scene coordinates into 2D canvas
coordinates. We’ll then use this to draw 3D triangles on the 2D canvas.
到目前为止,我们已经学会了在画布上绘制 2D 三角形,给定其顶点的 2D 坐标。
但是,本书的目标是渲染3D场景。因此,在本章中,我们将从 2D 三角形中休息一下,重点介绍如何将 3D 场景坐标转换为 2D 画布坐标。然后,我们将使用它在 2D 画布上绘制 3D 三角形。
一、Basic Assumptions - 基本假设
就像我们在第 2 章开头所做的那样,我们将从定义相机时代开始。 我们将使用与之前相同的约定:
相机位于
O
=
(
0
,
0
,
0
)
O = (0, 0, 0)
O=(0,0,0),看向
Z
+
→
\overset{\rightarrow}{Z_+}
Z+→的方向,它的“向上”向量是
Y
+
→
\overset{\rightarrow}{Y_+}
Y+→。
我们还将定义一个大小为
V
w
V_w
Vw 和
V
h
V_h
Vh 的矩形视口 (viewport) ,其边缘平行于
X
→
\overset{\rightarrow}{X}
X→ 和
Y
→
\overset{\rightarrow}{Y}
Y→,距离相机
d
d
d 。
目标是在画布上绘制任何东西相机通过视口看到。 如果您需要复习这些概念,请参阅第 2 章。
考虑相机前方某处的
P
P
P点。我们感兴趣的是找到
P
′
P^′
P′,即摄像机在视口上看到
P
P
P 的点,如图 9-1 所示。

图 9-1:简单的透视投影设置。相机看到投影平面上的P到P’。
这与我们对光线追踪所做的相反。
我们的光线追踪器从画布上的一个点开始,并确定它可以通过该点看到什么;
在这里,我们从场景中的某个点开始,并希望确定它在视口上的可见位置。
二、Finding P’ - 寻找点P’
要找到
P
′
P′
P′ ,让我们从字面上从不同的角度看图 9-1 中所示的设置。
图 9-2 显示了从“右侧”查看的设置图,就好像我们站在
X
⃗
\vec{X}
X 轴上一样:
Y
+
⃗
\vec{Y_+}
Y+ 指向上方,
Z
+
⃗
\vec{Z_+}
Z+ 指向右侧,
X
+
⃗
\vec{X_+}
X+指向我们。

图 9-2:从右侧查看的透视投影设置
除了 O O O、 P P P 和 P ′ P^′ P′ 之外,这张图还显示了点 A A A 和 B B B,这有助于我们推理它。
我们知道
P
z
′
=
d
P^′_z = d
Pz′=d,因为我们将
P
′
P^′
P′ 定义为视口上的一个点,并且我们知道视口嵌入在平面
Z
=
d
Z = d
Z=d 中。
我们还可以看到三角形 OP’A 和 OPB 是相似的,因为它们对应的边(P′A 和 PB、OP 和 OP′、OA 和 OB)是平行的。这意味着它们侧面的比例是相同的;
例如:
∣ P ′ A ∣ ∣ O A ∣ = ∣ P B ∣ ∣ O B ∣ \dfrac{|P'A|}{|OA|} = \dfrac{|PB|}{|OB|} ∣OA∣∣P′A∣=∣OB∣∣PB∣
由此,我们得到
∣
P
′
A
∣
=
∣
P
B
∣
⋅
∣
O
A
∣
∣
O
B
∣
|P'A| = \dfrac{|PB| \cdot |OA|}{|OB|}
∣P′A∣=∣OB∣∣PB∣⋅∣OA∣
该等式中每个段的(有符号)长度是我们知道或我们感兴趣的点的坐标:
∣
P
′
A
∣
=
P
y
′
|P^′ A|= P^′_y
∣P′A∣=Py′,
∣
P
B
∣
=
P
y
|PB|= P_y
∣PB∣=Py,
∣
O
A
∣
=
P
z
′
=
d
|OA|= P^′_z = d
∣OA∣=Pz′=d, 和
∣
O
B
∣
=
P
z
|OB|= P_z
∣OB∣=Pz。
如果我们在等式中替换这些,我们得到
P y ′ = P y ⋅ d P z P'_y = \dfrac{P_y \cdot d}{P_z} Py′=PzPy⋅d
我们可以绘制一个类似的图,这次从上方查看设置:
Z
+
⃗
\vec{Z_+}
Z+ 点向上,
X
+
⃗
\vec{X_+}
X+ 指向右侧,
Y
+
⃗
\vec{Y_+}
Y+ 指向我们(图9-3)。
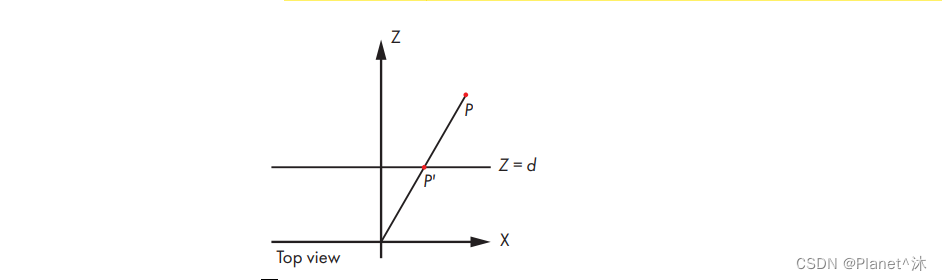
图 9-3:透视的俯视图投影设置
以相同的方式再次使用类似的三角形,我们可以推断出:
P
x
′
=
P
x
⋅
d
P
z
P'_x = \dfrac{P_x \cdot d}{P_z}
Px′=PzPx⋅d
我们现在拥有
P
′
P'
P′ 的所有三个坐标。
三、The Projection Equation - 投影方程
让我们把所有这些放在一起。
给定场景中的点 P 以及标准的摄像机和视口设置,我们可以计算 P 在视口上的投影,我们称之为 P′,如下所示:
P
x
′
=
P
x
⋅
d
P
z
P'_x = \dfrac{P_x \cdot d}{P_z}
Px′=PzPx⋅d
P
y
′
=
P
y
⋅
d
P
z
P'_y = \dfrac{P_y \cdot d}{P_z}
Py′=PzPy⋅d
P
z
′
=
d
P'_z = d
Pz′=d
P′ 位于视口上,但它仍然是 3D 空间中的一个点。我们如何在画布中获得相应的点?
我们可以立即删除
P
z
′
P'_z
Pz′,因为每个投影点都在视口平面上。
接下来,我们需要将
P
x
′
P'_x
Px′ 和
P
y
′
P'_y
Py′ 转换为画布坐标
C
x
C_x
Cx和
C
y
C_y
Cy。
P
′
P'
P′ 仍然是场景中的一个点,因此其坐标以场景单位表示。
我们可以将它们除以视口的宽度和高度。这些也以场景单位表示,因此我们获得临时无单位的值。
最后,我们将它们乘以画布的宽度和高度,以像素表示:
C
x
=
P
x
′
⋅
C
w
V
w
C_x = \dfrac{P'_x \cdot C_w}{V_w}
Cx=VwPx′⋅Cw
C y = P y ′ ⋅ C h V h C_y = \dfrac{P'_y \cdot C_h}{V_h} Cy=VhPy′⋅Ch
这种视口到画布的变换与我们在本书光线追踪部分使用的画布到视口变换完全相反。有了这个,我们终于可以从场景中的一个点变成屏幕上的像素了!
四、Properties of the Projection Equation - 投影方程的性质
在我们继续之前,投影有一些有趣的属性值得讨论的方程式。
上面的方程式应该与我们看待现实世界事物的日常经验兼容。
例如,物体离得越远,它看起来越小;事实上,如果我们增加
P
z
P_z
Pz,我们会变小
P
x
′
P'_x
Px′和
P
y
′
P'_y
Py′的值。
然而,当我们过多地降低 P z P_z Pz的值时,事情就不再那么直观了;
对于 P z P_z Pz 的负值,即当一个物体在相机后面时,物体仍然被投影,但颠倒了!
当然,当 P z = 0 P_z = 0 Pz=0 时,我们将除以零,宇宙就会内爆。
我们需要找到一种方法来避免这些不愉快的情况; 现在,我们假设每个点都在镜头前,并在后面的章节中处理。
透视投影的另一个基本属性是它保持点对齐:
如果三个点在空间中对齐,它们的投影将在视口上对齐。
换句话说,直线总是被投影为直线。 这听起来太明显而不值得一提,但请注意,例如,两条线之间的角度并没有保持不变;
在现实生活中,我们看到平行线在地平线上“汇合”,例如在高速公路上行驶时。
直线总是被投影为直线这一事实对我们来说非常方便:到目前为止我们谈论的是投影一个点,但是如何投影一条线段,甚至是一个三角形呢?
由于这个性质,两点之间的线段投影就是两点投影之间的线段;
三角形的投影是由其顶点的投影形成的三角形。
五、Projecting Our First 3D Object - 投影我们的第一个 3D 对象
这意味着我们可以继续绘制我们的第一个 3D 对象:立方体。
我们定义它的 8 个顶点的坐标,并在构成立方体边的 12 对顶点的投影之间绘制线段,如示例 9-1 所示。
ViewportToCanvas(x, y) {
return (x * Cw/Vw, y * Ch/Vh);
}
ProjectVertex(v) {
return ViewportToCanvas(v.x * d / v.z, v.y * d / v.z)
}
// The four "front" vertices
vAf = [-1, 1, 1]
vBf = [ 1, 1, 1]
vCf = [ 1, -1, 1]
vDf = [-1, -1, 1]
// The four "back" vertices
vAb = [-1, 1, 2]
vBb = [ 1, 1, 2]
vCb = [ 1, -1, 2]
vDb = [-1, -1, 2]
// The front face
DrawLine(ProjectVertex(vAf), ProjectVertex(vBf), BLUE);
DrawLine(ProjectVertex(vBf), ProjectVertex(vCf), BLUE);
DrawLine(ProjectVertex(vCf), ProjectVertex(vDf), BLUE);
DrawLine(ProjectVertex(vDf), ProjectVertex(vAf), BLUE);
// The back face
DrawLine(ProjectVertex(vAb), ProjectVertex(vBb), RED);
DrawLine(ProjectVertex(vBb), ProjectVertex(vCb), RED);
DrawLine(ProjectVertex(vCb), ProjectVertex(vDb), RED);
DrawLine(ProjectVertex(vDb), ProjectVertex(vAb), RED);
// The front-to-back edges
DrawLine(ProjectVertex(vAf), ProjectVertex(vAb), GREEN);
DrawLine(ProjectVertex(vBf), ProjectVertex(vBb), GREEN);
DrawLine(ProjectVertex(vCf), ProjectVertex(vCb), GREEN);
DrawLine(ProjectVertex(vDf), ProjectVertex(vDb), GREEN);
Listing 9-1: Drawing a cube
We get something like Figure 9-4 .
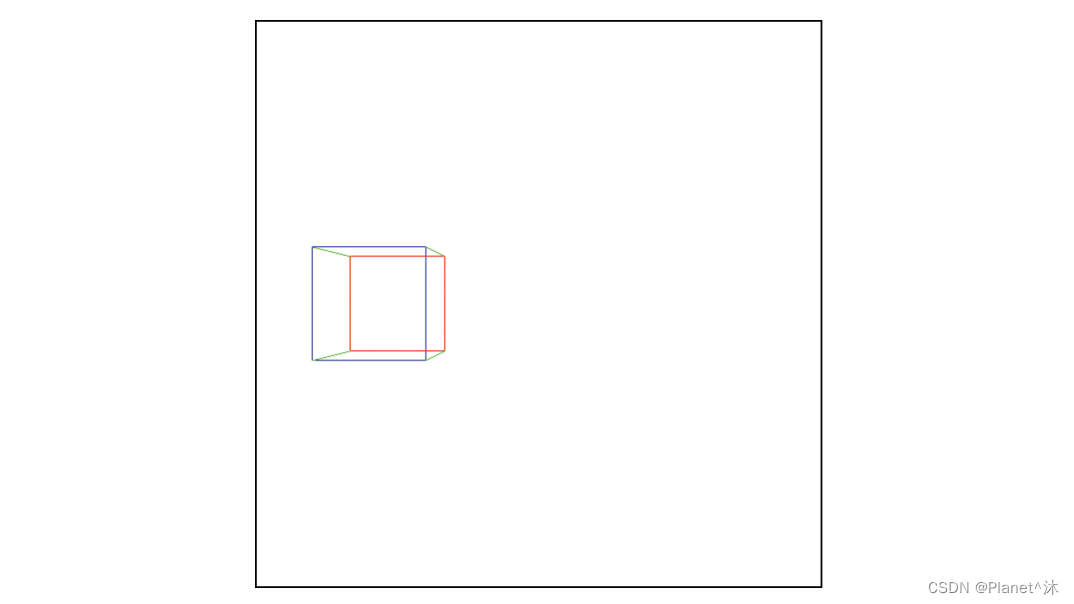
Figure 9-4: Our first 3D object projected on a 2D canvas: a cube
You can find a live implementation of this algorithm at
https://gabrielgambetta.com/cgfs/perspective-demo.
我们已经成功地从物体的几何3D表示转变为从我们的合成相机看到的2D表示!
不过,我们的方法是非常手工的。它有许多局限性。如果我们想渲染两个立方体呢?我们必须复制大部分代码吗?如果我们想渲染立方体以外的东西,该怎么办?如果我们想让用户从文件中加载三维模型,该怎么办?我们显然需要一种更加数据驱动的方法来表示3D几何。
六、Summary - 概括
在本章中,我们开发了从场景中的3D点到画布上的2D点的数学方法。由于透视投影的特性,我们可以立即将其扩展到投影线段,然后扩展到三维对象。
但我们还有两个重要问题没有解决。首先,示例9-1将透视投影逻辑与立方体的几何体混合在一起;这种方法显然不会扩大规模。其次,由于透视投影方程的限制,它无法处理相机后面的物体。我们将在接下来的两章中讨论这些问题。