目录
前言:
二叉树遍历方式:
手撕前中后序遍历(递归)的三大准备
深度优先搜索:
手撕前中后遍历(递归):
手撕前中后序遍历(迭代):
深度优先搜索:
总结:
前言:
今天我们将带领大家手撕二叉树的遍历,本篇会分别讲解深度优先搜索法和广度优先有搜索法下的各自详细算法,大家做好准备了嘛?
二叉树遍历方式:
- 深度优先遍历
- 广度优先遍历
手撕前中后序遍历(递归)的三大准备
- 确定递归函数的参数和返回值。
- 确定终止条件。
- 确定单层递归的逻辑。
深度优先搜索:
手撕前中后遍历(递归):
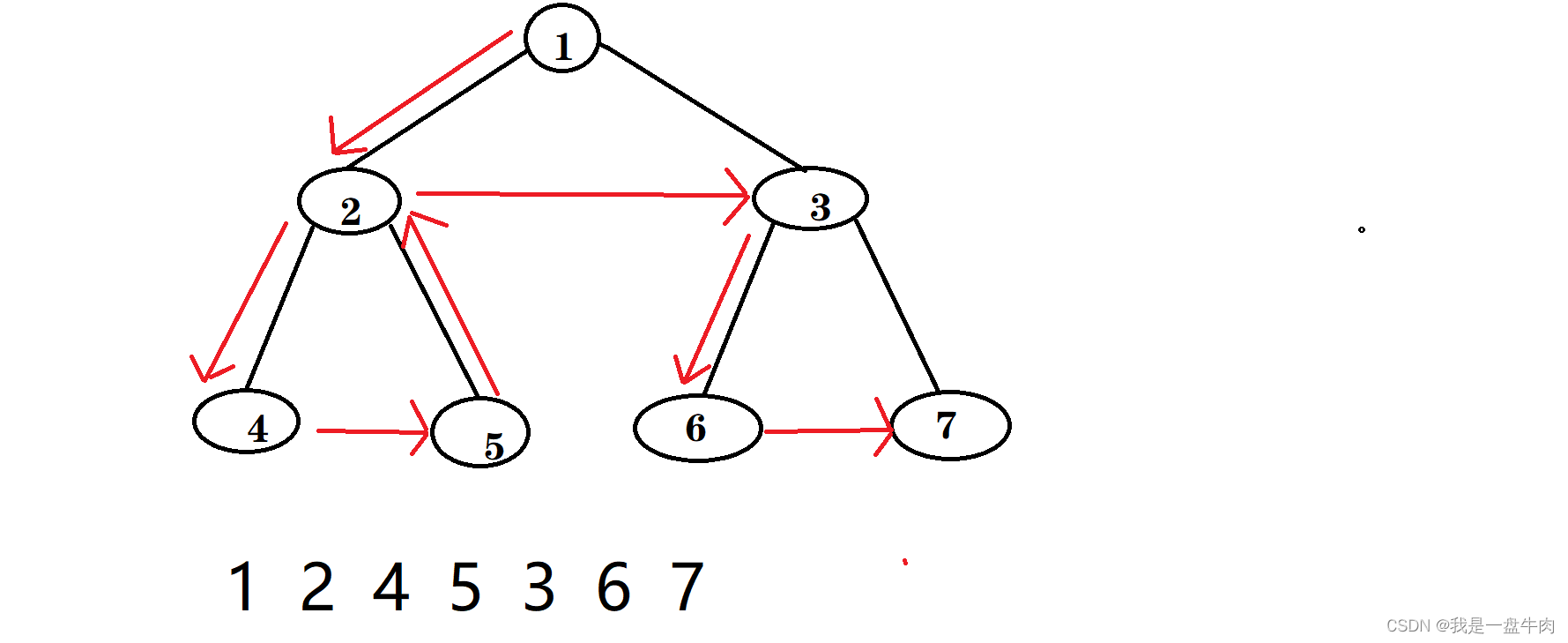
讲深度优先搜索遍历,实际上就是在讲前中后序遍历的方法,我们先用前序遍历进行讲解。
1.确定递归函数的参数和返回值:我们就只传递一个节点以及存储遍历结果用的vector容器就可以了。
void traversal(TreeNode* cur, vector<int>& vec)
2.确定终止条件:在递归的时候,如果下层没有节点,那么就证明我们此时已经遍历到最底层了,就要返回,也就是如果这个节点为空节点,我们就要终止递归。
if (cur == NULL) return;
3.确定单层递归的逻辑:前序遍历是中左右的循序,所以在单层递归的逻辑,是要先取中节点的数值,代码如下:
vec.push_back(cur->val); // 中
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
单层递归的逻辑就是按照中左右的顺序来处理的,这样二叉树的前序遍历,基本就写完了。其实整体的逻辑还是比较简单的:
我们最开始把 1 传递进去,此时节点不为空,说明 1 节点实际存在,就把 1 存储到数组里面,之后我们把1的左右子节点分别再传入进去,反复进行 1 节点经历的操作,循环往复就完成了整个树的遍历
完整核心代码:
class Solution {
public:
void findallnodes(TreeNode* node ,vector<int>& d1)
{
if (node == NULL) return;
d1.push_back(node->val);
findallnodes(node->left,d1);
findallnodes(node->right,d1);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int>result;
findallnodes(root,result);
return result;
}
};其实中序遍历和后序遍历的逻辑都和前序遍历一样,就是数据在存储的时候要有所改动
中序遍历:
traversal(cur->left, vec); // 左
vec.push_back(cur->val); // 中
traversal(cur->right, vec); // 右
后序遍历:
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
vec.push_back(cur->val); // 中手撕前中后序遍历(迭代):
迭代法实际上是用栈来模拟递归的过程。
前序遍历:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // 中
st.pop();
result.push_back(node->val);
if (node->right) st.push(node->right); // 右(空节点不入栈)
if (node->left) st.push(node->left); // 左(空节点不入栈)
}
return result;
}
};详细解释:
这是一个二叉树的前序遍历算法的实现。算法的核心思想是使用栈来模拟递归遍历,具体步骤如下:
- 新建一个空栈st和一个空向量result;
- 若二叉树根节点为空,直接返回结果result;
- 将二叉树根节点压入栈中;
- 取出当前栈顶元素node,并将node的值加入result向量中;
- 若node的右子节点不为空,将右子节点压入栈中;
- 若node的左子节点不为空,将左子节点压入栈中;
- 重复步骤(4)-(6),直到栈为空;
- 返回向量result。
在实现过程中需要注意的是,因为前序遍历的顺序是根节点-左子树-右子树,所以需要先将右子节点入栈,再将左子节点入栈,才能保证取出栈顶元素时先访问左子树。另外,注意判断节点是否为空,为空时不需要入栈遍历。
中序遍历:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur != NULL || !st.empty()) {
if (cur != NULL) { // 指针来访问节点,访问到最底层
st.push(cur); // 将访问的节点放进栈
cur = cur->left; // 左
} else {
cur = st.top(); // 从栈里弹出的数据,就是要处理的数据(放进result数组里的数据)
st.pop();
result.push_back(cur->val); // 中
cur = cur->right; // 右
}
}
return result;
}
};
这是一个二叉树的中序遍历算法的实现。该算法使用栈来模拟递归遍历,具体步骤如下:
1. 新建一个空向量result和一个空栈st,同时初始化一个指针cur指向二叉树的根节点;
2. 当当前指针cur不为空或栈st不为空时,执行下列操作:
a. 若当前指针cur不为空,则将该节点加入栈st中,并将指针cur指向其左子节点,相当于递归遍历到左子树的最底层;
b. 否则,即当前节点已经访问到最底层,从栈中将其弹出,并将其加入到结果向量result中,并将指针cur指向当前节点的右子节点,相当于返回到上一层节点继续遍历右子树;
3. 重复步骤2,直到指针cur为空且栈st为空;
4. 返回结果向量result。
在实现过程中,需要注意的是,由于中序遍历的顺序是左子树-根节点-右子树,所以需要先将整个左子树压入栈中,从栈中弹出的节点即为左子树最底层节点的父节点,并且该节点的左子树已经访问完毕,接下来需要访问该节点,并将指针cur指向右子节点,以此类推。另外,要注意判断节点是否为空,为空时不需要入栈和处理。
后序遍历:
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
if (node->left) st.push(node->left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)
if (node->right) st.push(node->right); // 空节点不入栈
}
reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
return result;
}
};这是一个二叉树的后序遍历算法的实现。该算法使用栈来模拟递归遍历,具体步骤如下:
- 新建一个空栈st和一个空向量result;
- 若二叉树根节点为空,直接返回结果result;
- 将二叉树根节点压入栈中;
- 取出当前栈顶元素node,并将node的值加入result向量中;
- 若node的左子节点不为空,将左子节点压入栈中;
- 若node的右子节点不为空,将右子节点压入栈中;
- 重复步骤(4)-(6),直到栈为空;
- 返回向量result,并将其反转,得到左右中的顺序。
在实现过程中需要注意的是,由于后序遍历的顺序是左子树-右子树-根节点,所以需要先访问左子节点和右子节点,最后再访问根节点,即将左子节点和右子节点的遍历顺序颠倒,然后将结果向量反转即可得到左右中的顺序。另外,需要注意判断节点是否为空,为空时不需要入栈遍历。
深度优先搜索:
层序遍历:
就是把二叉树中的数据一层一层的保存。
迭代法实现:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
};这是一个二叉树的层序遍历算法的实现,即按照树的层次依次输出各节点的值。该算法使用队列来实现,具体步骤如下:
1. 新建一个空队列que,将根节点加入队列中;
2. 初始化一个空二维向量result,用于存储节点的值;
3. 当队列非空时,执行下列操作:
a. 获取当前队列元素的个数size,表示当前层的节点个数;
b. 新建一个空向量vec,用于存储当前层的节点值;
c. 依次从队列中取出元素,并将其值加入到vec中,并将其左右子节点加入队列中;
d. 将vec加入到result中;
4. 返回result向量,其中每个子向量表示一层的节点值。
在实现过程中,需要注意的是,在每一层遍历完成之后,需要将该层节点的值加入到二维向量result中。由于是按照层次遍历,因此需要保证同一层的节点先加入队列中,才能在后续的遍历中获取到该层节点的值。
递归法实现:
class Solution {
public:
void order(TreeNode* cur, vector<vector<int>>& result, int depth)
{
if (cur == nullptr) return;
if (result.size() == depth) result.push_back(vector<int>());
result[depth].push_back(cur->val);
order(cur->left, result, depth + 1);
order(cur->right, result, depth + 1);
}
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
int depth = 0;
order(root, result, depth);
return result;
}
};这是一个二叉树的层序遍历算法的实现,与上一个算法不同的是,该算法采用递归实现。具体步骤如下:
1. 新建一个空二维向量result、一个初始深度depth为0的变量,并将根节点root作为当前节点cur;
2. 递归遍历当前节点cur的左子树和右子树,同时传递当前层的result二维向量和深度depth+1;
3. 将当前节点cur的值加入到result中对应深度的子向量中;
4. 当result中没有深度为depth的子向量时,新建一个空向量并加入到result中;
5. 返回result向量即可。
在实现过程中,需要注意的是,每个节点所在的深度取决于它的父节点深度,因此在递归遍历时深度depth需要加1。递归结束条件为当前节点cur为空。因为在递归遍历左子树和右子树之前,需要先将当前节点加入到result中对应深度的子向量中,因此result的初始值应为空。
总结:
本篇详细的介绍了手撕二叉树遍历的各种常见方式,只有熟练的掌握树的遍历方式,我们才可以更加熟练的使用各种树结构,狠狠的拿下数据结构与算法。
如果我的内容对你有帮助,请点赞,评论,收藏。创作不易,大家的支持就是我坚持下去的动力!



![[电离层建模学习笔记]开源程序M_GIM学习记录](https://img-blog.csdnimg.cn/a5dbf218614f43938b6ff855254bc6ed.png)