一.模式匹配
字符串的模式匹配算法是用来查找一个字符串中是否存在另一个指定的字符串(即模式)的算法。常见的模式匹配算法包括暴力匹配算法、KMP算法、Boyer-Moore算法和Rabin-Karp算法。
- 暴力匹配算法:暴力匹配算法也称为朴素匹配算法,是最简单的一种字符串匹配算法。它从主串的第一个字符开始与模式串的第一个字符比较,如果相同,则继续比较后面的字符,直到发现不匹配的字符或者模式串完全匹配主串为止。
- KMP算法:KMP算法是由Knuth-Morris-Pratt三位作者共同提出的一种高效的字符串匹配算法。其核心思想是利用已经匹配过的信息,尽量减少无用的比较次数。具体实现方式是构建一个next数组,记录模式串中每个前缀子串的最长公共前后缀长度,然后根据next数组跳过一些已经匹配的字符,使得模式串移动的更加快速。
- Boyer-Moore算法:Boyer-Moore算法是由Robert S. Boyer和J Strother Moore在1977年提出的一种高效的字符串匹配算法。它通过预处理模式串中每个字符在模式串中出现的位置以及根据坏字符和好后缀规则来决定跳过多少个字符,以达到快速匹配的目的。
- Rabin-Karp算法:Rabin-Karp算法是由Richard M. Karp和Michael O. Rabin在1987年提出的一种基于哈希函数的字符串匹配算法。它利用哈希函数对主串和模式串进行哈希计算,并比较哈希值是否相等,从而判断是否匹配。同时,由于哈希函数具有良好的性质,可以在实际应用中获得较高的效率。
在我们考研408范围内需要掌握的也就是第一种暴力匹配算法和KMP匹配算法,今天我们重点来实现这两种算法。
二.暴力匹配算法
1.原理
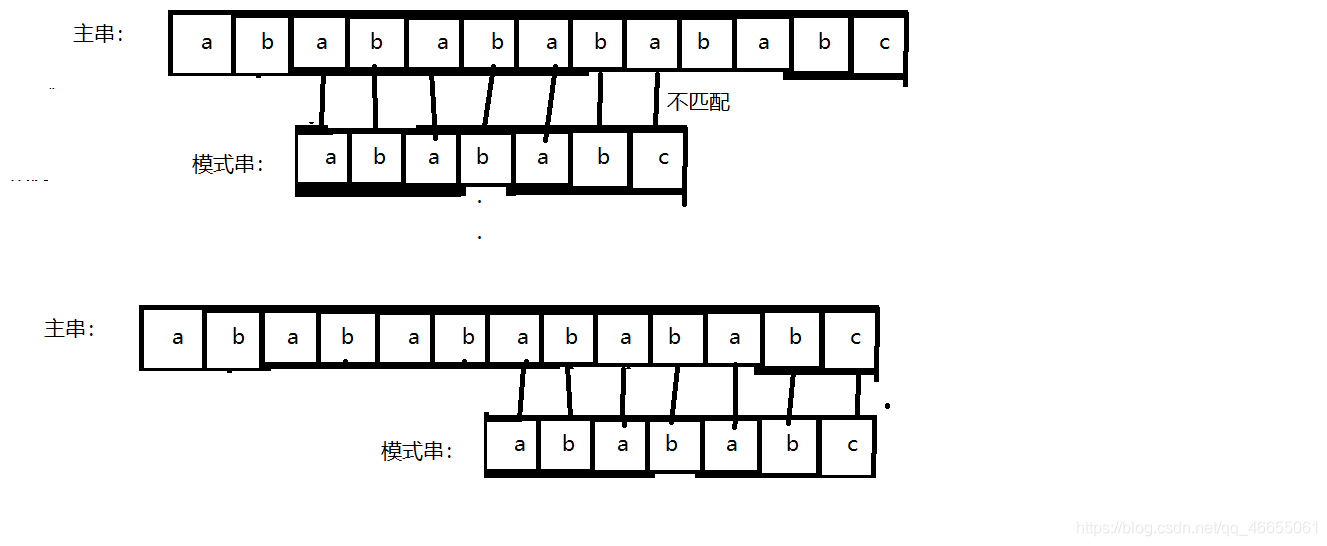
暴力匹配算法的原理非常简单,它从主串的第一个字符开始,与模式串的第一个字符进行比较,如果相同,则继续比较主串和模式串的下一个字符。如果出现不匹配的情况,则将主串中的指针后移一位,重新从主串的下一个位置开始与模式串进行比较。
具体来说,暴力匹配算法的过程如下:
- 从主串的第一个字符开始,与模式串的第一个字符进行比较;
- 如果相同,则继续比较主串和模式串的下一个字符,直到模式串遍历完毕,返回匹配成功;
- 如果出现不匹配的情况,则将主串中的指针后移一位,重新从主串的下一个位置开始与模式串进行比较,直到主串遍历完毕。如果仍然没有找到匹配的子串,则返回匹配失败。
因为暴力匹配算法是一种最简单的字符串匹配算法,所以它的时间复杂度比较高,平均需要O(mn)次比较操作才能完成匹配,其中m和n分别表示模式串和主串的长度。但是,它也有一些优点,例如实现简单,代码易于理解和调试,适用于小规模的字符串匹配问题等。
2.示意图
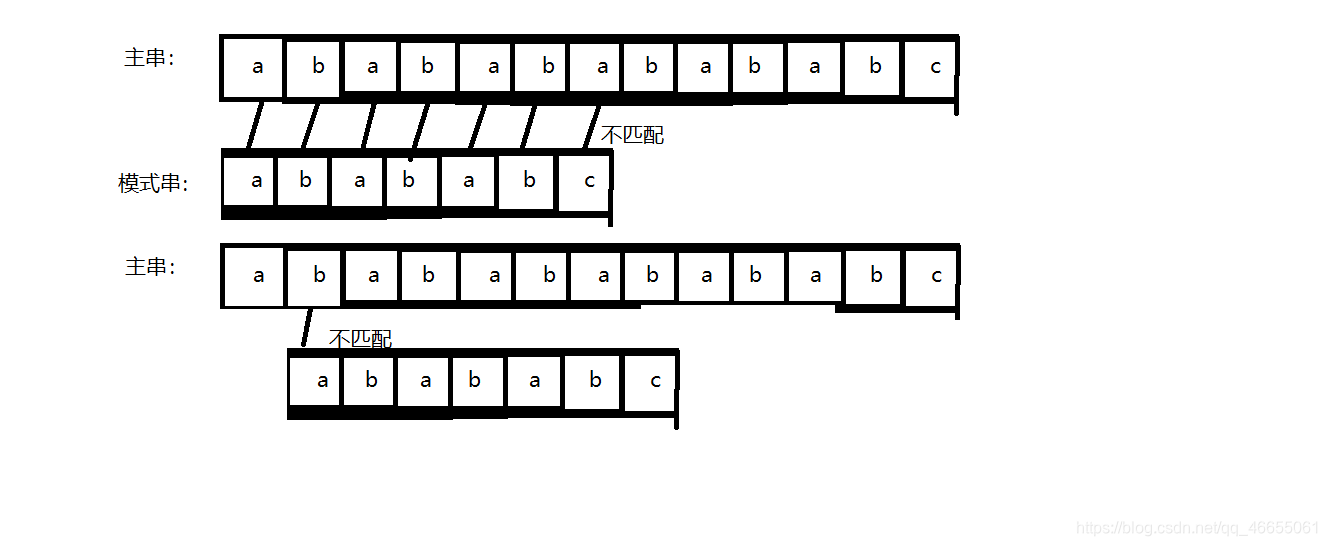
3.C语言算法代码
//暴力匹配算法
int force_search(SString S,SString T){ //第一个字符串为主串,而第二个字符串为模式串
int i=1,j=1; //为了好匹配,让字符串从1开始,0的位置存储长度
while(i<=S.length && j<=T.length){
if(S.val[i]==T.val[j]){ //匹配到了第一个,继续向下匹配
++i;
++j;
}
else{
i=i-j+2; //指针回退重新匹配,这个代数式来源于笔算验证
j=1;
}
}
if(j>T.length)
return i-T.length; //匹配成功直至最后一位的下一位,j超出T的长度而i减去T的长度刚好就是匹配起始位置
else
return 0; //不成功为了程序继续进行就输出0,我们认为知道匹配不成功就行
}
三.KMP匹配算法
1.原理
KMP算法的核心思想是在匹配过程中尽量利用已经匹配过的信息,从而减少比较次数。具体来说,它通过构建一个next数组,记录模式串中每个前缀子串的最长公共前后缀长度,然后根据next数组跳过一些已经匹配的字符,使得模式串移动的更加快速。
KMP算法的过程如下:
- 预处理:首先,我们需要构造出模式串p的next数组,用于保存模式串中每个前缀子串的最长公共前后缀长度。具体来说,从模式串的第二个位置开始,依次计算每个位置对应的next值:
(1)如果前缀的第一个字符和后缀的最后一个字符相等,则next值为前一个位置的next值+1; (2)如果前缀的第一个字符和后缀的最后一个字符不相等,或者已经没有前缀可以继续匹配了,则next值为0。
- 匹配:在匹配过程中,我们将主串s和模式串p的指针都初始化为0,然后依次比较它们的对应字符:
(1)如果当前字符匹配,则分别将指针后移一位,继续比较下一个字符; (2)如果当前字符不匹配,则根据next数组将模式串向右移动若干位,直到匹配或者模式串已经全部移动完成。
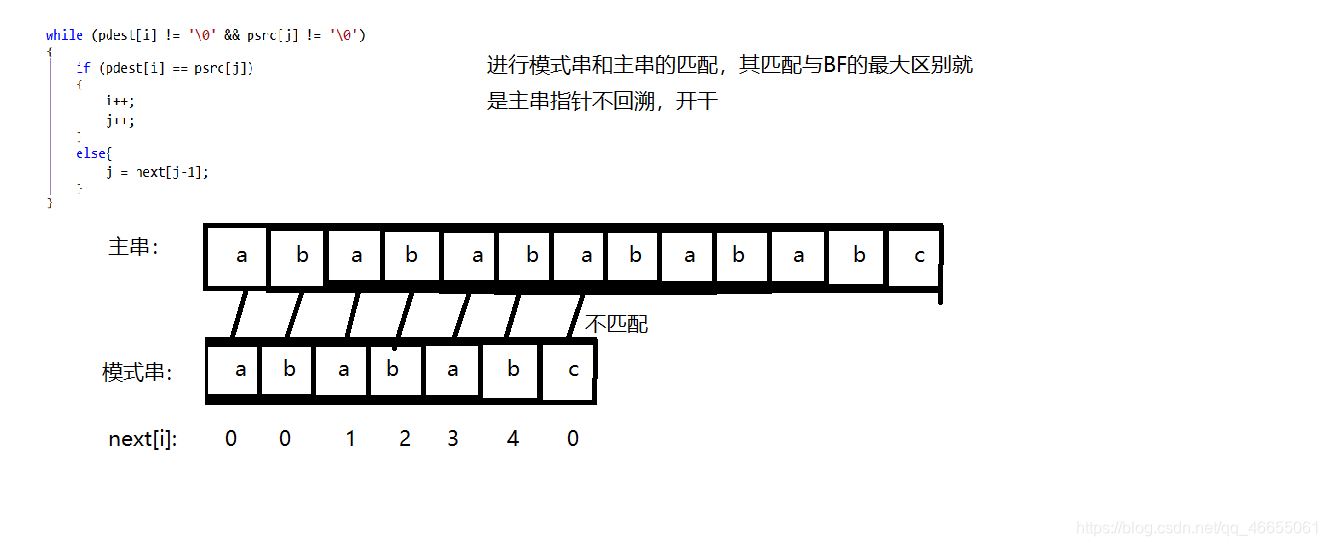
在KMP算法中,模式串的移动是根据next数组进行的。具体来说,当模式串中第j个字符与主串中第i个字符不匹配时,我们可以将模式串向右移动max(j-next[j],1)个位置,然后重新开始比较。这样,就能够充分利用已经匹配过的信息,避免重复比较。
总的来说,KMP算法的时间复杂度为O(m+n),其中m和n分别表示模式串和主串的长度。虽然KMP算法需要预处理出next数组,但是它对于稍大规模的字符串匹配问题具有较高的效率和较好的性能表现。
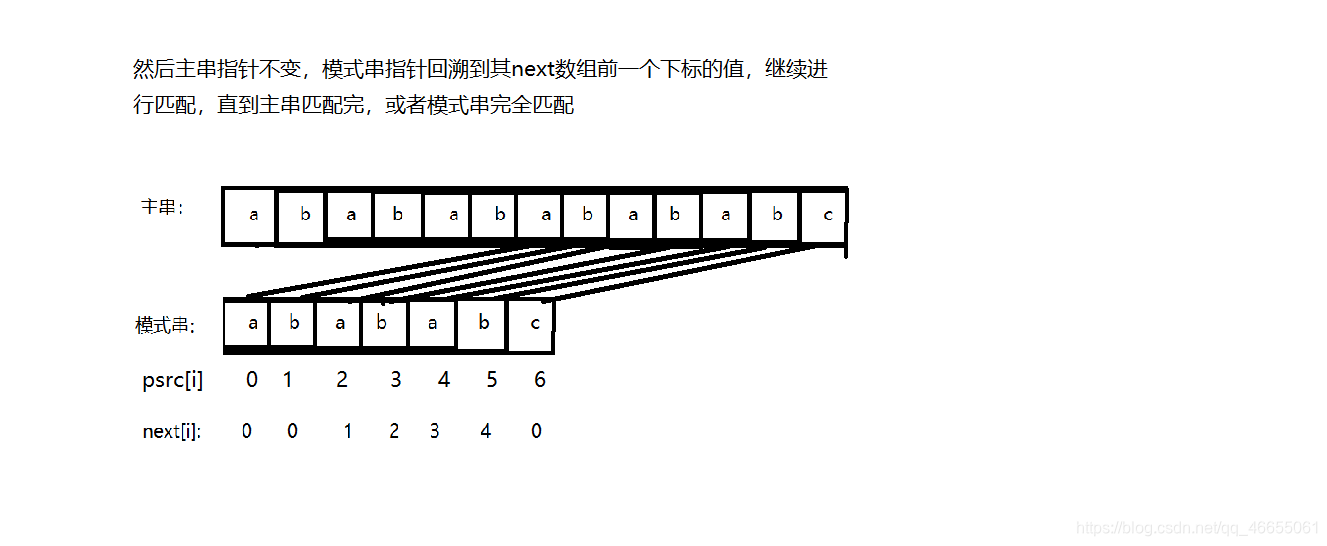
2.示意图
3.优化思路
KMP算法的优化主要有两个方面:
- 改进next数组的求法
传统的KMP算法中,next数组是通过暴力枚举前缀后缀来求解的,时间复杂度为O(m^2),其中m为模式串的长度。实际上,我们可以通过观察next数组的递推公式,发现next[j]的值与next[j-1]的值有关,因此可以通过递推求解next数组,时间复杂度为O(m)。
- 优化跳转操作
在匹配失败时,KMP算法通过next数组来确定新的匹配位置。然而,实际上我们可以通过分析next数组的定义,发现在某些情况下可以直接跳过一段字符,而不需要像传统的KMP算法那样只跳过一个字符。具体而言,如果s[i]!=p[j],且j>0,则可以直接将j跳转到next[j],而不是next[j-1]。
四.核心功能
1.求next数组
//求next数组
void get_next(SString T,int next[]){ //T是模式串
int i=0,j=0; //i用来表示当前匹配到的位置,j用来表示已经匹配好的最长前缀的末尾
next[1]=0; //next[0]不管,next[1]都是0
while(i<T.length){
if(j==0 || T.val[i]==T.val[j]){
++i;
++j;
next[i]=j;
}
else
j=next[j];
}
}
/*这个部分一定要会手算*/
2.求nextval数组
void get_nextval(SString T,int nextval[]){
int i=0,j=0; //i用来表示当前匹配到的位置,j用来表示已经匹配好的最长前缀的末尾
nextval[1]=0; //next[0]不管,next[1]都是0
while(i<T.length){
if(j==0 || T.val[i]==T.val[j]){
++i;
++j;
if(T.val[i]!=T.val[j])
nextval[i]=j;
else
nextval[i]=nextval[j];
}
else
j=nextval[j];
}
}
3.KMP匹配
//KMP匹配算法
int KMP_search(SString S,SString T,int next[]){
int i=1,j=1;
while(i<=S.length && j<=T.length){ //修改循环条件,保证i和j都不超出字符串长度范围
if(j==0 || S.val[i] == T.val[j]){
++i;++j; //匹配到了第一个,继续匹配
}
else{
j=next[j]; //匹配失败后,模式串向右移动,i指针不动
}
}
if(j>T.length) { //这一部分和暴力匹配一样
return i-T.length;
}
else {
return 0;
}
}
五.完整代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXLEN 255
/*数据结构与算法中,常用的模式匹配算法包括暴力匹配算法和KMP匹配算法,今天在这里我们两个都尝试一下*/
//定义串的结构体
typedef struct SString{
char val[MAXLEN];
int length;
}SString;
//暴力匹配算法
int force_search(SString S,SString T){ //第一个字符串为主串,而第二个字符串为模式串
int i=1,j=1; //为了好匹配,让字符串从1开始,0的位置存储长度
while(i<=S.length && j<=T.length){
if(S.val[i]==T.val[j]){ //匹配到了第一个,继续向下匹配
++i;
++j;
}
else{
i=i-j+2; //指针回退重新匹配,这个代数式来源于笔算验证
j=1;
}
}
if(j>T.length)
return i-T.length; //匹配成功直至最后一位的下一位,j超出T的长度而i减去T的长度刚好就是匹配起始位置
else
return 0; //不成功为了程序继续进行就输出0,我们认为知道匹配不成功就行
}
//求next数组
void get_next(SString T,int next[]){ //T是模式串
int i=0,j=0; //i用来表示当前匹配到的位置,j用来表示已经匹配好的最长前缀的末尾
next[1]=0; //next[0]不管,next[1]都是0
while(i<T.length){
if(j==0 || T.val[i]==T.val[j]){
++i;
++j;
next[i]=j;
}
else
j=next[j];
}
}
/*这个部分一定要会手算*/
void get_nextval(SString T,int nextval[]){
int i=0,j=0; //i用来表示当前匹配到的位置,j用来表示已经匹配好的最长前缀的末尾
nextval[1]=0; //next[0]不管,next[1]都是0
while(i<T.length){
if(j==0 || T.val[i]==T.val[j]){
++i;
++j;
if(T.val[i]!=T.val[j])
nextval[i]=j;
else
nextval[i]=nextval[j];
}
else
j=nextval[j];
}
}
//KMP匹配算法
int KMP_search(SString S,SString T,int next[]){
int i=1,j=1;
while(i<=S.length && j<=T.length){ //修改循环条件,保证i和j都不超出字符串长度范围
if(j==0 || S.val[i] == T.val[j]){
++i;++j; //匹配到了第一个,继续匹配
}
else{
j=next[j]; //匹配失败后,模式串向右移动,i指针不动
}
}
if(j>T.length) { //这一部分和暴力匹配一样
return i-T.length;
}
else {
return 0;
}
}
int main(){
//初始化主串
SString S,T;
strcpy(S.val,"abcdefgabclmnzwxyzabcz");
S.length=strlen(S.val); //C语言不像python可以直接赋值,他需要strcpy函数过渡
//初始化模式串
strcpy(T.val,"abcz");
T.length=strlen(T.val);
//暴力搜索
int pos1=force_search(S,T);
printf("Force search result: %d\n",pos1);
//KMP匹配搜索
int next[T.length+1];
int nextval[T.length+1];
get_next(T,next);
get_nextval(T,nextval);
int pos2=KMP_search(S,T,nextval);
printf("KMP search result: %d\n",pos2);
return 0;
}
六.运行结果
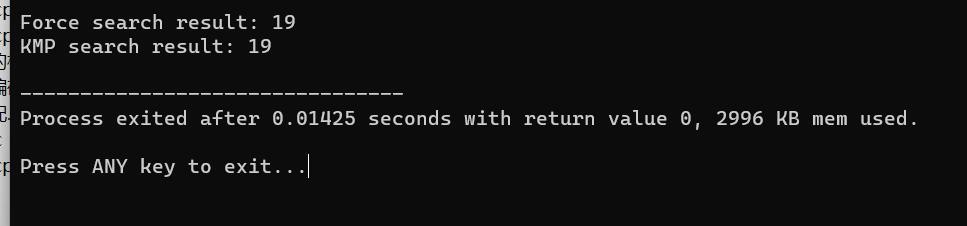
实验结果与我们手算一致。
本次博客主要基于博主之前在CSDN平台的发布问答,根据采纳的答案进行学习总结。
有兴趣的可以前往查看原文回答KMP匹配算法