动态规划算法（多状态dp1）

news2024/11/20 14:40:00

动态规划算法专辑之多状态dp问题（1）

一、什么是多状态

多状态dp问题，指一个规模问题下存在多种状态，我们需要联合关注多种状态间的相互转移，才可以求解目的问题。

多状态问题可以理解为有限状态机，在有限的状态中转换，解决这类问题最重要的就是画出状态转移图

二、最佳买卖股票时机含冷冻期

1.题目解析

针对于题目给的test case有如下分析：

2.状态定义

根据经验+题目要求，dp[i]可以表示为：以i为结尾时的最大利润

和斐波那契数列子问题分析一样，对于斐波那契来说，相减后的值会有多个，而这是有多种状态可能会导致一样dp[i]，因此算出来的dp[i]是无法知道之前的状态的，也就是不确定的，因此我们对于该问题，我们也应该定义一个二维的dp表

新的状态定义：

dp[i] [0]表示；第i天结束之后，处于买入状态可获得的最大利润

dp[i] [1]表示：第i天结束之后，处于可交易状态可获得的最大利润

dp[i] [2]表示：第i天结束之后，处于冷冻状态可获得的最大利润

3.状态转移方程

对于多状态问题而言，我们首先要画出状态转移图

状态转移图的几个核心要点：

本状态能不能到本状态
本状态能到什么状态，发生什么变化
什么状态能到本状态

本题的状态图如下：

由此可得状态转移方程：

有了状态转移图，状态转移方程就能很轻松的写出来了

4.初始化

首先进入的必定是买入状态，因此只需要初始化dp[0] [0]即可

dp[0] [0] = -prices[0]

5.填表顺序

根据状态转移方程，我们可以很清晰的看到，i受i-1的影响，因从左往右进行填表

6.返回值

由于i走到最后一步时可能处于三种状态的其中一种，所以取所有状态里的最大值

7.代码实现

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> dp(n,vector<int>(3));
        dp[0][0] = -prices[0];
        for(int i=1;i<n;i++)
        {
            dp[i][0] = max(dp[i-1][0],dp[i-1][1]-prices[i]);
            dp[i][1] = max(dp[i-1][2],dp[i-1][1]);
            dp[i][2] = dp[i-1][0] + prices[i];
        }

        int ans = 0;
        for(int i=0;i<3;i++)
        {
            ans = max(ans,dp[n-1][i]);
        }

        return ans;
    }
};

三、买卖股票的最佳时机IV

1.题目解析

买入并卖出视为一次交易，k次交易内可获得的最大利润

2.状态定义

根据经验+题目要求，dp[i]可以表示为：i天之后，可获得的最大利润

同时，也基于前面几题的分析，显而易见这是不可行的，i天可以处于两种状态，买入或卖出，也可能是第t次交易

因此，我们因对买入和卖出定义两个二维dp表

新的状态定义：

f[i] [j]：i天结束之后，完成了j次交易，，处于买入状态，所获得的最大利润

g[i] [j]：i天结束之后，完成了j次交易，，处于卖出状态，所获得的最大利润

3.状态转移方程

本题只有两种状态，状态转移图如下：

由此图可得状态转移方程：

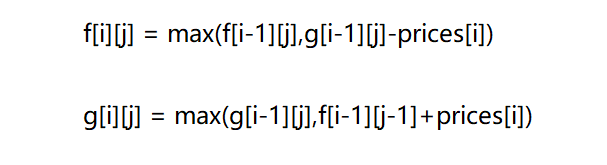
4.初始化

同样，首先进入的必定是买入状态

f[0] [0] = -prices[0]

填表从i=1开始，因此g[0] [0] 也得初始化

g[0] [0] = 0

5.填表顺序

i受i-1的影响，因此从左到右进行填表

交易次数是逐步增加的，因此从上到下填表

6.返回值

k次交易内的最大利润，f表并没有完成一次完整的交易，所以肯定不可能出现最大利润

只需对g表进行k次遍历，找出最大值即可

7.代码实现

有2个细节问题：

k次交易可能完全达不到：

天数为20天，交易次数k为30次，对于20天，最多只能进行10次交易，一定不可能出现30次交易的情况

因此我们可以对k进行优化，来省略一定的时间和空间

基于前面的经验，我们很可能会将dp表初始化为INT_MAX或INT_MIN,但这样一旦执行加法或者减法，会发生值越界的问题，因此我们一般初始化为0x3f3f3f3f

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        const int INF = 0x3f3f3f3f;
        int n = prices.size();
        k = min(n/2,k);
        vector<vector<int>> f(n,vector<int>(k+1,-INF));
        auto g = f;
        f[0][0] = -prices[0];
        g[0][0] = 0;
        
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<=k;j++)
            {
                f[i][j] = max(f[i-1][j],g[i-1][j]-prices[i]);
                g[i][j] = g[i-1][j];
                if(j>=1)
                    g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);
            }
        }

        int res = 0;
        for(int i=0;i<=k;i++)
            res = max(res,g[n-1][i]);
        return res;
    }
};