检查是否存在满足条件的数字组合
题目描述
给定一个正整数数组,检查数组中是否存在满足规则的数字组合
规则:A = B + 2C
输入描述
第一行输出数组的元素个数。
接下来一行输出所有数组元素,用空格隔开。
输出描述
如果存在满足要求的数,在同一行里依次输出规则里A/B/C的取值,用空格隔开。
如果不存在,输出0。
备注
- 数组长度在3-100之间。
- 数组成员为0-65535,数组成员可以重复,但每个成员只能在结果算式中使用一次。如:数组成员为[0, 0, 1, 5],0出现2次是允许的,但结果0 = 0 + 2 * 0是不允许的,因为算式中使用了3个0。
- 用例保证每组数字里最多只有一组符合要求的解。
用例
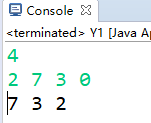
| 输入 | 4 |
| 输出 | 7 3 2 |
| 说明 | 7 = 3 + 2 * 2 |
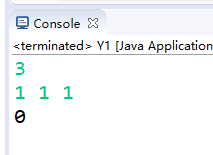
| 输入 | 3 1 1 1 |
| 输出 | 0 |
| 说明 | 找不到满足条件的组合 |
题目解析
-
需要明确的是每个数字出现的次数不大于数组中出现的次数,也就意味着每个索引只能使用一次。A=B+2C 这个A、B、C其实是可以重复的 如数组[0,0,0,1]中 是允许出现ABC分别为0,且满足条件的。
-
使用三重for循环 强行破解
-
使用数位规划算法来解题
for循环强行破解
import java.util.Scanner;
public class Y1 {
static int rawNums[]=null;
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int num=Integer.parseInt(sc.nextLine());
rawNums=new int[num];
for(int i=0;i<num;i++) {
rawNums[i]=sc.nextInt();
}
for(int i=0;i<num;i++) {
for(int j=0;j<num;j++) {
for(int k=0;k<num;k++) {
if(i==j||i==k||k==j)continue;
if(rawNums[i]==rawNums[j]+2*rawNums[k]) {
System.out.println(rawNums[i]+" "+rawNums[j]+" "+rawNums[k]);
System.exit(0);
}
if(rawNums[i]==rawNums[k]+2*rawNums[j]) {
System.out.println(rawNums[i]+" "+rawNums[k]+" "+rawNums[j]);
System.exit(0);
}
}
}
}
System.out.println(0);
}
}
数位DP算法进行求解
import java.util.Scanner;
public class Y1 {
static int rawNums[] = null;
static int tempNum[] = new int[3];// 存储取出的ABC
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int num = Integer.parseInt(sc.nextLine());
rawNums = new int[num];
for (int i = 0; i < num; i++) {
rawNums[i] = sc.nextInt();
}
dp(0, -1, -1);
System.out.println(0);
}
/**
*
* @param p 取到哪一层
* @param first 第一层取了哪个索引
* @param sencond 第二层取了哪个索引
*/
public static void dp(int p, int first, int sencond) {
if (p == 3) {
if (tempNum[0] == tempNum[1] + tempNum[2] * 2) {
System.out.println(tempNum[0] + " " + tempNum[1] + " " + tempNum[2]);
System.exit(0);
}
return;
}
for (int i = 0; i < rawNums.length; i++) {
if (i != first && i != sencond) {
tempNum[p] = rawNums[i];
if (p == 0) {
dp(p + 1, i, sencond);
}
if (p == 1) {
dp(p + 1, first, i);
}
if (p == 2) {
dp(p + 1, first, sencond);
}
}
}
}
}
代码运行示意图