目录
前言:
二叉树:
二叉树的种类:
二叉树的存储方式:
1. 链式存储
2. 数组存储
二叉树的遍历方式
深度优先遍历
广度优先遍历
总结:
前言:
本文将会详细的介绍各种常见的树以及相对应的概念,存储方式,遍历方式。树是经典的数据结构,因此我们虽然不能做到手撕各种树结构,但也要做到心中有B树。
二叉树:
二叉树是一种非常重要的树形结构,是一种特殊的树形结构,它的每个节点最多只有两个子节点。通常把这些子节点称作其左子节点和右子节点。
二叉树有许多应用,例如在搜索算法中经常用到。由于它具有以下几个重要的性质,因此在计算机科学中得到广泛应用:
- 每个节点最多只有两个子节点;
- 左子节点的键值总是小于其父节点的键值;
- 右子节点的键值总是大于其父节点的键值;
- 树中没有两个节点拥有完全相同的键值。
二叉树的种类:
二叉树是一种树形结构,其中每个节点最多只有两个子节点。除此之外,二叉树还可以分为多种不同的类型。
1. 普通二叉树: 普通二叉树(Binary Tree)没有什么特别的限制,只需每个节点最多有两个子节点即可。
2. 满二叉树: 满二叉树(Full Binary Tree)是一种特殊的二叉树,在满二叉树中,每个节点要么没有子节点(即为叶子节点),要么有两个子节点。满二叉树的层数为 h 时,它的节点数是 2^h-1。
3. 完全二叉树: 完全二叉树(Complete Binary Tree)是一种特殊的二叉树,除了最后一层,其他每一层的节点数都达到最大值。最后一层的节点必须全部靠左对齐。在完全二叉树中,可以将每个节点的编号进行按层编号,如果一个节点的编号为 i,则它的左子节点的编号为 2i,它的右子节点的编号为 2i+1。
4. 平衡二叉树: 平衡二叉树(Balanced Binary Tree)是一种特殊的二叉树,在这种树中,每个节点的左右子树的高度差不能超过 1。这种树可以保证在最坏情况下,树的高度不超过 O(log n),因此查找、插入、删除等操作的时间复杂度表现非常好,为 O(log n)级别。
5. 二叉搜索树: 二叉搜索树(Binary Search Tree, BST)是一种特殊的二叉树,对于任何一个节点,它的左子树中所有节点的键值都小于它的键值,右子树中所有节点的键值都大于它的键值。这样,我们就可以用二叉搜索树进行快速查找、插入和删除等操作。如果二叉搜索树的节点按照中序遍历的顺序输出,那么就是一个升序序列。
在二叉搜索树中,对于每个节点,它的左子树中所有节点的键值都小于它的键值,右子树中所有节点的键值都大于它的键值。因此,二叉搜索树中的元素是可以被快速地查找、插入和删除的。
重点介绍一下红黑树:
红黑树(Red-Black Tree)是一种自平衡的二叉查找树,它是由一些颜色为红色或者黑色的节点组成的。通过一些约束条件,红黑树保证了在最坏情况下也能进行快速的查找、插入和删除等操作。
红黑树的约束条件包含以下四点:
- 1. 每个节点为红色或黑色;
- 2. 根节点是黑色的;
- 3. 每个叶子节点(NIL节点,即空节点)都是黑色的;
- 4. 如果一个节点为红色,则它的两个子节点必须都是黑色的。
在这些约束条件下,红黑树拥有以下性质:
- 1. 从根节点到叶子节点的所有路径上,黑色节点的数量必须相等;
- 2. 任何一个节点的两个子树的高度差不能超过1。
通过这些约束条件和性质,红黑树将最坏情况下的复杂度从O(n)降低到O(log n)。因此,在实际应用中,红黑树往往用于需要快速查找、插入和删除等操作的场景,例如编译器、数据库等数据结构。
自平衡是指当我们对一棵树进行插入或删除节点等操作时,根据某些特定的方法重新构造树的形状,让树的高度在某些比较严格的限制下保持最小,从而使得树的查询等操作的效率保持在一个较高的水平。
二叉树的存储方式:
1. 链式存储
链式存储是二叉树最常用的存储方式。在链式存储中,每个节点由三个部分组成:数据域、左子节点指针和右子节点指针。每个节点都指向其左右子节点的指针为空或者指向相应节点。因此,每个节点可以用一个 C++ 结构体来表示:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
2. 数组存储
数组存储是二叉树的另一种存储方式。在数组存储中,我们可以使用数组来表示一棵二叉树,数组中每个元素就代表一个二叉树的节点。具体地,我们可以按照二叉树的层次遍历顺序,把二叉树的节点从上到下、从左到右排列在数组中。如果一个节点的下标为 i,那么它的左子节点下标为 2i+1,右子节点下标为 2i+2。叶子节点对应的数组元素为空。如果二叉树的层数为 h,这种存储方式需要使用 2^{h+1}-1 个元素。
数组存储的优点是可以节省指针开销并且由于数组的特性,我们可以利用下标来快速访问我们想要访问的节点,但是必须预先分配足够的空间,并且不能很好地支持动态插入和删除等操作。因此,在实际应用中,链式存储更为常用。
综上,二叉树的存储方式有链式存储和数组存储两种,链式存储是最常用的一种存储方式,而数组存储则更适合静态二叉树。
二叉树的遍历方式
-
深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
-
广度优先遍历
- 层次遍历(迭代法)
深度优先搜索(Depth-First Search, DFS)和广度优先搜索(Breadth-First Search, BFS)都是图搜索算法,用于在图中查找特定的节点或寻找一条路径。它们都属于盲目搜索算法,也就是不使用任何启发式信息来指导搜索。它们的主要区别在于搜索过程中节点的遍历顺序。
深度优先搜索从起点节点开始,每次尽可能沿着一条未被探索的分支一直搜索下去,直到到达最深处,然后回溯到前一个节点,继续搜索下一个分支。这个过程类似于树的深度优先遍历。
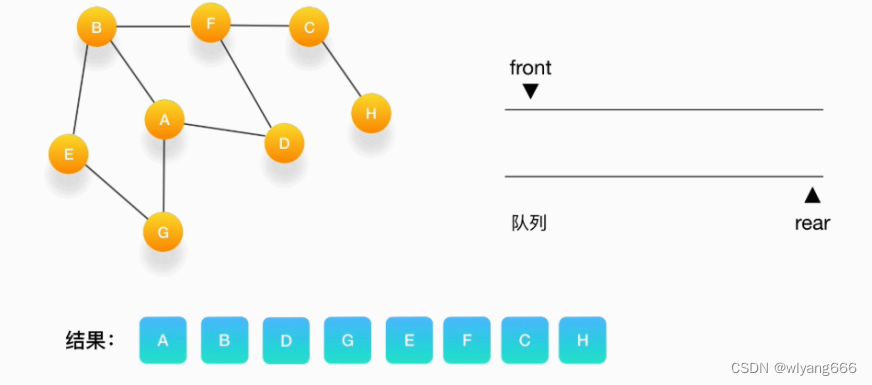
广度优先搜索从起点节点开始,每次先访问起点的所有邻居节点,然后访问所有邻居节点的邻居节点,然后再访问邻居节点的邻居节点的邻居节点,依次类推。这个过程结构类似于树的广度优先遍历。
一般来说,如果我们想要在连通的图中搜索到所有的节点,我们通常会采用广度优先搜索。而如果我们只是需要在树或图中搜索一个可能存在于远离根部的分支的目标节点,那么可以使用深度优先搜索来快速找到目标节点。深度优先搜索也可以被用于选择最优解的应用,例如AI博弈。
二叉树的遍历是一种递归算法,每个节点都会被访问到且仅被访问一次。二叉搜索树的查找、插入和删除操作也是基于递归算法实现的。
图解前中后序遍历:
前序遍历:遍历节点方式为中左右
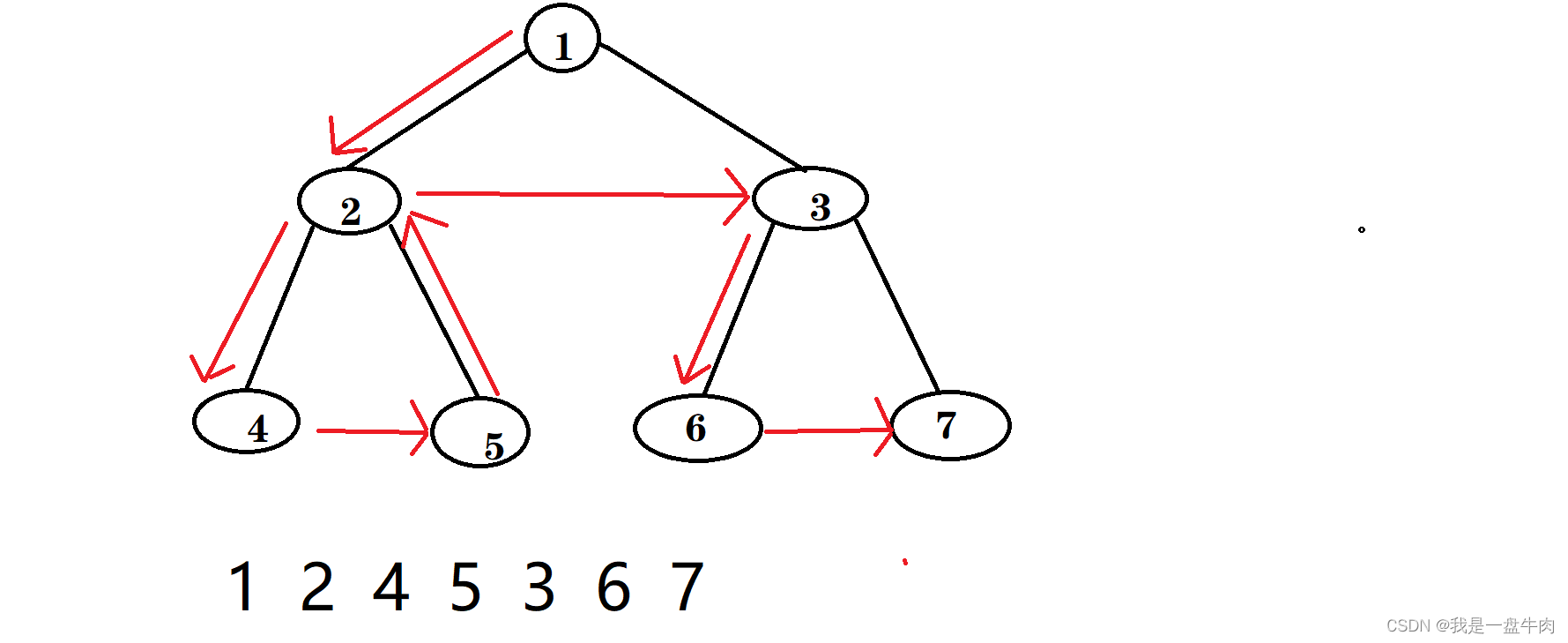
中序遍历:遍历节点方式为左中右
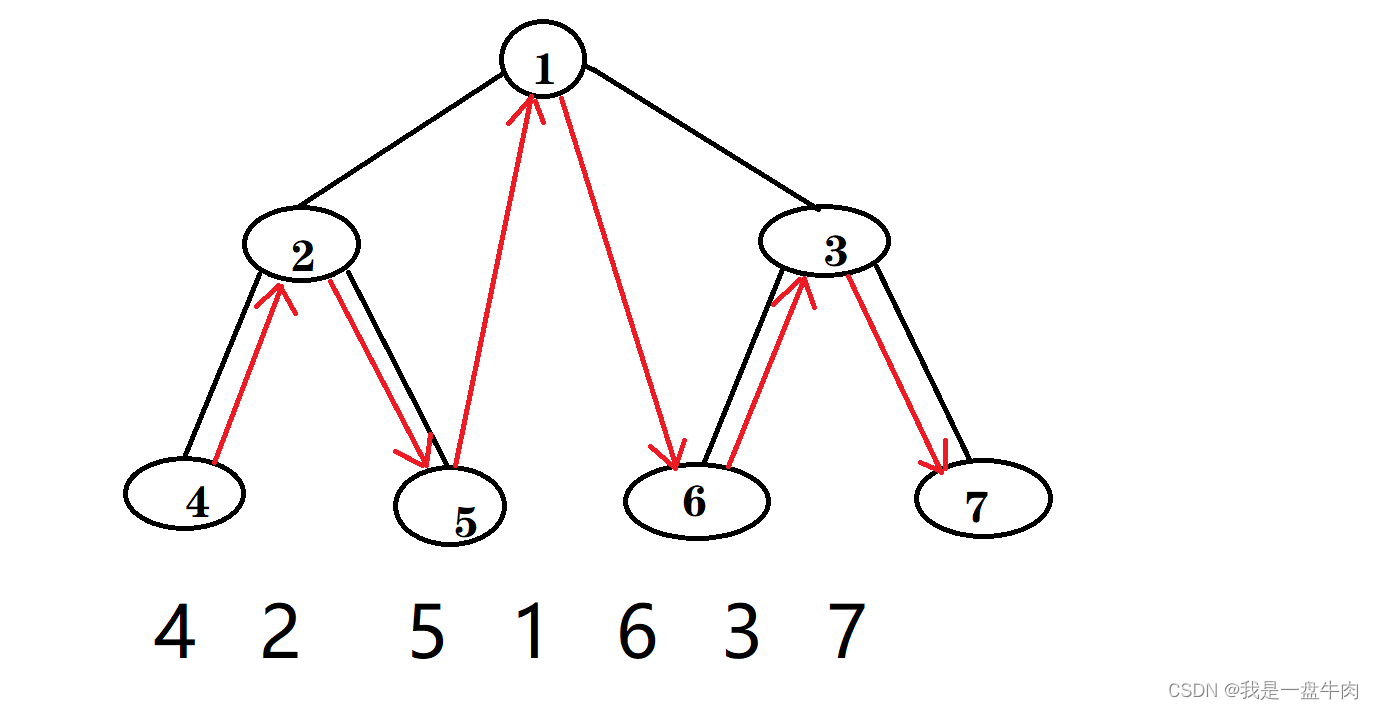
后序遍历:遍历节点方式为左右中
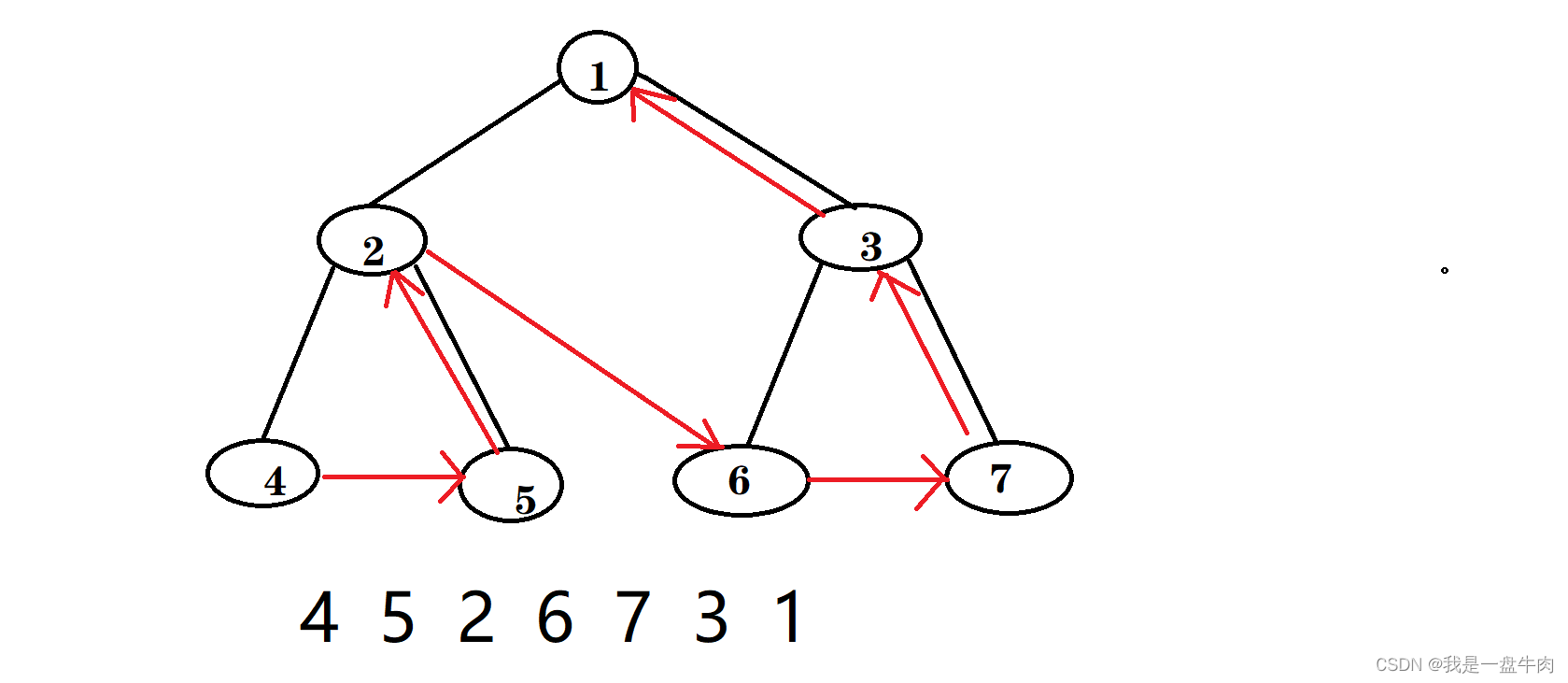
总结:
本篇我们对二叉树的各项基础概念做了介绍,下几篇我们将会针对几个比较常见的树,进行手撕解析,带领大家探寻树这种数据结构的奥妙。
如果我的内容对你有帮助,请点赞,评论,收藏。创作不易,大家的支持就是我坚持下去的动力!