16、买卖股票的最佳时机含手续费

(1) 题目分析

完成一笔交易才算达成交易。但其实你可以将手续费加在任意一处上。

(2) 算法原理

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();

        vector<int> f(n);
        auto g = f;

        f[0] = -prices[0];
        g[0] = 0;

        for(int i=1; i<n; ++i){
            f[i] = max(f[i-1],g[i-1] - prices[i]);
            g[i] = max(g[i-1],f[i-1] + prices[i] - fee);
        }

        return max(g[n-1],f[n-1]);
    }
};

17、买卖股票的最佳时机Ⅲ

(1) 题目解析

(2) 算法原理

注: 如果仅仅考虑填无穷的话，如果是一个有符号的整型，减去一个负数，会变成一个无比大的正数，会影响dp表的取值。因此我们这里定义一个 MIN_INT:0x3f3f3f 这是一个通常用来作为"最大值或最小值"的数，因为它不管怎么加减，都不会溢出，出现未定义行为。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        const int MIN_INT = -0x3f3f3f3f;

        vector<vector<int>> f(n,vector<int>(3,MIN_INT));
        auto g = f;
        // 初始化
        f[0][0] = -prices[0];
        g[0][0] = 0;

        for(int i=1; i<n; ++i)
        {
            for(int j=0; j<3; ++j)
            {    
                // 填表更新
                f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);
                g[i][j] = g[i-1][j];
                if(j >= 1)
                    g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);
            }
        }
        
        // 查询最大值
        int ret = 0;
        for(int i=0; i<3; ++i){
            ret = max(ret,g[n-1][i]);
        }
    
        return ret;
    }
};

18、买卖股票的最佳时机Ⅳ

(1) 题目解析

如果你对上面进行 "至多两笔交易" 特别熟悉，也弄懂了状态表达和状态方程式，那么这解这道题的代码，甚至可以说 "原封不动" copy一份即可。

(2) 算法原理

这里就省略省略，因为前面的一道题费了很多口舌。只是值得注意，虽然说的是至多k次交易，但是有k+1种情况。

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        const int MIN_INT = -0x3f3f3f3f;

        vector<vector<int>> f(n,vector<int>(k+1,MIN_INT));
        auto g=f;
        f[0][0] = -prices[0];
        g[0][0] = 0;

        for(int i=1; i<n; ++i){
            for(int j=0; j<=k; ++j){
                f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);
                g[i][j] = g[i-1][j];

                if(j>=1)
                    g[i][j] = max(g[i-1][j],f[i-1][j-1] + prices[i]);
            }
        }
        int ret = 0;
        for(int i=0; i<=k;++i){
            ret = max(ret,g[n-1][i]);
        }

        return ret;
    }
};

19、最大数组和

(1) 题目解析

(2) 算法原理

针对这种子序数组问题，一定要将问题划分为长度为1 或者长度>1,每个长度的子序数组都可能成为dp[i-1]的答案一种。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        
        vector<int> dp(n+1);
        
        int maxVal = INT_MIN;
        for(int i=1; i<=n; ++i){
            dp[i] = max(nums[i-1],dp[i-1]+nums[i-1]);
            maxVal = max(maxVal,dp[i]);
        }

        return maxVal;
    }
};

20、环形数组的最大和

(1) 题目解析

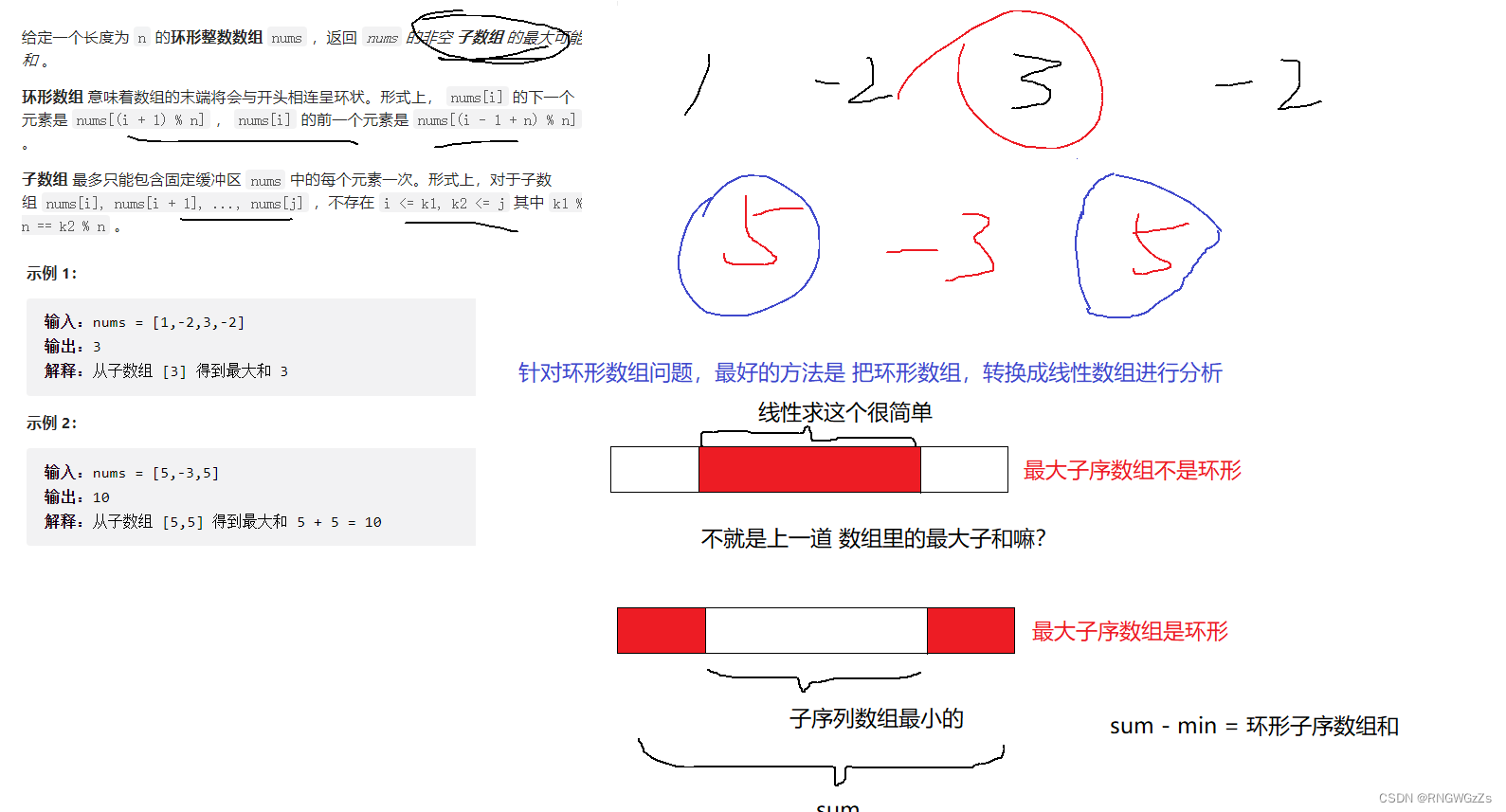
(2) 算法原理

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {
        int n = nums.size();

        vector<int> f(n+1);
        auto g = f;

        int sum = 0;
        int max_fn = INT_MIN;
        int min_gn = INT_MAX;
        for(int i=1; i<=n; ++i)
        {
            f[i] = max(nums[i-1],f[i-1]+nums[i-1]);
            max_fn = max(max_fn,f[i]);

            g[i] = min(nums[i-1],g[i-1]+nums[i-1]);
            min_gn = min(min_gn,g[i]);
            sum += nums[i-1];
        }

        int max_gn = sum - min_gn;
        // sum == min_gn?
        return max_gn == 0 ? max_fn : max(max_fn,max_gn);
    }
};

本篇到此结束，感谢你的阅读。

祝你好运，向阳而生~