一.最小生成树算法

1.概念（Minimum-Spanning-Tree）MST

生成树：针对于连通图，包含全部顶点，去掉一条边后不连通，加一条边形成环
最小生成树:带权连通无向图，边的权值之和最小的生成树(MST)

2.普里姆Prim算法（顶点）

从一个顶点开始出发，选择这个顶点代价最小的顶点进行构造，重复执行，一直到所有顶点全部进入生成树中
只关注顶点,，时间复杂度：O(|V|)
适合边稠密图

//伪代码核心
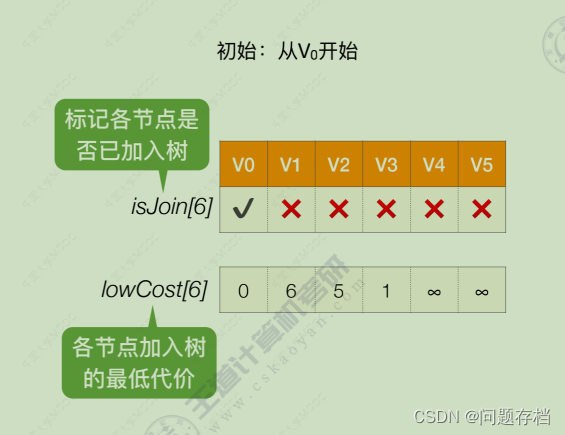
1.节点入树数组
isJoint[v];
2.用于更新各顶点的代价地图
lowCost[v];

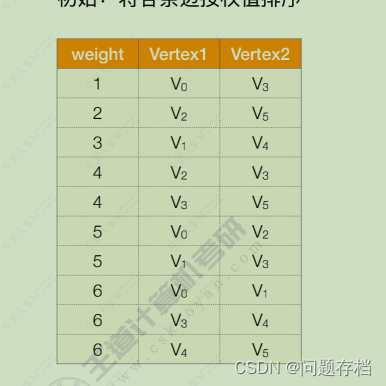
在这里插入图片描述

3.Kruskal最小生成树算法（边）

算法执行过程：
从代价最小的一条边出发，选择最小的两端顶点未连接的边，不断重复，直到把全部顶点装入生成树中
只关注边，时间复杂度O(|E|log2|E|)
适合边稀疏图
在这里插入图片描述

二、最短路径生成算法

1.BFS寻找无向不带权图最短路径

适用于无权无向图寻找最短路径

相关代码原理：

d[i]:表示从u到i结点的最短路径
path[i]:最短路径从哪个顶点过来**

bool visited[MAX_VERTEX_NUM]; //记录该节点是否访问过

    void BFS_MIN_Distance(Graph G, int u)
    {
        for (i = 0; i < G.vexnum; ++i)
        {
            d[i] = 无穷       //初始化路径长度
            path[i] = -1; //最短路径从哪个顶点过来
        }
        d[u] = 0;
        visited[u] = TRUE;
        EnQueue(Q, u);
        while (!= isEmpty(Q))
        {
            DeQueue(Q, u);
            for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor)
            {
                if (!visited[w])
                {
                    d[w] = d[u] + 1;
                    path[w] = u;
                    visited[w] = TRUE;
                    EnQueue(Q, w);
                }
            }
        }

2.Dijkstra寻找有向非负权图最短路径（单源最短路径）

不适合权值为负的有向图

三个用到的数组:

1、标记各节点是否已经找到最短路径
    final[vex.num];
2.记录各个点的路径长度 
dist[vex.num];
3.路径上的前驱
 path[vex.num];

方法体：

void Dijkstra(int u)
{
    // 1.dij初始化
    memset(vis, 0, sizeof(vis));
    for (int t = 1; t <= n; t++)
    {
        dis[t] = map[u][t]; //让dis对应某一点到另外各点的距离
    }
    vis[u] = 1; //设置该点访问过
    // 2.找到最小点
    for (int t = 1; t < n; t++)
    {
        int minn = Inf;
        int temp;
        for (int i = 1; i <= n; i++)
        {
            if (!vis[i] & dis[i] < minn)
            {
                minn = dis[i];
                temp = i;
            }
        }
        vis[temp] = 1; //让它被访问
        // 3.更新距离
        for (int i = 1; i <= n; i++)
        {
            if (map[temp][i] + dis[temp] < dis[i])
            {
                dis[i] = map[temp][i] + dis[temp];
            }
        }
    }
}