定积分是微积分中的一个重要概念，表示在给定区间上函数曲线下的面积或有向曲线与坐标轴围成的面积。定积分通常用符号 ∫ 来表示，具体形式为 ∫f(x) dx。

对于给定的函数 f(x) 和区间 [a, b]，定积分的计算可以通过求函数 f(x) 在该区间上的原函数 F(x) 的差值来实现，即计算 F(b) - F(a)。这里的 F(x) 称为 f(x) 的一个原函数。

如果函数 f(x) 在区间 [a, b] 上连续或者只有有限个间断点，并且存在一个原函数 F(x)，那么定积分 ∫[a, b] f(x) dx 就等于 F(b) - F(a)。

定积分的计算可以采用不同的方法，其中较为常见的方法包括基本积分公式、换元积分法和分部积分法等。

需要注意的是，定积分的结果不仅仅表示函数曲线下的面积，还可以表示函数曲线上方和下方的有向面积。

定积分

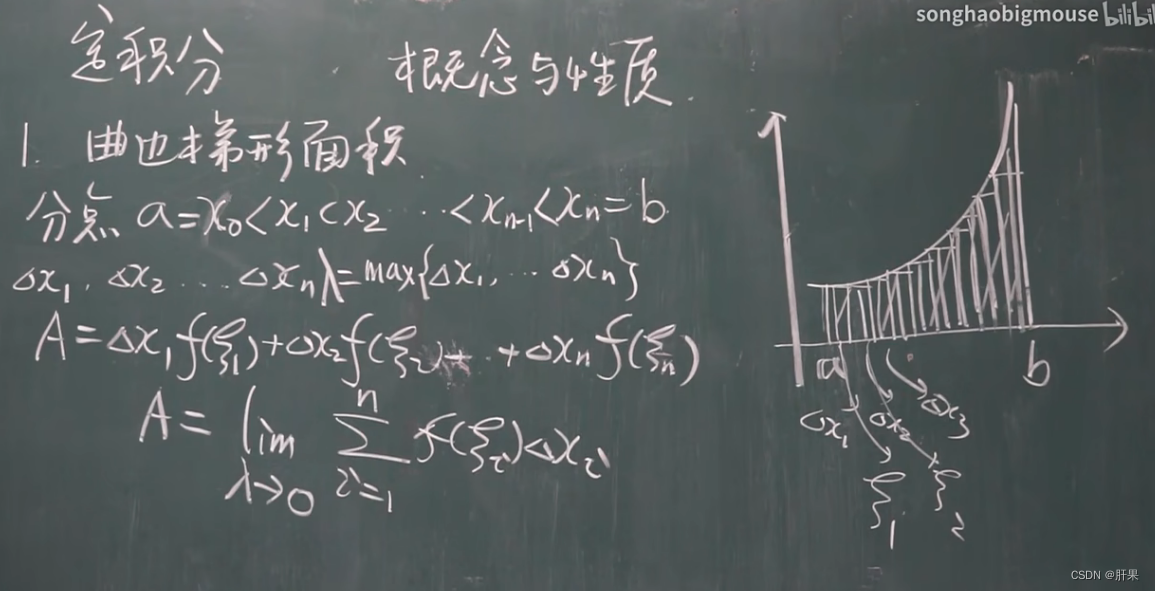
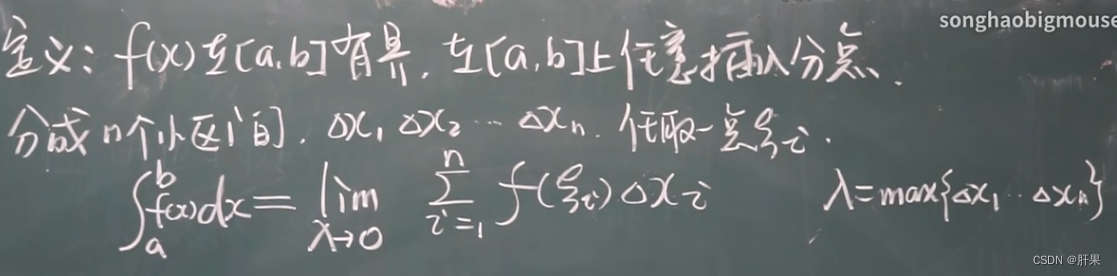
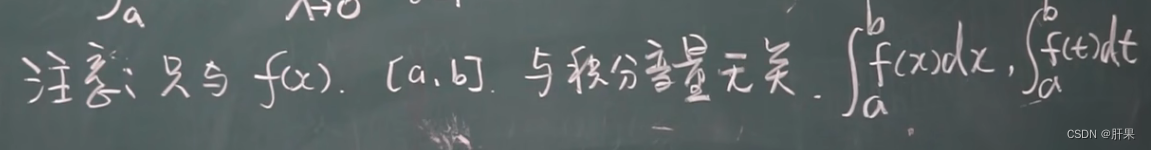
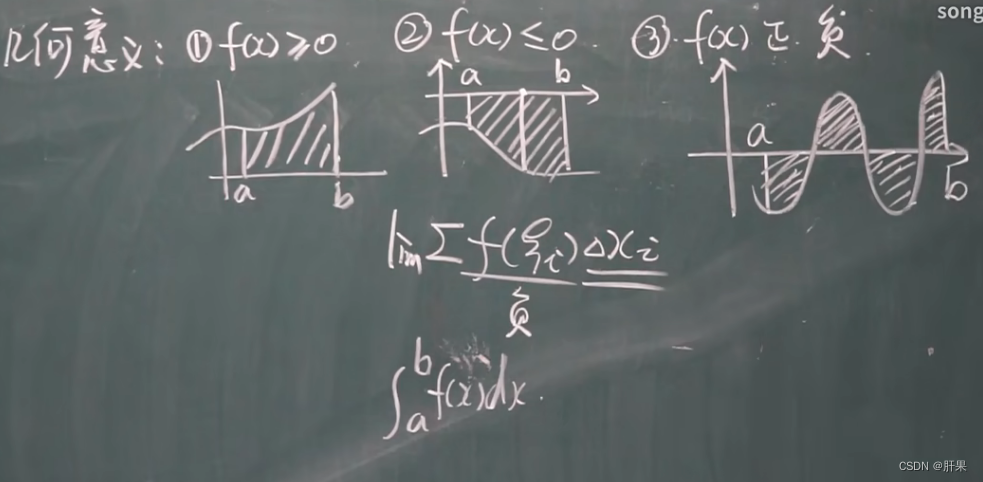
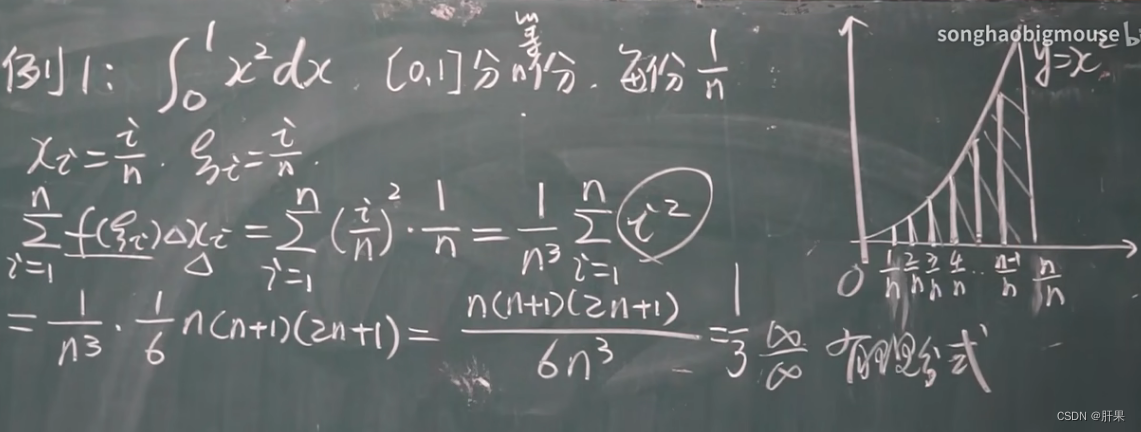
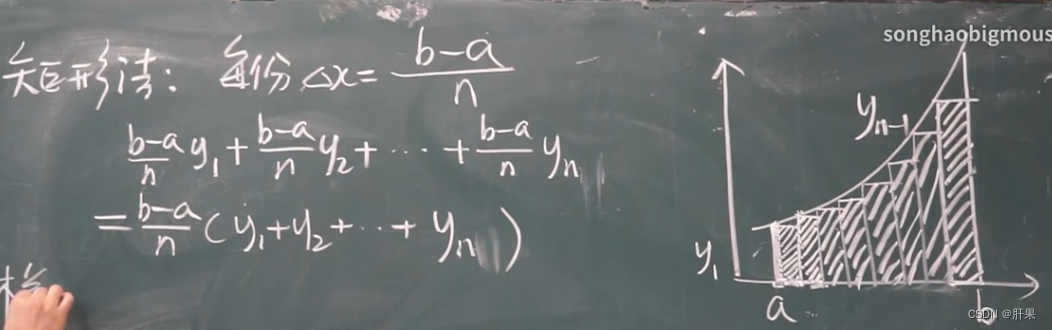
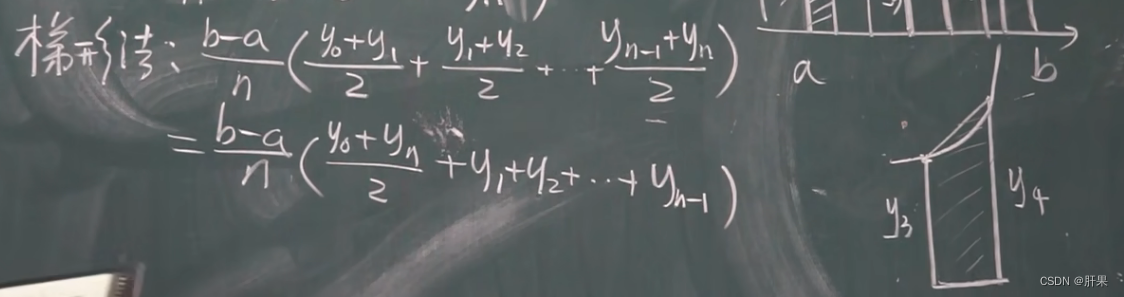
定积分性质

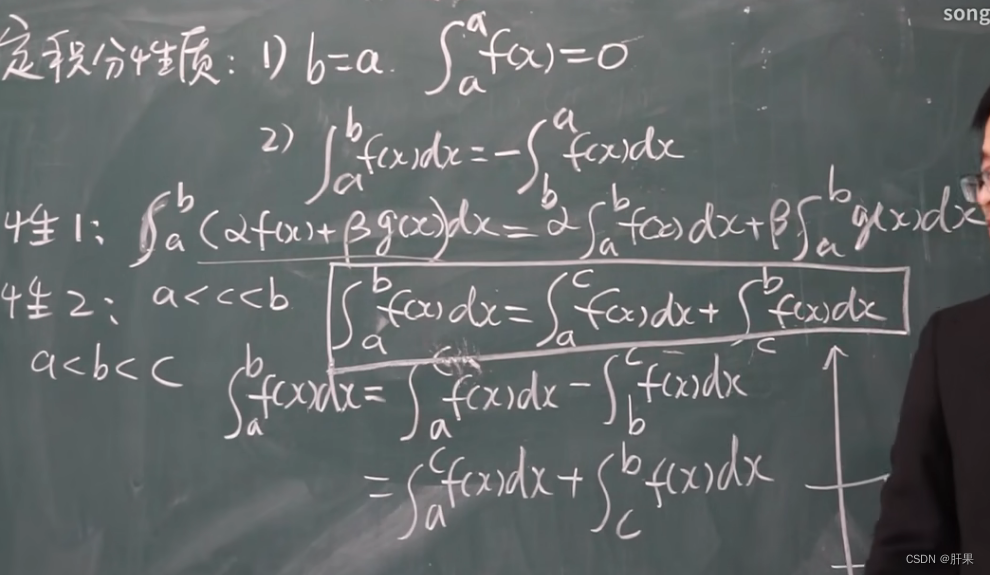
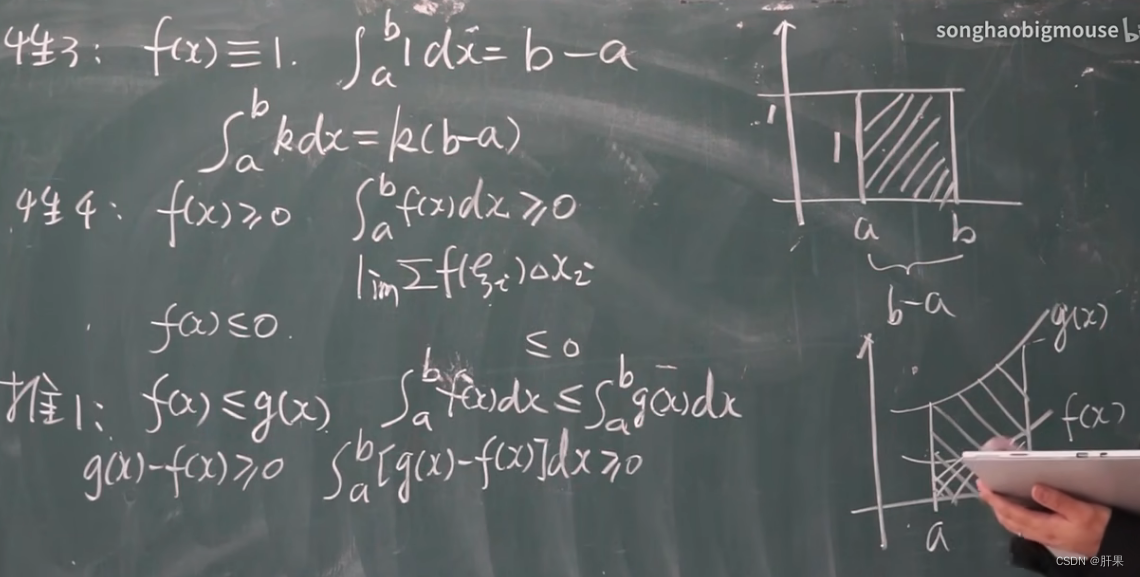
微积分基本公式

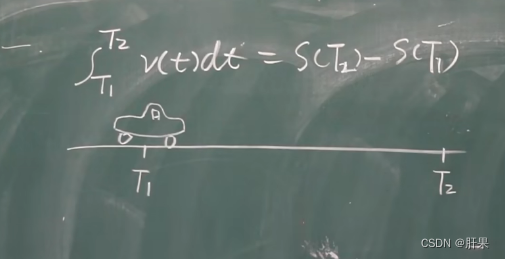
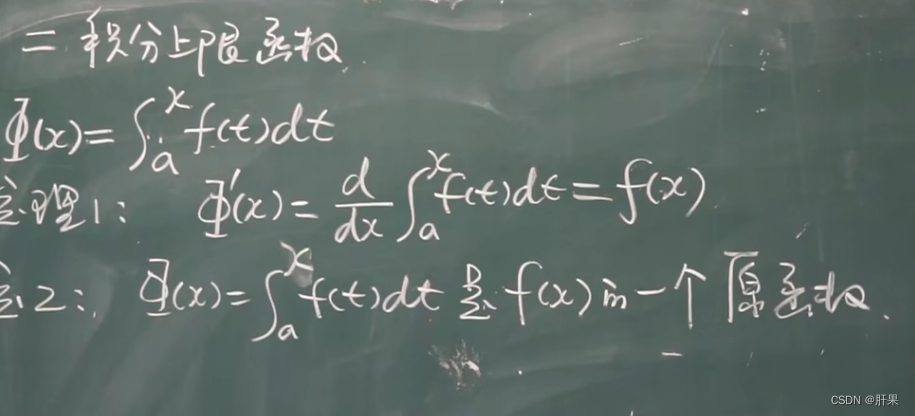
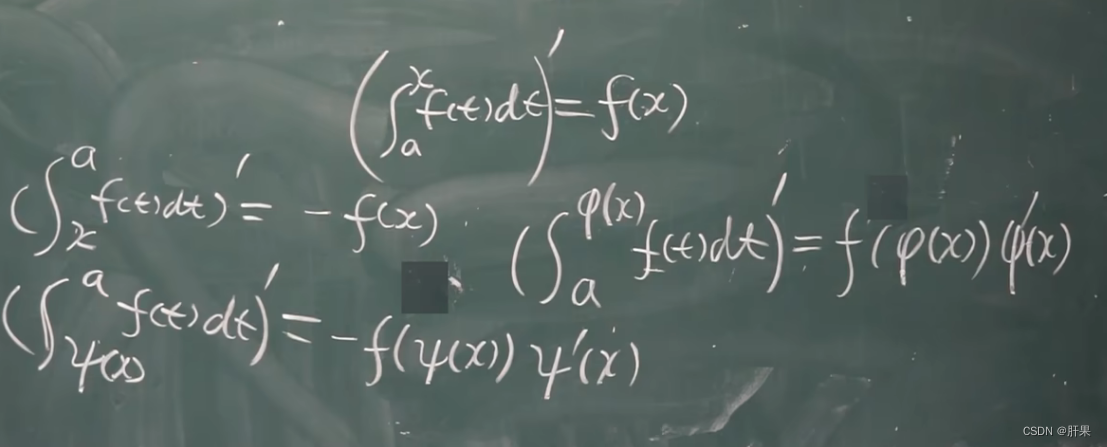
重点记这个公式：

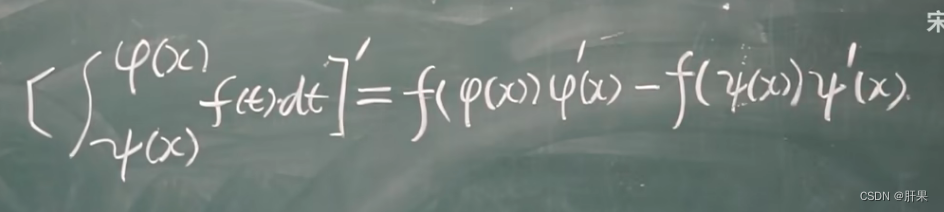
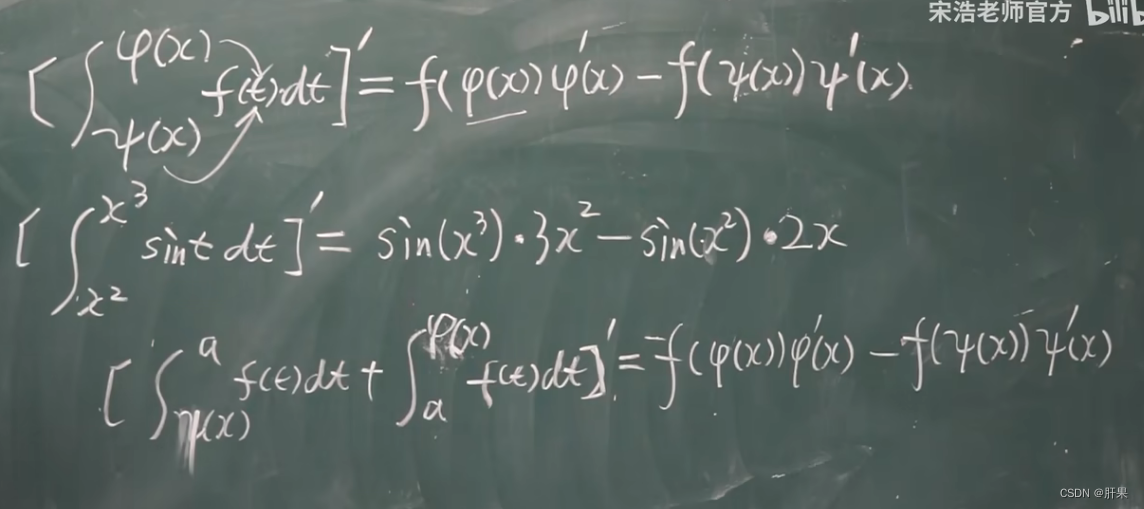
非常重要

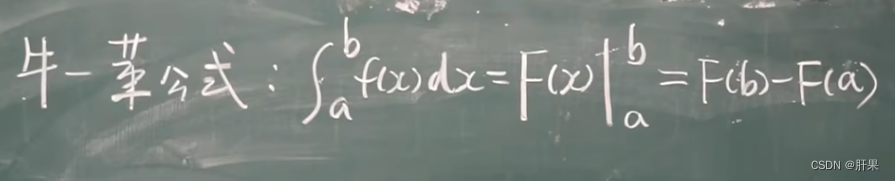
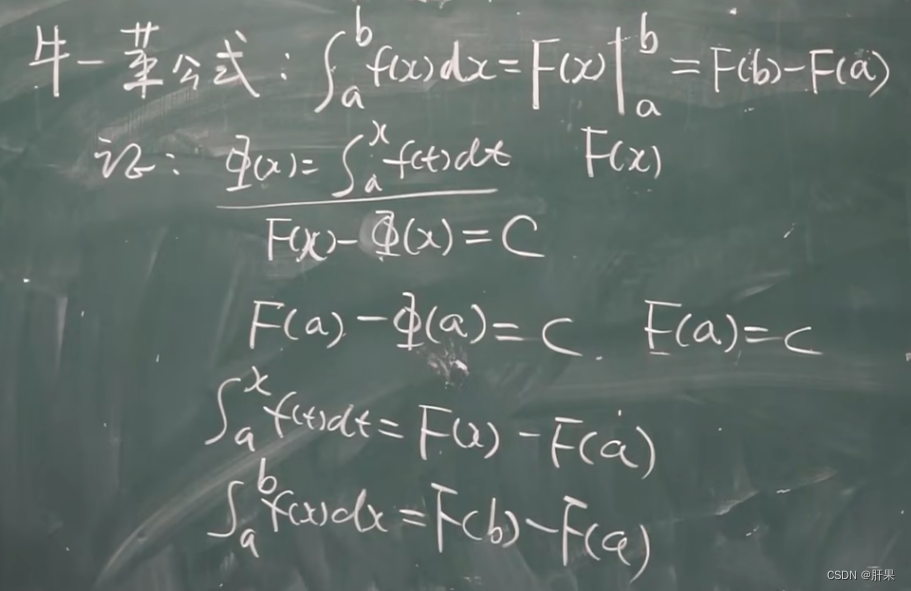
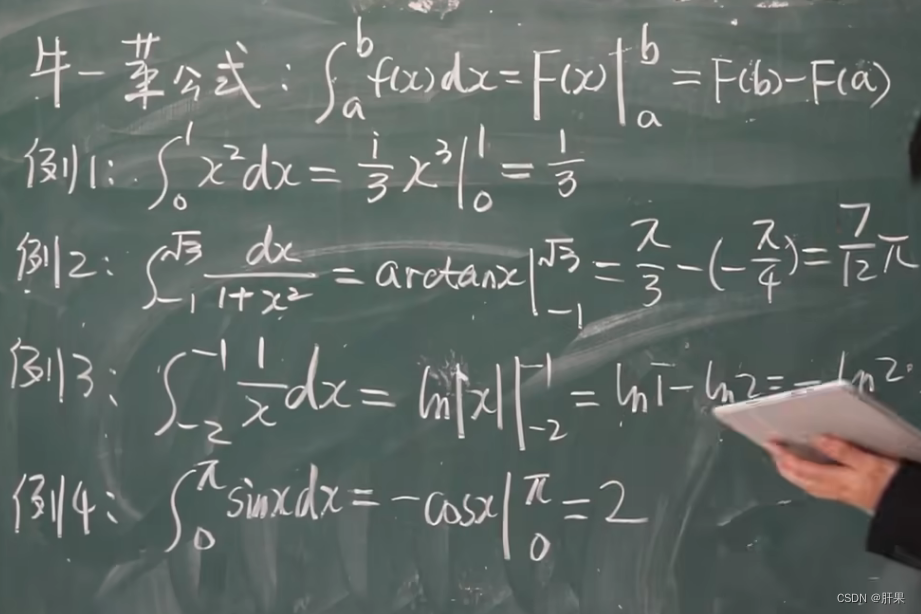
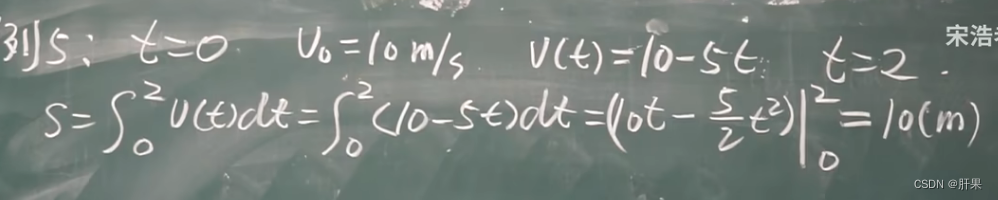
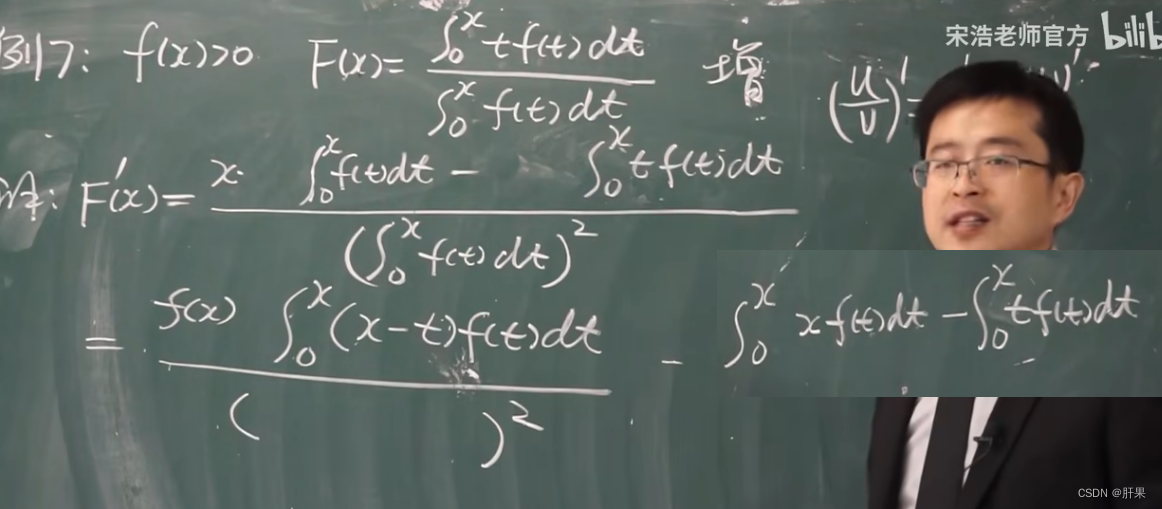
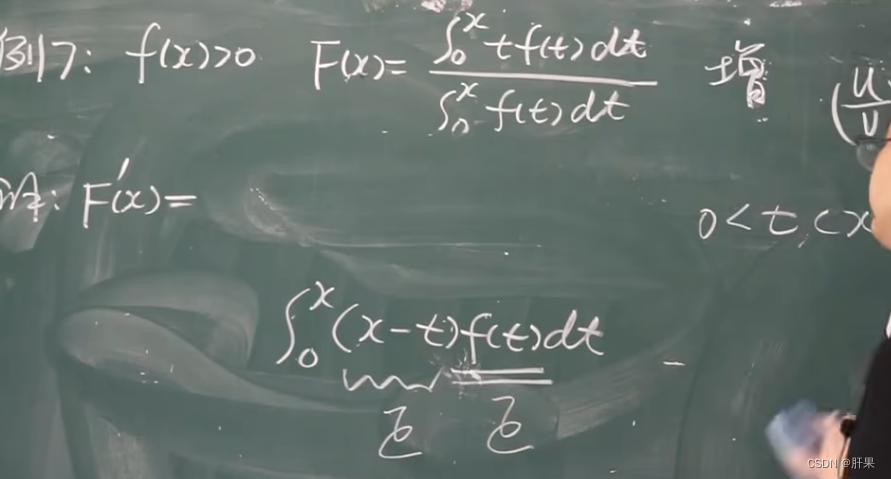
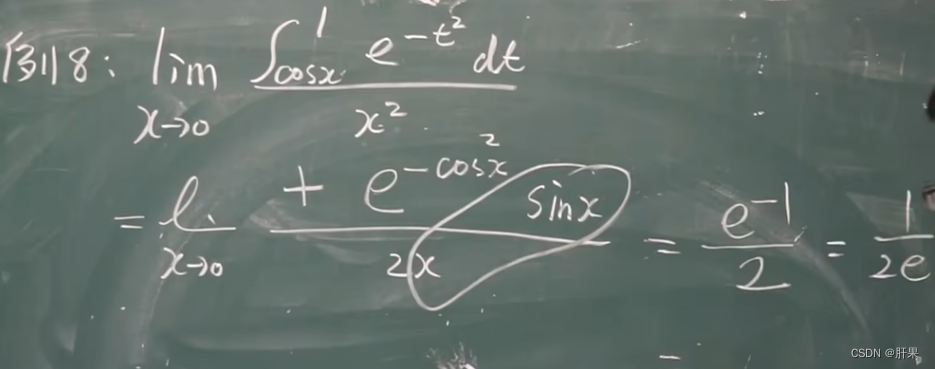
定积分的换元法

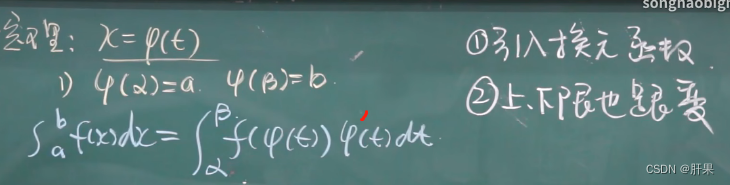
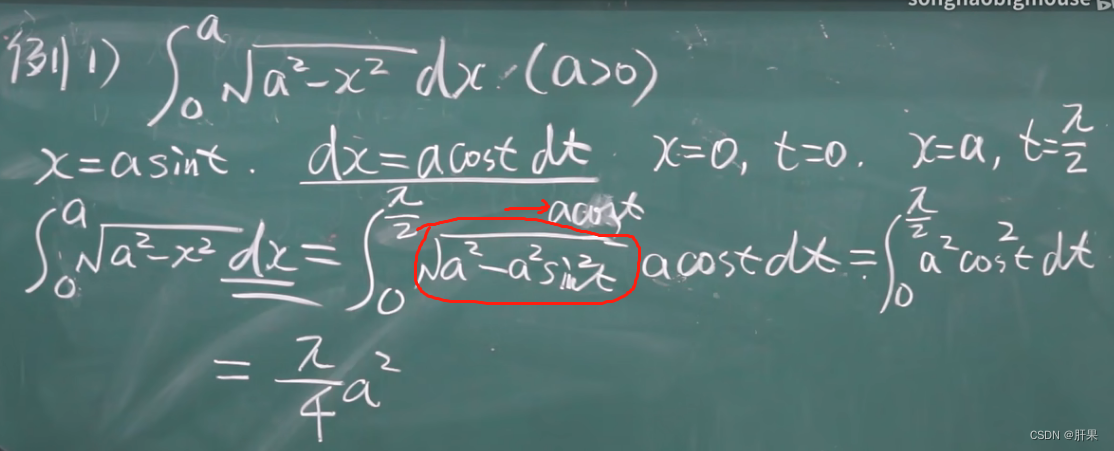
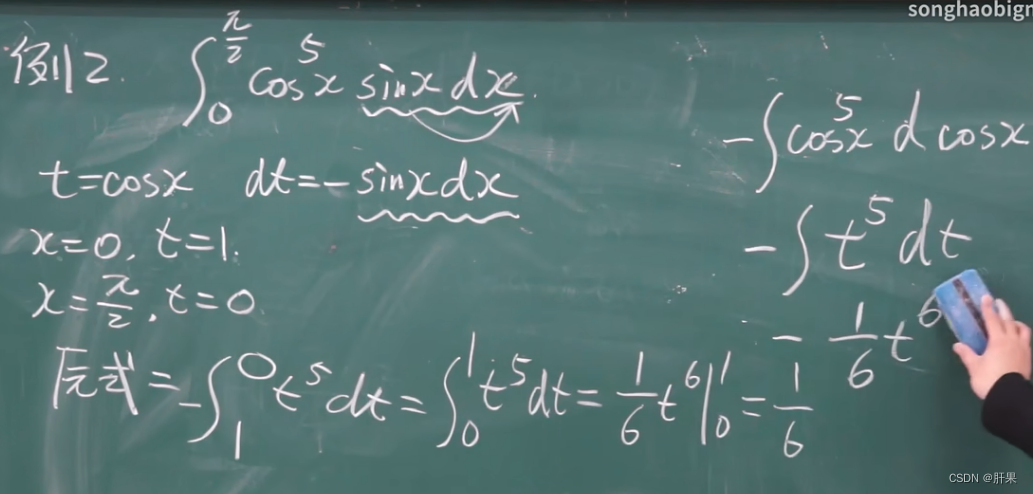
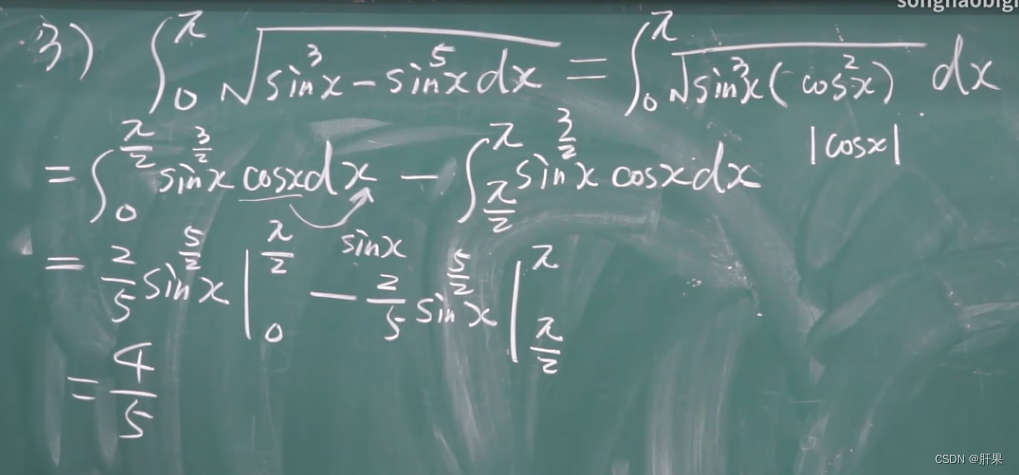
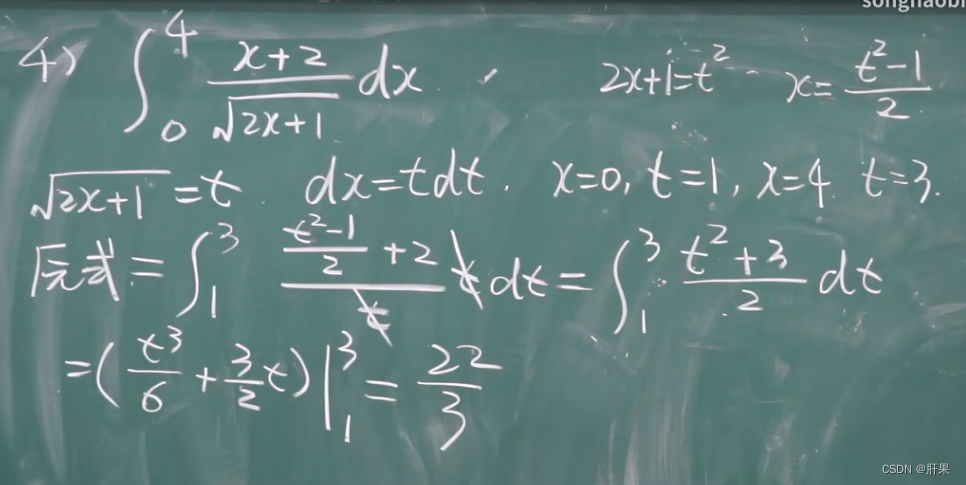
重点例题（结论考试必出）

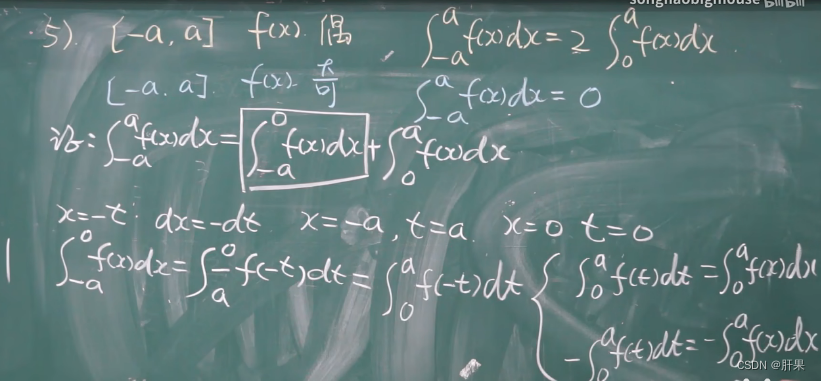
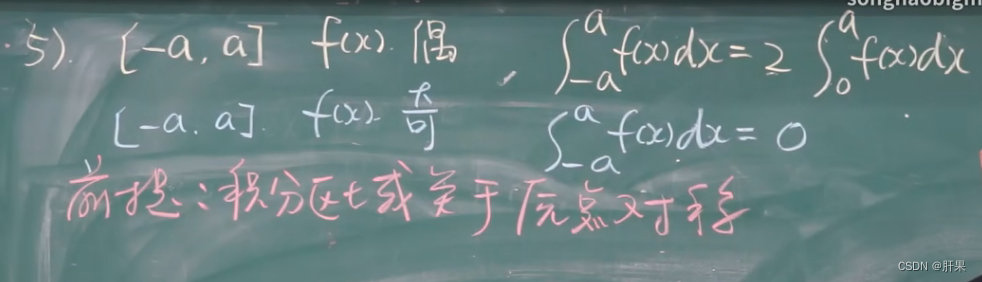
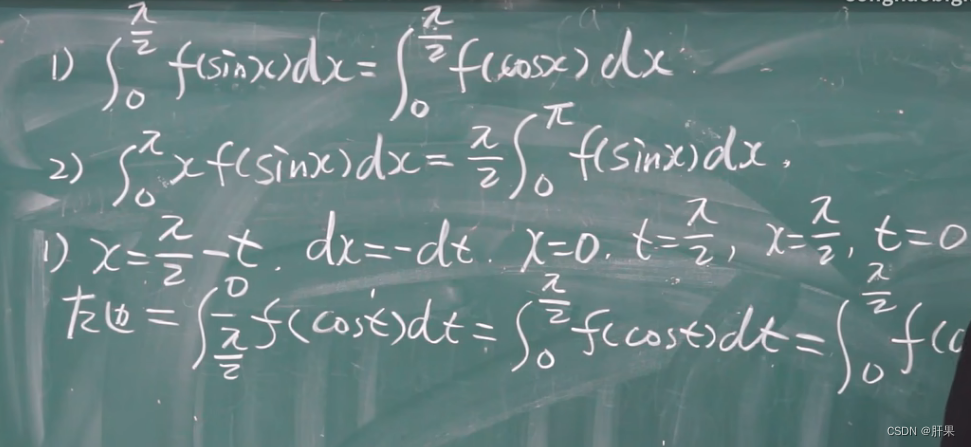
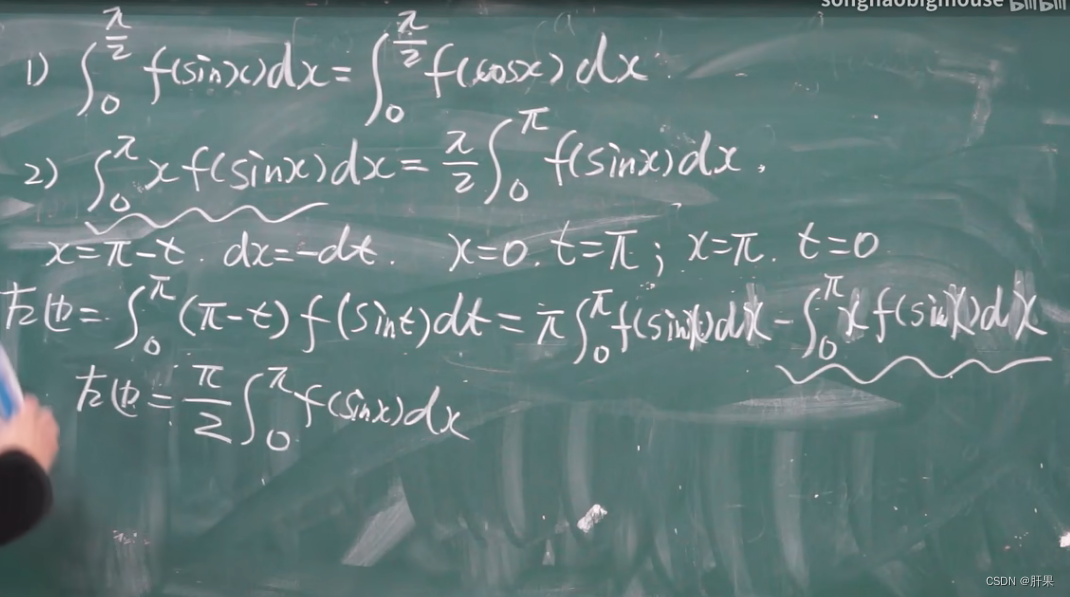
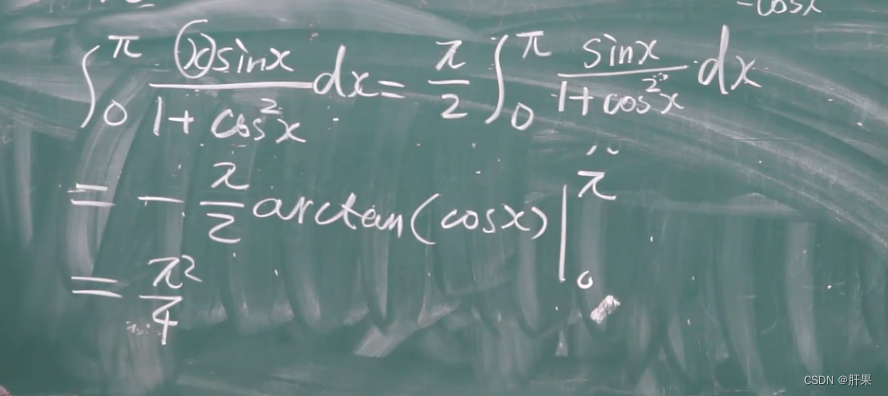
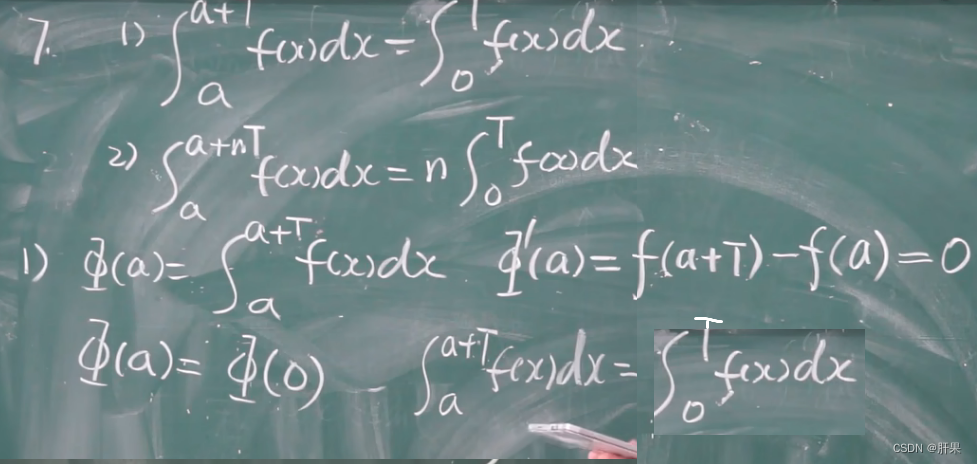
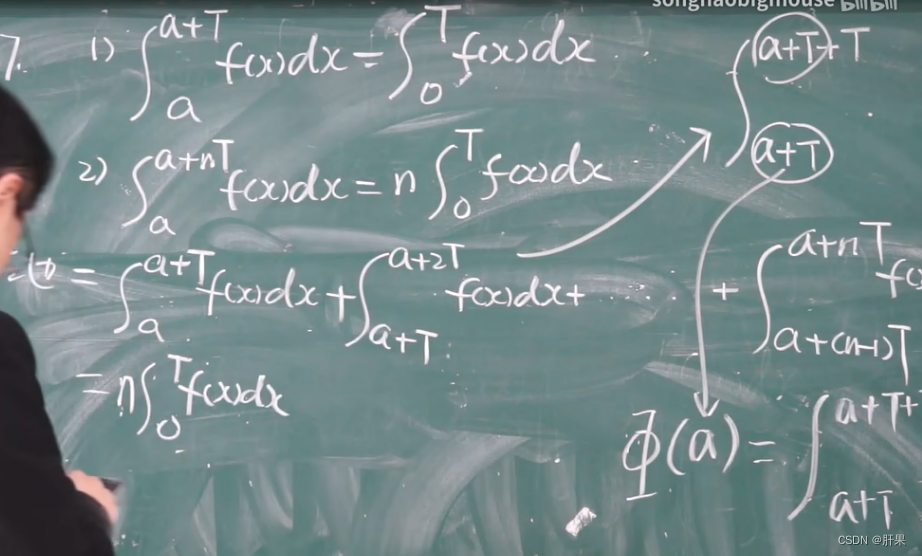
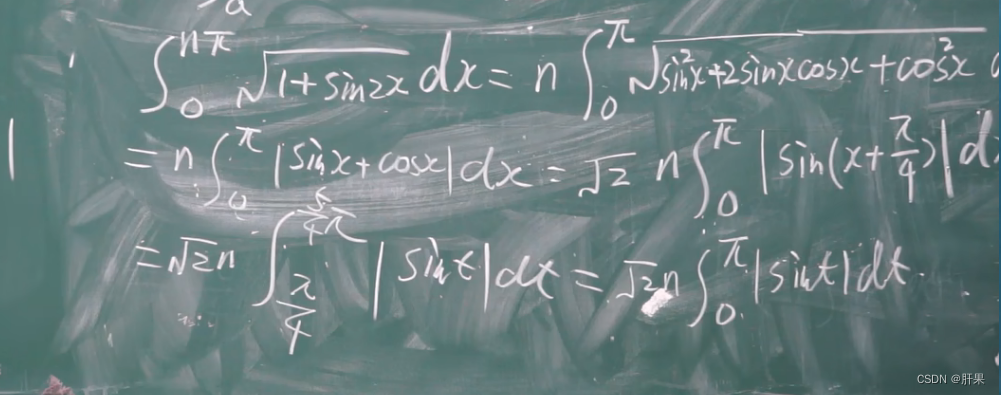
分部积分

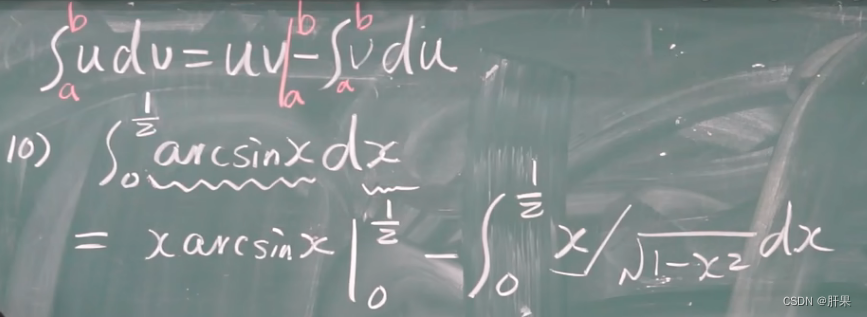
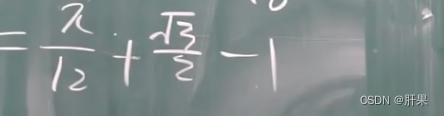
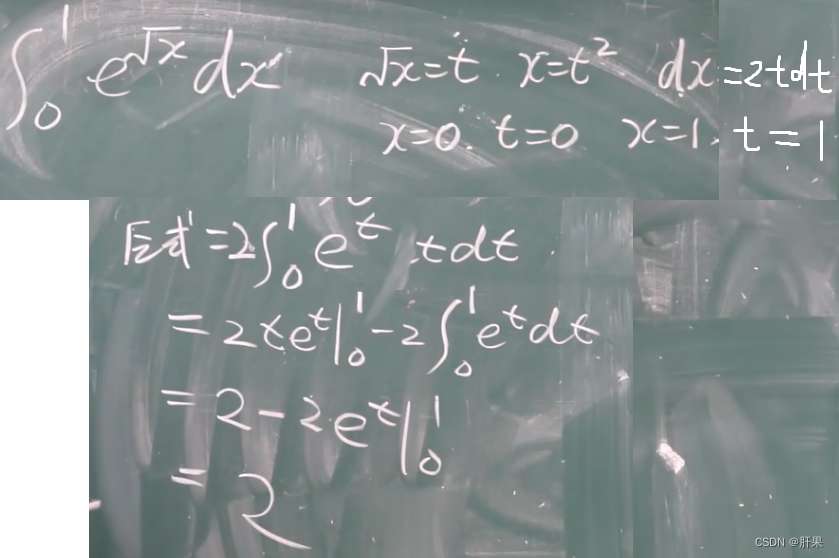
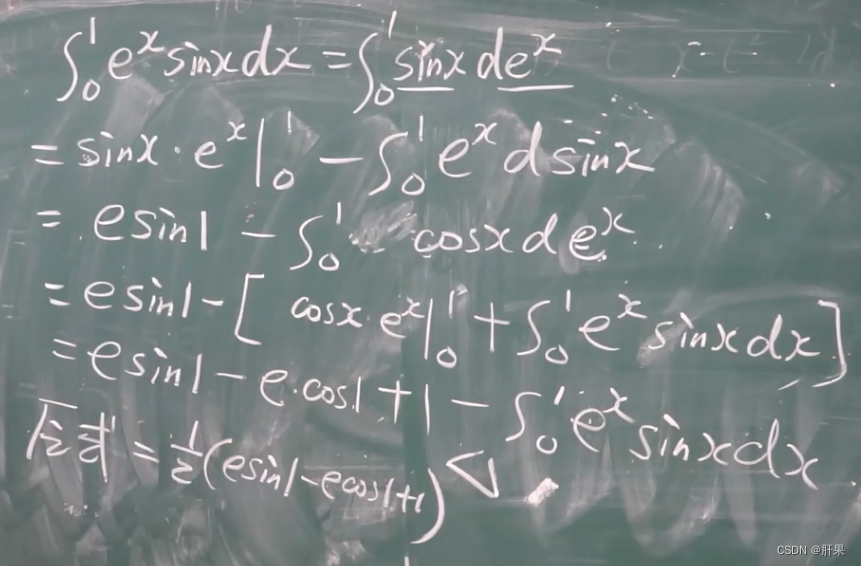
反常积分（广义积分）

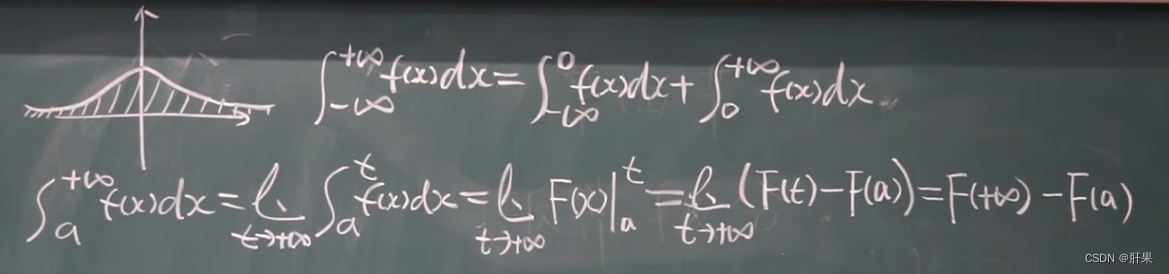
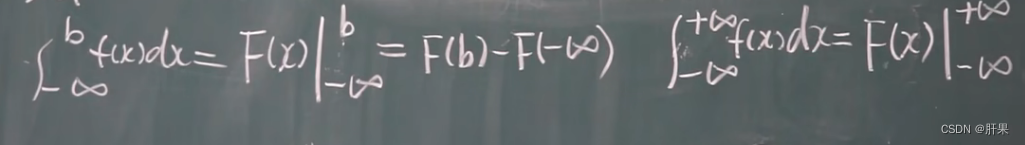
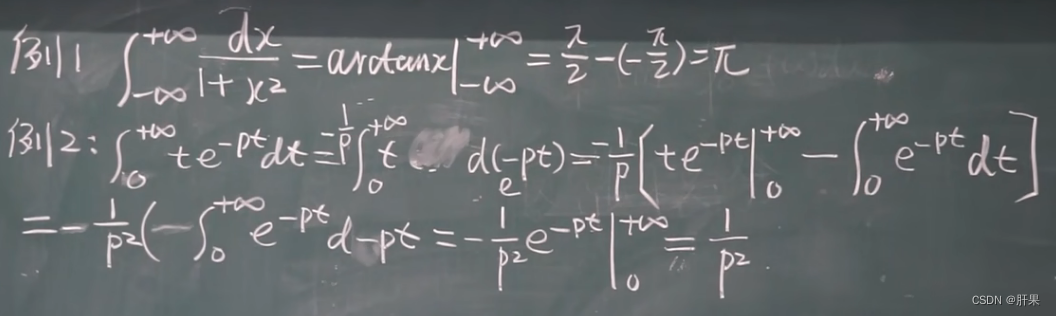
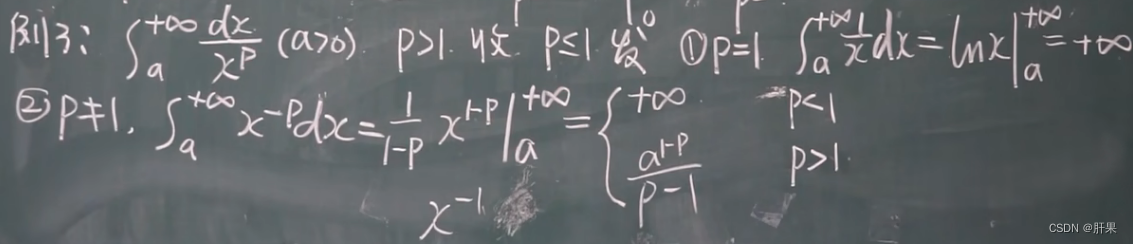
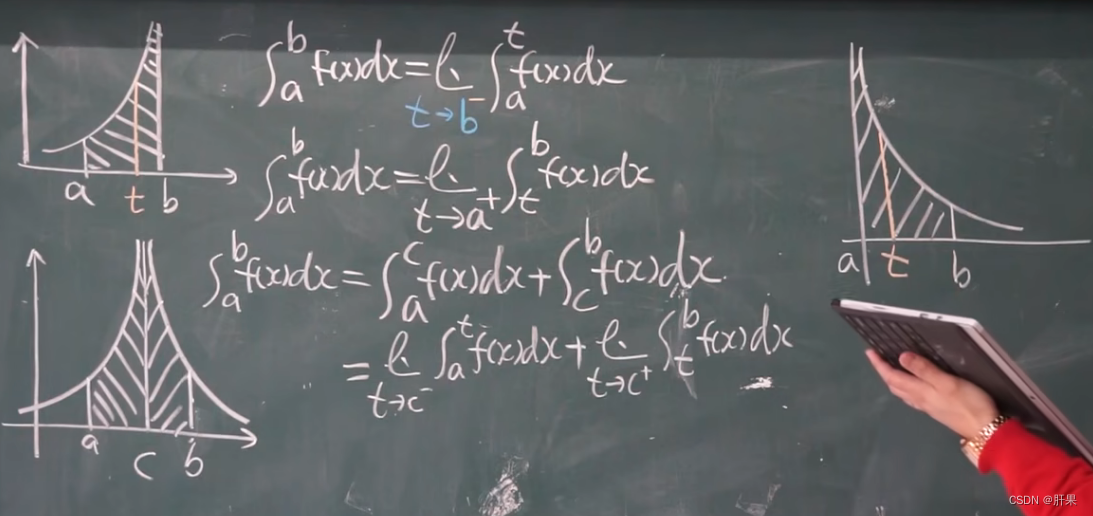
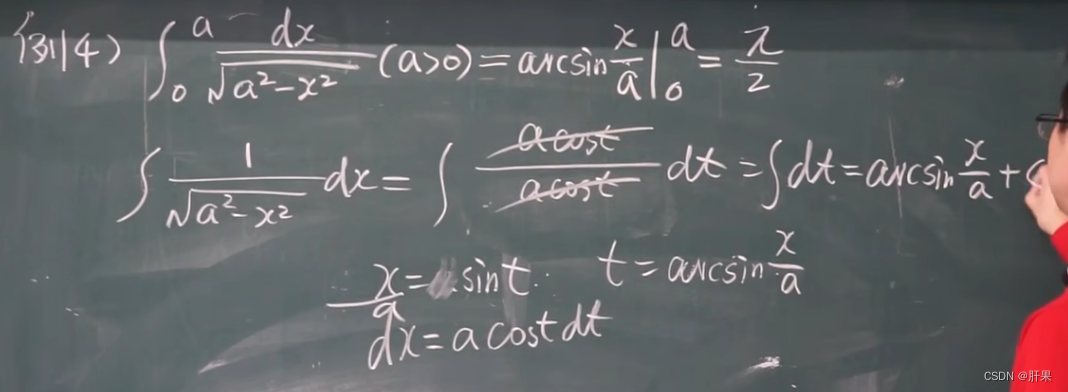
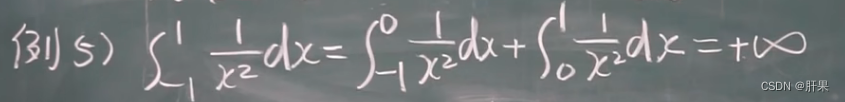
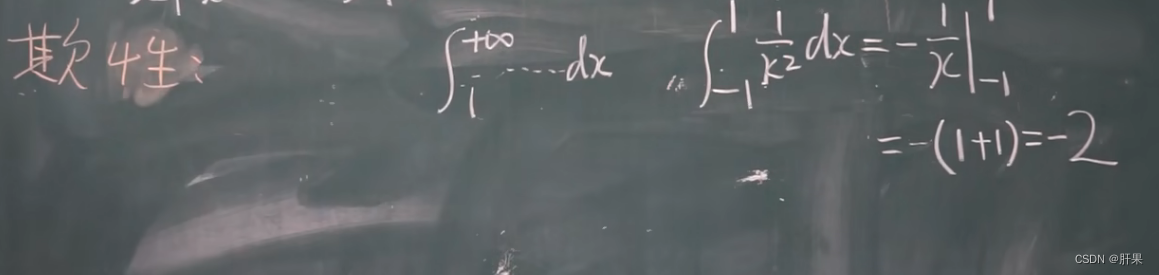
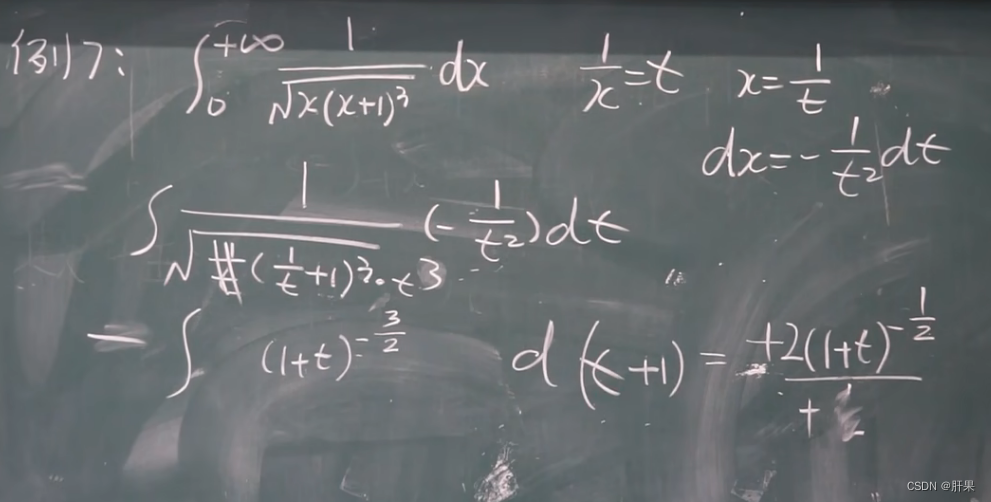
伽马函数

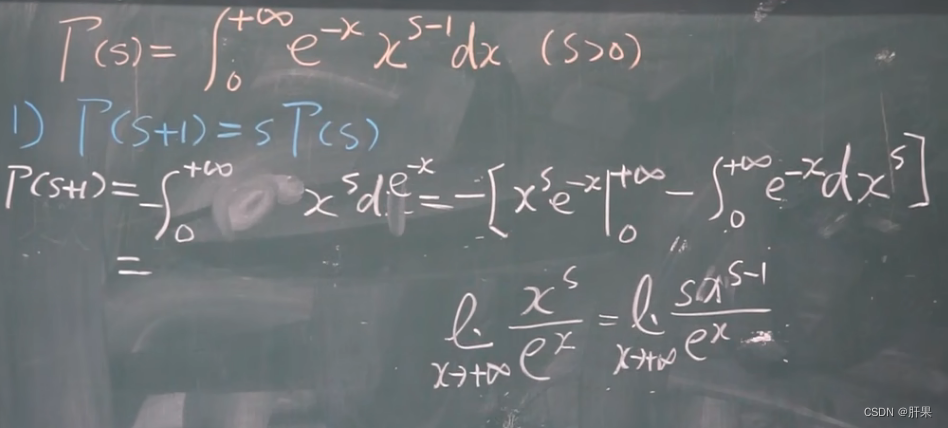
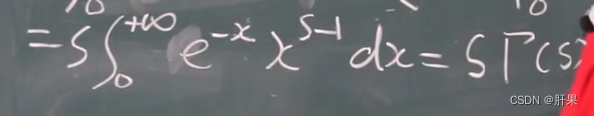
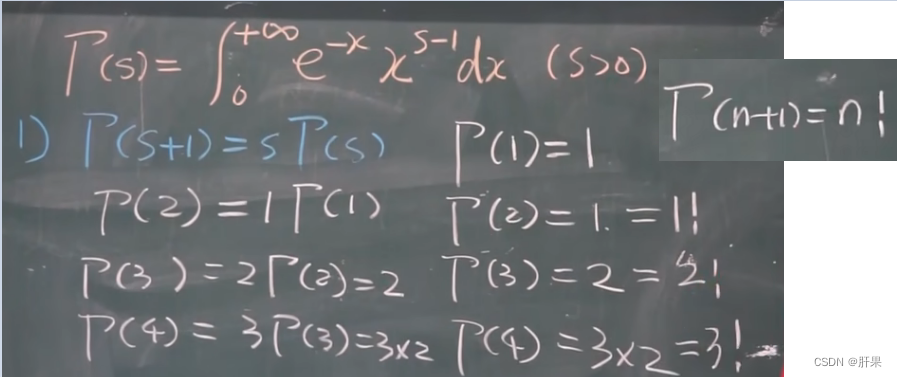
伽马函数是一种特殊函数，通常用符号Γ(x)表示。伽马函数在数学、物理学和工程学等领域中都有重要的应用。

伽马函数的定义式为：

Γ(x) = ∫[0, ∞] t^(x-1)*e(-t) dt

其中x是一个实数，且x>0。

伽马函数的性质如下：

1. Γ(n) = (n-1)!，对于任意正整数n。

2. Γ(x+1) = x * Γ(x)，对于所有的实数x。

3. Γ(1/2) = √π。

伽马函数的应用非常广泛，例如在概率论、统计学中用于计算贝塔分布和F分布的概率密度函数；在物理学中用于计算能级密度、振动频率等；在工程学中用于计算电路中的电流、电压等。