文章目录
- 空间直角坐标系
- 坐标面
- 分向量@坐标分解式
- 余弦定理
- 数量积的坐标表示公式
- 向量积
- 向量积的坐标表示公式
- 向量的外积在物理学中的相关概念
- 物理量
- ref
- 角速度和向量积
- 量纲
- Base unit (measurement)
- Background🎈
- International System of Units🎈
- 附
- 表达方式
- 量纲与单位
- 小结
- 例
空间直角坐标系
- 在空间取定1点O和3个两两垂直的单位向量 i , j , k \boldsymbol{i,j,k} i,j,k,就确定了3条都以O为原点的两两垂直的数轴;三个数轴依次记为 x , y , z x,y,z x,y,z轴,分别称为横轴,纵轴,竖轴,统称为坐标轴(经常用 u u u表示其中的某一个轴)
- 上述元素构成一个空间直角坐标系,称为 O x y z Oxyz Oxyz坐标系或者 [ O ; i , j , k ] [O;\boldsymbol{i,j,k}] [O;i,j,k]坐标系
- 通常将 x , y {x,y} x,y轴配置在水平面上,z轴作为铅垂线
- 它们的正向符合右手规则的是右手系,当右手的四个手指从正向 x x x轴以 π 2 \frac{\pi}{2} 2π角度转向正向y轴时,大拇指的指向就是 z z z轴
坐标面
- 三条坐标轴的任意两条可以构成一个面,这样给出的面称为坐标面,例如,x,y轴确定的平面可以记为
x
O
y
xOy
xOy面
- 类似的有 x O z , y O z xOz,yOz xOz,yOz坐标面
- 三个坐标面将空间分为8个部分,每个部分称为一个卦限
- 分为2层,每层4个卦限,第一个卦限有三个坐标轴的正方向指出
- 从第一卦限开始逆时针编号第一层的四个卦限
- 第5卦限位于第一卦限正下方,从第5卦限开始逆时针编号5~8卦限
分向量@坐标分解式
-
任意向量 r \boldsymbol{r} r,有对应点 M M M,使得 O M → = r \overrightarrow{OM}=\boldsymbol{r} OM=r
-
以 O M OM OM为对角线,三条坐标轴为棱,构建长方体,比如按8个顶点编号为 R H M K − O P N Q RHMK-OPNQ RHMK−OPNQ,前4个字母表示长方体的第一层的4个顶点,后4个字母表示长方体的第二层的4个顶点
-
长方体的面可以有过点M的垂直于坐标面的平面以及3个坐标面相互截取围成的区域
-
设 R , P , Q R,P,Q R,P,Q分别位于 x , y , z x,y,z x,y,z轴上
-
设 O P → = x i \overrightarrow{OP}=x\boldsymbol{i} OP=xi, O Q → = y j \overrightarrow{OQ}=y\boldsymbol{j} OQ=yj, O R → = z k \overrightarrow{OR}=z\boldsymbol{k} OR=zk,则
- r = O M → = x i + y j + z k \boldsymbol{r}=\overrightarrow{OM} =x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k} r=OM=xi+yj+zk
-
上式称为向量 r \boldsymbol{r} r的坐标分解式
-
x i , y j , z k x\boldsymbol{i},y\boldsymbol{j},z\boldsymbol{k} xi,yj,zk称为向量 r \boldsymbol{r} r的沿着3个坐标轴方向的分向量
-
因此在坐标系 O x y z Oxyz Oxyz中,点坐标和向量有一 一对应的关系: r = ( x , y , z ) \boldsymbol{r}=(x,y,z) r=(x,y,z)
-
-
利用坐标作向量的线性运算(加法,减法,数乘)是方便的
- 坐标分解式对用了坐标在各个轴上的分量,不同的向量从坐标分解式的角度理解,容易得到
- a = a x i + a y j + a z k \boldsymbol{a}=a_x\boldsymbol{i}+a_y\boldsymbol{j}+a_z\boldsymbol{k} a=axi+ayj+azk
- b = b x i + b y j + b z k \boldsymbol{b}=b_x\boldsymbol{i}+b_y\boldsymbol{j}+b_z\boldsymbol{k} b=bxi+byj+bzk
- λ a = λ a x i + λ a y j + λ a z k \lambda\boldsymbol{a}=\lambda a_x\boldsymbol{i}+\lambda a_y\boldsymbol{j}+\lambda a_z\boldsymbol{k} λa=λaxi+λayj+λazk
- 坐标分解式对用了坐标在各个轴上的分量,不同的向量从坐标分解式的角度理解,容易得到
-
利用相关交换律和结合律:
- a + b = ( a x + b x ) i + ( a y + b y ) j + ( a z + b z ) k = ( a x + b x , a y + b y , a z + b z ) a − b = ( a x − b x ) i + ( a y − b y ) j + ( a z − b z ) k = ( a x − b x , a y − b y , a z − b z ) λ a = λ ( a x , a y , a z ) \boldsymbol{a+b}=(a_x+b_x)\boldsymbol{i}+(a_y+b_y)\boldsymbol{j}+(a_z+b_z)\boldsymbol{k}=(a_x+b_x,a_y+b_y,a_z+b_z) \\ \boldsymbol{a-b}=(a_x-b_x)\boldsymbol{i}+(a_y-b_y)\boldsymbol{j}+(a_z-b_z)\boldsymbol{k}=(a_x-b_x,a_y-b_y,a_z-b_z) \\ \lambda\boldsymbol{a}=\lambda(a_x,a_y,a_z) a+b=(ax+bx)i+(ay+by)j+(az+bz)k=(ax+bx,ay+by,az+bz)a−b=(ax−bx)i+(ay−by)j+(az−bz)k=(ax−bx,ay−by,az−bz)λa=λ(ax,ay,az)
余弦定理
设在 △ A B C \triangle{ABC} △ABC中, ∠ B C A = θ \angle{BCA}=\theta ∠BCA=θ, ∣ B C ∣ = a |BC|=a ∣BC∣=a, ∣ C A ∣ = b |CA|=b ∣CA∣=b, ∣ A B ∣ = c |AB|=c ∣AB∣=c
-
余弦定理描述的关系式 c 2 = a 2 + b 2 − 2 a b cos θ c^2=a^2+b^2-2ab\cos\theta c2=a2+b2−2abcosθ
-
记 C B → = a \overrightarrow{CB}=\boldsymbol{a} CB=a, C A → = b \overrightarrow{CA}=\boldsymbol{b} CA=b, A B → = c \overrightarrow{AB}=\boldsymbol{c} AB=c,则 c = a − b \boldsymbol{c=a-b} c=a−b
-
从而:
-
∣ c ∣ 2 = c ⋅ c = ( a − b ) ⋅ ( a − b ) = a ⋅ a + b ⋅ b − 2 a ⋅ b = ∣ a ∣ 2 + ∣ b ∣ 2 − 2 ∣ a ∣ ∣ b ∣ cos < a , b > \boldsymbol{ |c|^2=c\cdot{c}=(a-b)\cdot(a-b) =a\cdot{a}+b\cdot{b}-2a\cdot{b} } \\=\boldsymbol{|a|^2+|b|^2}-2\boldsymbol{|a||b|}\cos{\boldsymbol{<a,b>}} ∣c∣2=c⋅c=(a−b)⋅(a−b)=a⋅a+b⋅b−2a⋅b=∣a∣2+∣b∣2−2∣a∣∣b∣cos<a,b>
- 其中 ∣ a ∣ = a |\boldsymbol{a}|=a ∣a∣=a, ∣ b ∣ = b |\boldsymbol{b}|=b ∣b∣=b, ∣ c ∣ = c |\boldsymbol{c}|=c ∣c∣=c, < a , b > = θ \boldsymbol{<a,b>}=\theta <a,b>=θ
- 即 c 2 = a 2 + b 2 − 2 a b cos θ c^2=a^2+b^2-2ab\cos\theta c2=a2+b2−2abcosθ
-
数量积的坐标表示公式
-
设 a = a x i + a y j + a z k \boldsymbol{a}=a_x\boldsymbol{i}+a_y\boldsymbol{j}+a_z\boldsymbol{k} a=axi+ayj+azk; b = b x i + b y j + b z k \boldsymbol{b}=b_x\boldsymbol{i}+b_y\boldsymbol{j}+b_z\boldsymbol{k} b=bxi+byj+bzk
-
根据向量的数量积对加法的分配律:
-
将坐标解析式带入到 a , b \boldsymbol{a,b} a,b,并根据分配律展开
-
a ⋅ b = ( a x i + a y j + a z k ) ⋅ ( b x i + b y j + b z k ) = a x i ⋅ ( b x i + b y j + b z k ) + a y j ⋅ ( b x i + b y j + b z k ) + a z k ⋅ ( b x i + b y j + b z k ) = a x b x i ⋅ i + 0 + 0 + 0 + a y b y j ⋅ j + 0 + 0 + 0 + a z b z k ⋅ k = a x b x + a y b y + a z b z \begin{aligned} \boldsymbol{a\cdot{b}} =&(a_x\boldsymbol{i}+a_y\boldsymbol{j}+a_z\boldsymbol{k}) \cdot (b_x\boldsymbol{i}+b_y\boldsymbol{j}+b_z\boldsymbol{k}) \\ =&a_{x}\boldsymbol{i}\cdot(b_x\boldsymbol{i}+b_y\boldsymbol{j}+b_z\boldsymbol{k})\\ &+a_{y}\boldsymbol{j}\cdot(b_x\boldsymbol{i}+b_y\boldsymbol{j}+b_z\boldsymbol{k})\\ &+a_{z}\boldsymbol{k}\cdot(b_x\boldsymbol{i}+b_y\boldsymbol{j}+b_z\boldsymbol{k}) \\ =&a_xb_x\boldsymbol{i\cdot{i}}+0+0 \\&+0+a_yb_y\boldsymbol{j\cdot{j}}+0 \\&+0+0+a_zb_z\boldsymbol{k\cdot{k}} \\ =&a_xb_x+a_yb_y+a_zb_z \end{aligned} a⋅b====(axi+ayj+azk)⋅(bxi+byj+bzk)axi⋅(bxi+byj+bzk)+ayj⋅(bxi+byj+bzk)+azk⋅(bxi+byj+bzk)axbxi⋅i+0+0+0+aybyj⋅j+0+0+0+azbzk⋅kaxbx+ayby+azbz
- 其中由于 i , j , k \boldsymbol{i,j,k} i,j,k,所以 i ⋅ j = j ⋅ k = i ⋅ k = 0 \boldsymbol{i\cdot{j}=j\cdot{k}=i\cdot{k}}=0 i⋅j=j⋅k=i⋅k=0
- i ⋅ i = j ⋅ j = k ⋅ k = 1 \boldsymbol{i\cdot{i}=j\cdot{j}=k\cdot{k}}=1 i⋅i=j⋅j=k⋅k=1
-
-
向量积
-
研究物体转动问题时,除了考虑物体所受的力,还要分析力所产生的力矩
-
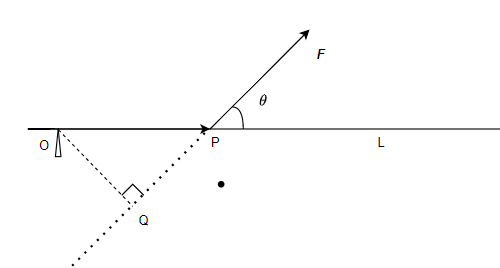
设 O O O为一根杠杆L的支点,有一个力 F \boldsymbol{F} F作用在杠杆上 P P P点处, F \boldsymbol{F} F与 O P → \overrightarrow{OP} OP的夹角为 θ \theta θ,构成的平面记为 Π \Pi Π
-
由力学规定,力 F \boldsymbol{F} F对支点 O O O的力矩是向量 M \boldsymbol{M} M, ∣ M ∣ = ∣ O Q ∣ ∣ F ∣ = ∣ O P → ∣ ∣ F ∣ sin θ |\boldsymbol{M}|=|OQ||\boldsymbol{F}|=|\overrightarrow{OP}||\boldsymbol{F}|\sin{\theta} ∣M∣=∣OQ∣∣F∣=∣OP∣∣F∣sinθ
-
-
M ⊥ Π \boldsymbol{M}\perp{\Pi} M⊥Π, M \boldsymbol{M} M的方向按右手规则从 O P → \overrightarrow{OP} OP以不超过 π \pi π的角度旋转向 F \boldsymbol{F} F来确定
-
当右手的4个手指从 O P → \overrightarrow{OP} OP以不超过 π \pi π的角度转向 F \boldsymbol{F} F握拳时,大拇指的方向就是 M \boldsymbol{M} M的指向
-
从力矩抽象出两个向量的向量积的概念
-
向量 a , b \boldsymbol{a,b} a,b的向量积表示为 c = a × b \boldsymbol{c}=\boldsymbol{a}\times{\boldsymbol{b}} c=a×b,设 θ \theta θ为 a , b \boldsymbol{a,b} a,b的夹角, Π \Pi Π为 a , b \boldsymbol{a,b} a,b所在(决定)的平面
-
模: ∣ c ∣ = ∣ a ∣ ∣ b ∣ sin θ |c|=|\boldsymbol{a}||\boldsymbol{b}|\sin\theta ∣c∣=∣a∣∣b∣sinθ;
-
方向:按右手规则,右手从 a \boldsymbol{a} a向着不超过 π \pi π的一侧夹角转向 b \boldsymbol{b} b时拇指的方向来确定
向量积的坐标表示公式
-
利用结合律和分配律,带入坐标解析式:
-
a × b = ( a x i + a y j + a z k ) × ( b x i + b y j + b z k ) = a x i × ( b x i + b y j + b z k ) + a y j × ( b x i + b y j + b z k ) + a z k × ( b x i + b y j + b z k ) = a x b x ( i × i ) + a x b y ( i × j ) + a x b z ( i × k ) + a y b x ( j × i ) + a y b y ( j × j ) + a y b z ( j × k ) + a z b x ( k × i ) + a z b y ( k × j ) + a z b z ( k × k ) = ( a y b z − a z b y ) i + ( a z b x − a x b z ) j + ( a x b y − a y b x ) k \begin{aligned} \boldsymbol{a\times{b}} =&(a_x\boldsymbol{i}+a_y\boldsymbol{j}+a_z\boldsymbol{k}) \times (b_x\boldsymbol{i}+b_y\boldsymbol{j}+b_z\boldsymbol{k}) \\=&a_{x}\boldsymbol{i}\times(b_x\boldsymbol{i} +b_y\boldsymbol{j}+b_z\boldsymbol{k})\\ &+a_{y}\boldsymbol{j}\times(b_x\boldsymbol{i} +b_y\boldsymbol{j}+b_z\boldsymbol{k})\\ &+a_{z}\boldsymbol{k}\times(b_x\boldsymbol{i} +b_y\boldsymbol{j}+b_z\boldsymbol{k}) \\ =&a_xb_x\boldsymbol{(i\times{i})} +a_xb_y\boldsymbol{(i\times{j})} +a_xb_z\boldsymbol{(i\times{k})} \\ &+a_yb_x\boldsymbol{(j\times{i})} +a_yb_y\boldsymbol{(j\times{j})} +a_yb_z\boldsymbol{(j\times{k})} \\ &+a_zb_x\boldsymbol{(k\times{i})} +a_zb_y\boldsymbol{(k\times{j})} +a_zb_z\boldsymbol{(k\times{k})} \\ =&(a_yb_z-a_zb_y)\boldsymbol{i} +(a_zb_x-a_xb_z)\boldsymbol{j} +(a_xb_y-a_yb_x)\boldsymbol{k} \end{aligned} a×b====(axi+ayj+azk)×(bxi+byj+bzk)axi×(bxi+byj+bzk)+ayj×(bxi+byj+bzk)+azk×(bxi+byj+bzk)axbx(i×i)+axby(i×j)+axbz(i×k)+aybx(j×i)+ayby(j×j)+aybz(j×k)+azbx(k×i)+azby(k×j)+azbz(k×k)(aybz−azby)i+(azbx−axbz)j+(axby−aybx)k
-
其中:
- i × i = j × j = k × k = 0 \boldsymbol{i\times{i}=j\times{j}=k\times{k}}=0 i×i=j×j=k×k=0
- i × j = k \boldsymbol{i\times{j}=k} i×j=k, j × k = i \boldsymbol{j\times{k}=i} j×k=i, i × k = j \boldsymbol{i\times{k}=j} i×k=j
- j × i = − k \boldsymbol{j\times{i}=-k} j×i=−k, k × j = − i \boldsymbol{k\times{j}=-i} k×j=−i, k × i = − j \boldsymbol{k\times{i}=-j} k×i=−j
-
向量的外积在物理学中的相关概念
物理量
- 在物理学中,物理量(英语:physical quantity)是指物质、物体、系统、现象、过程等能用严谨的操作型(可观察、可测量、可操作)定义来度量而可量化的“性质”。
- 经度量出来的结果,称为测量值,其必须以数值和单位(通常偏好国际单位制单位)的积来表达。
- A physical quantity is a physical property of a material or system that can be quantified by measurement.
- A physical quantity can be expressed as a value, which is the algebraic multiplication of a ’ Numerical value ’ and a ’ Unit '.
- For example, the physical quantity of mass can be quantified as '32.3 kg ', where ‘32.3’ is the numerical value and ‘kg’ is the Unit.
- A physical quantity possesses at least two characteristics in common.
- Numerical magnitude
- Units
ref
- Physical quantity - Wikipedia
角速度和向量积
-
角速度(Angular velocity)是在物理学中定义为角位移的变化率,描述物体转动时,在单位时间内转过多少角度以及转动方向的向量,(更准确地说,是赝向量),通常用希腊字母( Ω \Omega Ω)或( ω \omega ω)来表示。
-
在国际单位制中,单位是弧度每秒(rad/s)。在日常生活,通常量度单位时间内的转动周数,即是每分钟转速(rpm),电脑机械硬盘和汽车引擎转数就是以rpm来量度,物理学则以rev/min表示每分钟转动周数。
角速度的方向垂直于转动平面,可通过右手定则来确定,物体以逆时针方向转动其角速度为正值,物体以顺时针方向转动其角速度为负值。 -
角速度量值的大小称作角速率,通常也是用 ω \omega ω来表示。
-
In physics, angular velocity (ω or Ω), also known as angular frequency vector,is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an object rotates or revolves relative to a point or axis).
-
The magnitude of the pseudovector represents" the angular speed", the rate at which the object rotates or revolves, and its direction is normal(垂直) to the instantaneous plane(瞬时平面) of rotation or “angular displacement(角位移)”.
-
The orientation of angular velocity is conventionally specified by the right-hand rule.
-
“orientation”指的是角速度的方向,而“direction”指的是伪矢量的方向,两者在描述物体旋转和伪矢量时所关注的角度略有不同;在描述伪矢量的方向时,我们考虑的是伪矢量与旋转或角位移的瞬时平面之间的垂直关系。它的方向与瞬时平面的法向量是一致的,表示了伪矢量的方向是垂直于旋转或角位移的平面的。
-
There are two types of angular velocity.
-
Orbital angular velocity refers to how fast a point object revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin.
-
Spin angular velocity refers to how fast a rigid body(刚体) rotates with respect to its center of rotation and is independent of the choice of origin, in contrast to orbital angular velocity.自旋角速度是指刚体相对于其自旋中心的旋转速度,与选择的坐标原点无关,与轨道角速度相对立。
-
In general, angular velocity has dimension of angle per unit time (angle replacing distance from linear velocity with time in common).
-
The SI unit of angular velocity is radians per second, with the radian(弧度) being a dimensionless quantity, thus the SI units of angular velocity may be listed as s − 1 s^{−1} s−1. 通常情况下,角速度的量纲为角度每单位时间(用时间取代线性速度中的距离)。角速度的国际单位制单位为弧度每秒,弧度是一个无量纲的量,因此角速度的国际单位制单位可以列为 s − 1 s^{−1} s−1。
角速度通常用符号 omega (ω,有时为 Ω)表示。按照惯例,正的角速度表示逆时针旋转,而负的角速度表示顺时针旋转。
-
Angular velocity is usually represented by the symbol omega (ω, sometimes Ω). By convention, positive angular velocity indicates counter-clockwise rotation, while negative is clockwise.
-
量纲
- 量纲,又叫作因次(英语:base unit 或 fundamental unit),是表示一个物理量由基本量(base quantity)组成的情况。
- 确定若干个基本量后,每个导出量(derived unit)都可以表示为基本量的幂的乘积的形式。
- 引入量纲这一概念可以进行量纲分析,这既是物理学的基础,又有着很多重要应用。
- 量纲包括基本量纲和导出量纲两种。基本量纲是指不能从其他量纲导出的量纲,例如时间、长度、质量等。
- 导出量纲是指由基本量纲通过乘、除、幂运算得到的量纲,例如速度、加速度、力等。
- 在物理学中,量纲的概念非常重要,因为它能够帮助我们理解物理量之间的关系,以及进行单位换算等操作。
- 物理学中,不同的物理量有着不同的单位,然而这些单位之间都有相互的联系。
- 恰当地规定一些基本的单位(称为基本单位),可以使任何其他的单位(称为导出单位)都表达为这些单位的乘积,将其统一以便于研究各个物理量之间的关系。
- 如在国际单位制中,功的单位焦耳( J {\mathrm {J}} J),可以表示为“千克平方米每平方秒”( k g ⋅ m 2 / s 2 {\mathrm {kg\cdot m^{{2}}/s^{{2}}}} kg⋅m2/s2)。
- 仅仅用单位来表示会面临一些问题:
- 在不同的单位制下,各个物理量用单位来表示也会不同,以至于起不到预期的“统一各单位”的效果。
- 如英里每小时(mph)与米每秒(m/s)乍看之下无甚联系,然而它们却都是表示速度的单位。虽然说经过转换可以将各个基本单位也统一,然而这样终究不够直观,需记忆也不甚方便,而且选择哪一个单位作为统一单位似乎都不甚公平。
- 把一个既有的单位表达为拆分了的基本单位的形式实际上没有任何意义
- 功的单位无论如何都不是“千克二次方米每二次方秒”,因为实际上这个单位根本不存在,它只是与“焦耳”恰好相等而已。
- 况且,这样做也会导致一些拆分后相同但实质不同的单位被混淆,如力矩的单位牛米( N ⋅ m {\mathrm {N\cdot m}} N⋅m)被拆分后也是 k g ⋅ m 2 / s 2 {\mathrm {kg\cdot m^{{2}}/s^{{2}}}} kg⋅m2/s2,然而它与功显然是完全不同的。
- 因此量纲被作为表达导出单位组成的专有方式引入物理学中。
Base unit (measurement)
- A base unit (also referred to as a fundamental unit) is a unit adopted for measurement of a base quantity. A base quantity is one of a conventionally chosen subset of physical quantities, where no quantity in the subset can be expressed in terms of the others. The SI base units, or Systeme International d’unites, consists of the metre, kilogram, second, ampere, kelvin, mole and candela.
- A base unit is one that has been explicitly so designated;
- a secondary unit for the same quantity is a derived unit.
- For example, when used with the International System of Units, the “gram” is a derived unit, not a base unit.
Background🎈
- In the language of measurement, physical quantities are quantifiable aspects of the world, such as time, distance, velocity, mass, temperature, energy, and weight, and units are used to describe their magnitude or quantity. Many of these quantities are related to each other by various physical laws, and as a result the units of a quantities can be generally be expressed as a product of powers of other units; for example, momentum is mass multiplied by velocity, while velocity is distance divided by time. These relationships are discussed in dimensional analysis. Those that can be expressed in this fashion in terms of the base units are called derived units.
International System of Units🎈
- In the International System of Units, there are seven base units: kilogram, metre, candela, second, ampere, kelvin, and mole.
附
-
基本单位
-
基本单位(也称为基本量单位)是用于测量基本量的单位。
-
基本量是一组传统意义上选择的物理量的子集,其中子集中的任何一个量都不能用其他量来表示。
-
国际单位制(SI),也称为国际计量单位制,由米、千克、秒、安培、开尔文、摩尔和坎德拉组成。
-
基本单位是明确指定的单位;同一物理量的次要单位是导出单位。例如,在使用国际单位制时,克是一个导出单位,而不是基本单位。
-
-
背景🎈
- 在测量的语境中,物理量是可量化的世界的方面,例如时间、距离、速度、质量、温度、能量和重量,单位用于描述它们的大小或数量。许多这些量之间相互关联,由于这些关系,量的单位通常可以表示为其他单位的幂的乘积;例如,动量是质量乘以速度,而速度是距离除以时间。这些关系在量纲分析中进行了讨论。那些可以用基本单位表示的这种方式来表示的量称为导出单位。
-
国际单位制🎈
- 在国际单位制中,有七个基本单位:千克、米、坎德拉、秒、安培、开尔文、摩尔。
表达方式
- 量纲:将一个物理导出量用若干个基本量的幂之积表示出来的表达式,称为该物理量的量纲乘积式或量纲式,亦简称量纲。
- 规定七个基本物理量,在量纲中分别用七个字母表示它们的量纲,他们是:长度( L {\mathrm {L}} L),质量( M {\mathrm {M}} M),温度( Θ {\mathrm {\Theta }} Θ),电流( I {\mathrm {I}} I),时间( T {\mathrm {T}} T),物质的量( N {\mathrm {N}} N),发光强度( J {\mathrm {J}} J)。
- 则对于任意一个物理量
A
A
A,都可以写出下列量纲式:(物理量A的量纲)
- dim A = L α M β Θ γ I δ T ϵ N ζ J η {\displaystyle \dim A=\mathrm {L^{\alpha }\,M^{\beta }\,\Theta ^{\gamma }\,I^{\delta }\,T^{\epsilon }\,N^{\zeta }\,J^{\eta }} } dimA=LαMβΘγIδTϵNζJη
- 等号左边也可以表示为 [ A ] \left[A\right] [A]
- 上式右边称为物理量 A A A的量纲。其中, α , β , γ , δ , ϵ , ζ , η \alpha ,\beta ,\gamma ,\delta ,\epsilon ,\zeta ,\eta α,β,γ,δ,ϵ,ζ,η称为量纲指数。
- 在表示时,七个量纲不一定会全部用上。
- 量纲指数为1的可以省略指数,指数为0的可以省略对应量纲;
- 然而,当所有量纲指数皆为0时(称为无量纲),要将量纲记为“1”。
- 对于功, dim W = L 2 M T − 2 \dim W={\mathrm {L^{{2}}MT^{{-2}}}} dimW=L2MT−2
- 对于磁感应强度, dim B = M T − 2 I − 1 \dim B={\mathrm {MT^{{-2}}I^{{-1}}}} dimB=MT−2I−1
- 对于弧度, dim θ = 1 \dim \theta ={\mathrm {1}} dimθ=1
量纲与单位
- 值得注意的是,虽然物理量的量纲与取什么单位无关,但量纲却只有在一定的单位制下才有意义
小结
- 物理量是用来描述物理现象的性质或量度的概念。例如,长度、质量、时间、温度、电流等都是物理量。每一个物理量都具有一个数值和一个单位来表示其大小。
- 单位是用来度量物理量的度量标准。它们可以是基本单位,例如米、千克、秒等,也可以是导出单位,通过基本单位的组合来表示其他物理量。单位的选择和定义是通过国际单位制(SI)进行统一。
- 量纲是用来描述物理量之间的关系和归类的指标。量纲基于基本物理量(长度、质量、时间、电流、温度、物质的量、发光强度)的幂次乘积来表示物理量。每一个物理量都有一个特定的量纲,它通过量纲指数来表示。
- 物理量、单位和量纲之间的关系可以总结如下:物理量的大小由数值和单位来表示,而量纲则描述了物理量之间的关系。单位和量纲的选择要符合国际单位制的规定 。通过量纲分析可以检验方程或计算结果的合理性,以确保物理理论的正确性。
例
- 设刚体以等角速度 ω \boldsymbol\omega ω绕 l l l轴旋转,计算刚体上一点 M M M的线速度 v \boldsymbol{v} v的大小
- 设点 M M M到 l l l的距离为 a a a,再在 l l l上任取一点 O O O作向量 m = O M → \boldsymbol{m}=\overrightarrow{OM} m=OM,并以 θ \theta θ表示 ω \boldsymbol{\omega} ω与 m \boldsymbol{m} m的夹角,则 a = ∣ m ∣ sin θ a=|\boldsymbol{m}|\sin{\theta} a=∣m∣sinθ,刚体旋转半径为 a a a
- 根据物理学中线速度和角速度的关系:
v
=
ω
a
v=\omega{a}
v=ωa可知:
∣
v
∣
=
∣
w
∣
∣
m
∣
sin
θ
|\boldsymbol{v}|=|\boldsymbol{w}||\boldsymbol{m}|\sin\theta
∣v∣=∣w∣∣m∣sinθ
- 其中 v \boldsymbol{v} v的方向垂直于同时过点 M M M与轴 l l l的平面,即向量 ω , m \boldsymbol{\omega,m} ω,m所在的平面(描述空间中的直线的方向需要足够精准)
- 因此, v = ω × m \boldsymbol{v}=\boldsymbol{\omega\times{m}} v=ω×m