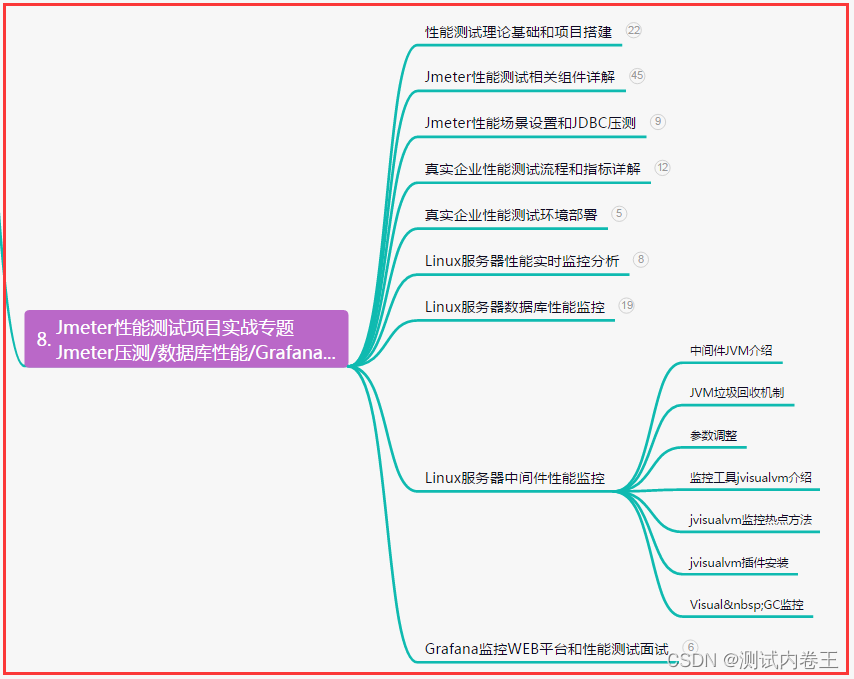
冻龟算法系列之路径问题
文章目录
- 【动态规划】路径问题
- 1. 不同路径
- 1.1 题目解析
- 1.2 算法原理
- 1.2.1 状态表示
- 1.2.2 状态转移方程
- 1.2.3 初始化
- 1.2.4 填表顺序
- 1.2.5 返回值
- 1.3 编写代码
- 2. 不同路径Ⅱ
- 2.1 题目解析
- 2.2 算法原理
- 2.2.1 状态表示
- 2.2.2 状态转移方程
- 2.2.3 初始化
- 2.2.4 填表顺序
- 2.2.5 返回值
- 2.3 编写代码
- 3. 礼物的最大价值
- 3.1 题目解析
- 3.2 算法原理
- 3.2.1 状态表示
- 3.2.2 状态转移方程
- 3.2.3 初始化
- 3.2.4 填写顺序
- 3.2.5 返回值
- 3.3 编写代码
- 4. 下降路径最小和
- 4.1 题目解析
- 4.2 算法原理
- 4.2.1 状态表示
- 4.2.2 状态转移方程
- 4.2.3 初始化
- 4.2.4 填表顺序
- 4.2.5 返回值
- 4.3 编写代码
- 5. 最小路径和
- 5.1 题目解析
- 5.2 算法原理
- 5.2.1 状态表示
- 5.2.2 状态转移方程
- 5.2.3 初始化
- 5.2.4 填表顺序
- 5.2.5 返回值
- 5.3 编写代码
- 6. 地下城游戏
- 6.1 题目解析
- 6.2 算法原理
- 6.2.1 状态表示
- 6.2.2 状态转移方程
- 6.2.3 初始化
- 6.2.4 填表顺序
- 6.2.5 返回值
- 6.3 编写代码
【动态规划】路径问题
本文为动态规划的第二章:路径问题,重点讲解关于路径有关的问题,上一篇文章是一维的,那么路径问题就是二维的,通过题目可见需要创建二维的dp表,而以下将通过“解题”的方式去学习动归知识!
- 创建什么样的dp表,其实看题目就可以看出来了,一般根据题目原有意境/数据结构
动态规划基础博客:【动态规划】斐波那契数列模型_s:103的博客-CSDN博客
1. 不同路径
传送门:力扣92
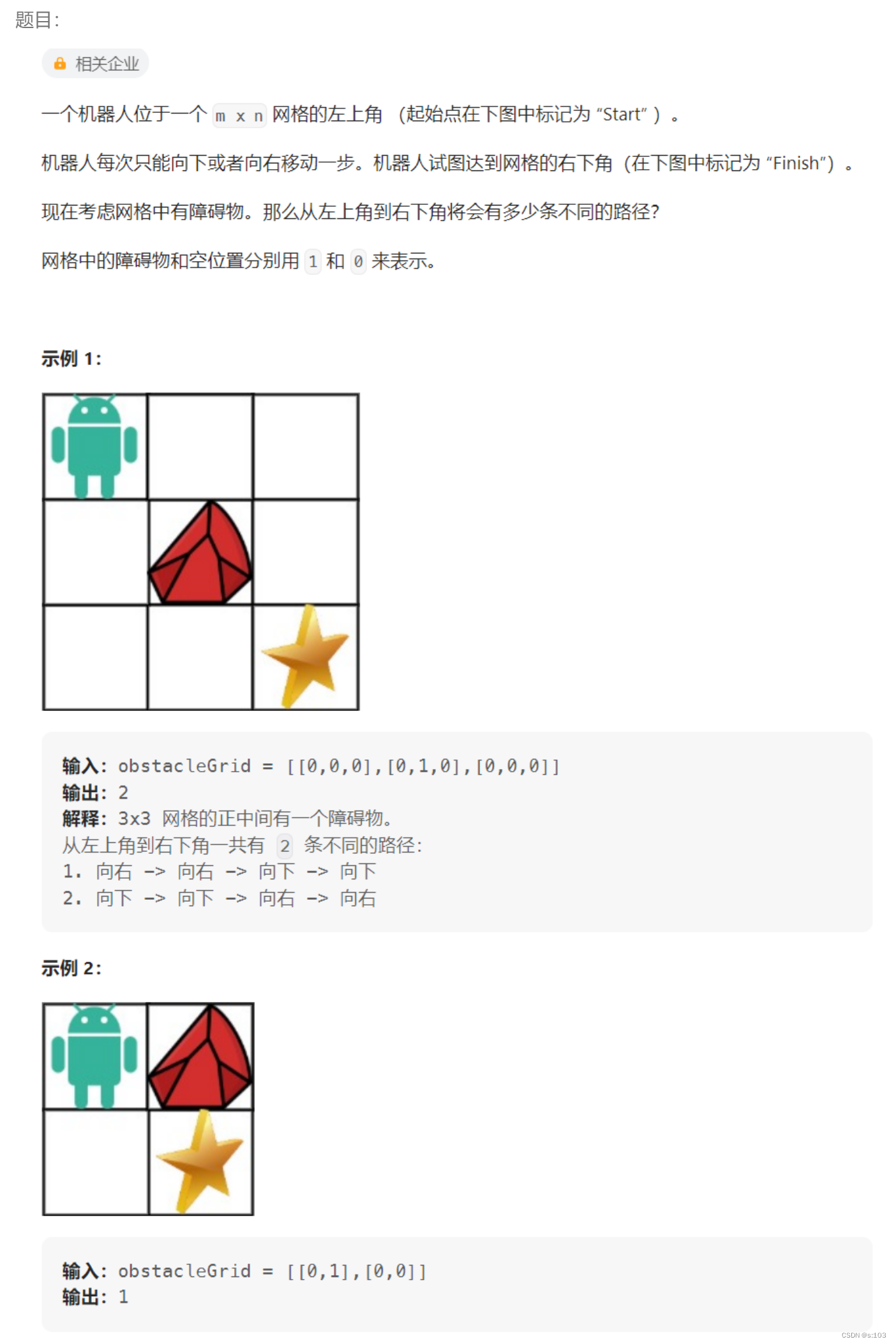
题目:
1.1 题目解析
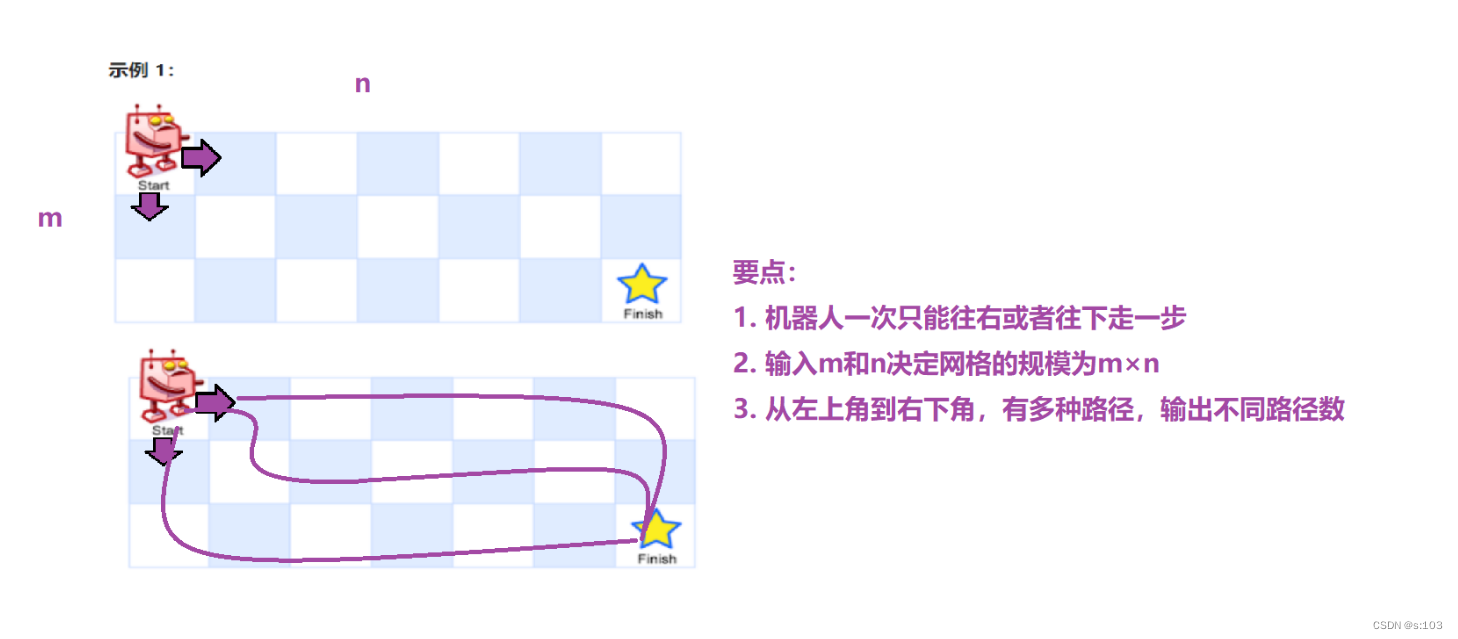
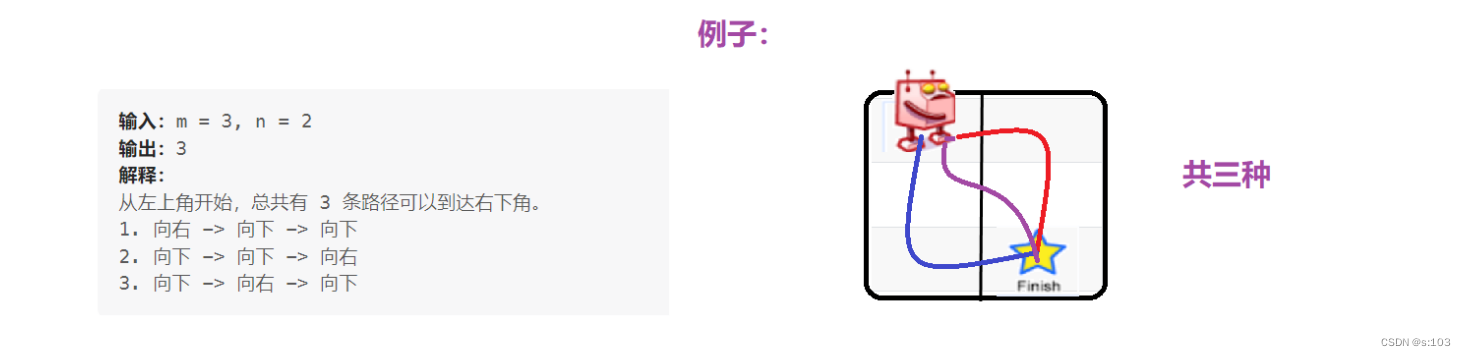
越难的dp问题,看示例只能起到了解题目的效果,一般推不出啥普遍的规律,所以接下来就是我们的算法原理,通过动归的思想去理解,才会豁然开朗!
1.2 算法原理
1.2.1 状态表示
我们需要通过经验 + 题目要求去决定状态表示:
- 根据题目的意境以及数据结构,我们得出需要建立二维dp表
- 经验:以某个坐标为结尾或者以某个坐标为起点去研究题目问题!
- 此题用的是“结尾”
再根据经验,一般dp表的其中一值就应该是答案!
- 所以含义应该就是“路径数”
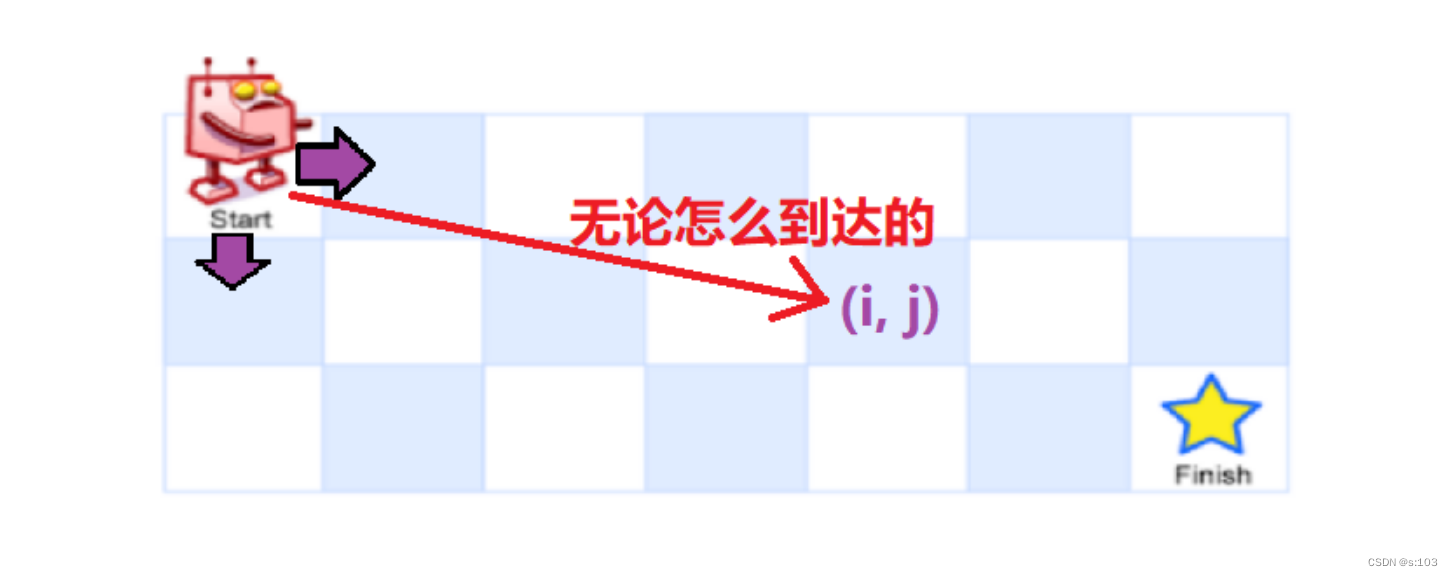
综合得到状态表示:dp[i][j]表示表示的就是起点到坐标为(i, j)的位置的路径数
1.2.2 状态转移方程
同样的套路,我们需要根据已确定的dp表的值来推导dp[i] [j]的值,并且牢记dp表的状态表示!
- 我们以(i, j)为结尾
- 根据“最近一步”去划分问题
“最近一步”可以理解为“必然事件”
- 此题的“必然事件”就是,到达(i, j)之前,必然要先到达(i - 1, j)或者(i, j -1)
- 先到达(i - 1, j)的话,路径数为dp[i - 1] [j],到达(i, j)为每条路径的最后一步(注意:并不是路径数加1,因为这一步是每种情况统一的最后一步而已)
- 先到达(i, j - 1)的话,路径数为dp[i] [j - 1],到达(i, j)为每条路径的最后一步
那么dp[i] [j]就是为这两种情况的路径数之和!
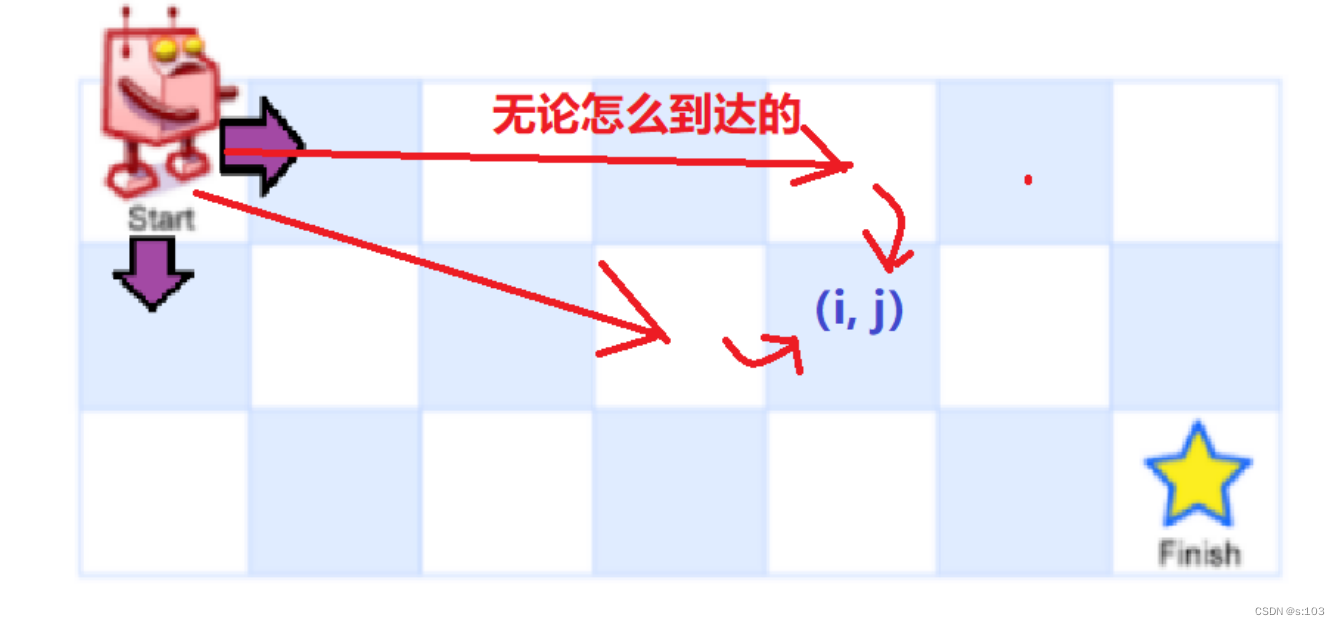
所以得出状态转移方程:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
1.2.3 初始化
对于这道题的状态表示和状态转移方程,有以下坐标(桃心标记)在填表的时候会出现异常:
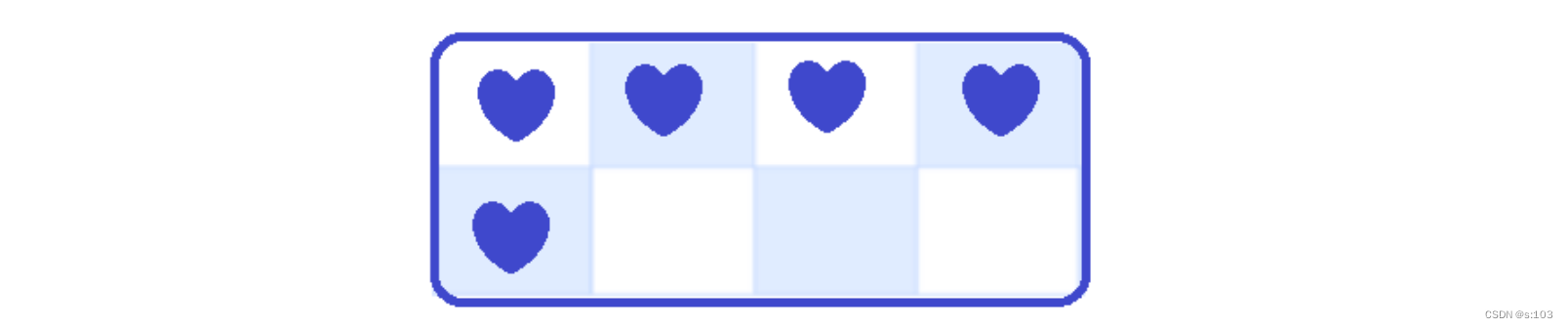
因为我们的状态转移方程需要访问到左边一格和上面一格的元素,而在这个边界,会越界
- 在这里,我们可以选择单独给这一行一列去赋值,但是在往后的学习中,这一种做法会比较复杂,代码不太美观等等…
- 所以这里提供一个技巧,就是扩张矩阵,利用假数据(上一篇文章有提到),
- 注意事项:
- 添加的假数据在填表时不影响其真实值
- 下标对应(因为矩阵扩张,坐标发送变化)
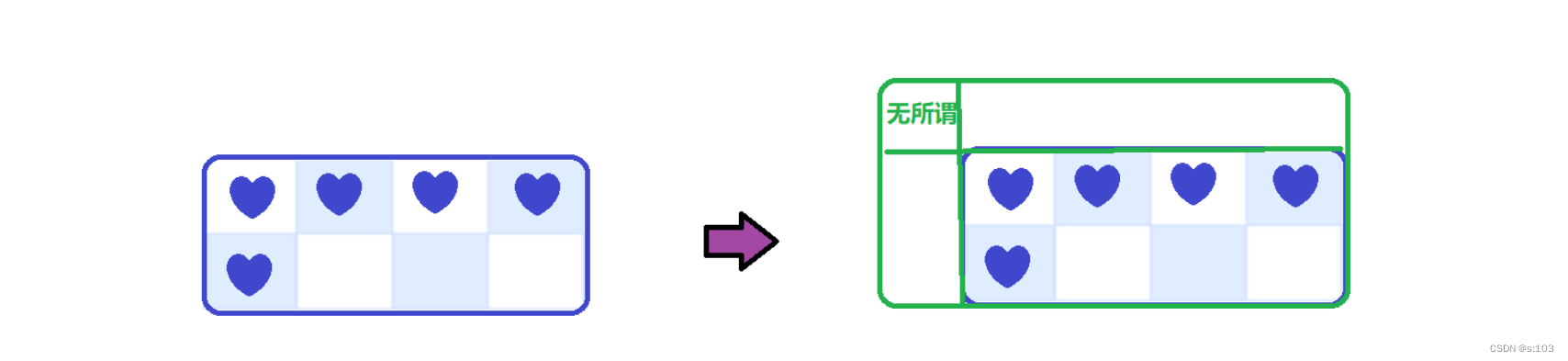
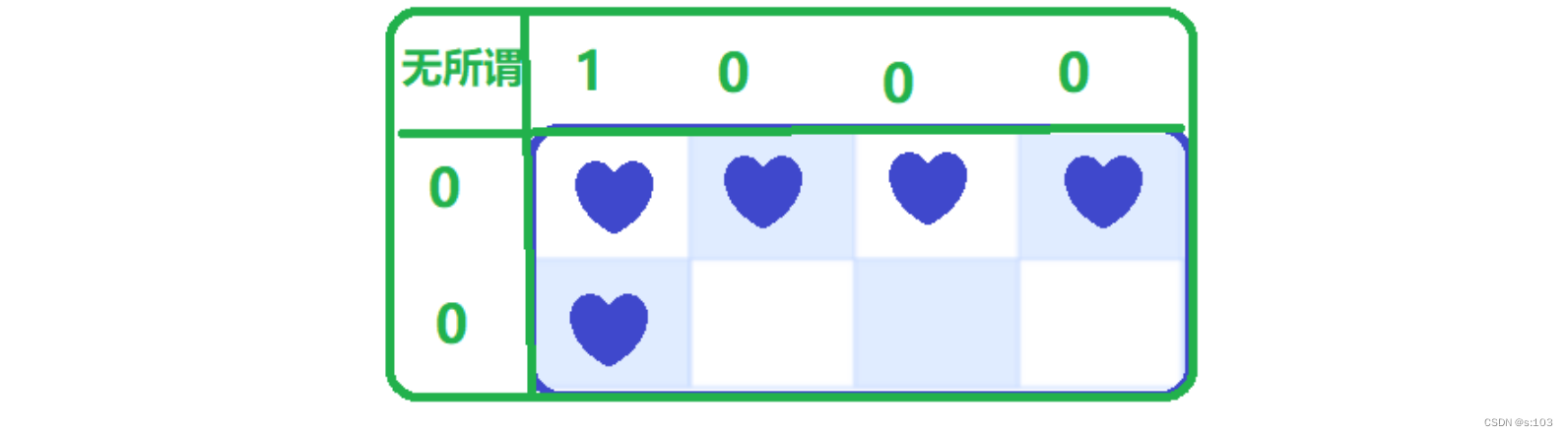
- 现坐标为(1, 1)的dp值,应该为1,所以(0, 1)或者(1, 0)有一个为1就行
- 其他的假数据为0就行了,因为不能影响其真实值!
1.2.4 填表顺序
总的来看是:左上角到右下角
- 即从上到下每一行,每一行从左到右,保证所需要利用的dp值是填过的!
1.2.5 返回值
注意下标对应!
由于我们扩展了矩阵,所以坐标发生了变化,原(0, 0) 变成 现(1, 1)
则我们的返回值为dp(m, n)
- 数组大小为:(m + 1) × (n + 1)
1.3 编写代码
- 根据算法原理编写代码即可:
- 创建dp表
- 初始化,处理边界问题
- 填表
- 返回值
class Solution {
public int uniquePaths(int m, int n) {
//1. 建立dp表
//2. 初始化
//3. 填表
//4. 返回值
int[][] dp = new int[m + 1][n + 1];
dp[0][1] = 1;
for(int i = 1; i < m + 1; i++) {
for(int j = 1; j < n + 1; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
}
- 注意下标对应!
时空复杂度都为:O(N2)
2. 不同路径Ⅱ
传送门:力扣93
题目:
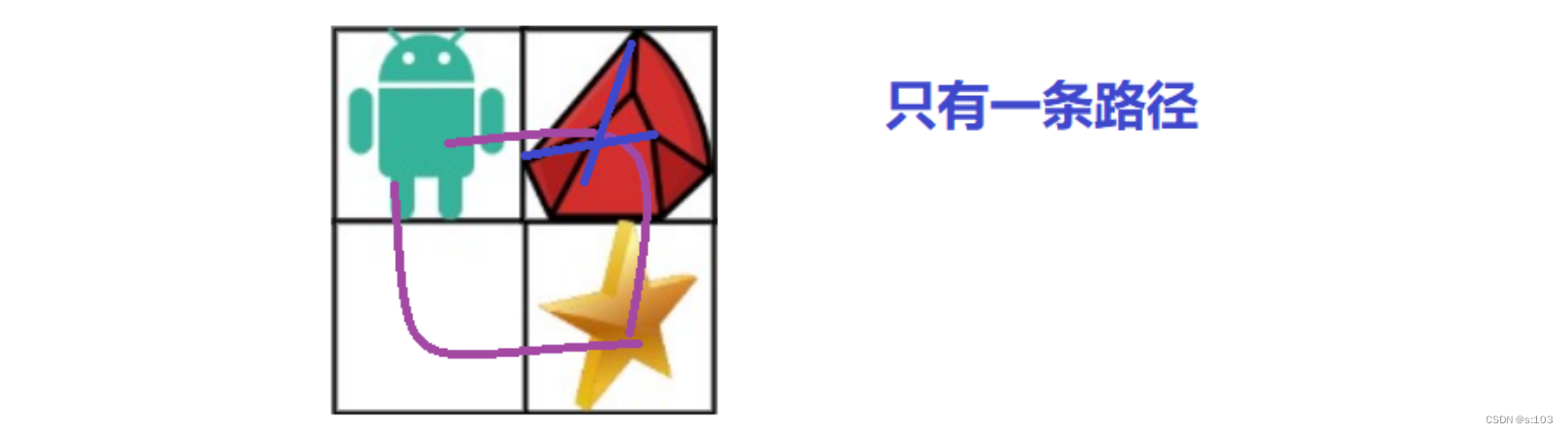
2.1 题目解析

2.2 算法原理
2.2.1 状态表示
我们需要通过经验 + 题目要求去决定状态表示:
- 根据题目的意境以及数据结构,我们得出需要建立二维dp表
- 经验:以某个坐标为结尾或者以某个坐标为起点去研究题目问题!
- 此题用的是“结尾”
再根据经验,一般dp表的其中一值就应该是答案!
- 所以含义应该就是**“路径数”**
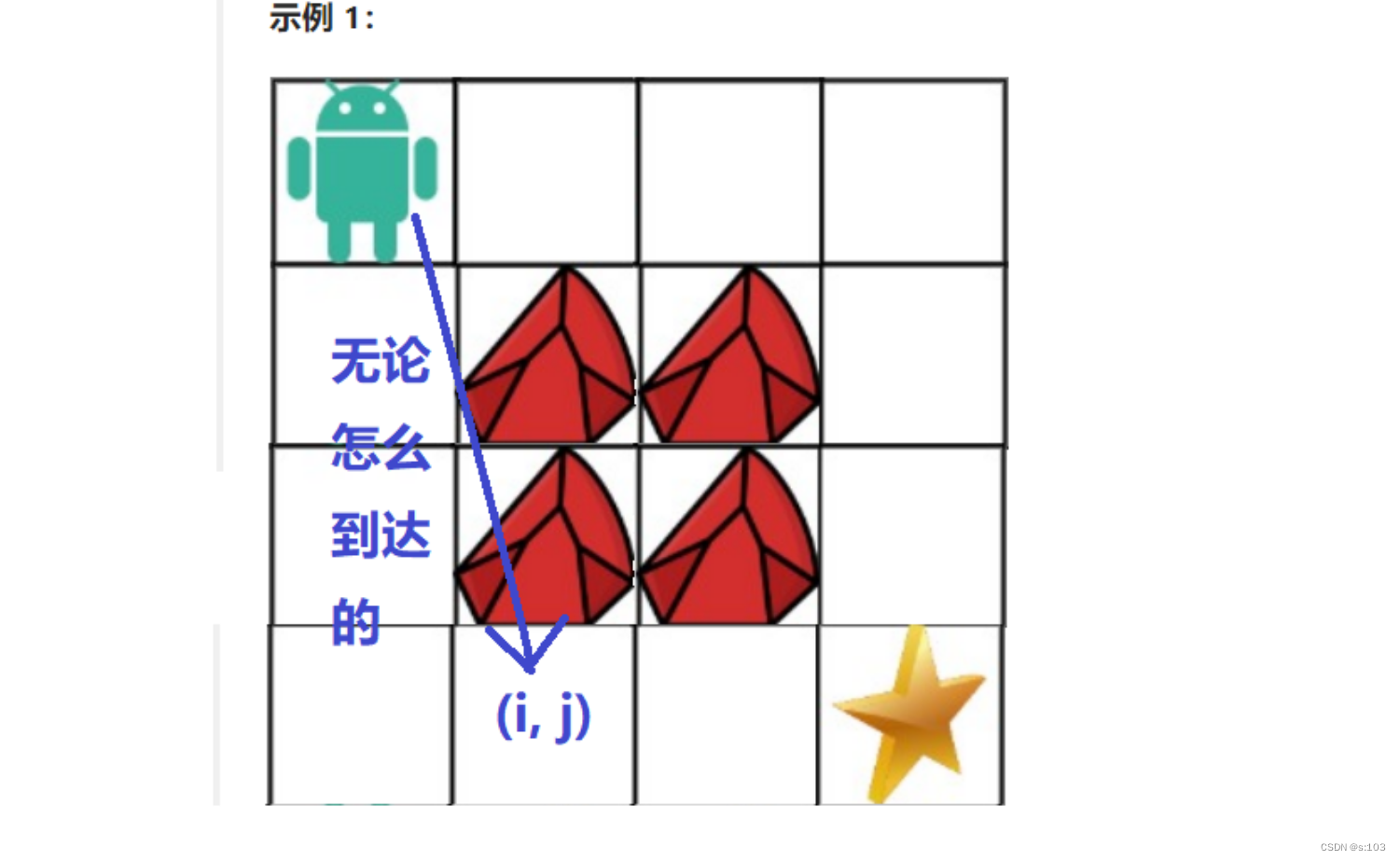
综合得到状态表示:dp[i][j]表示表示的就是起点到坐标为(i, j)的位置的路径数
2.2.2 状态转移方程
同样的套路,我们需要根据已确定的dp表的值来推导dp[i] [j]的值,并且牢记dp表的状态表示!
- 我们以(i, j)为结尾
- 根据“最近一步”去划分问题
“最近一步”可以理解为“必然事件”
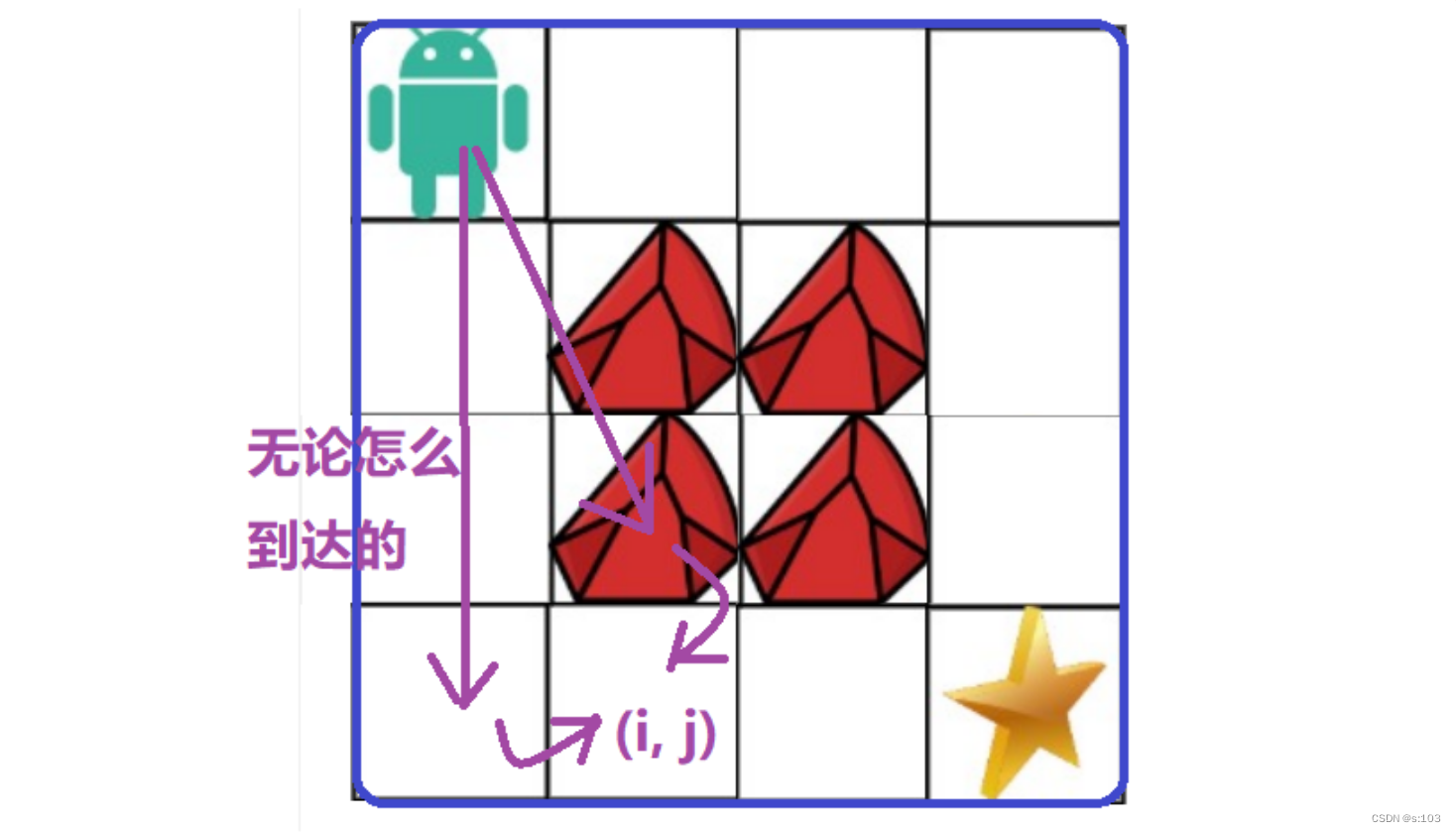
- 此题的“必然事件”就是,到达(i, j)之前,必然要先到达(i - 1, j)或者(i, j -1)
- 先到达(i - 1, j)的话,路径数为dp[i - 1] [j],到达(i, j)为每条路径的最后一步(注意:并不是路径数加1,因为这一步是每种情况统一的最后一步而已)
- 先到达(i, j - 1)的话,路径数为dp[i] [j - 1],到达(i, j)为每条路径的最后一步
那么dp[i] [j]就是为这两种情况的路径数之和!
到这里,仍然跟第一道题一致,但是此题多出的要点,要考虑到状态转移方程!
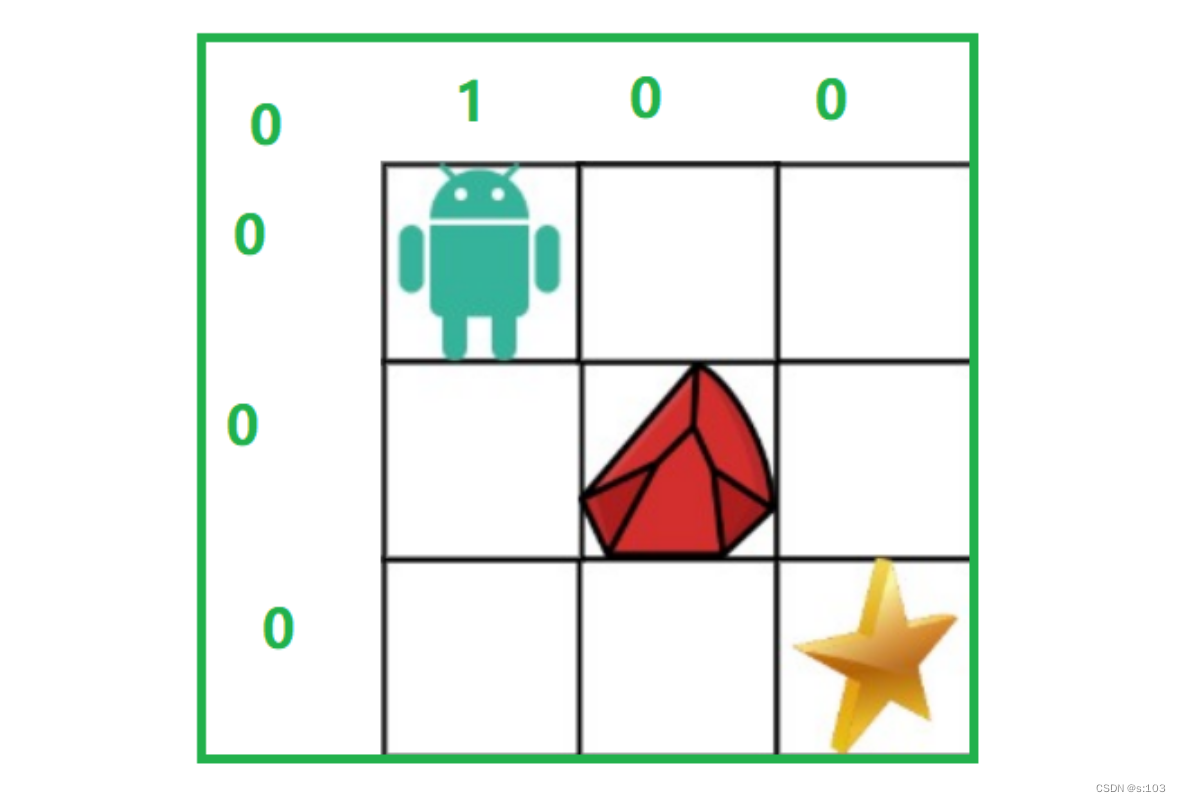
也就是说,如果(i, j)为障碍物,则最后一步将不构成一条路径,也就是说无论(i, j - 1)还是(i - 1, j)路径数再多,都不能到达(i, j),所以dp值应该为0!

- 所以通过o这个二维数组判断是否有障碍物(0代表无,1代表有)
所以得出状态转移方程:dp[i][j] = o[i][j] == 0 ? dp[i - 1][j] + dp[i][j - 1] : 0;
2.2.3 初始化
同样的,进行扩张矩阵 => (m + 1) ×(n + 1)大小
- 假数据不能影响真实值
- 下标对应问题
2.2.4 填表顺序
- 从左上角到右下角:从上到下每一行,每一行从左到右
2.2.5 返回值
下标对应:返回dp[m] [n]
2.3 编写代码
class Solution {
public int uniquePathsWithObstacles(int[][] o) {
//1. 创建dp表
//2. 初始化
//3. 填表
//4. 返回值
int m = o.length;
int n = o[0].length;
int[][] dp = new int[m + 1][n + 1];
dp[0][1] = 1;
for(int i = 1; i < m + 1; i++) {
for(int j = 1; j < n + 1; j++) {
dp[i][j] = o[i - 1][j - 1] == 0 ? dp[i][j - 1] + dp[i - 1][j] : 0;
}
}
return dp[m][n];
}
}

- 注意下标对应!
3. 礼物的最大价值
传送门:力扣剑指offer47
题目:
3.1 题目解析

3.2 算法原理
3.2.1 状态表示
我们需要通过经验 + 题目要求去决定状态表示:
- 根据题目的意境以及数据结构,我们得出需要建立二维dp表
- 经验:以某个坐标为结尾或者以某个坐标为起点去研究题目问题!
- 此题用的是“结尾”
再根据经验,一般dp表的其中一值就应该是答案!
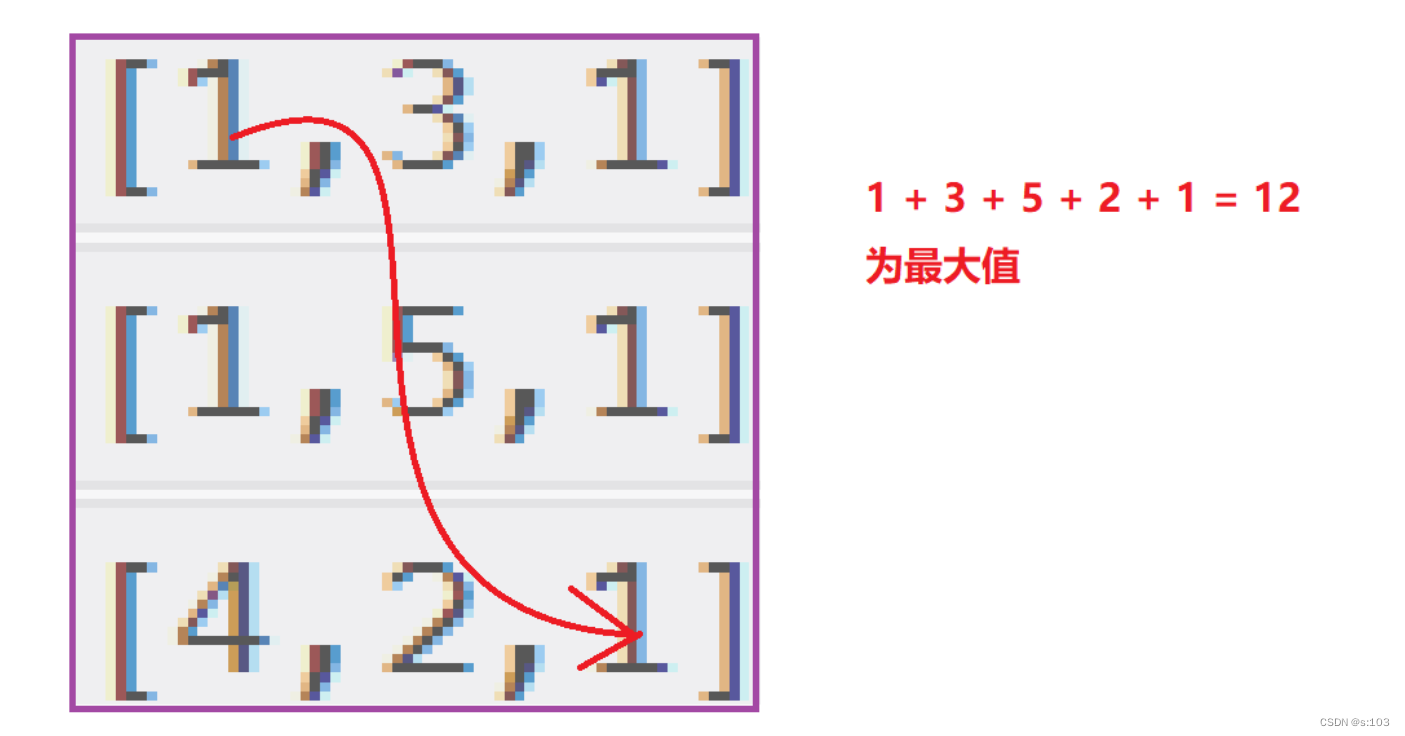
- 所以含义应该就是“路径最大价值”
综合得到状态表示:dp[i][j]表示表示的就是起点到坐标为(i, j)的位置的路径最大价值
3.2.2 状态转移方程
同样的套路,我们需要根据已确定的dp表的值来推导dp[i] [j]的值,并且牢记dp表的状态表示!
- 我们以(i, j)为结尾
- 根据“最近一步”去划分问题
“最近一步”可以理解为“必然事件”
- 此题的“必然事件”就是,到达(i, j)之前,必然要先到达(i - 1, j)或者(i, j -1)
- 先到达(i - 1, j)的话,起点到达(i, j)的价值为dp[i - 1] [j] + grid[i] [j]
- 先到达(i, j - 1)的话,起点到达(i, j)的价值为dp[i] [j - 1] + grid[i] [j]
那么dp[i] [j]就是为这两种情况的较大值!
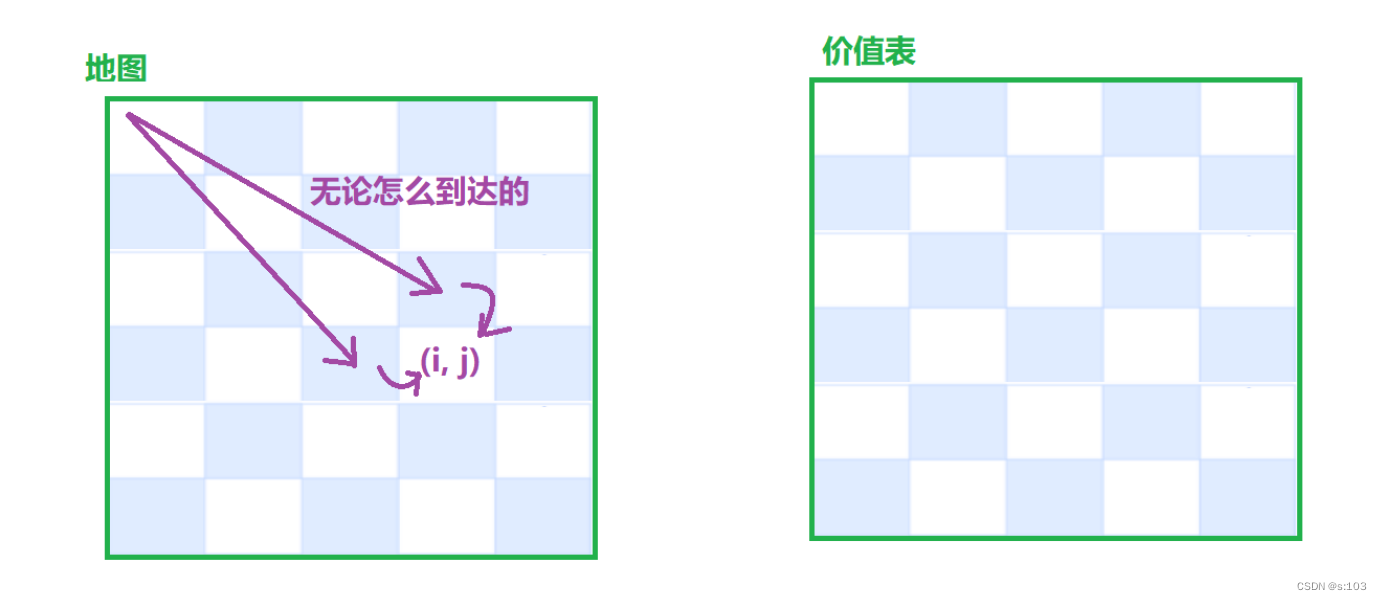
得出状态转移方程:dp[i][j] = max{dp[i][j - 1], dp[i - 1][j]} + grid[i][j]
3.2.3 初始化
老样子,扩张矩阵为 (m + 1)×(n + 1)
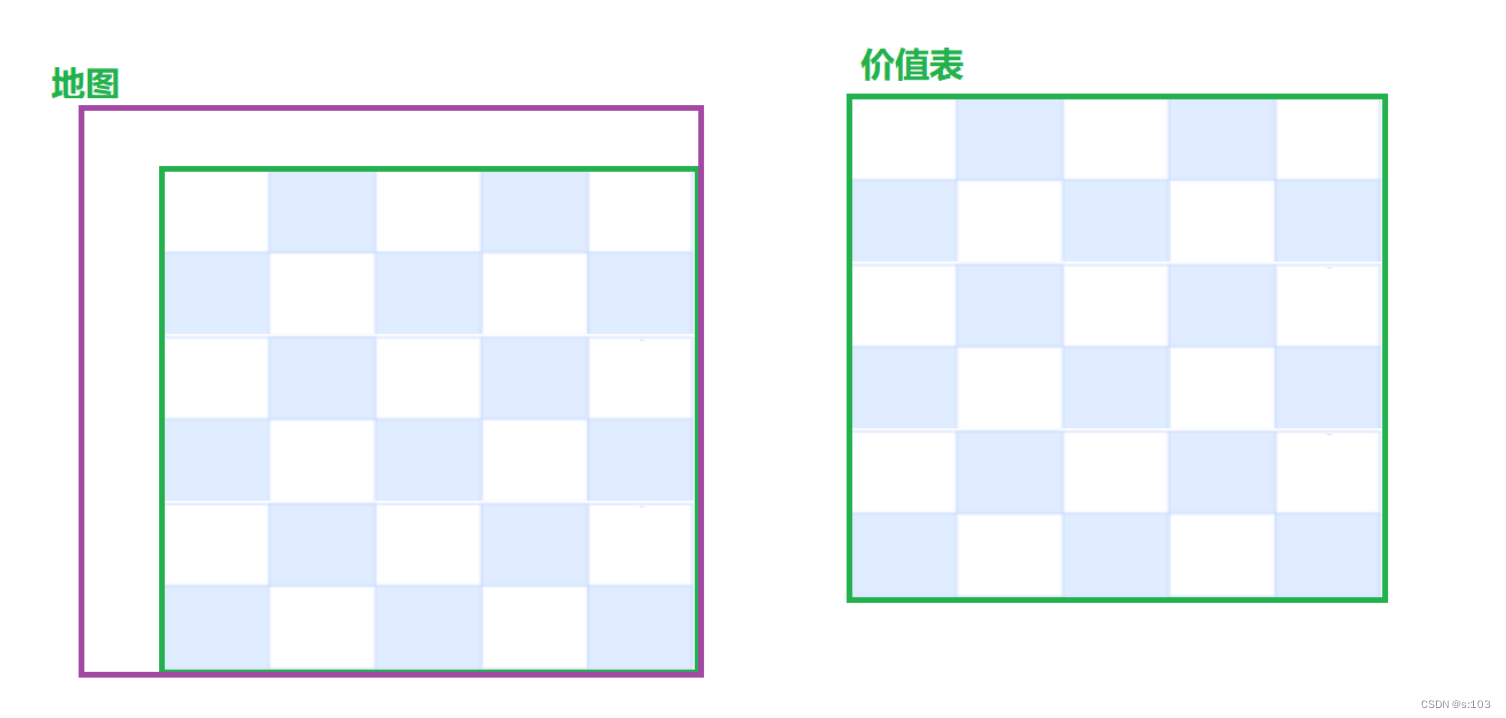
- 假数据不能影响真实值
- 由于礼物值大于等于0,所以假数据设置0就不会影响了(原本是要 “-∞”)
- 其中(0, 1)和(1, 0)必须为0
- 下标对应问题
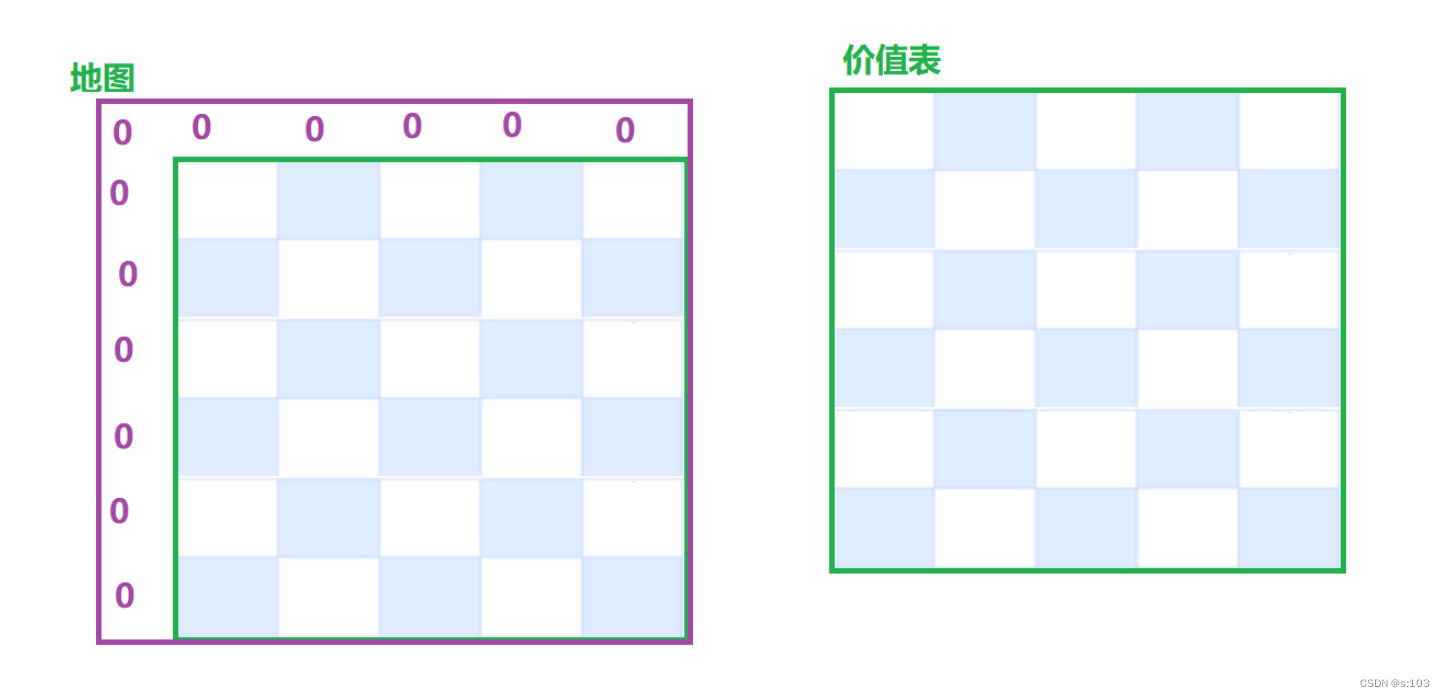
3.2.4 填写顺序
从左上角到右下角:从上到下每一行,每一行从左到右
3.2.5 返回值
根据下标对应:应该返回dp[m] [n]
3.3 编写代码
class Solution {
public int maxValue(int[][] grid) {
//1. 创建dp表
//2. 初始化
//3. 填表
//4. 返回值
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m + 1][n + 1];
for(int i = 1; i < m + 1; i++) {
for(int j = 1; j < n + 1; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
}
}
return dp[m][n];
}
}

- 一定要注意下标对应!
4. 下降路径最小和
传送门:力扣931
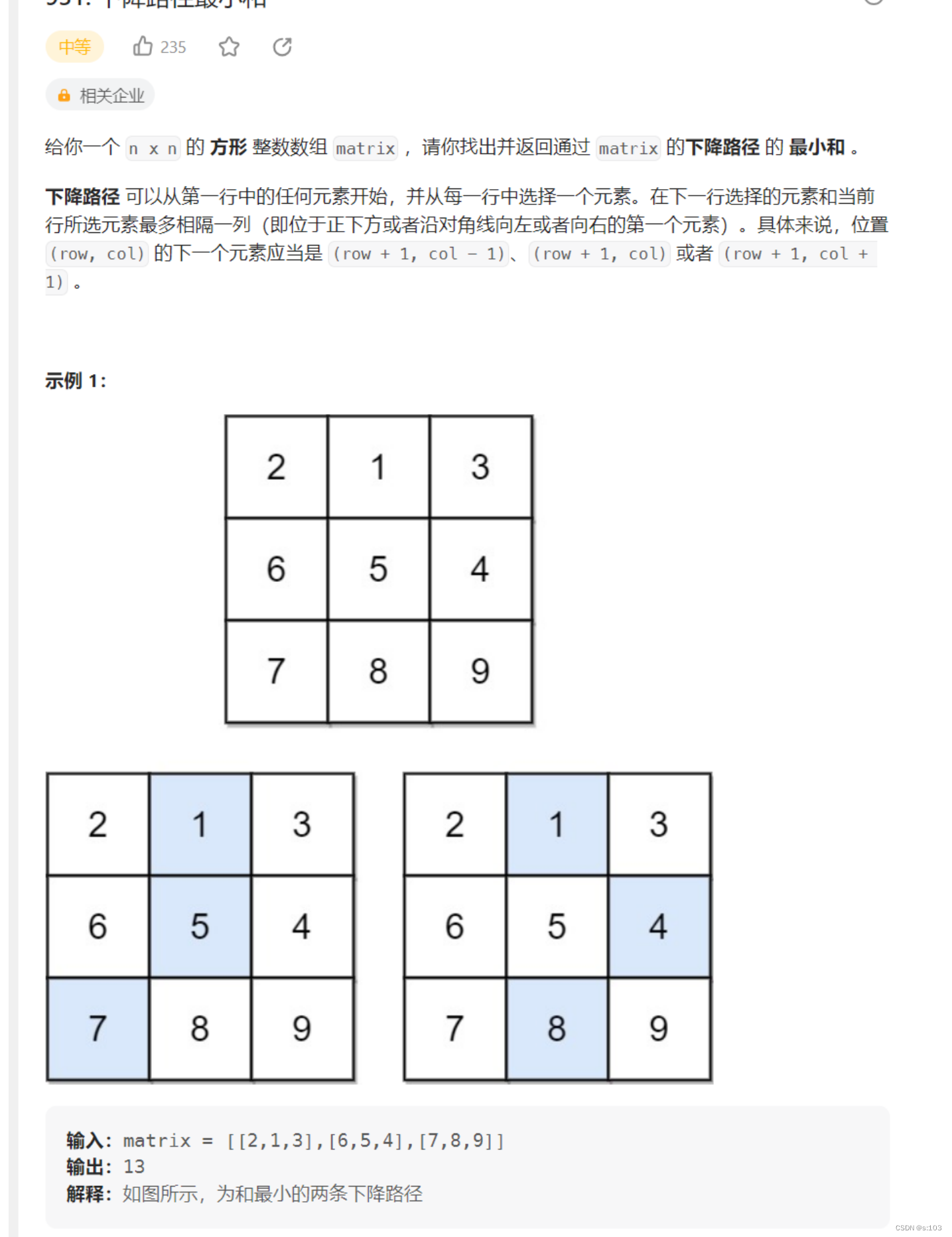
题目:
4.1 题目解析
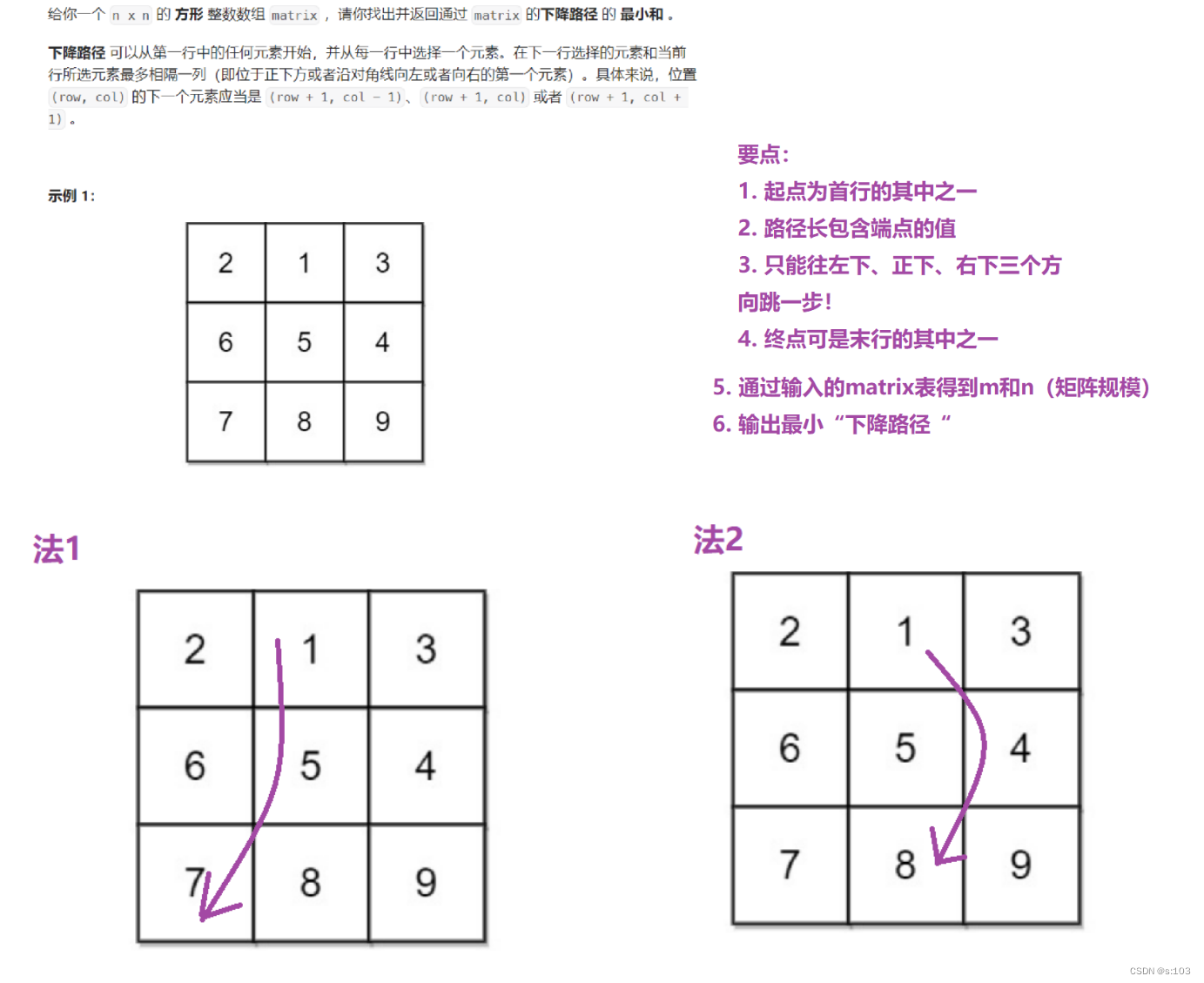
4.2 算法原理
4.2.1 状态表示
我们需要通过经验 + 题目要求去决定状态表示:
- 根据题目的意境以及数据结构,我们得出需要建立二维dp表
- 经验:以某个坐标为结尾或者以某个坐标为起点去研究题目问题!
- 此题用的是“结尾”
再根据经验,一般dp表的其中一值就应该是答案!
- 所以含义应该就是“最小下降路径长”
综合得到状态表示:dp[i][j]表示表示的就是“起点”到坐标为(i, j)的位置的最小下降路径长
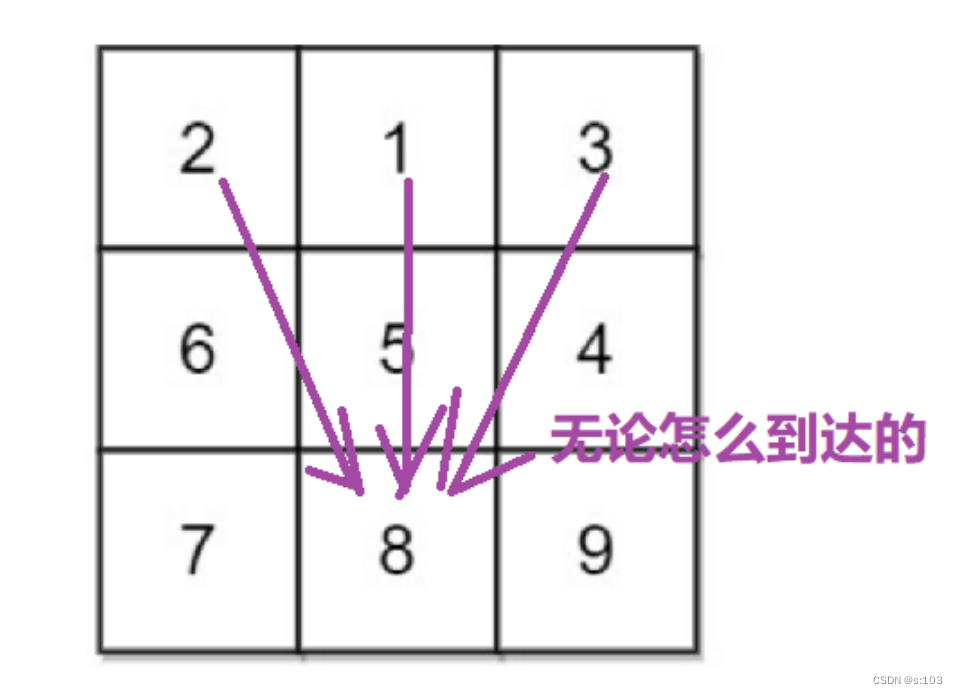
4.2.2 状态转移方程
同样的套路,我们需要根据已确定的dp表的值来推导dp[i] [j]的值,并且牢记dp表的状态表示!
- 我们以(i, j)为结尾
- 根据“最近一步”去划分问题
“最近一步”可以理解为“必然事件”
- 此题的“必然事件”就是,到达(i, j)之前,必然要先到达(i - 1, j)或者(i - 1, j -1)或者(i - 1, j + 1)
- 先到达(i - 1, j)的话,起点到达(i, j)的下降路径长为dp[i - 1] [j] + matrix[i] [j]
- 先到达(i - 1, j -1)的话,起点到达(i, j)的下降路径长为dp[i - 1] [j - 1] + matrix[i] [j]
- 先到达(i - 1, j + 1)的话,起点到达(i, j)的下降路径长为dp[i - 1] [j + 1] + matrix[i] [j]
那么dp[i] [j]就是为这三种情况的较小值
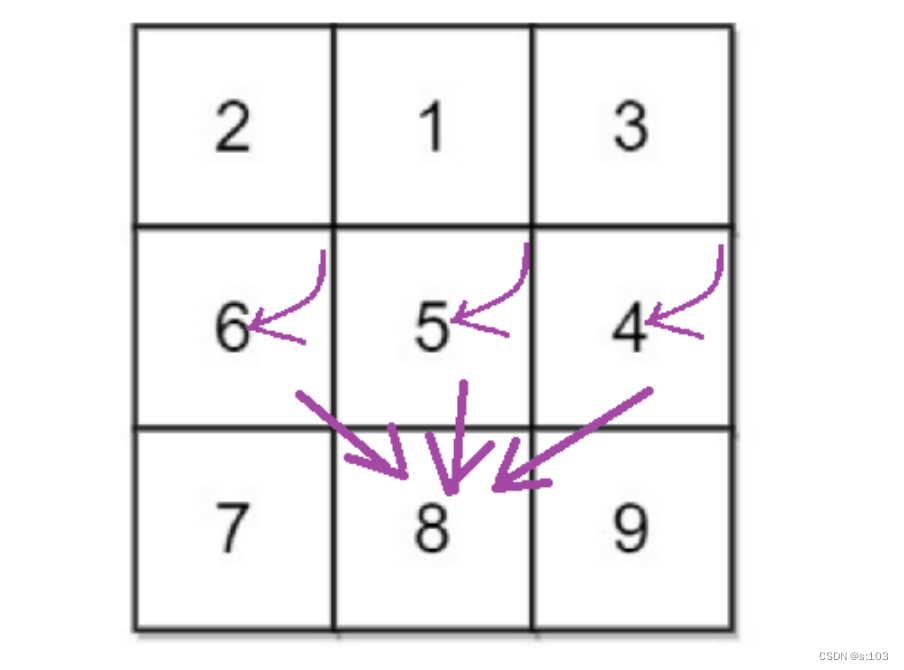
得到状态转移方程:dp[i][j] = min{dp[i - 1][j], dp[i - 1][j - 1], dp[i - 1][j + 1]} + matrix[i][j];
4.2.3 初始化
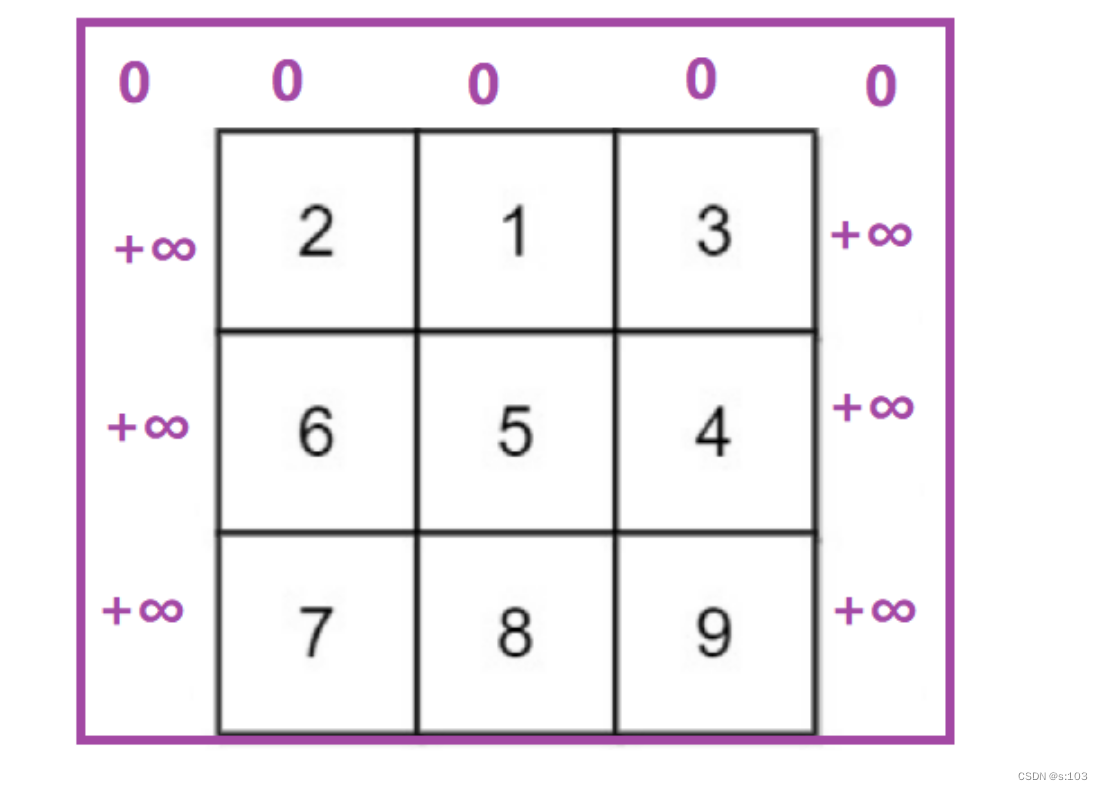
同样的,需要进行扩张矩阵,但是这次有边界问题的是这些:

所以要扩张这么一圈:
- 大小变为(m + 1) ×(n + 2)
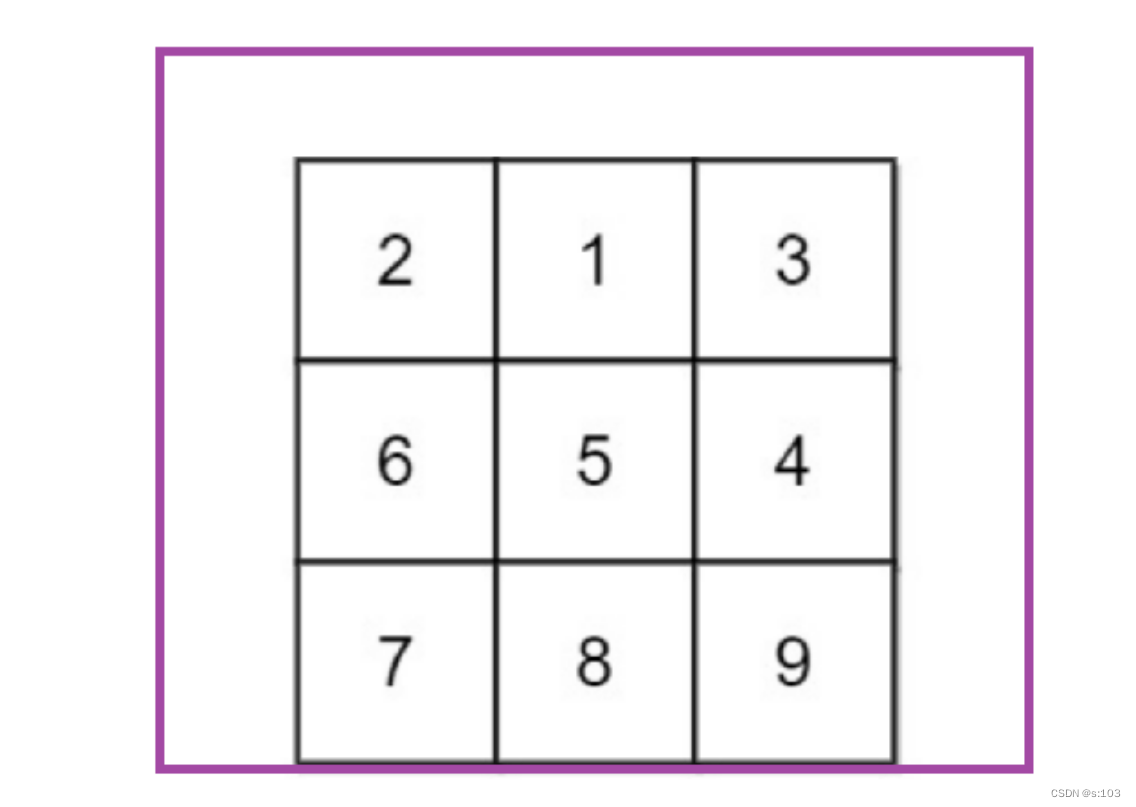
- 假数据不能影响真实值
- 用正无穷大避免假数据被选中为“较短路径”
- 下标对应问题
4.2.4 填表顺序
整体向下
4.2.5 返回值
由于扩张过矩阵,所以要注意下标的对应
应该返回最后一行中的“每个终点”,下降路径长最短的那种情况的值!
- 因为最后一行每个位置都可以是终点
4.3 编写代码
class Solution {
public int minFallingPathSum(int[][] matrix) {
//1. 创建dp表
//2. 初始化
//3. 填表
//4. 返回值
int m = matrix.length;
int n = matrix.length;
int[][] dp = new int[m + 1][n + 2];
for(int i = 1; i < m + 1; i++) {
dp[i][0] = Integer.MAX_VALUE;
dp[i][n + 1] = Integer.MAX_VALUE;
}
for(int i = 1; i < m + 1; i++) {
for(int j = 1; j < n + 1; j++) {
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i - 1][j - 1])
, dp[i - 1][j + 1]) + matrix[i - 1][j - 1];
}
}
int min = Integer.MAX_VALUE;
for(int i = 1; i < n + 1; i++) {
min = Math.min(min, dp[m][i]);
}
return min;
}
}

千万注意下标对应!
5. 最小路径和
传送门:力扣64
题目:
5.1 题目解析
- 本题与第三题“礼物的最大价值”极其相似,只是变成求最小值罢了~

5.2 算法原理
5.2.1 状态表示
我们需要通过经验 + 题目要求去决定状态表示:
- 根据题目的意境以及数据结构,我们得出需要建立二维dp表
- 经验:以某个坐标为结尾或者以某个坐标为起点去研究题目问题!
- 此题用的是“起点”
- 因为跟第三题差不多嘛,就换点花样去解题!
再根据经验,一般dp表的其中一值就应该是答案!
- 所以含义应该就是“路径最小权值和”
综合得到状态表示:dp[i][j]表示的就是(i, j)的位置**到达终点的路径最小权值和**
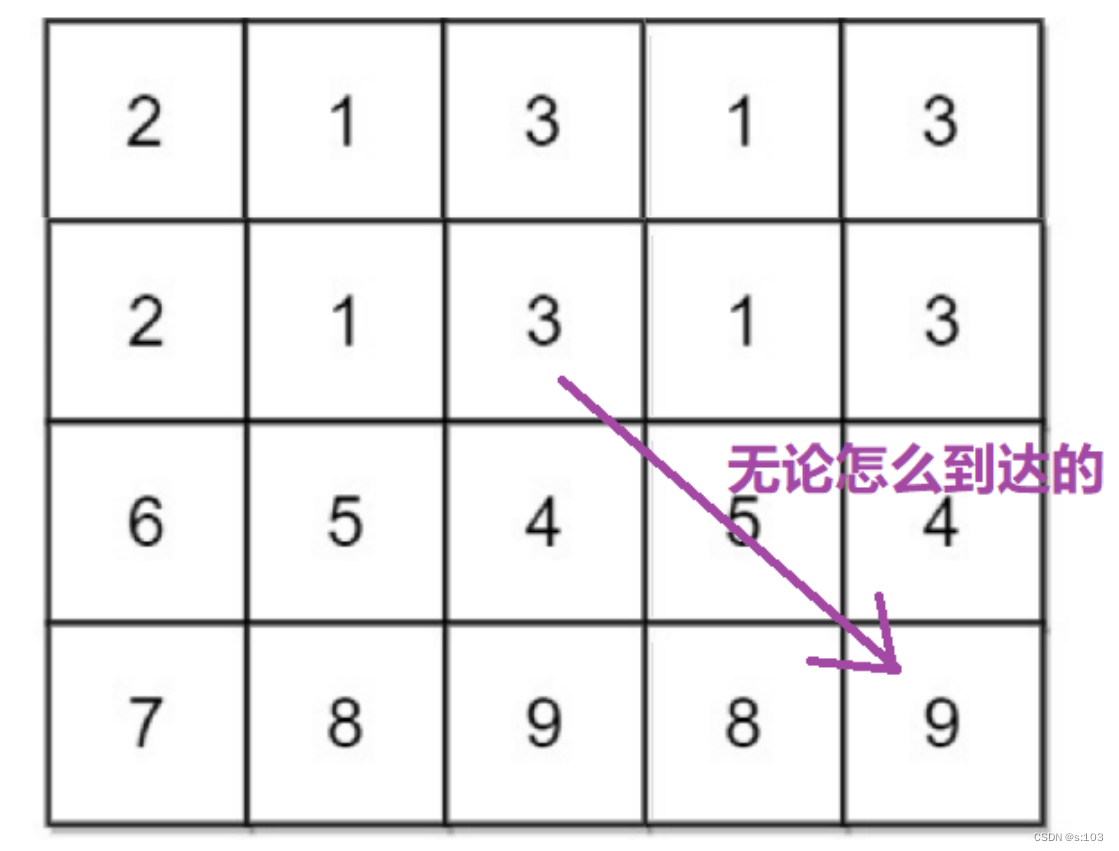
5.2.2 状态转移方程
同样的套路,我们需要根据已确定的dp表的值来推导dp[i] [j]的值,并且牢记dp表的状态表示!
- 我们以(i, j)为 起点
- 根据“最近一步”去划分问题
“最近一步”可以理解为“必然事件”
- 此题的“必然事件”就是,到达(i, j)之后要走的下一步,即(i + 1, j)或者(i, j + 1)
- 到达(i + 1, j)的话,(i + 1, j)到达终点的最小路径权值和 + grid[i] [j]
- 到达(i, j + 1)的话,(i, j + 1)到达终点的最小路径权值和 + grid[i] [j]
那么dp[i] [j]就是为这两种情况的较小值!
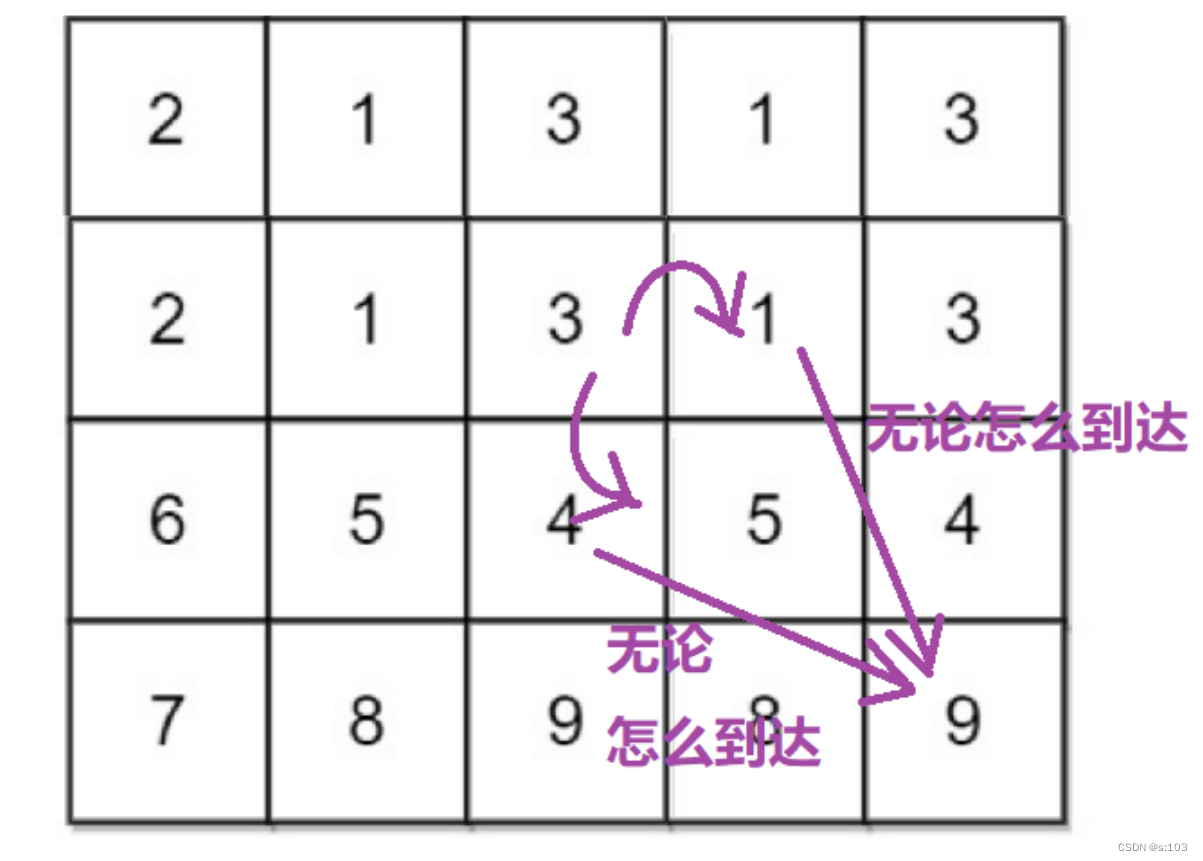
所以得出状态转移方程:
dp[i][j] = min{dp[i + 1][j], dp[i][j + 1]} + grid[i][j]
5.2.3 初始化
与“以某点为结尾”的方法不同的是,其面临边界的坐标不同:

所以扩张矩阵应该是这样的:
- 变成(m + 1) × (n + 1)
而我们要保证:
- 假数据不影响真实值
- 下标对应问题!
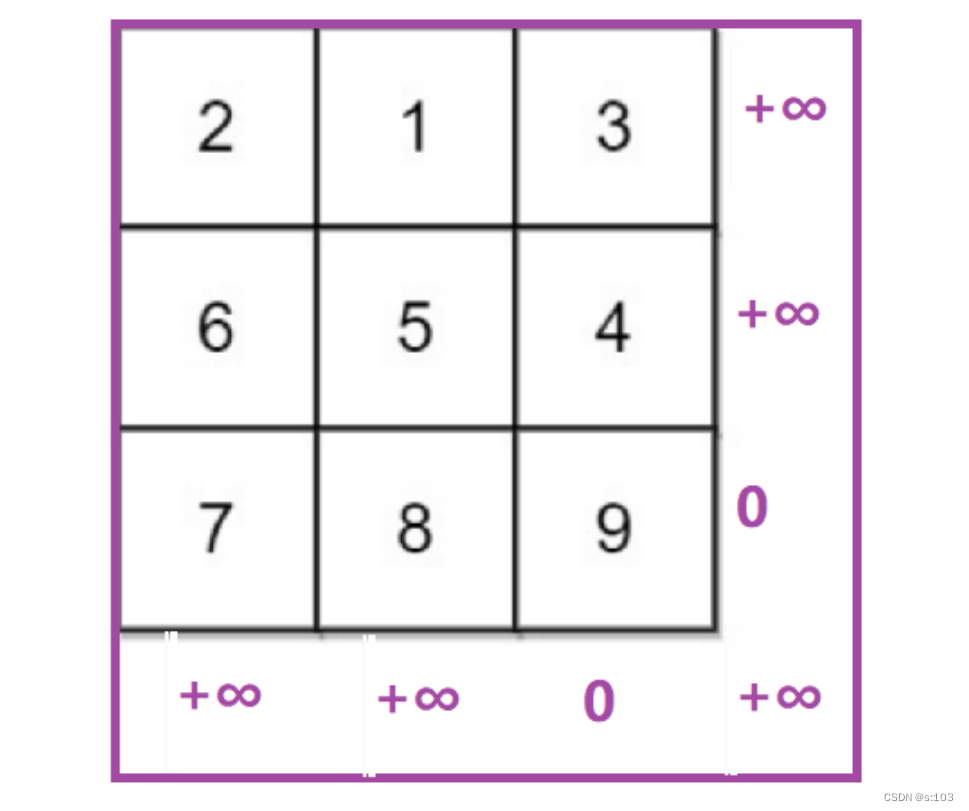
- 用无穷大防止被选中!
5.2.4 填表顺序
右下到左上:从下往上每一行,每一行从右到左
5.2.5 返回值
返回dp[0] [0],代表起点到终点的最小路径权值和
5.3 编写代码
class Solution {
public int minPathSum(int[][] grid) {
//1. 创建dp表
//2. 初始化
//3. 填表
//4. 返回值
int m = grid.length;
int n = grid[0].length;
int dp[][] = new int[m + 1][n + 1];
for(int i = 0; i < m + 1; i++) {
dp[i][n] = Integer.MAX_VALUE;
}
for(int j = 0; j < n + 1; j++) {
dp[m][j] = Integer.MAX_VALUE;
}
dp[m][n - 1] = 0;
dp[m - 1][n] = 0;
for(int i = m - 1; i >= 0; i--) {
for(int j = n - 1; j >= 0; j--) {
dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) + grid[i][j];
}
}
return dp[0][0];
}
}
本题下标对应没啥问题~
6. 地下城游戏
传送门:力扣174
题目:
6.1 题目解析

- 所以要杜绝一个思想:“寻找最小权值路径”,这肯定不是!
- 因为骑士中途会死亡!
- 这条路可能权值大于0,但是骑士也得保证在路上不能死亡!

6.2 算法原理
6.2.1 状态表示
我们需要通过经验 + 题目要求去决定状态表示:
- 根据题目的意境以及数据结构,我们得出需要建立二维dp表
- 经验:以某个坐标为结尾或者以某个坐标为起点去研究题目问题!
- 此题用的是“起点”
再根据经验,一般dp表的其中一值就应该是答案!
- 所以含义应该就是“最小初始血量”
综合得到状态表示:dp[i][j]的含义是,以此位置开始,到达公主返回需要的最少初始血量
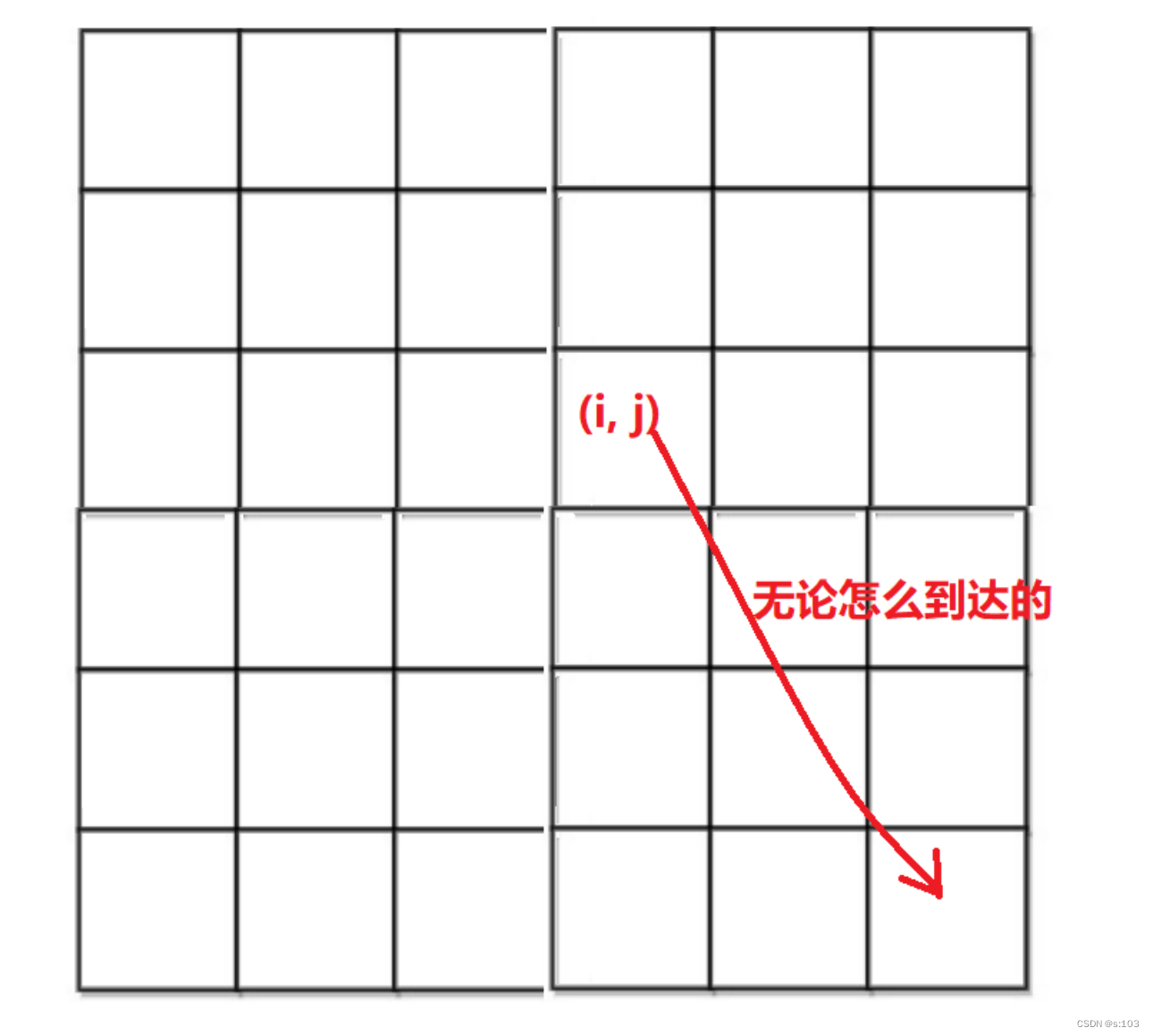
为什么不能“以某点为结尾”?
通过刚才的分析,明显在“正推”的过程中,时不时就要更新初始血量,及其难以用代码去实现(而这也是不应该出现在动态规划中的现象)
- 我们更希望,一个位置的血量能一次就确定下来
我们可以看出,如果是“以某点为终点”去研究,例如到达(0, 2)和(1, 2)时的dp值也没啥问题,但是这个方法并没有记忆当前回复的血量,所以会导致到达公主房间时得出的dp值偏高
- 而此时,我们是需要其后面节点的值去推导这个dp值,但是这并不能做到!
6.2.2 状态转移方程
同样的套路,我们需要根据已确定的dp表的值来推导dp[i] [j]的值,并且牢记dp表的状态表示!
- 我们以(i, j)为**起点**
- 根据“最近一步”去划分问题
“最近一步”可以理解为“必然事件”
- 此题的“必然事件”就是,到达(i, j)之后要走的下一步,即(i + 1, j)或者(i, j + 1)
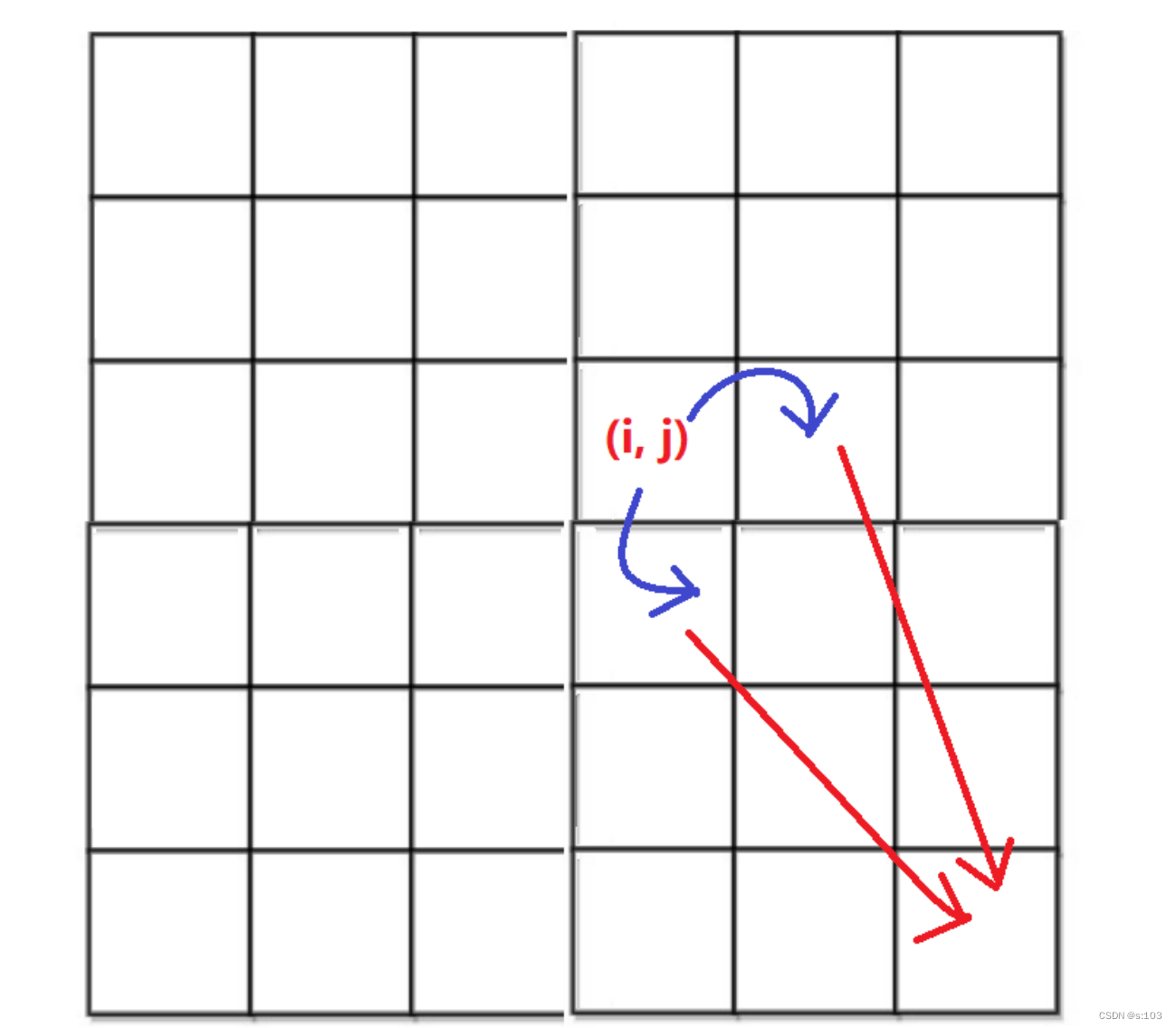
- 到达(i + 1, j)的话,要保证在(i, j)扣血或者回血后要能够由(i + 1, j)到达公主房间
- 即dp[i + 1] [j] - dungeon[i] [j]
- 到达(i, j + 1)的话,要保证在(i, j)扣血或者回血后要能够由(i, j + 1)到达公主房间
- 即dp[i] [j + 1] - dungeon[i] [j]
那么dp[i] [j]就是为这两种情况的较小值,当然dp[i] [j]必然 >= 1!
- 因为dungeon[i] [j]可能是回血包~
所以得出状态转移方程:
dp[i][j] = max{min{dp[i + 1][j], dp[i][j + 1]} - dungeon[i][j], 1}
6.2.3 初始化
同样的,应该扩张成这样:
- 根据映射表的大小推导出m和n,扩张后为(m + 1)×(n + 1)
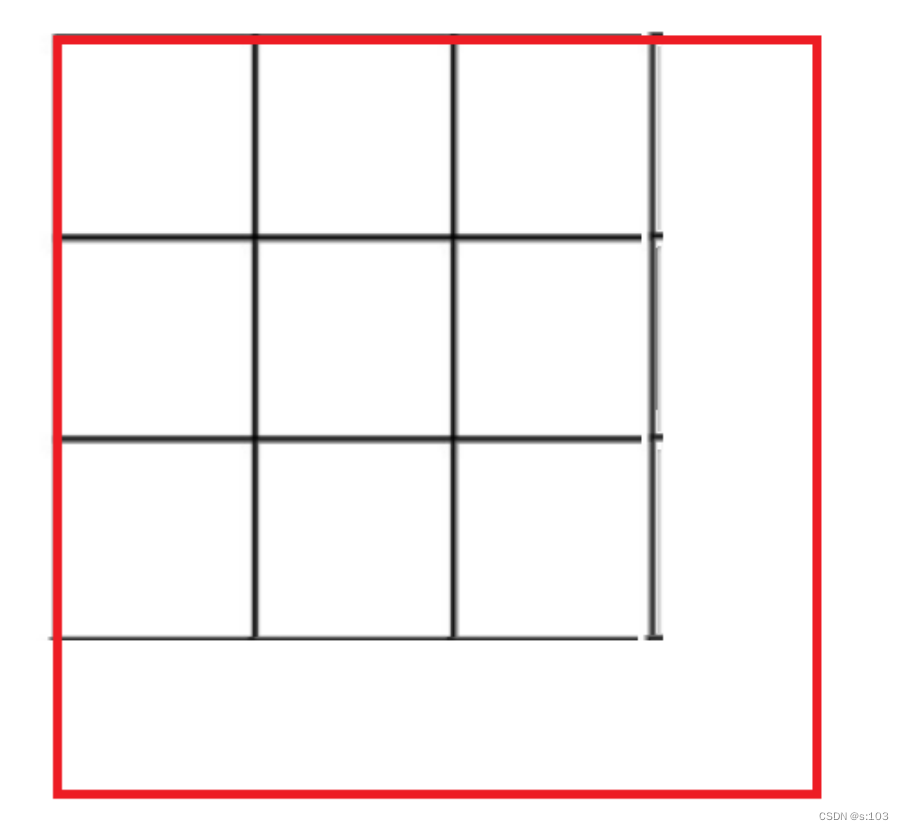
- 假数据不影响真实值
- 下标对应(这里无需考虑,因为并没有发生与映射表的下标位置的对应变化)
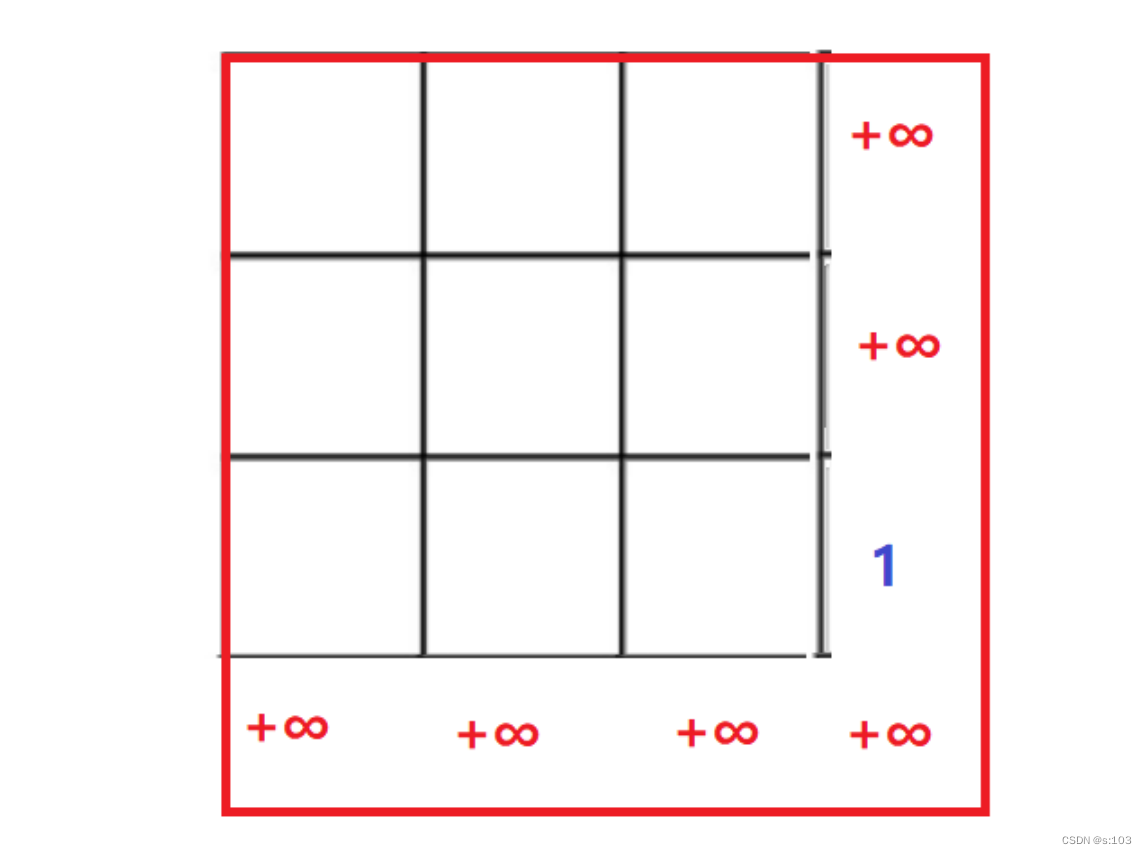
- 用无穷大防止被选中!
骑士到达公主房间,如果有扣血,则扣血后应该剩一滴血!
6.2.4 填表顺序
右下角到左上角:从下到上每一行,每一行从右到左
6.2.5 返回值
返回dp[0] [0],代表从起点到公主房间的最少初始血量
6.3 编写代码
class Solution {
public int calculateMinimumHP(int[][] dungeon) {
//1. 创建dp表
//2. 初始化
//3. 填表
//4. 返回值
int m = dungeon.length;
int n = dungeon[0].length;
int[][] dp = new int[m + 1][n + 1];
for(int i = 0; i < m + 1; i++) {
dp[i][n] = Integer.MAX_VALUE;
}
for(int j = 0; j < n + 1; j++) {
dp[m][j] = Integer.MAX_VALUE;
}
dp[m - 1][n] = 1;
for(int i = m - 1; i >= 0; i--) {
for(int j = n - 1; j >= 0; j--) {
dp[i][j] = Math.max(
1, Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]
);
}
}
return dp[0][0];
}
}
- 依靠算法原理照抄就行了~
文章到此结束!谢谢观看
可以叫我 小马,我可能写的不好或者有错误,但是一起加油鸭🦆!路径问题讲解完毕后,相信你对动态规划问题有了更好的理解,对整体流程也更加熟悉!
本文代码链接:动态规划02/src/Main.java · 游离态/马拉圈2023年6月 - 码云 - 开源中国 (gitee.com)