三维点云配准：理论、方法与挑战

注：”简要介绍“系列仅从概念上对某一领域进行非常简要的介绍，不适合用于深入和详细的了解

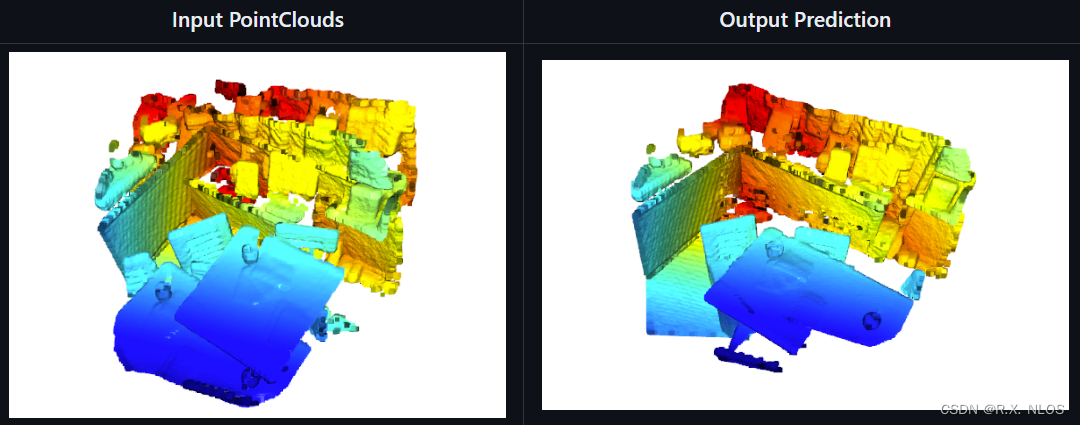
三维点云配准 是计算机视觉和机器人领域的重要课题，涉及从不同视角或时间点采集的三维点云数据之间寻找最佳对齐的过程。本文将详细介绍三维点云配准的背景、原理推导、研究现状、挑战以及未来展望。

1. 背景介绍

随着传感器技术的发展，三维点云数据在诸如 自动驾驶 、 遥感测绘 和 增强现实 等领域得到了广泛应用。要从这些数据中提取有用的信息，往往需要将多个点云融合为一个统一的坐标系。三维点云配准正是解决这一问题的关键技术。

2. 原理介绍和推导

2.1 配准问题的数学表示

给定两个点云 P = { p 1 , p 2 , … , p m } P=\{p_1, p_2, \dots, p_m\} P={p1​,p2​,…,pm​}和 Q = { q 1 , q 2 , … , q n } Q=\{q_1, q_2, \dots, q_n\} Q={q1​,q2​,…,qn​}，其中$p_i,q_j\in {\mathbb{R}}^3$。三维点云配准的目标是找到一个 刚体变换 （包括旋转矩阵$R$和平移向量$t$），使得$P$和$Q$之间的对齐误差最小。通常，我们使用 点对距离 作为误差度量：

$$E(R,t)=\sum _{i=1}^m\sum _{j=1}^n{w}_{ij}\Vert (R{p}_i+t)-q_j{\Vert }^2\text{\hspace{1em}(1)}$$

其中，$w_{ij}$表示点$p_i$和$q_j$之间的权重，反映了它们之间的相似性。

2.2 经典算法：Iterative Closest Point（ICP）

迭代最近点（ICP） 算法是最早提出的三维点云配准方法之一，其核心思想是在每次迭代中，寻找点云$P$中的每个点与点云$Q$中的最近邻点，并根据这些点对求解最优的刚体变换。ICP算法的基本步骤如下：

1. 初始化刚体变换$(R^{(0)},t^{(0)})$；
2. 在第$k$次迭代中，将点云$P$变换到点云$Q$的坐标系：$P^{(k)}=R^{(k-1)}P+t^{(k-1)}$；
3. 寻找点云$P^{(k)}$中的每个点与点云$Q$中的最近邻点；
4. 根据找到的点对，计算最优的刚体变换$(R^{(k)},t^{(k)})$；
5. 如果收敛，返回最终的刚体变换；否则，返回第2步。

ICP算法的关键步骤是计算最优的刚体变换。为了求解这一问题，我们可以使用 奇异值分解（SVD） 方法。具体来说，首先计算点对之间的 质心 ：

$${\mu }_P=\frac{1}{m}\sum _{i=1}^m{p}_i^{(k)},{\mu }_Q=\frac{1}{n}\sum _{j=1}^n{q}_j\text{\hspace{1em}(2)}$$

然后计算 协方差矩阵：

$$H=\sum _{i=1}^m(p_i^{(k)}-{\mu }_P)(q_i-{\mu }_Q{)}^T\text{\hspace{1em}(3)}$$

对$H$进行奇异值分解，得到$H=U\Sigma V^T$，则最优的旋转矩阵和平移向量为：

$$R^{(k)}=V{U}^T,t^{(k)}={\mu }_Q-R^{(k)}{\mu }_P\text{\hspace{1em}(4)}$$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SYFHHh1n-1686819349952)(https://example.com/ICP.jpg)]

2.3 基于特征的配准方法

除了ICP算法之外，还有许多基于 特征 的配准方法。这些方法首先在点云中提取有意义的特征，然后通过特征匹配来寻找点对。基于特征的方法通常具有较好的 鲁棒性 和 计算效率 ，但可能受到特征提取和匹配的误差影响。

3. 研究现状

近年来，基于深度学习的方法在点云配准领域取得了显著的成果。这些方法主要包括 监督学习方法 和 无监督学习方法 。

2.2.1 监督学习方法

监督学习方法通过训练神经网络来学习点云之间的局部或全局特征。常见思路包括

• 将输入点云通过多层感知器（MLP）进行特征提取，并采用最大池化层来获得全局特征。最后，通过解码器将全局特征映射到欧氏变换矩阵。

• 通过学习一个深度神经网络，将源点云和目标点云的局部特征映射到公共的描述空间，然后通过最小化描述子之间的距离来计算最优的变换矩阵。

2.2.2 无监督学习方法

无监督学习方法在点云配准中的应用相对较新，但已经取得了一定的效果。常见思路包括：

• 通过迭代地优化一个深度神经网络来学习源点云和目标点云的局部特征。首先将输入点云转换为图结构，然后使用图卷积神经网络（Graph Convolutional Networks, GCN）进行特征提取。接着，通过最大图匹配算法来寻找最佳的点对应关系，并计算最优的变换矩阵。

• 通过学习一个深度神经网络来预测点云之间的刚性变换。首先，使用基于卷积神经网络（CNN）的特征提取器从输入点云中提取局部特征。然后，通过全局优化算法（如RANSAC或分支定界）寻找最佳的变换矩阵。

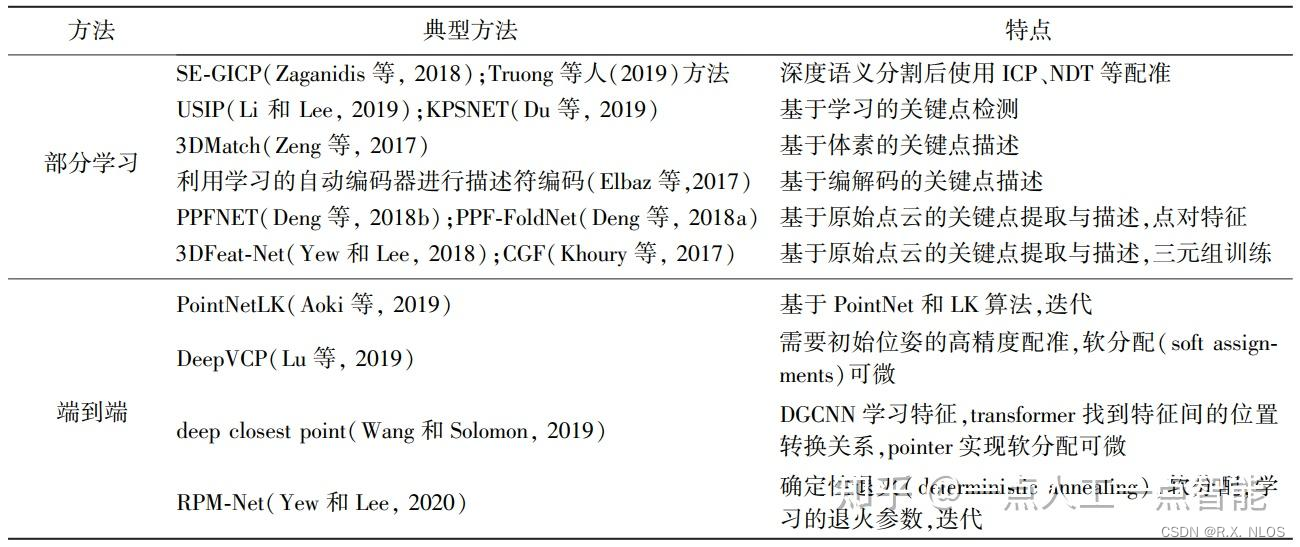
基于学习点云配准可参考：https://zhuanlan.zhihu.com/p/501503130

3. 挑战

尽管点云配准技术在过去的几年里取得了显著的进展，但仍然面临着一些挑战：

1. 噪声和异常值：点云数据通常含有噪声和异常值，这对于点云配准的精度和鲁棒性提出了挑战。研究人员需要设计更加鲁棒的算法来应对这一问题。

2. 部分重叠和遮挡：在实际应用中，源点云和目标点云之间往往存在部分重叠和遮挡的情况。这使得点云配准变得更加困难。未来的研究需要关注如何提高算法在这种情况下的性能。

3. 计算效率：尽管深度学习方法在点云配准的精度上取得了显著的提高，但它们通常需要较长的运行时间。为了满足实时应用的需求，未来的研究需要关注如何提高点云配准算法的计算效率。

4. 大规模点云数据：随着传感器技术的进步，我们可以获得越来越大规模的点云数据。处理这些大规模数据对于点云配准算法的计算效率和内存消耗提出了挑战。研究人员需要开发更加高效的算法来应对这一问题。

5. 多模态数据融合：在许多实际应用场景中，点云数据往往与其他类型的数据（如图像、激光雷达数据等）共同存在。如何有效地融合这些多模态数据以提高点云配准的性能是一个值得关注的研究方向。

4. 总结

本文回顾了点云配准的研究现状，介绍了主要的传统方法和基于深度学习的方法。尽管点云配准技术在过去的几年里取得了显著的进展，但仍然面临着诸如噪声和异常值、部分重叠和遮挡、计算效率等方面的挑战。未来的研究需要关注如何克服这些挑战，以满足实际应用中的需求。