文章目录
- Malthus模型问题
- 用最小儿二乘法估计阻滞增长模型
- 自来水运输问题
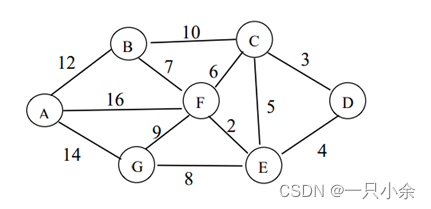
- 利用 Dijkstra 算法计算下图中起点 D 至各顶点得最短距离,需要给出
仅供参考
Malthus模型问题
1790-1980年间美国每隔10年的人口数量记录如下表所示。
表1 1790-1980年间美国每隔10年的人口数量记录表
| 年份 | 1790 | 1800 | 1810 | 1820 | 1830 | 1840 | 1850 | 1860 | 1870 | 1880 | 1890 | 1900 | 1910 | 1920 | 1930 | 1940 | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 人口 ( × 1 0 6 ) \left (\times 10^{6} \right ) (×106) | 3.9 | 5.3 | 7.2 | 9.6 | 12.9 | 17.1 | 23.2 | 31.4 | 38.6 | 50.2 | 62.9 | 76.0 | 92.0 | 106.5 | 123.2 | 131.7 | 150.7 | 179.3 | 204.0 | 226.5 | 251.4 | 281.4 |
x = 0:1:20;
p = [3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4];
z = log(p);
a = polyfit(x,z,1);
z = exp(polyval(a,x));
plot(x,p,'x',x,z,'r')

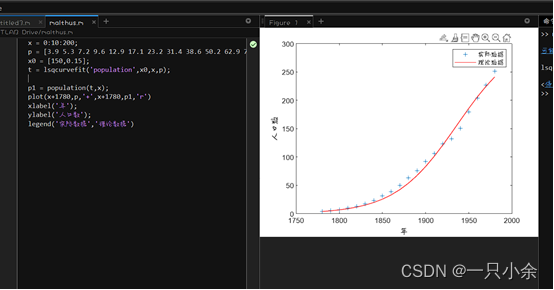
用最小儿二乘法估计阻滞增长模型
x = 0:10:200;
p = [3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4];
x0 = [150,0.15];
t = lsqcurvefit('population',x0,x,p);
p1 = population(t,x);
plot(x+1780,p,'+',x+1780,p1,'r')
xlabel('年');
ylabel('人口数');
legend('实际数据','理论数据')
function g = population(x,t)
g = x(1)./(1+(x(1)/3.9-1)*exp(-x(2)*t));
end
自来水运输问题
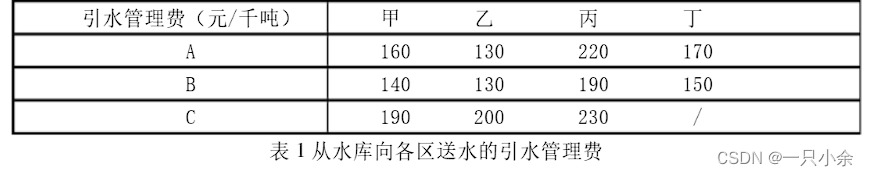
某市有甲,乙,丙,丁四个居民区,自来水有A,B,C三个水库供应。四个区每天必须得到保证的基本生活用水量分别是30,70,10,10千吨,但由于水源紧张,三个水库每天最多只能分别供应50,60,50千吨自来水。由于地理位置的差别,自来水公司从各水库向各区送水所需付出的引水管理费不同,其中水库与丁区之间没有输水管道),其他管理费用都是450元/千吨。根C据公司规定,各区用户按照统一标准900元/千吨收费。此外,四个区都向公司申请了额外用水量,分别为每天50,70,20,40千吨。该公司应如何分配供水量,才能获利最多?
为了增加供水量,自来水公司正在考虑进行水库改造,使三个水库每天的
最大供水量都提高一倍,问那时供水方案应如何改变?公司利润可增加到多少?
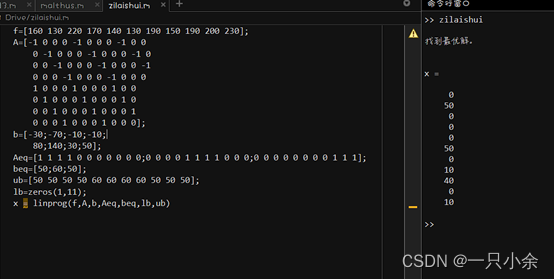
f=[160 130 220 170 140 130 190 150 190 200 230];
A=[-1 0 0 0 -1 0 0 0 -1 0 0
0 -1 0 0 0 -1 0 0 0 -1 0
0 0 -1 0 0 0 -1 0 0 0 -1
0 0 0 -1 0 0 0 -1 0 0 0
1 0 0 0 1 0 0 0 1 0 0
0 1 0 0 0 1 0 0 0 1 0
0 0 1 0 0 0 1 0 0 0 1
0 0 0 1 0 0 0 1 0 0 0];
b=[-30;-70;-10;-10;
80;140;30;50];
Aeq=[1 1 1 1 0 0 0 0 0 0 0;0 0 0 0 1 1 1 1 0 0 0;0 0 0 0 0 0 0 0 1 1 1];
beq=[50;60;50];
ub=[50 50 50 50 60 60 60 60 50 50 50];
lb=zeros(1,11);
x = linprog(f,A,b,Aeq,beq,lb,ub)
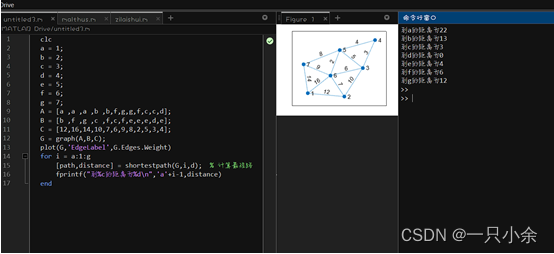
利用 Dijkstra 算法计算下图中起点 D 至各顶点得最短距离,需要给出
clc
a = 1;
b = 2;
c = 3;
d = 4;
e = 5;
f = 6;
g = 7;
A = [a ,a ,a ,b ,b,f,g,g,f,c,c,d];
B = [b ,f ,g ,c ,f,c,f,e,e,e,d,e];
C = [12,16,14,10,7,6,9,8,2,5,3,4];
G = graph(A,B,C);
plot(G,'EdgeLabel',G.Edges.Weight)
for i = a:1:g
[path,distance] = shortestpath(G,i,d); % 计算最短路
fprintf("到%c的距离为%d\n",'a'+i-1,distance)
end