文章目录
- LeetCode-4[题解] 寻找两个正序数组的中位数
- 问题描述
- 样例
- 解析
- 1 常规做法
- 2 二分+K-th Number解法
- 代码
LeetCode-4[题解] 寻找两个正序数组的中位数
问题描述
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
样例
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
解析
1 常规做法
常规做法很简单,虽然不满足题意,但是一定是最先想到的:
- 先归并排序在直接拎出中位数——时间复杂度 O ( m + n ) O(m+n) O(m+n),空间复杂度 O ( m + n ) O(m+n) O(m+n)
- 通过这两个数组可以知道整个数组的最小值/最大值,删除半个数组就可以找到中位数——时间复杂度 O ( m + n ) O(m+n) O(m+n),空间复杂度 O ( 1 ) O(1) O(1)
不满足题意的方法只能说是提供思路
2 二分+K-th Number解法
在题目要求时间复杂度在O(log (m+n)) 后,我们可以先整理出几个思路:
- 一定不能做任何遍历的操作:排序、移动指针。
- 我们已知的条件有什么?两个数组分别的最小值/最大值、综合后数组的最大值/最小值。
- 时间要求在log范围内,我自然就会想到二分。
在整理出这三点后我就陷入了误区,我一直想要用二分探索找到中位数的区间,但怎么都想不出来。~~通过大佬的一点小小启发,~~其实通过引入K-th Number的思想就可以解决这个问题。
- 思路:假如我们要在 m + n m+n m+n个数中找到中位数,等价于我们要找到第 K = ⌊ m + n + 1 2 ⌋ K = {\lfloor \frac{m+n+1}{2} \rfloor} K=⌊2m+n+1⌋小的数(如果是偶数只要再往后找一个就行)。
- 倘若我们要找到第 K K K个数,我们应该将前面的 K − 1 K-1 K−1个数全部去除。
为了保证时间复杂度合适,自然不能像常规第二种解法一样一个一个删除,而是使用二分的思想。但是这个二分有点难考虑到:通过比较两个数列中第 ⌊ K / 2 ⌋ {\lfloor K / 2 \rfloor} ⌊K/2⌋个数的大小,一定能删掉较小数列中的前 ⌊ K / 2 ⌋ {\lfloor K / 2 \rfloor} ⌊K/2⌋个数。为什么呢?下面我们分情况考虑一下:
-
若第K个数不在其中一个数列的前 ⌊ K / 2 ⌋ {\lfloor K / 2 \rfloor} ⌊K/2⌋个中:
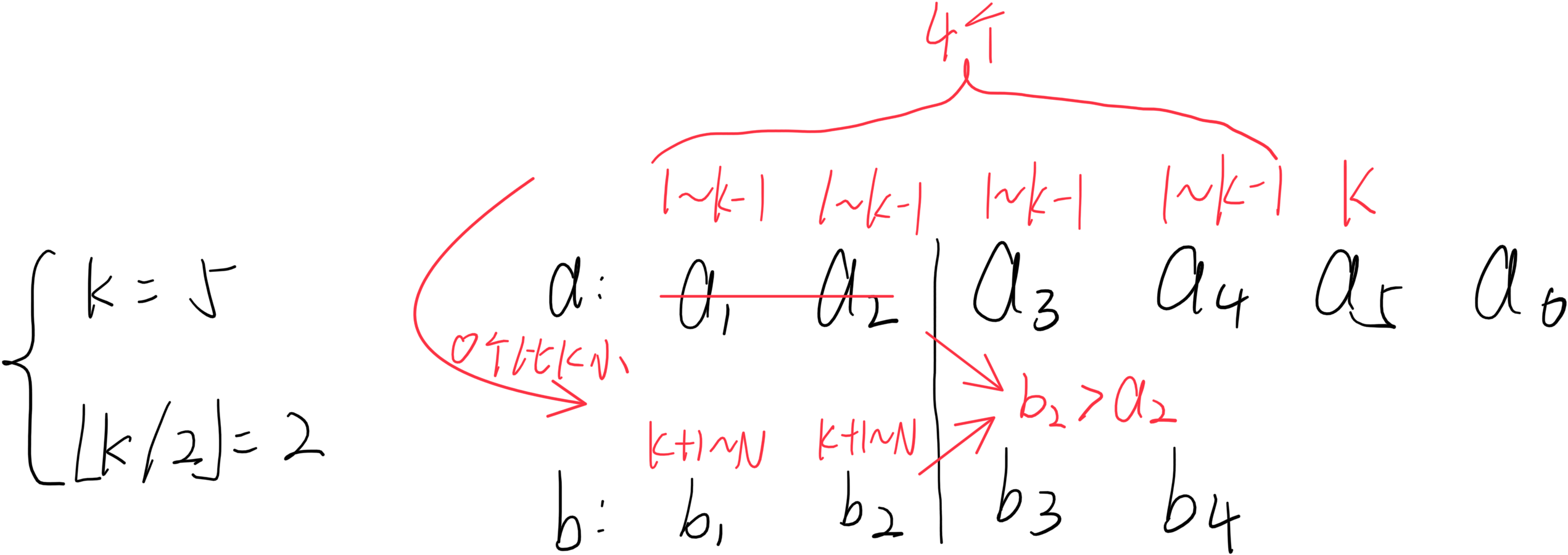
-
若在前 ⌊ K / 2 ⌋ {\lfloor K / 2 \rfloor} ⌊K/2⌋个中:
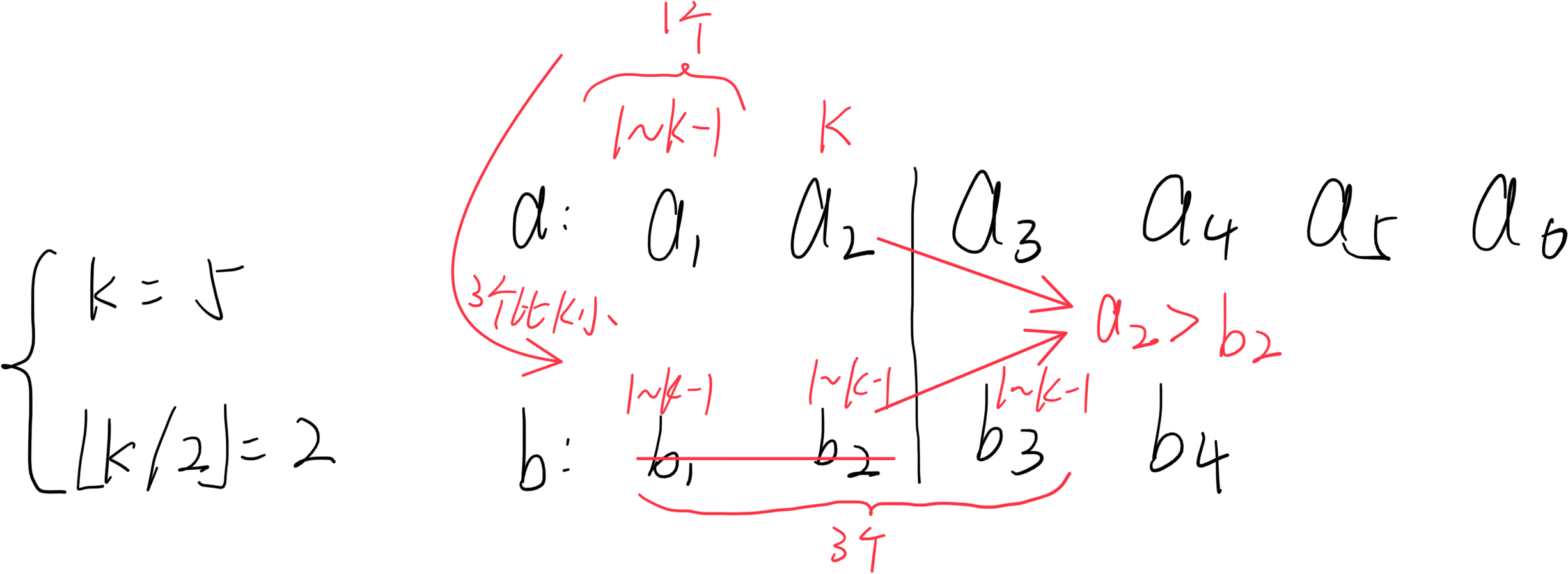
-
当然我们还要考虑一下特殊情况,超出范围则退到最远可比较的位置:
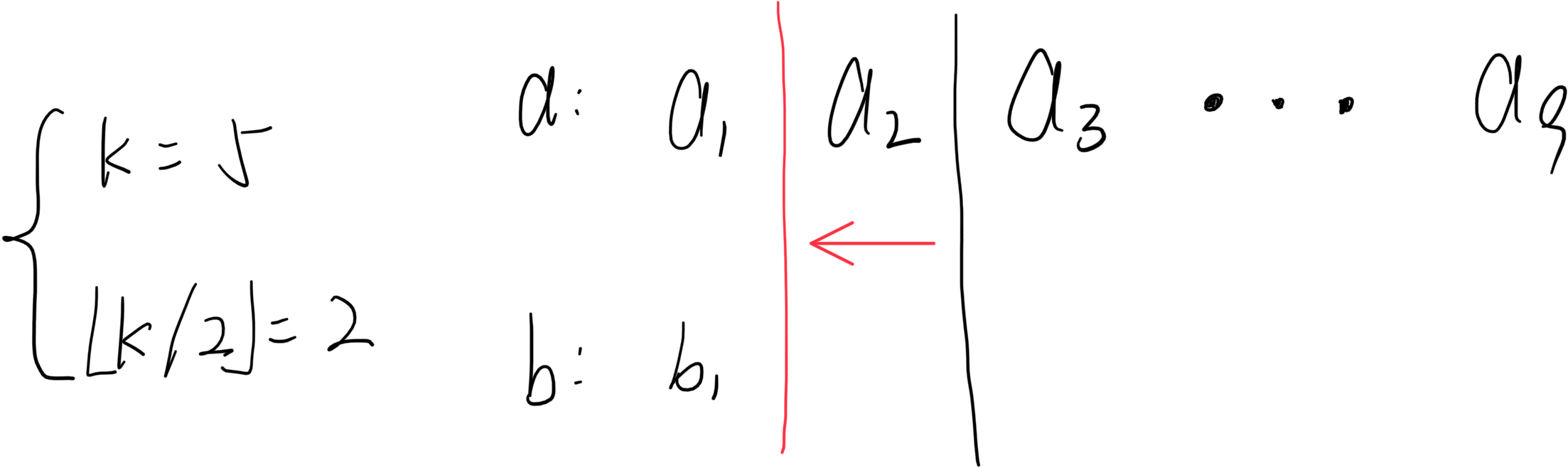
根据上述三种情况,我们一定在删除过程中不会删掉第 K K K个数。并且循环结束后我们可以将情况分成几种:
- 只剩一个数列:这个时候当前 K K K可能大于 1 1 1(由于好算,我们在代码直接判出),找到数列删掉的位置后面第 K K K个就好。
- 剩两个数列:这个时候 K K K一定等于 1 1 1(否则循环一定继续),找到当前两个数列的前两个数就好了(要注意考虑两个数组剩余数的个数,防止数组越界)。
这样就好啦,总结一下:
- 首先通过前 ⌊ K / 2 ⌋ {\lfloor K / 2 \rfloor} ⌊K/2⌋个数的理论,删除数组直到 K = 1 K=1 K=1或只剩一条数组。
- 然后分类讨论,若只有一条数组就找到目前第 K K K个数,两条数组就找到最小的两个数就好。
代码
总体来说不太优雅,因为最后讨论的情况比较多,别的大佬代码应该会好看许多
class Solution {
public:
pair<int, int> my_min(int a, int b1, int b2) {
if (a < b1) return {a, b1};
else return {b1, min(a, b2)};
}
pair<int, int> my_min(int a1, int a2, int b1, int b2) {
if (a1 < b1) return {a1, min(b1, min(a2, b2))};
else return {b1, min(a1, min(a2, b2))};
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int len1 = nums1.size(), len2 = nums2.size(); // 两个数组的长度
int k = (len1 + len2 + 1) / 2, odd = (len1 + len2) & 1; // 第k小数、奇偶性
int l1 = 0, l2 = 0; // 数组左端点
while (k > 1 && l1 < len1 && l2 < len2) {
int len = k / 2; // 探测的长度
// 一边超出限制
if (l1 + len > len1 || l2 + len > len2) len = min(len1 - l1, len2 - l2);
// 探测
if (nums1[l1 + len - 1] < nums2[l2 + len - 1]) l1 += len;
else l2 += len;
k -= len;
}
if (l1 == len1) return odd ? nums2[l2+k-1] : 1.0 * (nums2[l2+k-1] + nums2[l2+k]) / 2;
if (l2 == len2) return odd ? nums1[l1+k-1] : 1.0 * (nums1[l1+k-1] + nums1[l1+k]) / 2;
if (odd) return min(nums1[l1], nums2[l2]);
else if (len1 - l1 < 2 && len2 - l2 < 2) {
return 1.0 * (nums1[l1] + nums2[l2]) / 2;
} else if (len1 - l1 < 2) {
pair<int, int> mn = my_min(nums1[l1], nums2[l2], nums2[l2+1]);
return 1.0 * (mn.first + mn.second) / 2;
} else if (len2 - l2 < 2) {
pair<int, int> mn = my_min(nums2[l2], nums1[l1], nums1[l1+1]);
return 1.0 * (mn.first + mn.second) / 2;
} else {
pair<int, int> mn = my_min(nums1[l1], nums1[l1+1], nums2[l2], nums2[l2+1]);
return 1.0 * (mn.first + mn.second) / 2;
}
}
};