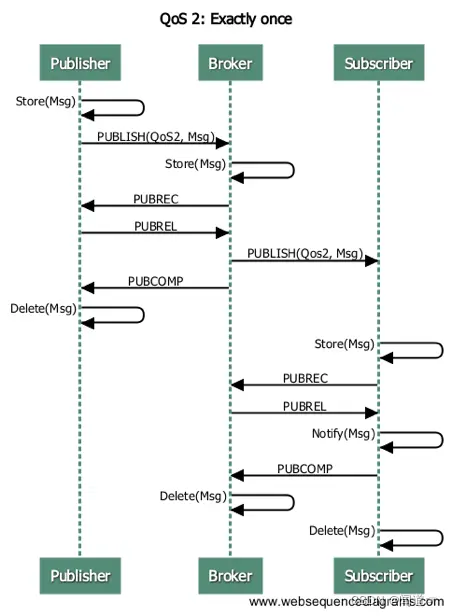
一、非对称加密简史

1、算法建立

        对于任何想发送加密信息的人，另一个问题是如何让接收人知道这条信息一开始是如何加密的。对于像字母替换式密码这样的密码，问题在于，一旦窃听者知道了加密方案，后续的信息都可以轻松获取。

        公钥加密(public-key encryption，简称PKE)系统可以解决这个问题。它使用了两个密钥，一个是公开的，另一个是保密的。两个密钥均由受信任的认证机构办法。公钥以电子证书的形式保存，任何想与其持有者进行通信的人都可以访问。

        公钥和私钥本质上都是数学上相关的多位数。这意味着二者任意之一都可以用来加密信息，只要解密它的时候使用的是另外一个密钥。

        20世纪70年代英国政府通信总部就开始了这项工作。与此同时，美国斯坦福大学的惠特菲尔迪・迪非和马丁・赫尔曼也独立构思出来，所以有时候这种算法也被成为迪非-赫尔曼加密。

        对于像破解的人来说，知道这两个密钥在数学上相关并没有太大帮助，从一个密钥推导另一个十分困难的。

        这种加密算法的优势之一是，不需要中央数据库来验证密钥，从而减少了密钥在验证过程中被窃听你的通信渠道的窃听者截获密钥。

2、应用于现实世界

        英国政府通信总部和斯坦福大学的研究工作为公钥加密奠定了基础，而麻省理工学院的三名研究人员罗纳德·李维斯特（Rona1d Rivest）、阿迪·沙米尔（AdiShamir）和伦纳德·阿德尔曼（Leonard Adleman）的突破性进展让它能够应用于实践。这三人发现了一种可以轻松地将公钥与私钥相关联的数学方法，而且它还能实现数字签名的交换,一种确认发送方身份的电子方法。他们的方法涉及因数和质数。

        对于任何给定数字，它的因数是指那些能够整除该数字（即不产生余数）的整数。例如，数字6的因数是1、2、3和6，因为6可以这些数字中的每一个整数而不产生余数。数字4不是6的因数，因为6除它本身和数以4，商为1，余数为2。质数是只有两个因数的数字，它本身和数字1。我们可以很明显地看出数字6不是质数，因为它有4个因数。相比之下，数字5仅能被自身和1整除，因此是质数。

        牢记这个定义，我们可以列出最前面的一批质数，2、3、5、7、13、17、19、23、29和31。数字1不被视为质数，因为它只有一个因数。将上述清单中最大的两个质数相乘，即29×31，是个很快的过程。在计算器上，这是一件微不足道的小事，只需几秒即可完成。你大概还能用铅笔和纸较快地完成这件事，甚至可以在不太长的时间内心算出结果，只要你选择捷径，先计算30×31，再减去31即可得到899这个数字。

        但是如果想反向解决这个问题，难度就大多了。如果给你899这个数字，并询问它的两个因数是什么，用计算器解决可能需要1个小时，用铅笔和纸需要1天，心算的话需要1周。

        随着质数变得更大，解决该问题所花费的时间会越来越长。2018年发现的最大的质数，其位数超过2400万。虽然这意味着将两个这样的数字相乘不是你的普通台式计算机能够做到的事情，但是只需少量的运算容量，你还是能够把它算出来。相反过程耗费的时间简直难以想象。然而，正如任何挑战一样，总是有人愿意尝试。最近破解232位密钥的一次成功尝试花费了相当于超过2000年的计算时间。

        质数的这种数学特性是李维斯特、沙米尔和阿德尔曼提出的办法的基础。三人成立的RSA安全公司估计，如今的应用软件一共使用了超过10亿份RSA加密标准。RSA的一种热门产品是名为SecurID的硬件令牌，它可以帮助识别想要远程访问公司IT系统的用户。用户使用虚拟专用网络（一种电子安全隧道）登陆他们的企业系统。每个用户都配备一个载有液品显示屏的钥匙扣状小型终端。显示屏上会出现一个6位数字，并且每60秒改变一次。要想访问系统，用户需要调用一个登录页面，并输人一个说明其身份的数字代码，加上当时显示在终端屏幕上的6位数字，然后输人预先设置的密码。他们所知道的东西（密码）和他们所拥有的东西（钥匙扣状终端）的这种结合正逐渐成为识别身份的常用方法。这种方法被通称为双因素身份认证(two-factor authentication)，很熟悉有没有，有些银行就会让我们花钱买这种东西，现在可能比较少了。

二、高级加密标准

        20世纪70年代中期，美国国家标准局(National Bureau of Standards，简称NBS)邀请有关方面就如何加密未经审查但敏感的政府数据提供想法。IBM计算机公司提出了使用一种对称分组加密算法（symmetric block cipher）的想法，这种密码用于固定长度的数据块，并使用相同的密钥进行加密和解密。也是很熟悉有没有，对称加密算法出现了。

        1977年，该密码的升级版本一一名为数据加密标准(Data Encryption Standard，简称DES)被迅速发布和采用。DES使用64位的数据块大小和同样大小的密钥，不过密钥中只有56位直接用于密码，其余部分用于减少传输过程中出错的可能性。RSA安全公司向能够破解DES密码的组织和个人悬赏，作为回应，电子前沿基金会（Electronic Frontier Foundation，简称EFF)专门建造了一台名为“深度解密"(Deep Crack）的机器，它可以使用暴力破解快速检查所有256种可能的密钥。1999年，EFF的演示表明它可以在不到一天的时间里完成这个过程。

        DES密码的一个升级版本一一一名为3DES(TripIed ES），在那一年被采用，但是随着计算机处理能力的增加，DES最终被证明是不安全的，并在2002年被高级加密标准(Advanced Encryption Standard，简称AES)取代。

        高级加密标准是两名比利时密码学家设计的，使用128位、192位或256位密钥（名为AES一128、AES一192、AES一256）加密长度为128位的数据块。这种加密涉及信息中移列和交换数位的各种循环，并且要对数位执行异或运算。

        目前从未出现让窃听者能够读取AES加密信息的公开已知攻击。话虽如此，但如今有很多已经发表的对AES的理论攻击，与完全的暴力破解攻击相比，它们能够以更快的速度解密信息。然而，完成这种攻击所需的时间实际上是不可行的。例如，在所谓的biclique攻击后面是数学图论的一个分支。人们在2011年发现这种攻击方法比暴力破解攻击快4倍。吹哨人爱德华．斯诺登(EdwardSnowden）的爆料表明，美国国家安全局曾经一直在寻找破解AES的新方法。

        由于用于公钥加密(PKE)的密钥极长，而且找到这些密钥所需的数学方法越来越复杂，现代密码破译如今基本上超出了感兴趣的业余爱好者的能力范围，而是数学家们的专门活动。但是，利用大数字因数分解的难度的加密系统中可能存在漏洞，这种诱人的可能性仍然存在。尽管到目前为止发现的因数分解方法在数学上都很复杂，但仍然可能存在某种更简单的方法。

三、打造安全的互联网

        虽然我们通过电子邮件发动的许多信息都是琐碎小事，但有时候我们还是想要确保没有人可以窥探到我们所说的话。例如，如果你在申请一份新工作，那么你最不想发生的事情就是你的现雇主发现这件事。

        加密电子邮件的一种方式是使用名为“优良保密协议"（Pretty Good Privacy，PGP）的软件包，它结合了传统密码体系和公钥加密的元素。PGP由菲利普，R.齐默尔曼创造，并于1991年
免费发布。PGP软件根据你的鼠标移动和键入方式生成随机密钥。然后这种随机密钥用于加密你的消息。

        在之后的发展阶段是使用公钥加密，但是用公钥加密的不是信息本身，而是上一阶段使用的随机密钥，然后将公钥加密后的随机密钥与使用随机密钥加密过的信息一起发送。当收件人收到你的消息时，他们不会用私钥解密信息，而是先解密随机密钥，然后用它解密附带信息。

        当你访问“https"网站时也会使用加密。可以通过浏览器窗口中出现的小挂锁标识来识别这种网站，而且它们的网址开头是https而不是http这样的网站使用的是名为传输层安全协议（security，简称TLS)的技术以及它的上一代技术安全套接层（secure sockets Layer，简称SSL)实际上，TLS和SSL使用如前所述的公钥加密来保护你和你与之对话的计算机之间的连接。例如'想要侵人你的银行账户详细信息的密码破译者，与试图破解使用相同加密方案发送的信息的密码破译者一样，都面临着同样的挑战。

四、公钥加密的数学示例

        下面是公钥加密一个简化的示例，首先选择两个质数P和Q。为了便于说明，P取11，Q为17。首先令P与Q相乘，得到181。这个数字称为模数（modulus）。然后我们在1和模数之间选择一个随机数字，该数字称为E，在这个例子里它是3。

        接下来，我们需要找到任意数字E，可被整除。在本例中，。320可以被160整除，于是我们可以找到这样一个D值：

        如果，因为我们已经选择E为3，那么D=107

        在这个非常简化的例子中，D的值是一个整数，使得计算尽可能容易。需要注意的是，这并不是唯一可能的值，因为我们可以选择某个不同的E值，或者选择使用480或640或者无数其它数字代替320。

        虽然看上去像是某种数学换算的小把戏，但是除非你知道P和Q各自的值，否则几乎无法根据E计算D的值，反之亦然。 

        现在让我们返回到公钥和私钥的问题上。我们与每个人分享的公钥实际上是两个数字模数（P×Q）和数字E，在我们的例子里就是181和3。私钥是数字D，在我们的例子里是107。

        我们不想泄露P和0各自的值，却将模数(PXQ)告诉所有人，这看似令人吃惊，但其实是这种技术的核心所在。如果P和Q的值足够大，通过对模数进行因式分解将它们找出需要花费的时间几乎是等于坐飞船飞到宇宙尽头一样。

        然后我们使用这些密钥对信息中的字符进行加密和解密。让我们对字母表中的字母进行编号。令A=1，z=26。要加密任何特定字符，我们会对它进行更多计算。假设我们要加密字母G，第7个字母，于是我们会从数字7开始。

        首先，我们计算7的E次幂。将同一个数字相乘E次，所以7的2次幂是7×7=49，等于7的平方；7的3次幂是7×7×7=343，等于7的立方。

        然后，我们使用一种名为模运算（modular arithmetic）的方法，这意味着你在达到一个固定值（称为模数）之后就会绕回来。模运算的一个很好的例子是看时间，它实际上是基于模数12的模运算（例如，10点再过5个小时不是15点，而是3点，因为抵达12点时，你会将时间重置到零）。

        我们已经计算出了模数P×Q的值，即181。数字343在使用模数181的模运算中等于162。这个数字就是我们的字母G加密后的形式。

        于是，我们将数字162和我们的私钥D（在本例中为107）发送给接收人，后者将执行类似的操作以解密信息。接收人计算162的107次幂，再次使用同样的模运算。可以想象，用162乘107次会得到一个绝对巨大的数字。实际上，它近似2后面加236个零。但是我们使用了模运算，如果我们每次到181时都将总数重置为零，最后会得到数字7。解密后的字符是7，也就是字母G。于是我们的接收人收到了信息的第一个字母，而我们可以按照相同的方式继续，直到整条信息都被秘密发送。

        如上，就连这个大大简化的例子也难以捉摸，而且它当然需要一台强大的计算机完成数学运算。如果我们使用了现代加密软件使用的那类数字，那么如果不用上一些世上最强大的计算机，就不可能完成相应的数学运算。