【LeetCode热题100】打卡第22天：编辑距离&颜色分类

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

编辑距离

🔒题目

原题链接：72.编辑距离（二刷了(●ˇ∀ˇ●)）

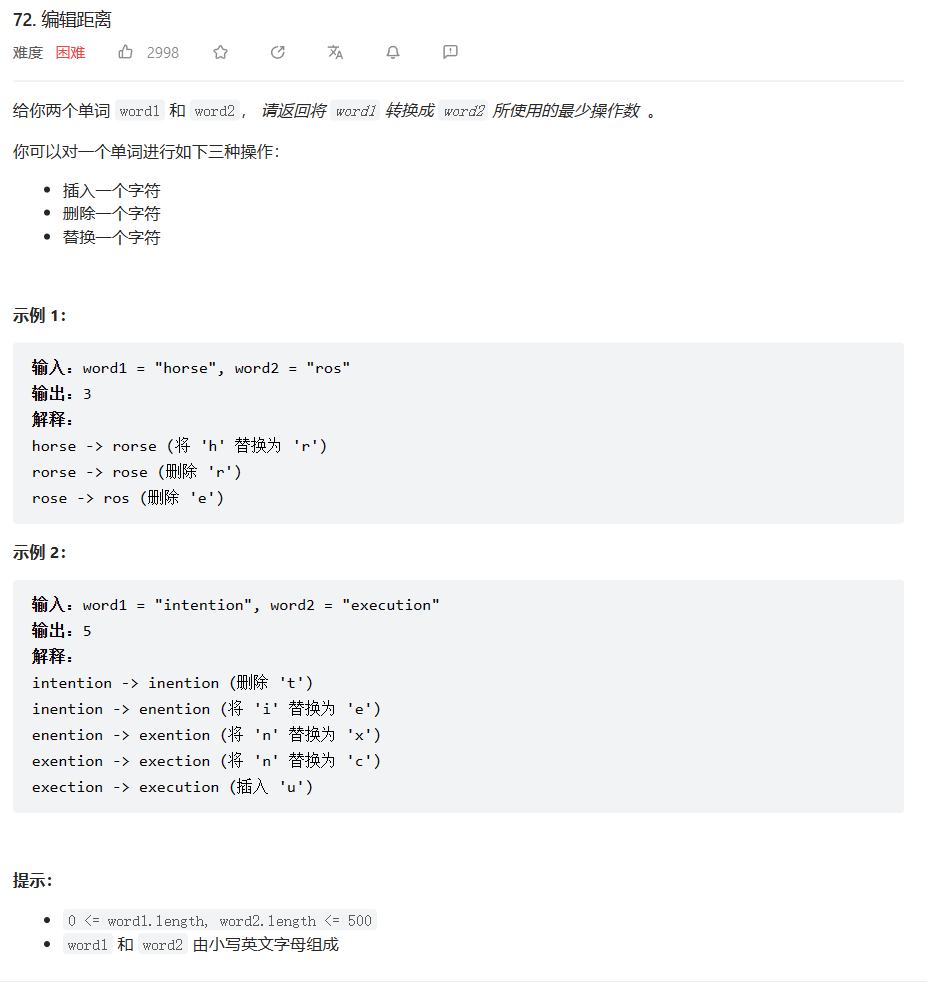
🔑题解

解法一：暴力DFS（时间超限）

直接暴力DFS相当于是进行了三层for循环，枚举出每一种操作的组合，时间复杂度相当高

/**
 * @author ghp
 * @title
 */

class Solution {

    public int minDistance(String word1, String word2) {
        return dfs(word1, word2, 0, 0);
    }

    public int dfs(String word1, String word2, int i, int j) {
        if (i == word1.length()) {
            // word1已经遍历完了
            return word2.length() - j;
        }
        if (j == word2.length()) {
            // word2已经遍历完了
            return word1.length() - i;
        }
        int res = 0;
        if (word1.charAt(i) == word2.charAt(j)) {
            // 当前两个字符相同，比较下一个字符
            res = dfs(word1, word2, i + 1, j + 1);
        } else {
            // 删除word1[i]，相当于在word2的j位置插入word1[i]
            int r1 = dfs(word1, word2, i + 1, j);
            // 替换word1[i]为word2[j]，相当于替换word2[j]为word1[i]，相当于同时删除word1[i]和word2[j]
            int r2 = dfs(word1, word2, i + 1, j + 1);
            // 删除word2[j]，相当于在word1的i位置插入word2[j]
            int r3 = dfs(word1, word2, i, j + 1);
            // 获取本次最小操作的次数
            res = 1 + Math.min(r1, Math.min(r2, r3));
        }
        return res;
    }
}

复杂度分析：

时间复杂度： $O(3^{m+n})$
空间复杂度： $O (m + n)$

其中 $n$ 为word1的长度， $m$ 为word2的长度

代码优化：DFS+记忆搜搜

直接使用DFS一般都是会超时，所以我们需要使用记忆搜索对搜索树进行剪枝，这样就能加快搜索效率，节约搜索时间

import java.util.Arrays;

/**
 * @author ghp
 * @title
 */

class Solution {

    private int[][] memo;

    public int minDistance(String word1, String word2) {
        memo = new int[word1.length()][word2.length()];
        for (int i = 0; i < memo.length; i++) {
            Arrays.fill(memo[i], -1);
        }
        return dfs(word1, word2, 0, 0);
    }

    public int dfs(String word1, String word2, int i, int j) {
        if (i == word1.length()) {
            // word1已经遍历完了
            return word2.length() - j;
        }
        if (j == word2.length()) {
            // word2已经遍历完了
            return word1.length() - i;
        }
        if (memo[i][j] != -1) {
            // 当前路径已被搜索
            return memo[i][j];
        }
        int res = 0;
        if (word1.charAt(i) == word2.charAt(j)) {
            // 当前两个字符相同，比较下一个字符
            res = dfs(word1, word2, i + 1, j + 1);
        } else {
            // 删除word1[i]，相当于在word2的j位置插入word1[i]
            int r1 = dfs(word1, word2, i + 1, j);
            // 替换word1[i]为word2[j]，相当于替换word2[j]为word1[i]，相当于同时删除word1[i]和word2[j]
            int r2 = dfs(word1, word2, i + 1, j + 1);
            // 删除word2[j]，相当于在word1的i位置插入word2[j]
            int r3 = dfs(word1, word2, i, j + 1);
            // 获取本次最小操作的次数
            res = 1 + Math.min(r1, Math.min(r2, r3));
        }
        memo[i][j] = res;
        return res;
    }
}

复杂度分析：

时间复杂度： $O (m * n)$
空间复杂度： $O (m * n)$

其中 $n$ 为word1的长度， $m$ 为word2的长度

解法二：动态规划

可能时间复杂度到 $O (n * m)$ ，已经是极限了，但是由于DFS需要递归，而每次递归都需要占用大量的栈内存，所以这里我们可以使用迭代替代递归，节约递归所消耗的栈内存，所以这题毫无疑问最优解就是动态规划，其实动规做得多的，一看这题就知道这是用过经典的动态规划问题，这一点从官方题解也可以看出，LeetCode官方也只提供了动态规划的题解。

但需要注意的是，并不是所有的题目，动态规划要优于DFS+记忆搜索，在非极值问题上，就不一定，比如在子问题数量超多，而DFS可以进行高效剪枝的情况下，DFS+memo的效率会优于DP算法，比如这道题【403.青蛙过河】

状态转移方程最难的就是状态转移方程以及DP的定义，这里大致给出一个思路：
- Step1：定义DP
  
  dp[i][j]表示word1中前i给字符，变换成word2中前j个字符，最短需要的操作数。由于wold1或world2中可能存在一个字母都没有的情况，即全增/删的情况，所以需要预留dp[0][j]和dp[i][0]，方便进行状态转移
- Step2：构造状态转移方程
  
  ①第一种情况：如果word1[i]（word1的第i个单词）和word2[j]）（word2的第j个单词）相同，则可以直接比较下一个，当前状态没有发生改变，也就是说当前的状态就是word1[i-1]和word2[j-1]的状态，所以状态方程是 $d p [i] [j] = d p [i - 1] [j - 1]$ ；
  
  ②第二种情况：如果word[i]不等于word2[j]，则需要进行三种操作，增、删、改，但是我们只需要选取三种操作中操作次数最小的一种即可。其中：
  
  增： $d p [i] [j] = d p [i] [j - 1] + 1$ ，dp[i][j-1]表示word1前i个字母于word2前j+1个字母进行匹配的最小操作数，相当于是在word2的第 j 个单词前添加一个word1[i]，是word[i]与word[j]匹配，然后当前操作数需要+1
  
  删： $d p [i] [j] = d p [i - 1] [j] + 1$ ，和增同理
  
  改： $d p [i] [j] = d p [i - 1] [j - 1] + 1$ ，和增同理
  
  当然，每次状态转移，我们都需要选取当前操作次数最小的一种，也就是有： $d p [i] [j] = 1 + M a t h . min (d p [i - 1] [j], M a t h . min (d p [i] [j - 1], d p [i - 1] [j - 1]))$
初始化DP（这里word1是horse，word2是ros）：

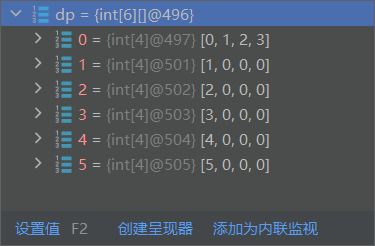
经过状态转移后的DP：
```
/**
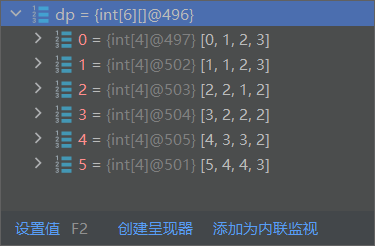
 * @author ghp
 * @title
 */

class Solution {

    public int minDistance(String word1, String word2) {
        int m = word1.length(), n = word2.length();
        int[][] dp = new int[m + 1][n + 1];
        // 初始化DP
        for (int i = 1; i <= m; i++) {
            dp[i][0] = i;
        }
        for (int j = 1; j <= n; j++) {
            dp[0][j] = j;
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = 1 + Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1]));
                }
            }
        }
        return dp[m][n];
    }
}
```
复杂度分析：
- 时间复杂度： $O (n * m)$
- 空间复杂度： $O (n * m)$
其中 $n$ 为word1的长度， $m$ 为word2的长度

代码优化：将二维DP压缩成一维DP

最后，我们还可以进一步优化空间，因为dp[i][j]的值只与它的邻居dp[i-1][j]、dp[i][j-1]、dp[i-1][j-1]有关，将二维数组压缩为一维数组，可以天然解决前两个依赖，问题就在于dp[i-1][j-1]的值如何保存，很显然，可以将这一维的数据压缩成一个值，于是，我们可以使用一个一维数组加一个变量来替换原来的二维数组
```
/**
 * @author ghp
 * @title
 */

class Solution {

    public int minDistance(String word1, String word2) {
        int m = word1.length(), n = word2.length();
        int[] dp = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            dp[i] = i;
        }
        for (int i = 1; i <= m; i++) {
            int pre = dp[0];
            dp[0] = i;
            for (int j = 1; j <= n; j++) {
                int temp = dp[j];
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[j] = pre;
                } else {
                    dp[j] = 1 + Math.min(dp[j-1], Math.min(dp[j], pre));
                }
                pre = temp;
            }
        }
        return dp[n];
    }
}
```

最后我们经过 $D FS \to D FS + 记忆搜索 \to 二维 D P \to 一维 D P$ 的层层优化，最终得到本题的最优解，也就是一维DP，但需要注意并不是说所有的可以使用动规和DFS的题，就一定是DP优于DFS，有些情况，题目的子问题过多可能就是DFS优于DP

PS：说句实话，我感觉DP还更加好理解一点，DFS+记忆搜索反而绕的有点晕，而且这里DP的效率是要高于DFS+记忆搜索的

颜色分类

🔒题目

原题链接：75.颜色分类

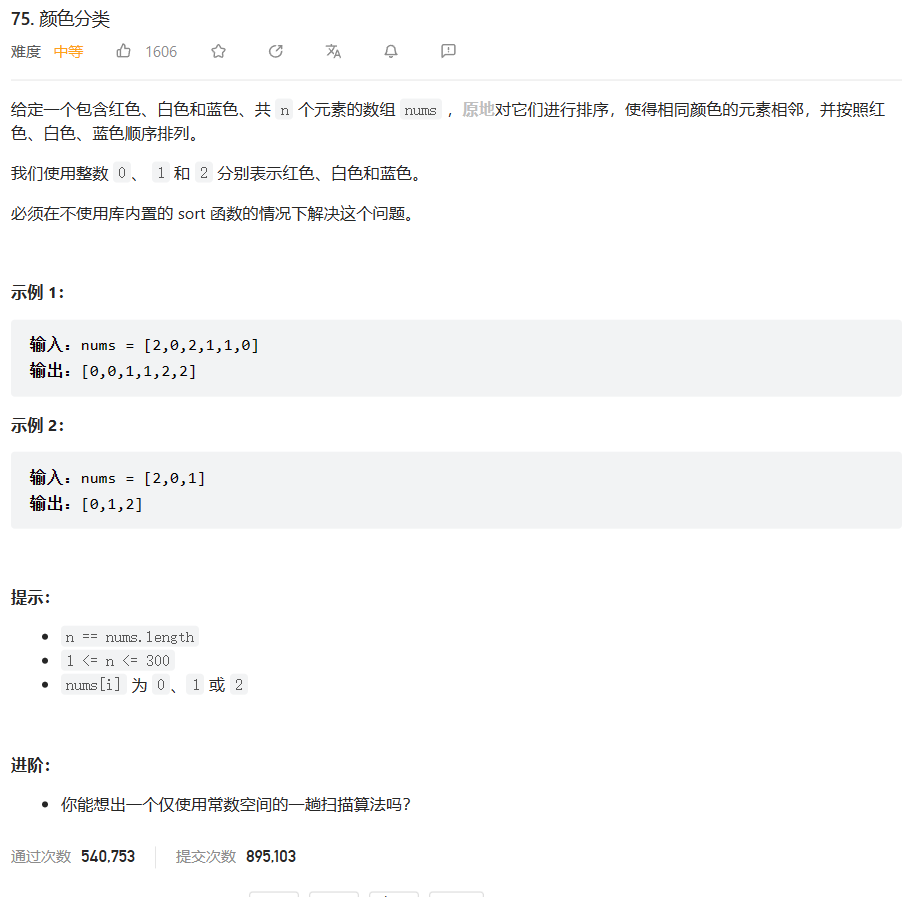
🔑题解

解法一：调用API

Arrays.sort是Java中用于排序的静态方法，它的时间复杂度为 $O (n l o g n)$ 。具体来说，它使用的是快速排序或Tim排序(Java 7及以上版本)。在空间复杂度方面，Arrays.sort属于“原地排序”，也就是说，它只使用了常数级别的额外空间，因此空间复杂度为 $O (1)$ 。需要注意的是，对于基本类型数组，Arrays.sort使用的是“双轴快速排序”，而对于对象数组，Arrays.sort使用的是“归并排序”。这可能会影响排序的性能和稳定性。同时，如果要对对象数组进行排序，并且排序字段可能有重复的值，那么建议使用Java 8及以上版本的Streams API中的sorted方法，它提供了更好的排序性能和稳定性。
```
import java.util.Arrays;

/**
 * @author ghp
 * @title
 */
class Solution {
    public void sortColors(int[] nums) {
        Arrays.sort(nums);
    }
}
```
复杂度分析：
- 时间复杂度： $O (n l o g n)$
- 空间复杂度： $O (1)$
其中 $n$ 为数组中元素的个数

解法二：快排

解法一的Arrays.sort底层也是快排算法，这里就手写一遍快排，就当作重新复习一遍吧O(∩_∩)O

/**
 * @author ghp
 * @title
 */
class Solution {
    public void sortColors(int[] nums) {
        quickSort(nums, 0, nums.length - 1);
    }

    private void quickSort(int[] nums, int l, int r) {
        if (l >= r) {
            return;
        }
        // 划分区间，同时获取主元索引
        int pivot = partition(nums, l, r);
        quickSort(nums, l, pivot - 1);
        quickSort(nums, pivot + 1, r);
    }

    private int partition(int[] nums, int l, int r) {
        int pivot = nums[r];
        int i = l - 1;
        int j = l;
        int temp;
        // 划分区间（左侧区间元素<主元，右侧区间元素>=主元）
        while (j < r) {
            if (nums[j] < pivot) {
                temp = nums[j];
                nums[j] = nums[i + 1];
                nums[i + 1] = temp;
                i++;
            }
            j++;
        }
        // 将主元放到分界点
        temp = nums[r];
        nums[r] = nums[i + 1];
        nums[i + 1] = temp;
        return i + 1;
    }
}

复杂度分析：

时间复杂度： $O (n l o g n)$
空间复杂度： $O (1)$

其中 $n$ 为数组中元素的个数

解法三：三路快排算法

上面的代码使用的是荷兰国旗问题的算法，也叫三路快排算法。该算法的思想源于快速排序，可以在 $O (n)$ 的时间复杂度内将一个数组分为三部分：小于某个数、等于某个数和大于某个数。

这应该是本体的最优解了！这方法实现起来也简单，也容易懂，就是很难想得到🤣
```
/**
 * @author ghp
 * @title
 */
class Solution {
    public void sortColors(int[] nums) {
        int i = 0;
        int j = 0;
        for (int k = 0; k < nums.length; k++) {
            int num = nums[k];
            nums[k] = 2;
            if (num < 2) {
                nums[j++] = 1;
            }
            if (num < 1) {
                nums[i++] = 0;
            }
        }
    }
}
```
复杂度分析：
- 时间复杂度： $O (n)$
- 空间复杂度： $O (1)$
其中 $n$ 为数组中元素的个数

解法四：三指针算法

/**
 * @author ghp
 * @title
 */
class Solution {
    public void sortColors(int[] nums) {
        int i = 0;
        int j = 0;
        int k = nums.length - 1;
        while (i <= k) {
            if (nums[i] == 0) {
                swap(nums, i++, j++);
            } else if (nums[i] == 2) {
                swap(nums, i, k--);
            } else {
                i++;
            }
        }
    }

    private void swap(int[] nums, int i, int j) {
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
}

解法五：归并排序

这种解法也能过，但是不符合题意，因为题目要求要原地排序，不能使用第三方数组。我写在这里，单纯是为了复习一遍归并排序算法

import java.util.Arrays;

/**
 * @author ghp
 * @title
 */

class Solution {
    public void sortColors(int[] nums) {
        divide(nums, 0, nums.length - 1);
        System.out.println(Arrays.toString(nums));
    }

    private void divide(int[] nums, int l, int r) {
        if (l >= r) {
            return;
        }
        int mid = (r - l) / 2 + l;
        divide(nums, l, mid);
        divide(nums, mid + 1, r);
        merge(nums, l, mid, r);
    }

    private void merge(int[] nums, int l, int mid, int r) {
        int i = l;
        int j = mid + 1;
        int k = 0;
        int[] temp = new int[r - l + 1];
        while (i <= mid && j <= r) {
            if (nums[i] < nums[j]) {
                temp[k++] = nums[i++];
            } else {
                temp[k++] = nums[j++];
            }
        }
        while (i <= mid) {
            temp[k++] = nums[i++];
        }
        while (j<=r){
            temp[k++] = nums[j++];
        }
        for (int m = 0; m < k; m++) {
            nums[l+m] = temp[m];
        }
    }
}