基本思路

此题为重点题目
此题实际上可以分为俩题：
1 判断是否存在环
2 如果存在返回环的入口 如果不存在返回null

那我就对于这俩种情况进行相关的解释。

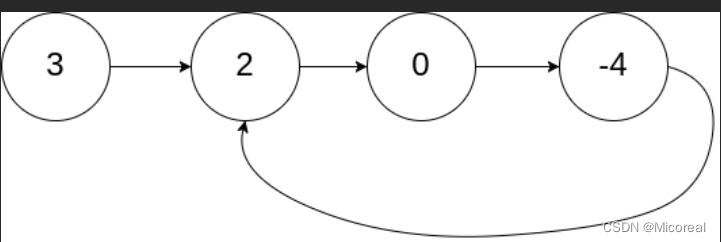
1. 判断是否有环
   有点类似追及问题，我们可以定义一个快指针，一个慢指针，都从初始的3开始行动快指针一次走俩步，慢指针一次走一步，最后只需要while判断是否存在一个节点让快慢指针相遇，即可判断此链表是否存在环（环链表尾部不会存在null的）。

2. 判断环的入口
   由于我们定义的快慢指针速度比为2:1，那么实际上路程比也是2：1。通过这一点我们可以列出一个方程式。这里假设从开头到环节点的距离是x（用于判断环节点的距离），从环节点到相遇点是y，从相遇点到环节点是z，那么对于慢节点来说，他s = x + y + n1（y+z）吗？我们可以进行分析，由于快指针的速度是慢指针的n倍，所以实际上在快指针走完第二圈的时候就肯定会追上慢指针，（拿极限情况进行分析：环节点就是头节点，刚好就是慢指针走完一圈，快指针走完俩圈），所以实际上慢节点s1= x + y，快节点的路程是s2 = x + y + z + y（多走一圈），而两者的路程比为2：1 由此可以得到等式:
   2(x+y) = x + y + z + y
   化简：x = z
   那么问题就简单了此时我们要求取环的入口只需要在相遇点以及头节点同时定义一个指针，进行遍历，二者何时相遇就是环节点了。

leetcode 142 环形链表

链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        //定义一组快慢节点
        ListNode* fast = head;
        ListNode* slow = head;
        //寻找相遇的节点位置，（此时关注如果没有环，实际上fast就会先走到null，所以可以进行判断,但是值得关注的问题是我们后续是会fast = fast->next->next,故如果仅仅是while(fast)会有很大的问题，问题就是我们仅仅判断了fast！=null 若fast->next = null,那么我们又取他的下一个节点就会有很大的问题了。）    
        while(fast && fast->next)
        {
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow)
            {
                //有环
                break;
            }
        }
        //如果此时无环就可以直接返回null了，有环才需要返回环头节点
        if(!fast || !fast->next)
            return NULL;
        else
        {
            //如果存在需要求出环节点
            ListNode* result = head;
            while(result != fast)
            {
                result = result->next;
                fast = fast->next;
            }
            return result;
        }


    }
};