1. 特征降维（PCA）

回顾知识点：

特征降维是指将高维特征空间的数据映射到低维空间的过程，以减少特征的数量并保留数据的主要信息。下面是特征降维的一般步骤：

（1）求特征协方差矩阵：对原始数据进行预处理，计算特征之间的协方差矩阵。协方差矩阵描述了特征之间的线性关系。

（2）求协方差的特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。

（3）排序选择特征：将特征值按照从大到小的顺序进行排序，选择其中最大的k个特征值对应的特征向量作为主要特征。

（4）样本投影：将原始数据样本点投影到选取的特征向量所张成的低维空间上，得到降维后的数据表示。

通过特征降维，可以减少数据的维度，降低计算复杂度，去除冗余信息，提取主要特征，从而更好地理解数据、可视化数据、加快模型训练和预测等。

需要注意的是，特征降维方法有多种，除了基于协方差矩阵的主成分分析（PCA）方法外，还有独立成分分析（ICA）、线性判别分析（LDA）等方法，选择合适的特征降维方法要根据具体任务和数据特点进行综合考虑。

2. LDA 降维

2.1 概述

LDA（Linear Discriminant Analysis）降维是一种经典的线性降维方法，其核心思想是通过投影变换将数据映射到一个低维空间，使得同一类别内的样本尽可能接近，不同类别之间的样本尽可能远离。

具体的步骤如下：

（1）计算类内散度矩阵（Within-class scatter matrix）：对于每个类别，计算该类别内样本的协方差矩阵，然后将所有类别的协方差矩阵求和，得到类内散度矩阵。

（2）计算类间散度矩阵（Between-class scatter matrix）：计算每个类别的均值向量，然后计算所有类别均值向量的协方差矩阵，得到类间散度矩阵。

（3）解决广义特征值问题：通过求解广义特征值问题，找到类内散度矩阵的逆矩阵与类间散度矩阵的乘积的特征向量和特征值。

（4）选择最大的k个特征值对应的特征向量：将特征值按照从大到小排序，选择最大的k个特征值对应的特征向量。

（5）投影数据：将原始数据样本点投影到选取的特征向量所张成的低维空间上，得到降维后的数据表示。

LDA降维方法的目标是在降低维度的同时，尽可能地保留类别间的差异性，提高分类性能。它在模式识别、人脸识别、图像处理等领域有广泛应用。

需要注意的是，LDA是一种有监督的降维方法，需要样本的标签信息来进行类别间的判别。

2.2 标注间距离的衡量

在LDA降维中，同一标注内距离的衡量通常使用类内散度矩阵（Within-class scatter matrix）来表示。类内散度矩阵衡量了同一类别内样本点之间的距离，希望同一类别内的样本点尽可能接近。类内散度矩阵可以通过计算每个类别内样本的协方差矩阵，并将所有类别的协方差矩阵求和得到。

而不同标注间距离的平衡通常使用类间散度矩阵（Between-class scatter matrix）来表示。类间散度矩阵衡量了不同类别之间的距离，希望不同类别之间的样本点尽可能远离。类间散度矩阵可以通过计算每个类别的均值向量，然后计算所有类别均值向量的协方差矩阵得到。

在LDA中，我们的目标是最大化类间散度矩阵与类内散度矩阵之间的比值，从而达到同一标注内距离尽可能小，不同标注间距离尽可能大的效果。这一比值被称为广义瑞利商（Generalized Rayleigh Quotient），我们通过求解广义特征值问题来得到最大化该比值的特征向量。

通过调整类内散度矩阵与类间散度矩阵之间的平衡，我们可以控制同一标注内距离和不同标注间距离的权重，以满足具体问题的需求。

最佳转换图：

2.3 python操作LDA

import numpy as np
import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# 创建特征矩阵X
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [3, 2]])
print(X)

# 创建标签数组Y
Y = np.array([1, 1, 1, 2, 2, 2])
print(Y)

# 使用LinearDiscriminantAnalysis进行特征降维
lda_result = LinearDiscriminantAnalysis(n_components=1).fit_transform(X, Y[:5])
print(lda_result)

# 创建LinearDiscriminantAnalysis分类器并拟合数据
clf = LinearDiscriminantAnalysis(n_components=1).fit(X, Y[:5])
print(clf)

# 预测新样本的标签
print(clf.predict([[0.8, 1]]))

执行结果如下：

[[-1 -1]
 [-2 -1]
 [-3 -2]
 [ 1  1]
 [ 3  2]]
[1 1 1 2 2 2]
[[-1.87888373]
 [-0.96974644]
 [-3.09106679]
 [ 2.36375695]
 [ 3.57594001]]
LinearDiscriminantAnalysis(n_components=1)
[2]

结果分析：

原始特征矩阵X包含了5个样本，每个样本有2个特征。
标签数组Y表示了对应于特征矩阵X中每个样本的类别标签。
经过LDA降维后，特征矩阵X从2维降至1维，得到降维后的结果lda_result。
创建的LinearDiscriminantAnalysis分类器对象clf通过拟合特征矩阵X和标签数组Y[:5]得到。
对新样本[[0.8, 1]]进行预测，分类器预测其标签为2。

3. 特征衍生

3.1 概述

特征衍生是指根据已有的特征或属性，通过变换、组合或生成新的特征来丰富数据集的过程。特征衍生的目的是通过创造新的特征，提取数据中的隐藏信息、增加模型的表达能力、改善模型的性能等。

特征衍生的方法可以包括以下几种：

（1）算术运算：通过对现有特征进行加减乘除等算术运算，生成新的特征。例如，将身高和体重结合计算BMI指数。

（2）多项式特征：通过对现有特征进行多项式展开，生成新的特征。例如，对年龄进行平方、立方等操作。

（3）对数、指数变换：通过对现有特征进行对数或指数变换，改变特征的分布形态，提取更多信息。

（4）统计特征：通过统计数据的分布、聚合或变异程度等属性，生成新的特征。例如，计算均值、标准差、最大值、最小值等。

（5）时间特征：针对时间序列数据，可以衍生出小时、天、周、月、季度等时间单位的特征。

（6）文本特征：对文本数据进行分词、提取关键词、统计词频等操作，生成文本特征。

特征衍生的目的是为了更好地描述数据的特征，提取潜在的信息，以便更好地支持建模和预测任务。通过引入新的特征，可以增加模型的表达能力，提高模型的性能和泛化能力。然而，在进行特征衍生时需要谨慎操作，避免引入过多冗余或无关的特征，以及注意处理特征间的相关性和共线性。

3.2 示例

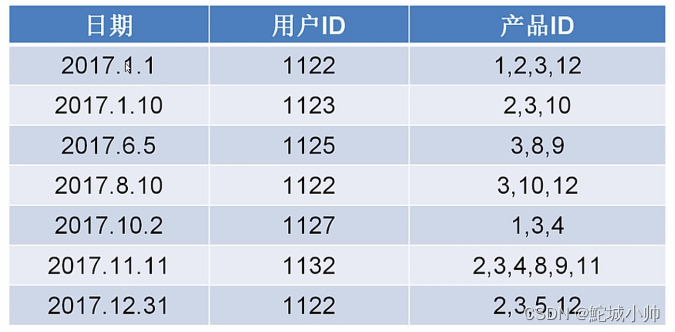
直接进行分析，我们仅能得到日期、用户Id、产品ID三个信息。通过特征衍生，我们可以知道其他特征，比如：从用户角度衍生，可以得到用户购买习惯，购买次数等信息（ID为1122的用户购买了三次商品）。另外，还可以从商品角度衍生，得到商品特征、是否为快消品、是否有季节影响（ID为3的商品每个用户在每个季节都有用，说明可能是快消品；而2可能是季节性的商品）。从关系角度衍生，可以知道某商品是不是用户常卖的、用户一般会怎么搭配。

4. HR表的特征预处理

import pandas as pd
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from sklearn.decomposition import PCA
from sklearn.preprocessing import LabelEncoder

def hr_preprocessing(sl=False, le=False, npr=False, amh=False, tsc=False, wa=False, pl5=False, dp=False, slr=False, lower_d=False, ld_n=1):
    # 读取HR.csv数据文件为DataFrame对象df
    df = pd.read_csv("../data/HR.csv")

    # 1、清洗数据
    df = df.dropna(subset=["satisfaction_level", "last_evaluation"])  # 删除包含空值的行
    df = df[df["satisfaction_level"] <= 1][df["salary"] != "nme"]  # 去除满意度超过1和工资为"nme"的行

    # 2、得到标注
    label = df["left"]  # 标签列
    df = df.drop("left", axis=1)  # 从原始数据中删除标签列

    # 3、特征选择（缺失相关代码）

    # 4、特征处理
    scaler_lst = [sl, le, npr, amh, tsc, wa, pl5]  # 需要进行标准化或归一化处理的特征列表
    column_lst = ["satisfaction_level", "last_evaluation", "number_project",
                  "average_monthly_hours", "time_spend_company", "Work_accident",
                  "promotion_last_5years"]  # 对应的列名

    for i in range(len(scaler_lst)):
        if not scaler_lst[i]:
            # 进行归一化处理
            df[column_lst[i]] = MinMaxScaler().fit_transform(df[column_lst[i]].values.reshape(-1, 1)).reshape(1, -1)[0]
        else:
            # 进行标准化处理
            df[column_lst[i]] = StandardScaler().fit_transform(df[column_lst[i]].values.reshape(-1, 1)).reshape(1, -1)[0]

    scaler_lst = [slr, dp]  # 需要进行独热编码或映射处理的特征列表
    column_lst = ["salary", "department"]  # 对应的列名

    for i in range(len(scaler_lst)):
        if not scaler_lst[i]:
            if column_lst[i] == "salary":
                # 将工资进行映射处理
                df[column_lst[i]] = [map_salary(s) for s in df["salary"].values]
            else:
                # 将部门进行标签编码处理
                df[column_lst[i]] = LabelEncoder().fit_transform(df[column_lst[i]])

            # 进行归一化处理
            df[column_lst[i]] = MinMaxScaler().fit_transform(df[column_lst[i]].values.reshape(-1, 1)).reshape(1, -1)[0]
        else:
            # 进行独热编码处理
            df = pd.get_dummies(df, columns=[column_lst[i]])

    if lower_d:
        # 进行降维处理
        return PCA(n_components=ld_n).fit_transform(df.values), label

    return df, label

d = dict([("low", 0), ("medium", 1), ("high", 2)])

def map_salary(s):
    return d.get(s,0)
def main():
    features,label=hr_preprocessing()
if __name__=="__main__":
    main()