目录

前言： 

150. 逆波兰表达式求值 - 力扣（LeetCode）

239. 滑动窗口最大值 - 力扣（LeetCode）

 总结：

---

前言： 

本片仍然是利用栈与队列的思想来解决实际问题，希望各位小伙伴可以和我一起坚持下去，征服力扣。

150. 逆波兰表达式求值 - 力扣（LeetCode）

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

有效的算符为 '+'、'-'、'*' 和 '/' 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。

在这里我们要先介绍一下什么是逆波兰表达式：
        逆波兰表达式，又称后缀表达式，是一种数学表达式的表示方法。在逆波兰表达式中，操作符在操作数之后，因此也被称为后缀表示法。例如，表达式 "3 + 4" 在逆波兰表达式中表示为 "3 4 +"。逆波兰表示法可以通过栈来实现，首先将所有操作数入栈，每当遇到一个操作符时，弹出栈顶的两个操作数进行运算，并将运算结果再次压入栈中，直到整个表达式处理完毕。与传统的中缀表达式相比，逆波兰表达式的优点是可以不用考虑运算符优先级的问题。 具体文章可以看【夜深人静学数据结构与算法 | 第二篇】后缀（逆波兰）表达式_我是一盘牛肉的博客-CSDN博客 ​​​​​​

非常建议大家先看这篇文章在做这道题，理解了逆波兰运算的思想之后，这道题根本不难！

解法：

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> d1;
        for (int i = 0; i < tokens.size(); i++) {
            if (tokens[i] != "+" && tokens[i] != "-" && tokens[i] != "*" && tokens[i] != "/") {
                d1.push(stoi(tokens[i]));
            }
            if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {
                int a = d1.top();
                d1.pop();
                int b = d1.top();
                d1.pop();
                int sum = 0;
                if (tokens[i] == "+") {
                    sum = b + a;
                    d1.push(sum);
                }
                else if (tokens[i] == "-") {
                    sum = b - a;
                    d1.push(sum);
                }
                else if (tokens[i] == "*") {
                    sum = b * a;
                    d1.push(sum);
                }
                else if (tokens[i] == "/") {
                    sum = b / a;
                    d1.push(sum);
                }
            }
        }
        int final = d1.top();
        return final;
    }
};

 这里由于提供的数组是char类型的，我们自己创建的栈是int类型的，因此入栈的时候需要强制类型转换：stoi是C++标准库中string类型转int类型的函数，d1.push(stoi(tokens[i]))则将字符串类型的元素tokens[i]转换为整数类型并且将其压入栈d1当中。这段代码的作用是将不是操作符的元素压入栈中，以便计算逆波兰表达式时使用。

​​​​​​​239. 滑动窗口最大值 - 力扣（LeetCode）

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

 解法1：双指针思路时间复杂度为O（nums.size()*k），但是这种解法无法解决最后一个测试用例（也就是待测试数组元素极多的情况下），会存在超时问题。而这道题的难点就在于如何解决暴力超时的问题，遍历数组我们无法忽略，因此应该是如何查找k个元素里面的最大值，这是优化时间复杂度的关键

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int>d1;
        int left=0;
        int right=k-1;
        int max=1;
        int temp=0;
        for(int i=0;i<nums.size();i++)
        {
            if(max>nums[i])
            {
                temp=nums[i]-1;
                max=temp;
            }
        }
        while(right<=nums.size()-1)
        {
            for(int i=left;i<=right;i++)
            {
                if(max<nums[i])
                {
                    max=nums[i];
                }
            }
            d1.push_back(max);
            left++;
            right++;
            max=temp;
        }
        return d1;
    }
};

解法2：队列解法

我们抛弃了传统的统计窗口数值时使用的for循环从（left到right），采用了队列的思想，我们就创建一个k长度的队列，每一次更新队列都是去尾添头，这样就省略了一个for循环，大大降低了时间复杂度

此时我们建立一个队列，这个队列的最大值总是在头部，这样我们只需要让队列遍历这个数字，每次输入自己的头部最大值就好了。

class Solution {
private:
    class structQueue { 
    public:
        deque<int> que; 
      
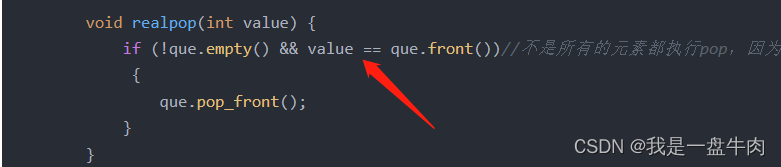
        void realpop(int value) {
            if (!que.empty() && value == que.front())//不是所有的元素都执行pop，因为有的元素进入这个队列之后如果后面有值大于他就 会被顶出去，因此我们这里pop的是真正存在的值。
             {
                que.pop_front();
            }
        }
        //我们一直pop掉比value小的值
        void push(int value) {
            while (!que.empty() && value > que.back()) {
                que.pop_back();
            }
            que.push_back(value);

        }
        //这样头部始终都是最大值。
        int front() {
            return que.front();
        }
    };
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> result;
        structQueue que;      
        for (int i = 0; i < k; i++) {
            que.push(nums[i]);
        }
        result.push_back(que.front()); 
        for (int i = k; i < nums.size(); i++) {
            que.realpop(nums[i - k]); 
            que.push(nums[i]); 
            result.push_back(que.front()); 
        }
        return result;
    }
};

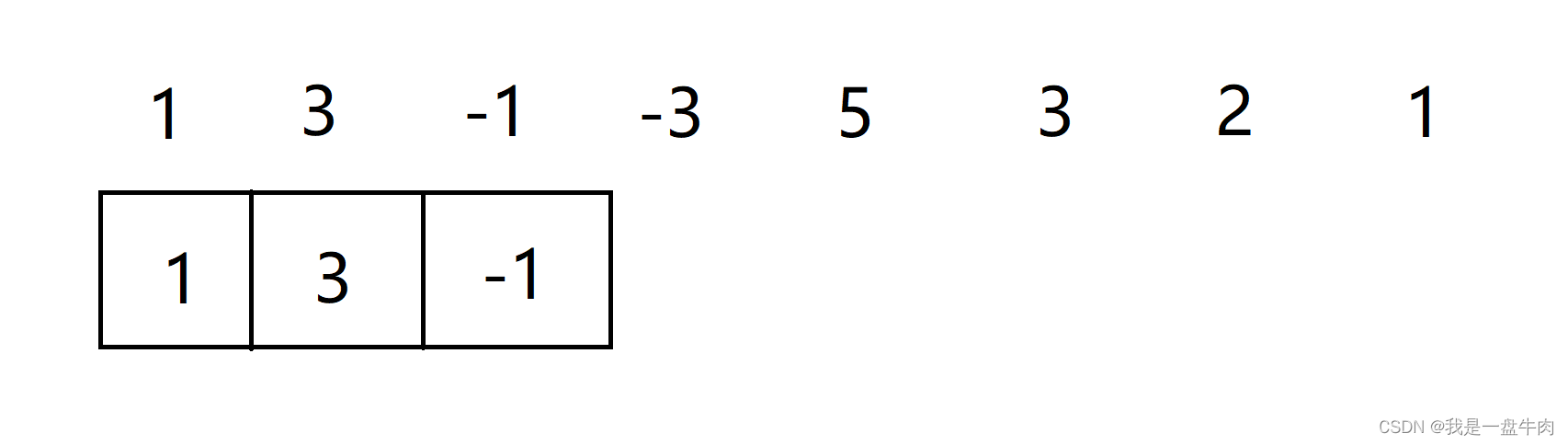
题解二讲解：假设我们要求1，3，-1，-3，5，3，2，1数组，k值=3时，滑动窗口的最大值 

我们在让数组元素进队的时候为了让头部始终都是最大值，采取以下操作：

1.如果新入的数字比队列里的元素都大，我们就弹出队列里的元素，让这个新入的数字入队成为头部。

本来元素挨个入队后：

进行操作后（因为1比3小，我们就让1弹出）结果为3：

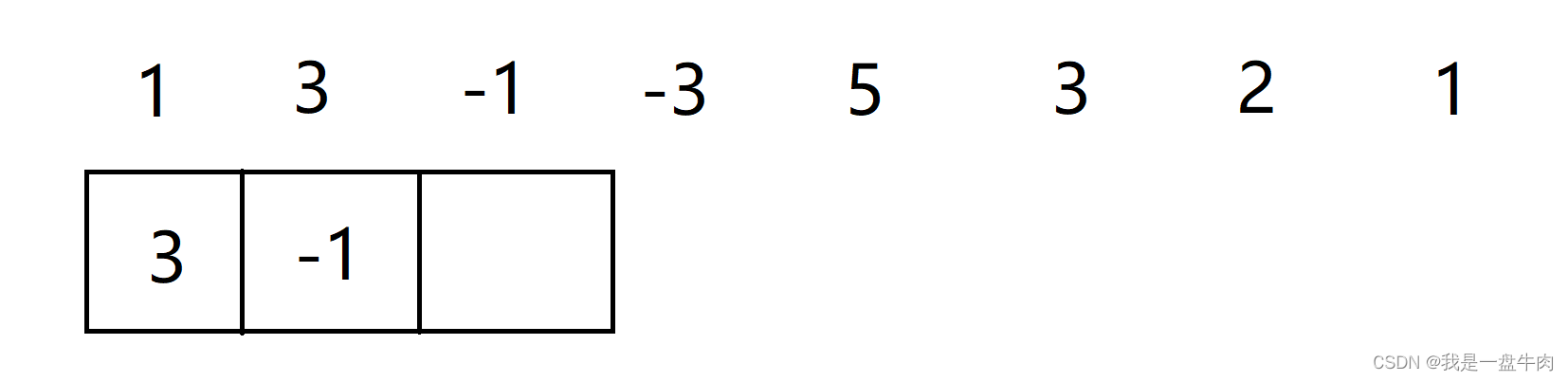
 得到最大值为3，队列向后移动，-3小于前两个值，因此不弹出，结果为3 3

 此时再向后移动，因为5大于所有的数字，因此全部弹出，结果为3 3 5

 再向后移动一位，3比5小，录入其中，结果为3 3 5 5；

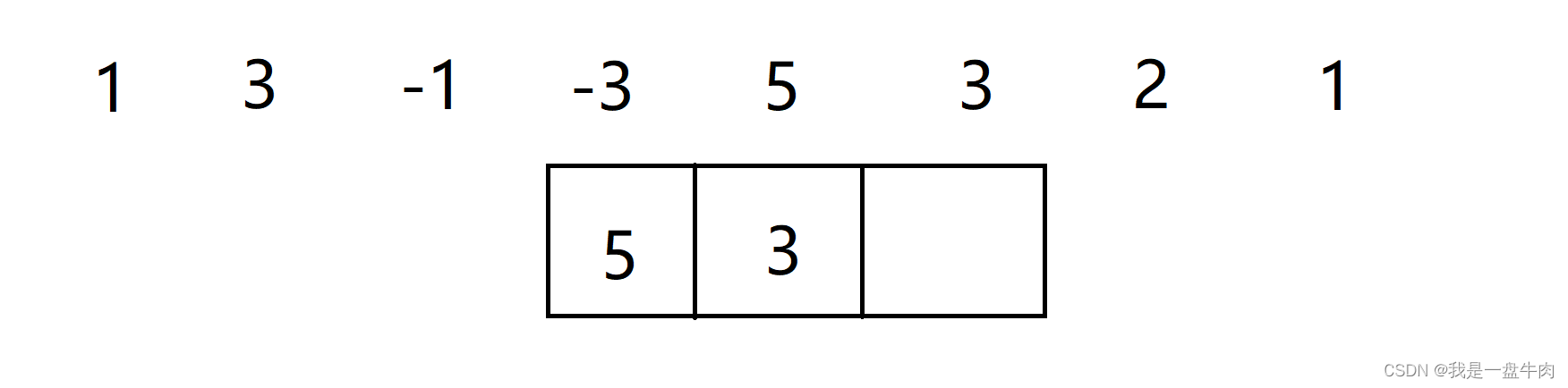
 再向后移动一位，2比5小，录入其中，结果为3 3 5 5 5：

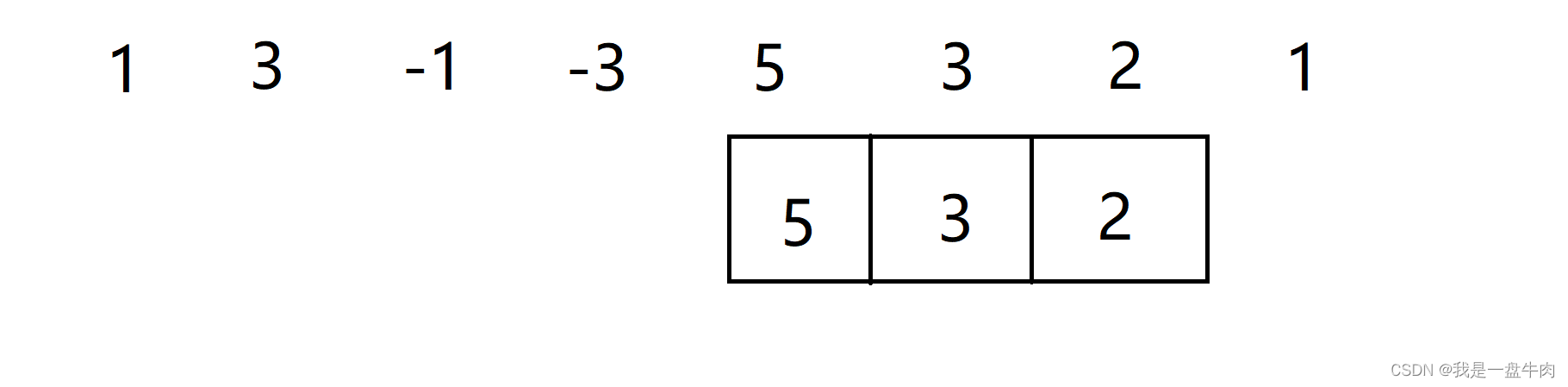
 再向后移动一位，因为此时队列已满，因此我们要弹出末尾元素5，然后再录入，因为整个队列都是降序，因此5弹出之后的队头仍然是整个队的最大值，结果为3 3 5 5 5 3.

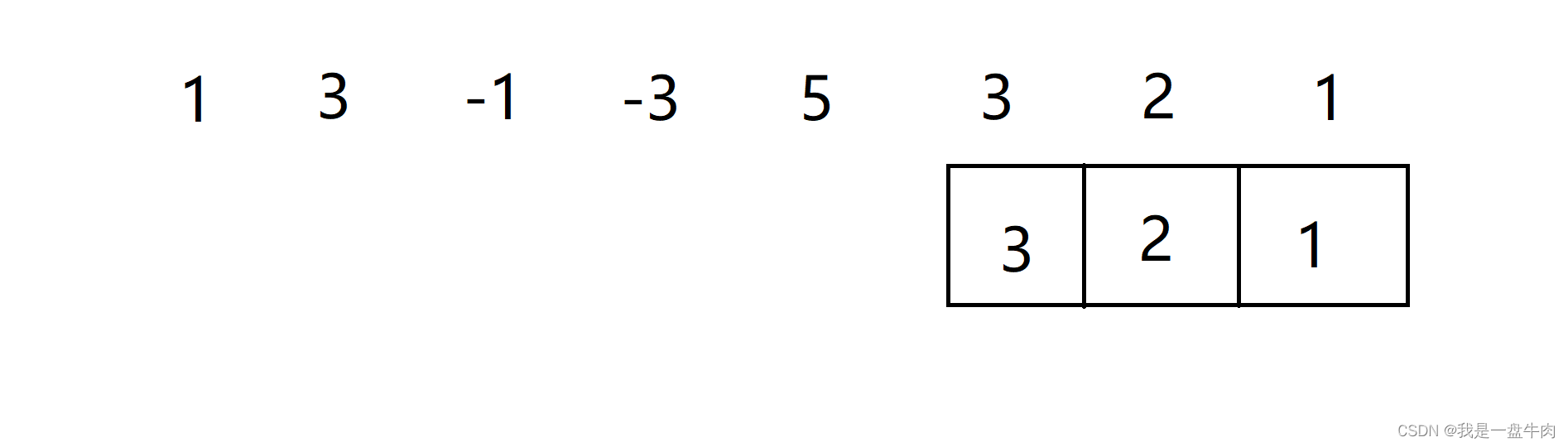
为了方便阅读，我们自己在入口那里写的是将后面的数插入到队列中，将队列末尾的数删去。

但是实际上因为我们总是在维护头部的数据最大，因此我们在插入的时候就已经删除了部分数据，例如最开始的时候数列应该是1，3，-1.但是由于1比3小，绝对不可能成为这个窗口的最大值，因此我们就已经删除了1，那么在插入之后，我们实际上就不需要对末尾的数进行删除，但是为了方便阅读，我们还是加上了删除末尾元素，那么我们就在删除的时候进行判断，如果此时要删除的数字是末尾元素的话，再进行删除(参考情况5 3 2到3 2 1)，此时就是因为之前一直符合递减数列（5并没有机会弹出），1插入不进去，我们就要手动删除末尾元素5，也就是利用我们自己写的删除函数。

插入的时候就已经弹出了。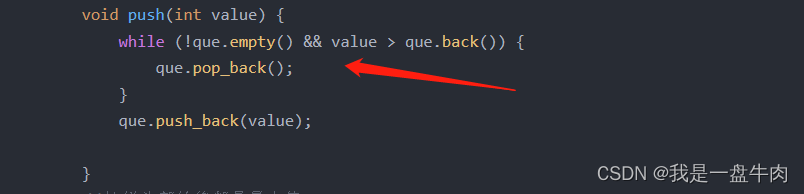

 队列满了之后删除头部：

 总结：

        这两道题一道用到了队列，一道用到了栈，都是很不错的经典例题，可以极大的提高我们对于队列和栈的应用水平，我们应该把这两个题吃透，搞清楚背后的实现代码逻辑。

如果我的内容对你有帮助，请点赞，评论，收藏。创作不易，大家的支持就是我坚持下去的动力！