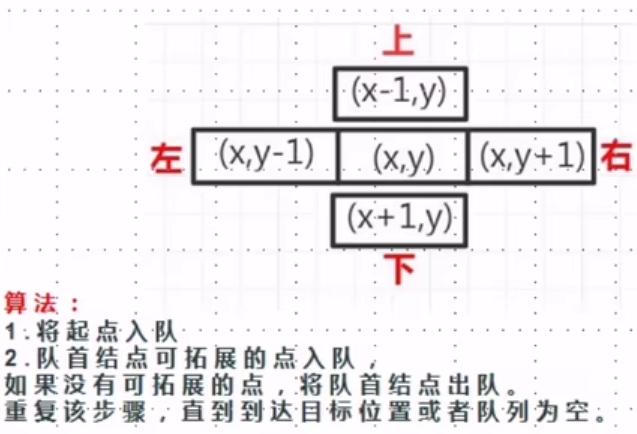
广度优先搜索BFS(Breadth First Search)也称为宽度优先搜索,它是一种先生成的结点先扩展的策略,类似于树的层次遍历。
在广度优先搜索算法中,解答树上结点的扩展是按它们在树中的层次进行的。首先生成第一层结点,同时检查目标结点是否在所生成的结点中,如果不在,则将所有的第一层结点逐一扩展,得到第二层结点,并检查第二层结点是否包含目标结点,……,对层次为n+1的任一结点进行扩展之前,必须先考虑层次完层次为n的结点的每种可能的状态。因此,对于同一层结点来说,求解问题的价值是相同的,可以按任意顺序来扩展它们。通常采用的原则是先生成的结点先扩展。
为了便于进行搜索,要设置一个表存储所有的结点。由于在广度优先搜索算法中,要满足先生成的结点先扩展的原则,所以存储结点的表一般采用队列这种数据结构。
在编写程序时,可用数组q模拟队列。
front和rear分别表示队头指针和队尾指针,初始时front=rear=0。
元素x入队操作为 q[rear++]=x;
元素x出队操作为 x =q[front++];
广度优先搜索算法的搜索步骤一般是:
(1)从队列头取出一个结点,检查它按照扩展规则是否能够扩展,如果能则产生一个新结点。
(2)检查新生成的结点,看它是否已在队列中存在,如果新结点已经在队列中出现过,就放弃这个结点,然后回到第(1)步。否则,如果新结点未曾在队列中出现过,则将它加入到队列尾。
(3)检查新结点是否目标结点。如果新结点是目标结点,则搜索成功,程序结束;若新结点不是目标结点,则回到第(1)步,再从队列头取出结点进行扩展。
最终可能产生两种结果:找到目标结点,或扩展完所有结点而没有找到目标结点。
如果目标结点存在于解答树的有限层上,广度优先搜索算法一定能保证找到一条通向它的最佳路径,因此广度优先搜索算法特别适用于只需求出最优解的问题。当问题需要给出解的路径,则要保存每个结点的来源,也就是它是从哪一个节点扩展来的。
对于广度优先搜索算法来说,问题不同则状态结点的结构和结点扩展规则是不同的,但搜索的策略是相同的。广度优先搜索算法的框架一般如下:
void BFS()
{
队列初始化;
初始结点入队;
while (队列非空)
{
队头元素出队,赋给current;
while (current 还可以扩展)
{
由结点current扩展出新结点new;
if (new 重复于已有的结点状态) continue;
new结点入队;
if (new结点是目标状态)
{
置flag= true; break;
}
}
}
}
对于不同的问题,用广度优先搜索法的算法基本上都是一样的。但表示问题状态的结点数据结构、新结点是否为目标结点和是否为重复结点的判断等方面则有所不同。对具体的问题需要进行具体分析,这些函数要根据具体问题进行编写。
接下来从一个经典的迷宫问题引入:哔哩哔哩完整视频讲解

关于搜索方向:
测试用例:
5 4
1 1 2 1
1 1 1 1
1 1 2 1
1 2 1 1
1 1 1 2
1 1 4 3
输出:
7
详细代码:
#include<iostream>
#include<queue>
using namespace std;
int m, n;//输入的地图大小 m行 n列
int map[100][100];//地图数组 0为边界 1为可走 2为障碍
int v[100][100];//访问数组 1为已访问 0为未访问
//四个方向: 右、下、左、上
int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};
//标识是否搜索到
bool flag = false;
class Point { //创建节点
public:
int x;
int y;
int step;
};
queue<Point> r;//创建队列
int main() {
cin >> m >> n;
//从1开始循环 可以避免数组越界 因为最外层有一圈0 来作“墙”
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
cin >> map[i][j];
}
}
int start_x, start_y,end_x,end_y;
cin >> start_x >> start_y >> end_x >> end_y;
//BFS 广度优先搜索
Point start;
start.x = start_x;
start.y = start_y;
start.step = 0;
r.push(start);//将起点入队
v[start.x][start.y] = 1;//把起点设置为已访问 1
while (!r.empty()) {
int x = r.front().x;
int y = r.front().y;
if (x == end_x && y == end_y) /*找到终点*/{
flag = true;
cout << r.front().step;
break;
}
//从四个方向搜索
for (int i = 0; i <= 3; i++) {
int tx = x + dx[i];
int ty = y + dy[i];
if (map[tx][ty] == 1 && v[tx][ty] == 0) {//如果地图能走,且未访问
//入队
Point temp;
temp.x = tx;
temp.y = ty;
temp.step = r.front().step + 1;
r.push(temp);
v[tx][ty] = 0;
}
}
r.pop();//四个方向搜索完了需要将队首元素出队
}
if (flag==false) {
cout << "没有找到";
}
return 0;
}
/*测试用例:
5 4
1 1 2 1
1 1 1 1
1 1 2 1
1 2 1 1
1 1 1 2
1 1 4 3
*/
宽搜BFS 和 深搜DFS 的比较: