对于现在的CPU来说，基本上都在硬件上实现了CRC校验。但我们还是想用软件来实现一下CRC的代码，这样可以更深入地理解里面的原理。所以这一节就来详细地解释如何使用查表法从软件上来实现CRC-32的校验。另外，CRC还有一种反转的情况，实际上反转和不反转没有什么太大的区别，主要是需求和标准的不同。

1 找规律

再来看一下上一节中的例子，被除数为100100，除数为1101的计算过程：

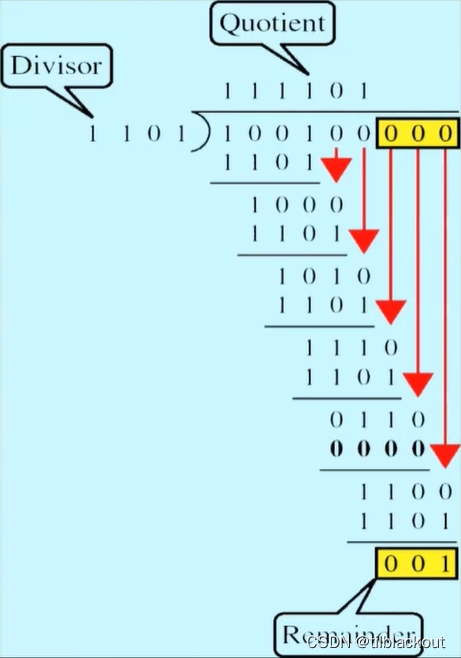
我们来找一下规律，思考一下在计算机中应该如何实现。不难发现以下规律：

• 除数的最高位一定是1，因为我们用的是它所代表的多项式的最高阶组成的数字
• 对于除数来说，如果它的最高位不是1的话，就"除不动"，什么都不做，左移一位，继续判断。
• 由于做的是异或运算，所以当前的结果不一定要"减得动"被除数，只需要满足除数最高位为1，就和被除数做异或运算，然后再左移一位

2 查表法原理

如果我们要软件上实现CRC的话，要一位一位的做这些运算，效率是非常低的，所以我们就想能不能每8位计算一次，因为每个特定的数字与这个被除数的经过8次移位操作得到的异或结果都是相同的。
（1）为什么不每16位计算一次？
这样就要保存$2^{16}$个uint16_t类型的数据，一个表格就有128KB，都比很多单片机的Flash要大了
（2）每8位计算一次的理论依据是什么
我们又知道$CRC(0)=0$，然后由前面分析出的特性，我们可以推导出这个公式：$CRC(A+B)=CRC(A)+CRC(B)$。

现在举个例子，假如我们想求$CRC(0\times abcdef12)$，他就可以等价于：
$CRC(0\times abcdef12)=CRC(0\times ab000000)+CRC(0\times 00cdef12)=CRC(0\times ab)+CRC(0\times cd)+CRC(0\times ef)+CRC(0\times 12)$

加入我们定义一个8位的查表表格，这样我们就可以把本来每次要进行的32次移位或异或的运算缩短为了4次。

3 CRC32代码C语言实现

3.1 CRC32表格生成

经过前面的分析，我们知道，我们就是需要给uint8_t范围内(0~255)的每一个数做一下模二除法，然后将得到的结果保存到一个类型为uint8_t、大小为256的表格中。我们只需要判断CRC的最高位是否为1，若为0则左移一位，若为1则先将crc左移1位，然后和多项式做异或运算。CRC32表格生成代码如下：

void GenerateTable(uint32_t polynomial)
{
	for (int byte = 0; byte < 256; ++byte)
	 {
		uint32_t crc = byte;
		
		for (int bit = 32; bit > 0; --bit)
		{
			if (crc & 0x80000000)
			{
				  crc = (crc << 1) ^ polynomial;
			}
			else
			{
				  crc <<= 1;
			}
		}
		crcTable[byte] = crc;
	 }
}

如果你把上面的代码和前面的例子那张图做对比的话，我相信不少人会想为什么在CRC最高位为1的时候，执行的不是crc = (crc ^ polynomial) << 1？

别忘了，对于CRC32来说，它的多项式所对应的二进制是有33位的，实际上我们无法用一个uint32_t的变量来保存这个多项式。但是我们知道，CRC32的多项式的最高位一定是1，所以这里我们就保存低32位作为polynomial。当代码中CRC的最高位为1时，它与CRC32的最高位异或的结果也一定是0。所以这里就先将CRC右移一位，然后与多项式异或，这样循环32次，就得到在多项式polynomial下的byte所对应的CRC，将其存入crcTable中。

3.2 CRC查表代码实现

有了前面的表格，我们使用下面的函数就能计算长度为len的字符串msg的CRC32了，在循环中，将CRC的高八位所对应的数在CRC32表格中的结果与上次计算出来的CRC右移八位的结果进行异或，最后就得到了这个字符串的CRC结果了。

unsigned int calcMsgCRC(char *msg, unsigned int len)
{
    unsigned long crc = 0;
    for (int n = 0; n < len; n++)
    {
    	uint8_t c = msg[n] & 0xff;
        crc = crcTable[(crc >> 24) ^ c] ^ (crc << 8);
    }
    return crc;
}

• 在某些协议的CRC算法中，CRC有一个固定的初始值，求出来CRC结果后也还需要异或一个固定数

另外，在有些场合下，比如从串口中获取最新的固件来升级系统，固件的完整性也通过CRC校验。在有的设备中没有那么大的内存将整个buffer保存下来，再计算整个buffer的CRC校验。对于这种情况，我们可以一段一段地计算CRC，然后将前一次CRC的结果赋值给函数中unsigned long crc的初始值。也就是calcMsgCRC函数的参数也要多加一个lastCRC。

• 我之前从NXP SDK提取了一个分段CRC的代码，大家也可以用这个框架：C语言 CRC32分段计算实现

4 CRC反转

有时你可能会发现一些标准协议的CRC的表格和你生成的就是不一样。这可能是因为CRC有两种实现方式：

• 非反转CRC：数据的每一位从最高位到最低位依次处理
• 反转CRC：数据的每个字节或比特位的处理顺序可以根据需求进行反转。

4.1 CRC32的标准反转函数

代码如下所示：

uint32_t Reverse(uint32_t value)
{
  value = ((value & 0xAAAAAAAA) >> 1) | ((value & 0x55555555) << 1);
  value = ((value & 0xCCCCCCCC) >> 2) | ((value & 0x33333333) << 2);
  value = ((value & 0xF0F0F0F0) >> 4) | ((value & 0x0F0F0F0F) << 4);
  value = ((value & 0xFF00FF00) >> 8) | ((value & 0x00FF00FF) << 8);
  value = (value >> 16) | (value << 16);
  return value;
}

（1）将value的奇数位和偶数位分别取出，并将奇数位右移1位，偶数位左移1位，然后将它们进行按位或运算。这样可以交换奇数位和偶数位的值。
（2）将value的每2位分组，其中每组的高位和低位进行比特顺序的反转。同样，采用按位与和按位或运算，将高位和低位进行交换。
（3）将value的每4位分组，同样对每组的高位和低位进行比特顺序的反转。
（4）将value的每8位分组，同样对每组的高位和低位进行比特顺序的反转。
（5）将value的高16位和低16位进行比特顺序的反转

4.2 CRC输入/输出反转

另外，我们可以选择对CRC在输入时反转，也可以选择对CRC在输出时反转，当然也可以选择都反转。所以这时候反转CRC32表格生成函数需要做小小的修改：

void GenerateTable(uint32_t polynomial, bool reflectIn, bool reflectOut)
{
    for (int byte = 0; byte < 256; ++byte)
    {
        uint32_t crc = (reflectIn ? (Reverse(uint32_t(byte)) >> 24) : byte);

        for (int bit = 32; bit > 0; --bit)
        {
            if (crc & 0x80000000)
            {
                crc = (crc << 1) ^ polynomial;
            }
            else
            {
                crc <<= 1;
            }
        }
        crcTable[byte] = (reflectOut ? Reverse(crc) : crc);
    }
}

对于反转CRC的计算函数来说(假设输入和输出都反转)，要这样修改：

unsigned int calcMsgCRCReverse(char *msg, unsigned int len)
{
    unsigned long crc = 0;
    for (int n = 0; n < len; n++)
    {
        uint8_t c = msg[n] & 0xff;
        c = Reverse(c);
        crc = crcTable[(crc ^ c) & 0xFF] ^ (crc >> 8);
    }
    return Reverse(crc);
}

使用反转CRC或非反转CRC时，CRC表格的生成和查找方法也会有所不同。这两种方式在实际应用中并没有明显的性能或准确性差异，选择哪种方式主要取决于应用的需求和标准。