Summary

在pytorch_tutorial中给出了一个训练流程的简要介绍：
Training a model is an iterative process;训练模型是一个迭代的过程。
in each iteration the model makes a guess about the output, calculates the error in its guess (loss), 在每次迭代中，模型会对输出结果做一个猜测，并且计算这个结果和目标结果之间的差距。
collects the derivatives of the error with respect to its parameters (as we saw in the previous section), 然后会进行求导的过程，也就是前面的backward()。
and optimizes these parameters using gradient descent。并且使用梯度下降的方法来对参数进行优化。

我们首先在这里给出一个完整的训练模型的代码，再在后面分部分进行解释。
这里使用的dataset是我们在第一章中提到过的Cifar10dataset。需要注意的是，第一章讲解的时候为了省事，我们在10000张test图像上重新进行了数据集的划分。在实际训练中，请使用cifar10的完整数据。
pytorch本身的datasets中也提供了Cifar10的数据，具体用法在第一章有讲解。

import os
import cv2
import torch
import pandas as pd
import torch.nn.functional as F
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from torchvision import transforms 

# 定义自己的dataset，这个dataset会从csv中获取图像的path和label
class CustomImageDataset(Dataset):
    def __init__(self, annotations_file, transform=None, target_transform=None):
        self.img_labels = pd.read_csv(annotations_file)
        self.transform = transform
        self.target_transform = target_transform

    def __len__(self):
        return len(self.img_labels)

    def __getitem__(self, idx):
        img_path =  self.img_labels.iloc[idx, 0] #图像的路径
        image = cv2.imread(img_path) #读取图像
        label = self.img_labels.iloc[idx, 1] #图像的label
        if self.transform:
            image = self.transform(image)
        if self.target_transform:
            label = self.target_transform(label)
        return image, label
transform = transforms.Compose(
     [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))]
) # 使用的transform，在不考虑模型训练效果得情况下，暂时使用比较简单的transform作为例子。

train_csv_path = '' # 给出自己的训练集的csv的位置
training_data = CustomImageDataset(train_csv_path,transform)
test_csv_path = '' #给出自己的测试集的csv的位置
test_data = CustomImageDataset(test_csv_path,transform)
train_dataloader = DataLoader(training_data, batch_size=64,shuffle = True) # 训练集的shuffle设置为True，保证随机性
test_dataloader = DataLoader(test_data, batch_size=64, shuffle = False) # shuffle可以设为False

# 定义一个比较简陋的net,改代码来自pytorch_tutorial
class NeuralNetwork(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = torch.flatten(x, 1) # flatten all dimensions except batch
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x
model = NeuralNetwork()

# 训练过程的每个epoch的操作，代码来自pytorch_tutorial
def train_loop(dataloader, model, loss_fn, optimizer):
    size = len(dataloader.dataset)
    # Set the model to training mode - important for batch normalization and dropout layers
    # Unnecessary in this situation but added for best practices
    model.train()
    for batch, (X, y) in enumerate(dataloader):
        optimizer.zero_grad() # 重置梯度计算
        # Compute prediction and loss
        pred = model(X)
        loss = loss_fn(pred, y)

        # Backpropagation
        loss.backward() # 反向传播计算梯度
        optimizer.step() # 调整模型参数
        

        if batch % 10 == 0:
            loss, current = loss.item(), (batch + 1) * len(X)
            print(f"loss: {loss:>7f}  [{current:>5d}/{size:>5d}]")


def test_loop(dataloader, model, loss_fn):
    # Set the model to evaluation mode - important for batch normalization and dropout layers
    # Unnecessary in this situation but added for best practices
    model.eval()
    size = len(dataloader.dataset)
    num_batches = len(dataloader)
    test_loss, correct = 0, 0

    # Evaluating the model with torch.no_grad() ensures that no gradients are computed during test mode
    # also serves to reduce unnecessary gradient computations and memory usage for tensors with requires_grad=True
    with torch.no_grad():
        for X, y in dataloader:
            pred = model(X)
            test_loss += loss_fn(pred, y).item()
            correct += (pred.argmax(1) == y).type(torch.float).sum().item()

    test_loss /= num_batches
    correct /= size
    print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")

learning_rate = 1e-3
momentum=0.9
batch_size = 64
epochs = 20

loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate,momentum=momentum)

for t in range(epochs):
    print(f"Epoch {t+1}\n-------------------------------")
    train_loop(train_dataloader, model, loss_fn, optimizer)
    test_loop(test_dataloader, model, loss_fn)
print("Done!")

Autograd

在模型训练中，使用最多的算法是反向传播back propagation。反向传播算法，会根据损失函数相对给定的参数的梯度对模型的参数(权重)进行调整。
幸运地是，计算梯度和反向传播的过程都不需要我们来实现，pytorch提供了torch.autograd的方法来支持所有计算图中梯度的自动计算。
关于计算图，随手搜了一下，可以参考计算图（Computational Graph）的角度理解反向传播算法（Backpropagation）这篇文章。

Functions ()

你在tensors进行计算操作，你将不同的function应用在tensor上并构成了一个完整的计算图。这些function本质上都属于torch.autograd.Function()类。
假如你想要使用自定义的function()类，首先需要在创建你的函数时继承torch.autograd.Function，并手动实现forward()和backward函数()。并且在调用函数时，需要使用apply()，而不是直接使用forward()。
我们以pytorch官方tutorial中给出的代码为例子：

class Exp(Function):
    @staticmethod
    def forward(ctx, i):
        result = i.exp()
        ctx.save_for_backward(result)
        return result
    @staticmethod
    def backward(ctx, grad_output):
        result, = ctx.saved_tensors
        return grad_output * result
# Use it by calling the apply method:
output = Exp.apply(input)

可以看到示例代码在最开始定义Exp()类时，就将其作为Function的子类。并且手动定义了forward()和backward()函数。在最后使用的时候也是用了Exp.apply()来调用forward的过程。
不管是Module()还是Function()都不推荐直接调用forward()。
在实际使用中，我们直接使用pytorch提供的各种function就可以，需要自己定义的情况很少。

Gradient

梯度在神经网络的优化迭代中扮演了很重要的角色。在创建一个tensor时，我们可以使用 requires_grad = True为我们的tensor赋予梯度，拥有梯度的参数才可以在反向传播中被优化。
我们在tensor上执行function操作来构建一个计算图，这个function不仅知道我们前向传播的顺序，也知道我们反向传播是如何计算的。反向传播的梯度计算方法，被存储在tensor的grad_fn中。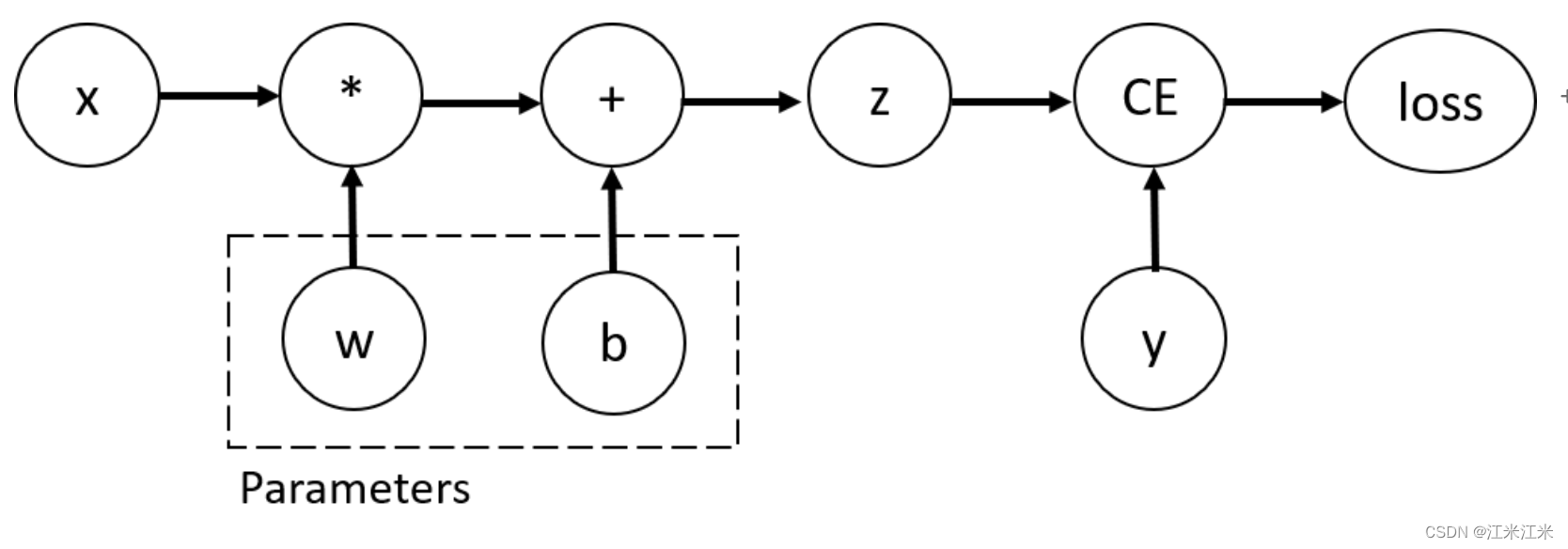
我们使用tutorial中给出的一个例子。
在这里x是我们的input，y是我们的target，w和b是一个带有梯度的Parameter，即我们希望优化的参数。z是我们的w*x+b得到的运算结果。
我们使用grad_fn来获得反向传播的梯度计算方法。

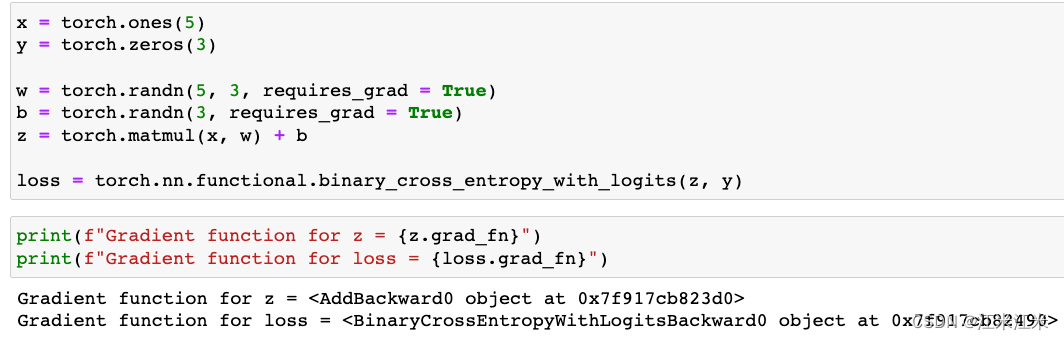
假如我们把requires_grad设置为False，我们的grad_fn就会是None。

Backward()

源码参考： https://pytorch.org/docs/stable/generated/torch.autograd.backward.html?highlight=backward#torch.autograd.backward
为了更新神经网络中的权重参数，我们要用我们的loss相对参数进行求导，而loss.backward()就帮助我们完成了这个过程。
只有requires_grad = True的参数，才能够获得梯度。下面给出了两个例子。
在第一个例子中，我们的w和b的requires_grad都是True，因为在经过loss的反向传播后，我们可以获得两个参数的梯度。

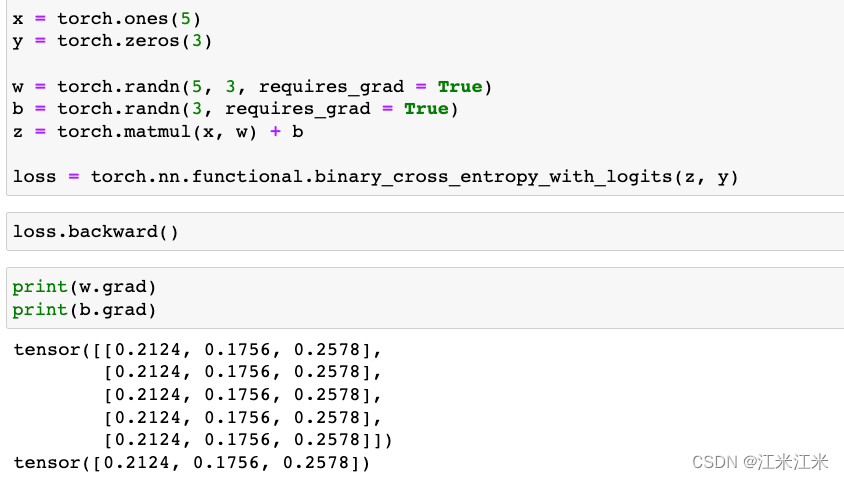
在第二个例子中，我们把b的requires_grad改为了False，经过反向传播后，发现我们获得了w的梯度，但是b的梯度是None。因此我们也不能利用梯度对参数b进行更新。

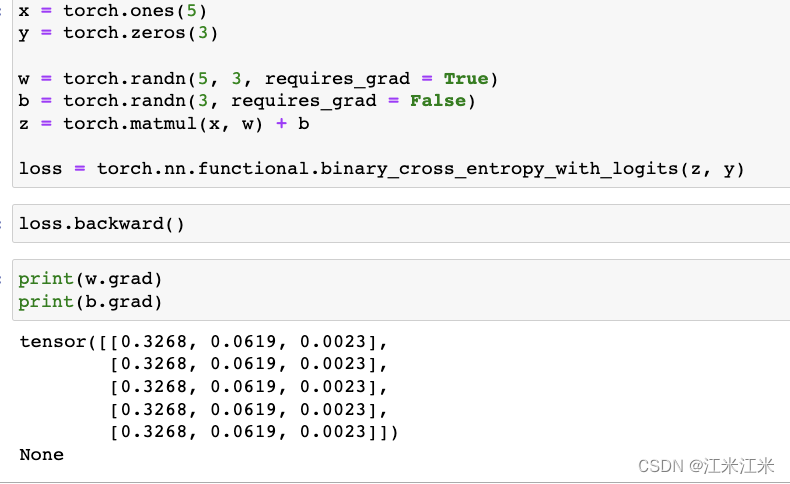
在tutorial中提到We can only perform gradient calculations using backward once on a given graph, for performance reasons. If we need to do several backward calls on the same graph, we need to pass retain_graph=True to the backward call。意思是我们只能使用一次backward()方法，除非把retain_graph设置为true，即使用backward(retain_graph = True)。但是这个方法一般不建议使用，会有性能和表现上的影响。

多次使用backward()方法的例子看https://stackoverflow.com/questions/46774641/what-does-the-parameter-retain-graph-mean-in-the-variables-backward-method，该链接中对为什么要使用retain_graph给出了比较详细的解释。
比如在你使用了两个loss时，你的backward()部分就需要写成：

# suppose you first back-propagate loss1, then loss2 (you can also do the reverse)
loss1.backward(retain_graph=True)
loss2.backward() # now the graph is freed, and next process of batch gradient descent is ready
optimizer.step() # update the network parameters

当然，更好的方法是使用：

loss = loss1 + loss2
loss.backward()

Optimization

Optimization is the process of adjusting model parameters to reduce model error in each training step.
既然我们已经学会了使用pytorch来获得参数的梯度，那么我们现在就要选择使用什么样的方法来进行参数更新。
我们通常使用的参数，除了神经网络中具有梯度的，随着训练进行会迭代更新的参数外，还有一种固定的不会改变的参数，这些参数同样对我们的训练过程产生影响，我们统称为HyperParameters，即超参数。
在创建dataset那一章中，我们曾经提到过batchsize，这也是超参数的一种。
此外，epoch_num(训练轮数)，learning rate(学习率)等也是超参数。

Optimization loop

我们说epoch_num是训练的轮数，一个epoch就是一轮，代表了一个完整的optimization loop(优化循环)。
一个optimization loop是由两部分组成的。

• **Train Loop：**在一个train loop中，我们的模型会遍历整个训练数据，并更新其中的权重参数。
• Validation/Test Loop: 在一个validation loop/test loop中，我们的模型也会遍历对应的数据集，但是不会更强其中的权重参数。

Optimizer

参考文档：https://pytorch.org/docs/stable/optim.html#torch.optim.Optimizer
Optimization algorithm(优化算法)决定了更新模型参数的过程是如何进行的，优化的逻辑在pytorch中被封装到了optimizer中。
pytorch中定义了多个optimizer，这些optimizer都是基于torch.optim.Optimizer实现的：Optimizer。
这些optimizer在初始化时都需要传入两类参数，第一类就是你想要优化的parameters，第二类就是optimizer使用的超参数。
比如我们使用SGD随机梯度下降，它传入的第一个参数就是模型的paramters，第二个是学习率这个超参数。

optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

在一个train loop中，对模型参数的优化发生在三个部分。

1. Call optimizer.zero_grad() to reset the gradients of model parameters. Gradients by default add up; to prevent double-counting, we explicitly zero them at each iteration. 在每次迭代前，使用优化器重置模型参数的梯度。

2. Backpropagate the prediction loss with a call to loss.backward(). PyTorch deposits the gradients of the loss w.r.t. each parameter. 使用反向传播的方法，计算模型参数的梯度。

3. Once we have our gradients, we call optimizer.step() to adjust the parameters by the gradients collected in the backward pass. 使用我们的优化器，对模型参数进行更新。

Learning Rate Schedules

为了方便理解下一部分的内容，在这里进行一些比较简单的关于学习率调度（learning rate schedules）的理论。
梯度下降算法中总是沿着梯度相反的方向来优化我们的模型参数。这里的优化并不是说本次计算得到的梯度是多少，就对我们的参数进行多少改动，而是会按照某个比率进行修正。
比如说，我们计算得到损失函数E相对于参数wi的梯度：
$$d_i(t)=\frac{\partial E}{\partial w_i(t)}$$
我们对参数wi进行更新的步骤，其实是这样的：
$$\begin{gathered} \Delta w_i(t)=-\eta di(t) \\ {w}_i(t+1)=w_i(t)+\Delta w_i(t) \end{gathered}$$
在权重沿着负梯度方向更新时，乘以了一个超参数$\eta$，我们称之为学习率。
这个学习率并不是必须设定成一成不变的，早有研究证明变化的学习率：从较大的学习率开始，后学习率逐渐减小，能使得训练过程中模型收敛的更快，并取得更好的结果。
在下面给出一些学习率调度的方法举例

Time-dependent schedules

基于时间的学习率调度中，学习率$\eta$的大小是由训练时长决定的。
$$\Delta w_i(t)=-\eta (t)d_i(t)$$
可以分成以下三种：
1.Piecewise constant：为每一个epoch提前设定好学习率。
2. Exponential：满足公式$\eta (t)=\eta (0)exp(-t/r)$ 其中r代表训练集的大小。
3. Reciprocal: 满足公式$\eta (t)=\eta (0)(1+t/r{)}^{-c}$

Performance-dependent schedules

固定$\eta$的值，直到验证集上的效果不再提升，此时就对$\eta$进行折半处理。

Training with Momentum

$$\Delta w_i(t)=-\eta d_i(t)+\alpha \Delta w_i(t-1)$$
$\alpha$被称为动量超参数,$\alpha \Delta w_i(t-1)$被称为动量项。本次参数更新的值，不止受学习率影响，也受上次更新的影响。这样可以使权重的变化更加平稳，而不是每次在一个随机的梯度方向上更新。

Adaptive learning rates

在这里我们会介绍三个常用的例子。
1. 以AdaGrad()方法为例子。直接贴一个原理图。

这里的$S_i(t)$每次更新都会累加上一次的梯度平方和。因此作为学习率变化的分母项目$\sqrt{S_i(t)}$总是递增的，因此学习率的变化是单调递减的。当你当前的梯度越大，分母项越大，学习率项反而会更小。
2. 以RMSProp()方法为例子，放一个原理图。

它和AdaGrad()相似的是都使用了一个学习率的分母项，但是在这个算法里它的分母项不是单调递增的。它的分母项由梯度的平方的滑动平均构成。
3. 以Adam()方法为例子，放一个原理图。

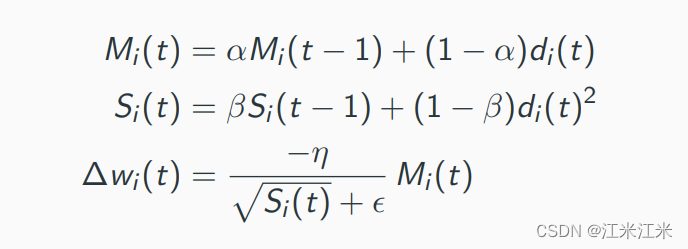
Adam()可以看作是RMSProp()的带动量版本。它每次对参数更新的值不再是学习率直接乘以梯度，而是乘以一个梯度的滑动平均，也被成为momentum-smoothed gradient。

optim.lr_scheluder

pytorch中也提供了一些基于epoch调整学习率的方法。如果你想在使用optimizer的基础上再添加这些学习率调度的方法， 在编写代码时你需要把它添加在学习率更新的后面。
比如说：

optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
scheduler = ExponentialLR(optimizer, gamma=0.9)

for epoch in range(20):
    for input, target in dataset:
        optimizer.zero_grad()
        output = model(input)
        loss = loss_fn(output, target)
        loss.backward()
        optimizer.step()
    scheduler.step()

你还可以将多个学习率调度方法链式连接在一起，每个都会在上一个结果的基础上再次进行调整。
pytorch给了一个模板方便你理解。

scheduler = ...
for epoch in range(100):
    train(...)
    validate(...)
    scheduler.step()