题目描述

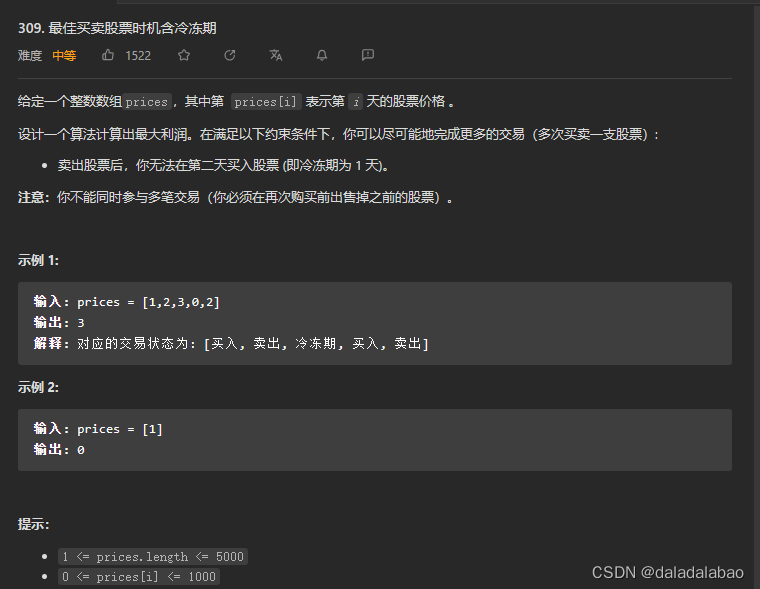
给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。​
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题

动态规划：

• buy[i]表示在第i天之前已经买入的能获得的最大收益；
• sell[i]表示在第i天之前已经卖出的能获得的最大收益；
• coolDown[i]表示在第i天之前没有任何操作或者已经完成交易的能获得的最大收益；

代码首先对基础情况进行了处理，如果价格为空或者长度小于等于1，则无法交易，返回0。

然后初始化第一天的各项值，即：买入价为相反数（因为买了股票意味着花费了钱），售价为0，即还没卖，处于放空状态，冷却期为0，即已完成了当天的所有交易。

接下来就是重要的动态转移方程：

• 当前时刻买进的最大收益等于之前已经购买的最大收益和冷却期结束之后购买股票所获得的收益中最大的那个；
• 当前时刻卖出的最大收益等于之前已经完成的Transactions和当前买入所获取的收益中的最大值；
• 当前时刻放空的最大收益等于之前已经放空的收益和当前卖出所获得的收益中的最大值。

循环结束后，返回sell数组中存储的最后一个元素，即可得到买卖股票的最大收益。

class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length <= 1) {
            return 0;
        }

        int len = prices.length;
        int[] buy = new int[len];
        int[] sell = new int[len];
        int[] coolDown = new int[len];

        buy[0] = -prices[0];
        sell[0] = 0;
        coolDown[0] = 0;

        for (int i = 1; i < len; i++) {
            buy[i] = Math.max(buy[i - 1], coolDown[i - 1] - prices[i]);
            sell[i] = Math.max(sell[i - 1], buy[i - 1] + prices[i]);
            coolDown[i] = Math.max(coolDown[i - 1], sell[i - 1]);
        }

        return sell[len - 1];
    }
}