Matplotlib

在深度学习的实验中，图形的绘制和数据的可视化非常重要。Matplotlib是用于绘制图形的库，使用Matplotlib可以轻松地绘制图形和实现数据的可视化。这里，我们来介绍一下图形的绘制方法和图像的显示方法。

曲线图的绘制

plt.plot()参数分析：

plt.plot(x,y,format_string,**kwargs)

x表示二维坐标中X轴数据（列表或数据，可选）
y表示二维坐标中Y轴数据（列表或数据）
format_string表示控制曲线的格式字符串（线宽，线型，颜色等等），可选
**kwargs表示第二组或更多（x,y,format_string）

import matplotlib.pyplot as plt
import numpy as np

a = np.arange(10)  # 以1为单位，生成0到10的数据
plt.plot(a,a*1.5,'r--.',  a,a*2.5,'g:^',  a,a*3.5,'c-*',  a,a*4.5) # 多组参数，每组3个参数，表示一个图像对象，前两个参数为坐标数据，第个参数控制曲线格式
plt.xlabel("横轴",fontproperties='Kaiti',fontsize=20)
plt.ylabel("纵轴",fontproperties='Kaiti',fontsize=20)
plt.savefig('line',dpi=600,bbox_inches='tight') # 用于保存图片 参数：文件名，分辨率，保存部分参数
plt.show()

在这里插入图片描述

饼图的绘制

plt.pie()参数分析：

import matplotlib.pyplot as plt

plt.pie(x, explode=None, labels=None, colors=None, autopct=None, pctdistance=0.6, shadow=False, labeldistance=1.1, startangle=0, radius=1, counterclock=True, wedgeprops=None, textprops=None,center=0, 0, frame=False, rotatelabels=False, *, normalize=None, data=None)

x即每个扇形的占比的序列或数组
explode如果不是None，则是一个len(x)长度的数组，指定每一块的突出程度；突出显示，设置每一块分割出来的间隙大小
labels为每个扇形提供标签的字符串序列
colors为每个扇形提供颜色的字符串序列
autopct如果它是一个格式字符串，标签将是fmt % pct。如果它是一个函数，它将被调用
shadow阴影
startangle从x轴逆时针旋转,饼的旋转角度
pctdistance, default: 0.6每个饼片的中心与由autopct生成的文本的开头之间距离与半径的比率，大于1的话会显示在圆外
labeldistance, default: 1.1饼状图标签绘制时的径向距离（我认为这个也与8类似是个比率）。如果设置为None，则不绘制标签，而是存储在图例()中使用。

import matplotlib.pyplot as plt

labels = 'Frogs','Hogs','Dogs','Logs' #饼图的标签
sizes = [15,30,45,10] #每个饼块的比例
explode = (0,0.1,0,0) #第二块突出

plt.pie(sizes,explode=explode,labels=labels,autopct='%1.1f%%',pctdistance=0.7,shadow=False,startangle=90)
plt.axis('equal') #饼图成圆形
plt.legend(loc=(0.8,0.8)) #显示图例
plt.savefig('pie.png',dpi=600,bbox_inches='tight') #保存图片
plt.show() #展示图片

在这里插入图片描述

直方图的绘制

plt.hist()参数分析：

import matplotlib.pyplot as plt

plt.hist(x, bins=None, range=None, density=None, weights=None, cumulative=False, bottom=None, histtype='bar', align='mid', orientation='vertical', rwidth=None, log=False, color=None, label=None, stacked=False, normed=None, *, data=None, **kwargs)

x：数组或（允许长度不等的）数组序列
bins：整数值或序列。如果bins为整数值，则bins为柱子个数，根据数据的取值范围和柱子个数bins计算每个柱子的范围值，柱宽=(x.max()-x.min())/bins。如果bins取值为序列，则该序列给出每个柱子的范围值（即边缘）。除最后一个柱子外，其他柱子的取值范围均为半开（左闭右开）。
density：布尔值。如果为true，则返回的元组的第一个参数frequency将为频率而非默认的频数。可自行验证sum(frequency)。
weights：与x形状相同的权重数组。将x中的每个元素乘以对应权重值再计数。如果normed或density取值为True，则会对权重进行归一化处理。这个参数可用于绘制已合并的数据的直方图。
cumulative：布尔值。如果为True，则计算累计频数。如果normed或density取值为True，则计算累计频率。
bottom：数组，标量值或None。每个柱子底部相对于y=0的位置。如果是标量值，则每个柱子相对于y=0向上/向下的偏移量相同。如果是数组，则根据数组元素取值移动对应的柱子。
histtype：{‘bar’, ‘barstacked’, ‘step’, ‘stepfilled’}。'bar’是传统的条形直方图； 'barstacked’是堆叠的条形直方图；‘step’是未填充的条形直方图，只有外边框； ‘stepfilled’ 是有填充的直方图。当histtype取值为’step’或’stepfilled’，rwidth设置失效，即不能指定柱子之间的间隔，默认连接在一起。
align：{‘left’, ‘mid’, ‘right’}。‘left’：柱子的中心位于bins的左边缘；‘mid’：柱子位于bins左右边缘之间；‘right’：柱子的中心位于bins的右边缘。
orientation：{‘horizontal’, ‘vertical’}：如果取值为horizontal，则条形图将以y轴为基线，水平排列。
rwidth：标量值或None。柱子的宽度占bins宽的比例。
color：具体颜色，数组（元素为颜色）或None。有facecolor，edgecolor
label：字符串（序列）或None。有多个数据集时，用label参数做标注区分。
stacked：布尔值。如果取值为True，则输出的图为多个数据集堆叠累计的结果；如果取值为False且histtype=‘bar’或’step’，则多个数据集的柱子并排排列
normed：布尔值。官方不推荐使用，建议改用density参数。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0) #随机数种子
mu,sigma = 100,20 #均值和标准差
a = np.random.normal(mu,sigma,size=100) #产生具有正态分布的数组

plt.hist(a,20,density=1,histtype='bar',facecolor='blue',edgecolor='black',alpha=0.7)
plt.title('Histogram') #直方图标题
plt.savefig('hist.png',dpi=600,bbox_inches='tight') #保存图片
plt.show() #展示图片

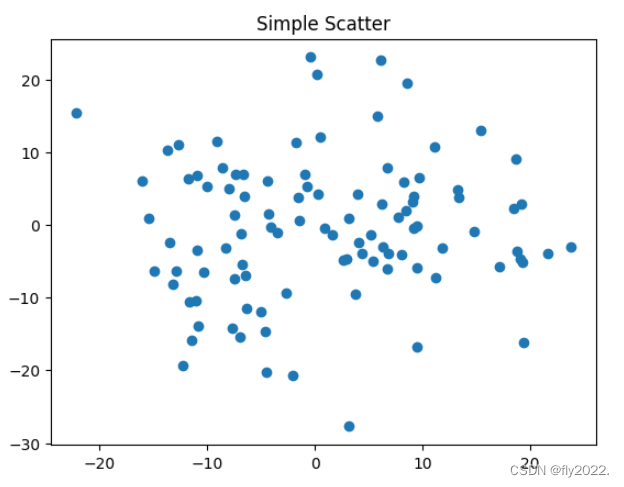
在这里插入图片描述

散点图的绘制

import numpy as np
import matplotlib.pyplot as plt

fig,ax = plt.subplots() #面向对象绘制
ax.plot(10*np.random.randn(100),10*np.random.randn(100),'o')
ax.set_title('Simple Scatter')
    
plt.savefig('散点图.png',dpi=600,bbox_inches='tight') #保存图片    
plt.show() #展示图片