大家好，我是纪宁。
在高中时，曾有一位故友问过我类似这种移盘子的题目（数列），我当时一脸茫然，上了大学才知道原来是著名的汉诺塔问题
本文，就将介绍汉诺问题的由来、原理、及C语言如何实现
目录
- 什么是汉诺塔？
- 汉诺塔原理及过程解释
- C语言代码实现
-
什么是汉诺塔？
问题背景：
主神大梵天造了三座大塔，在一个塔上从下往上按照大小顺序垒着64片圆盘。大梵天命令婆罗门借助一座塔把圆盘从下面开始按大小顺序重新摆放在另一座塔上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。如果移动一次圆盘需要1s时间，一共得用多长时间？并给出具体方法。
婆罗门不知道看到题后在想什么，哈哈
问题解释：
- 一次只能移动一张金片；
- 每次移动都只能把金片塔顶层的圆盘拿走并放在另一个塔最上面
- 移动中不能出现较小的金片在较大的金片下方的情况
-
汉诺塔原理及过程解释
假设现在就有三个圆盘，汉诺塔问题是如何进行的
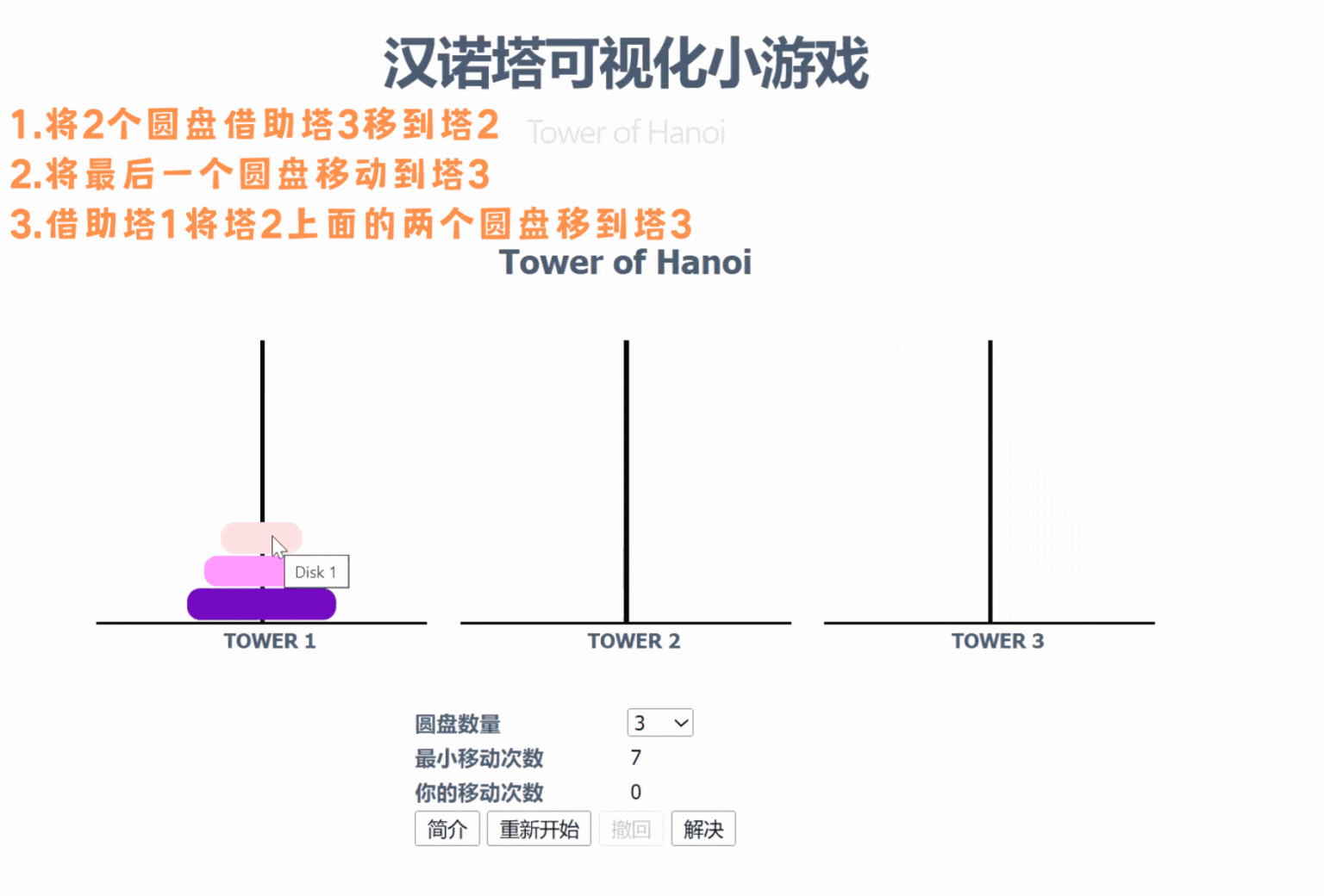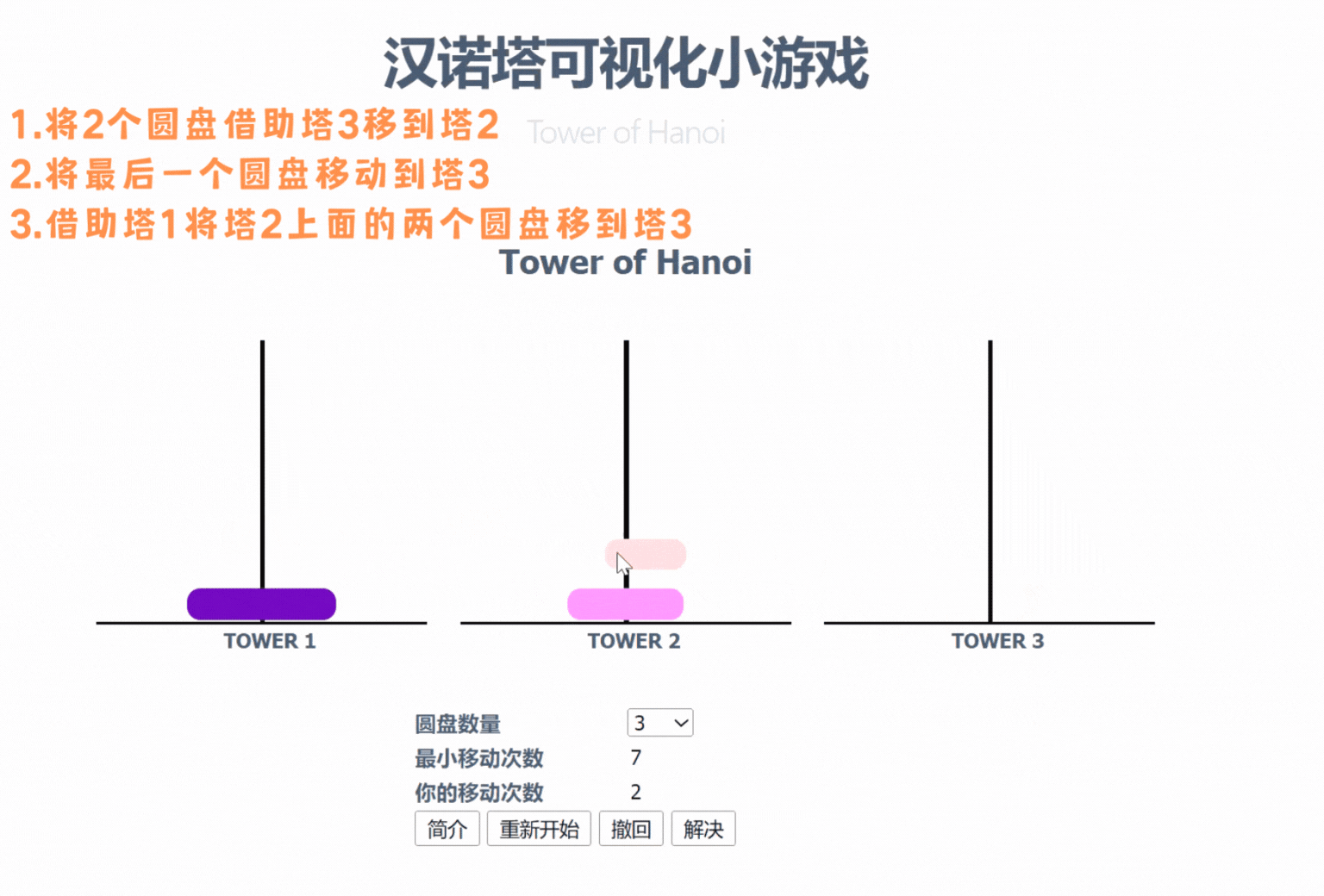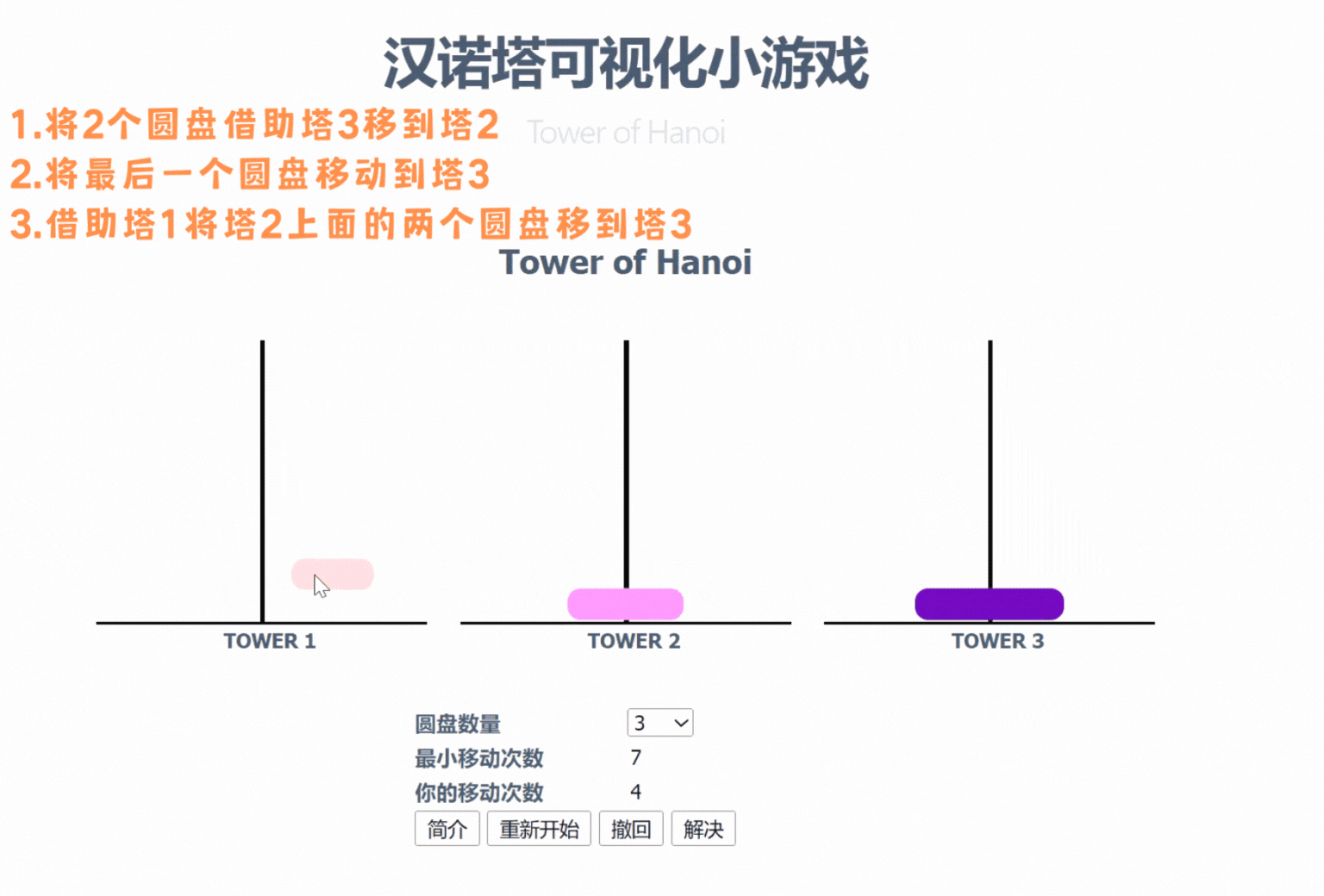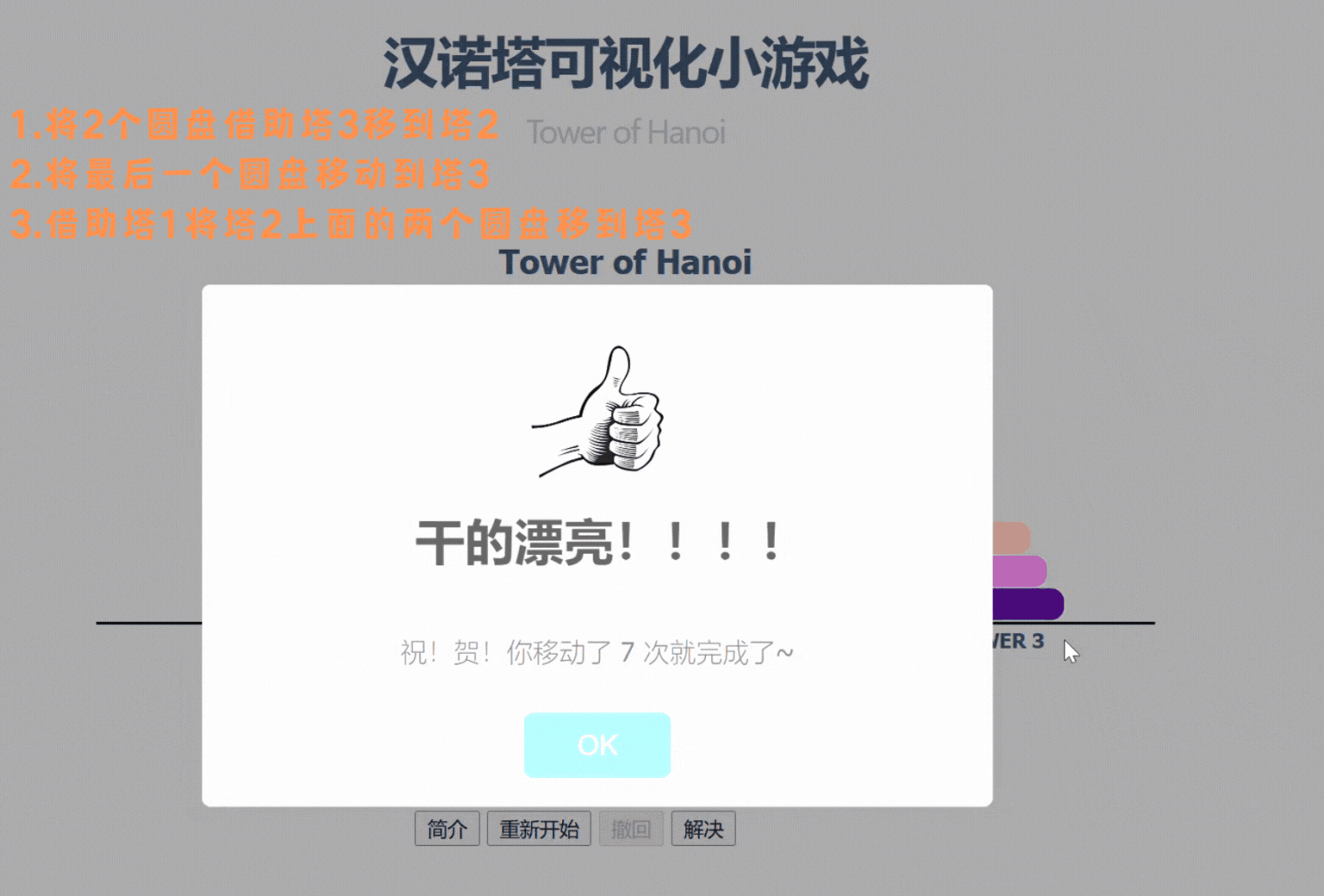
1个圆盘最小移动次数是1次（直接将圆盘从塔1移动到塔3）
2个圆盘最小移动次数是3次（先将塔1最上面的圆盘移动至塔2，再将塔1剩下的一个圆盘移动至塔3，最后将塔2上的圆盘移动至塔3）
3个圆盘最小移动次数是7次（在上图，具体过程可看上图）
由此总结：n个圆盘从塔1移动到塔3需要 （2^n-1 ）次
64个圆盘，假设婆罗门每次都移动正确，都需要（2^64-1）s，换算后大约是5859亿年才能移完。不知道大冤种婆罗门是如何做的
那么如何理解这个问题呢？
上图中，当有三个圆盘的时候，是先将借助塔3将两个圆盘移动到塔2上，再将最后一个圆盘移动到塔3，最后借助塔1将塔2的两个圆盘移动到塔3
那我们就可以总结规律：
当有n个圆盘的时候，我们可以先将（n-1）个圆盘移动到塔2上面，然后再将塔1的最后一个圆盘移至塔3，再用同样的方法将那（n-1）个元素移至塔3
过程逐步分析：
当n=1时，直接将圆盘从塔1移至塔3
当n=2时，先将第一个圆盘移至塔2，再将第二个圆盘移至塔3，最后将塔2上的一个圆盘移至塔3
当n=3时，先经塔3将前两个圆盘移至塔2，再将第三个圆盘移至塔3，最后将塔2上面的两个圆盘经塔1移至塔3
当n=4时，先经塔3将前三个圆盘移至塔2：经塔2将前两个圆盘移至塔3，再将塔1上第三个圆盘移至塔2，然后经塔1将塔2上的两个圆盘移至塔2，现在塔2上面就有了三个圆盘。将塔1上最后一个圆盘移至塔3，然后按照上面的过程类比将塔2上的三个圆盘经塔1过渡移至塔3
那就是说：当需要移动n个圆盘的时候，当n>1时候，要先将（n-1）个圆盘移至过渡塔（塔2），再将最后一个圆盘移至目标塔（塔3），最后将这（n-1）个圆盘经再移至目标塔（塔3）；当要移动（n-1）个圆盘至塔2的时候，如果（n-1）仍大于1，就要先将（n-2）个圆盘移至过渡塔（塔3），再将最后一个圆盘移至目标塔（塔2），最后将这（n-2）个圆盘再移至目标塔（塔2）......
注意：每次递归的过渡塔和终止塔都可能不同
这明显用到了递归的思想，且每次递归的终止条件是n==1
当n==1时，只需要将初始塔上面的圆盘放至终止塔即可，如果现在进行的是将塔3上面的n-2个圆盘移至塔2的话，塔3就是初始塔，塔2就是终止塔
-
C语言代码实现
#include<stdio.h>
int count = 0;//全局变量做计数器
void move(char Tower_1, char Tower_2)
{
printf("将 %c 移动到 %c \n", Tower_1, Tower_2);
count++;
}
void Hanoi(int n, char Tower_1, char Tower_2, char Tower_3)
{
if (n == 1)
//是一个的话就直接从Tower_1移动到Tower_3
move(Tower_1, Tower_3);
else
{
//不是一个的话先借助Tower_3将Tower_1上面的n-1个移动到Tower_2
Hanoi(n - 1, Tower_1, Tower_3, Tower_2);
//完成此过程后Tower_1上面还有最后一个
move(Tower_1, Tower_3); //将Tower_1上面的最后一个移动到Tower_3
//将Tower_2上面的n-1个通过Tower_1移动到Tower_3
Hanoi(n - 1, Tower_2, Tower_1, Tower_3);
}
}
int main()
{
printf("请输入圆盘个数:\n");
int n = 0;
scanf("%d", &n);
Hanoi(n, 'A', 'B', 'C');
printf("一共进行了%d次", count);
return 0;
}
博主也一直在学习过程中，有问题希望大佬指出，也欢迎大家在评论区讨论
这篇文章对你有帮助的话，希望能给博主一个免费的赞，评论和收藏
你的三连就是我更新的动力
本文收录于C语言学习专题
