(横向刷题)【算法1-6】二分查找与二分答案【算法2-1】前缀和、差分与离散化（上），总结

news2024/11/26 21:40:00

【算法1-6】二分查找与二分答案

P1024[NOIP2001 提高组] 一元三次方程求解


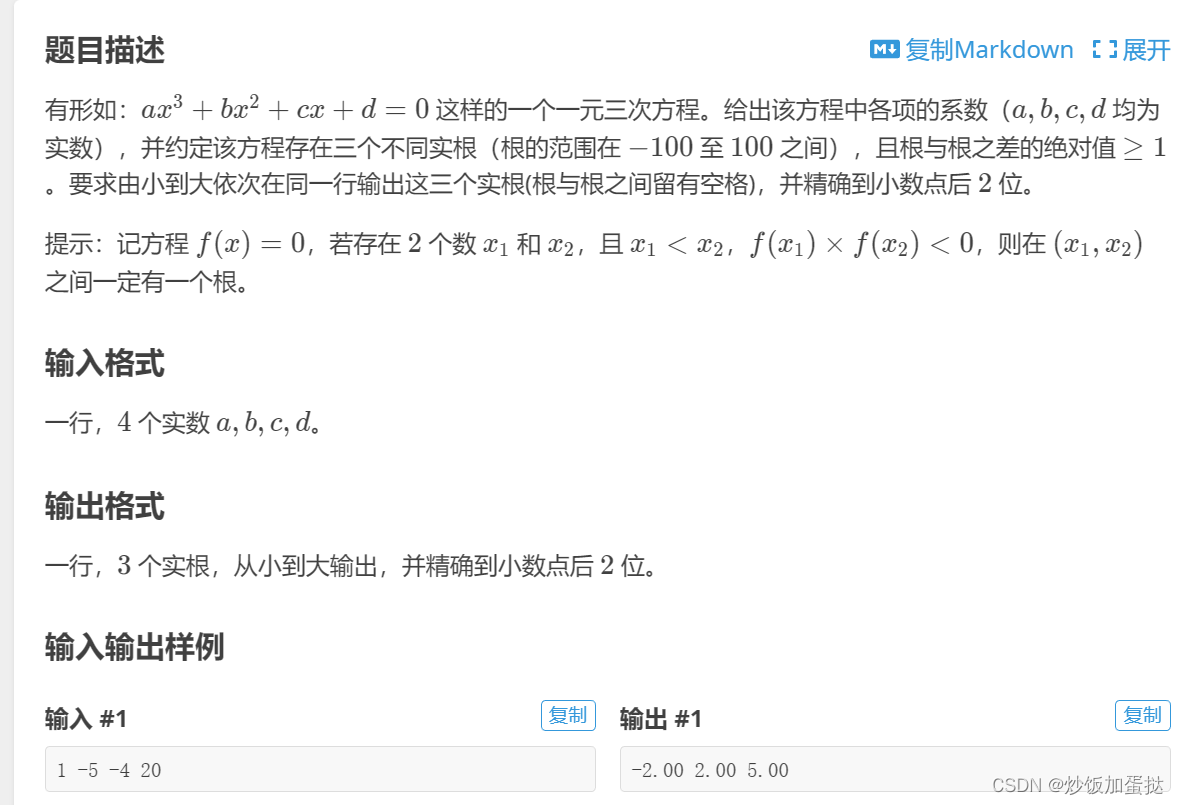
思路：题目说明根与根之差的绝对值>=1,且x1<x2&&f(x1)*f(x2)<0则其中存在解，于是联想到枚举，再用二分答案法控制精度
总结：二分对于精度的控制可以记录一下
扩展：盛金公式求解一元三次函数，记住公式模板即可，推导太过麻烦了，

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast) 
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO  cout<<"NO"<<'\n';
#define endl cout<<'\n';
typedef long long ll;
const ll maxn=2e5+10,inf = 1e18 ; 
const ll mod = 1e9 + 7;
using namespace std;
double a, b, c, d;
double check(double x) {
    return a * x * x * x + b * x * x + c * x + d;
}
 void solve(){
     cin >> a >> b >> c >> d;
     double x1, x2,l,r,m;
     int count = 0;
     for (double i = -100; i <= 100; i++) {
          l = i;
          r = i + 1;
         x1 = check(l);
         x2 = check(r);
         if (x1 == 0) {
             printf("%.2lf ", l);     //不考虑左端点，防止重复计算
             count++;
         }
         if (x1 * x2 < 0) {                            //区间内有根。
             while (r - l >= 0.001)  {                   //二分控制精度。
                 m = (l + r) / 2;
                 if (check(m) * check(r) <= 0)
                     l = m;
                 else
                     r = m;  
             }
             printf("%.2lf ", r);
             //输出右端点。
             count++;
         }
         if (count >= 3) {
             break;
         }
     }
 }
signed main()
{
    ios::sync_with_stdio(false);
    int t=1;
    //cin >> t;
    while (t--) {
        solve();
    }
}


盛金公式：
 

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast) 
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO  cout<<"NO"<<'\n';
#define endl cout<<'\n';
typedef long long ll;
const ll maxn=2e5+10,inf = 1e18 ; 
const ll mod = 1e9 + 7;
using namespace std;
int a[maxn];
vector<double>X123;
void ShengJin(double a, double b, double c, double d){
    double A = b * b - 3 * a * c;
    double B = b * c - 9 * a * d;
    double C = c * c - 3 * b * d;
    double f = B * B - 4 * A * C;
    double i_value;
    double Y1, Y2;
    if (fabs(A) < 1e-6 && fabs(B) < 1e-6)//公式1
    {
        X123.push_back(-b / (3 * a));
        X123.push_back(-b / (3 * a));
        X123.push_back(-b / (3 * a));
    }
    else if (fabs(f) < 1e-6)   //公式3
    {
        double K = B / A;
        X123.push_back(-b / a + K);
        X123.push_back(-K / 2);
        X123.push_back(-K / 2);
    }
    else if (f > 1e-6)      //公式2
    {
        Y1 = A * b + 3 * a * (-B + sqrt(f)) / 2;
        Y2 = A * b + 3 * a * (-B - sqrt(f)) / 2;
        double Y1_value = (Y1 / fabs(Y1)) * pow((double)fabs(Y1), 1.0 / 3);
        double Y2_value = (Y2 / fabs(Y2)) * pow((double)fabs(Y2), 1.0 / 3);
        X123.push_back((-b - Y1_value - Y2_value) / (3 * a));//虚根我不要
        //虚根还是看看吧，如果虚根的i小于0.1，则判定为方程的一根吧。。。
        i_value = sqrt(3.0) / 2 * (Y1_value - Y2_value) / (3 * a);
        if (fabs(i_value) < 1e-1)
        {
            X123.push_back((-b + 0.5 * (Y1_value + Y2_value)) / (3 * a));
        }
    }
    else if (f < -1e-6)   //公式4
    {
        double T = (2 * A * b - 3 * a * B) / (2 * A * sqrt(A));
        double S = acos(T);
        X123.push_back((-b - 2 * sqrt(A) * cos(S / 3)) / (3 * a));
        X123.push_back((-b + sqrt(A) * (cos(S / 3) + sqrt(3.0) * sin(S / 3))) / (3 * a));
        X123.push_back((-b + sqrt(A) * (cos(S / 3) - sqrt(3.0) * sin(S / 3))) / (3 * a));
    }
}
 void solve(){
     double a, b, c, d;
     cin >> a >> b >> c >> d;
     ShengJin(a, b, c, d);
     sort(X123.begin(), X123.end());
     for (auto i : X123) {
         printf("%.2lf ", i);
     }
 }
signed main()
{
    ios::sync_with_stdio(false);
    int t=1;
    //in >> t;
    while (t--) {
        solve();
    }
}

P1182 数列分段 Section II


思路：关键字眼最大值的最小化联想二分，直接二分最大值，l应取数组最大值，r应取数组和，
总结：这道题启发挺大，总结出二分的套路，最大值的最小化，最小值的最大化一般联想到二分，在范围内直接二分(最大值，最小值)
同时二分板子的l,r一定要写清楚，不然要调好久，并且二分的l,r并不是简单的l=0或1，r=无穷，应该考虑极端情况设想就像这题
此类问题check()函数的判定一般根据给定的划分个数

#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO  cout<<"NO"<<'\n';
#define endl cout<<'\n';
#define int long long
typedef long long ll;
const ll maxn=2e5+10,inf = 1e18 ; 
const ll mod = 1e9 + 7;
using namespace std;
int a[maxn];
int n, m;
bool check(int x) {
    ll sum = 0;
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        if (sum + a[i] <= x) {
            sum += a[i];
        }
        else {
            cnt++;
            sum = a[i];
        }
    }
    return cnt >= m;
}
 void solve(){
     cin >> n >> m;
     int l=0,r=0;
     for (int i = 1; i <=n; i++) {
         cin >> a[i];
         l = max(l, a[i]);
         r += a[i];
     }
     while (l <= r) {                 //二分板子
         int mid=(l + r) / 2;
         if (check(mid)) {
             l = mid+1 ;
         }
         else {
             r = mid - 1;
         }
     }
     cout << l << '\n';
 }
signed main()
{
    ios::sync_with_stdio(false);
    int t=1;
    //cin >> t;
    while (t--) {
        solve();
    }
}


扩展：最小值的最大化(二分)
POJ2456

题意：英文题写下题意：有n个牛栏，m头牛，然牛住进牛栏，使住牛的相邻牛栏最小间隔最大
思路：根据上题，直接二分(最小值)，范围l=0(同住一个栏)，r=(数组最大值-最小值)

#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO  cout<<"NO"<<'\n';
#define endl cout<<'\n';
typedef long long ll;
const ll maxn=2e5+10,inf = 1e18 ; 
const ll mod = 1e9 + 7;
using namespace std;
int a[maxn];
int n, m;
bool check(int x) {
    int pre = 1;
    int cnt = 1;
    for (int i = 2; i <= n; i++) {
        if ((a[i] - a[pre])>=x) {
            cnt++;
            pre = i;
            if (cnt >= m)
                return true;
        }
    }
    return false;
}
 void solve(){
     int l = 0, r = 0;
     cin >> n >> m;
     for (int i = 1; i <= n; i++) {
         cin >> a[i];
     }
     sort(a + 1, a + 1 + n);    //使之具有单调性
     r = a[n] - a[1];
     while (l < r) {
         int mid = (l+r+1) >> 1;
         if (check(mid)) {
             l = mid;
         }
         else {
             r = mid-1;
         }
     }
     cout << l << '\n';
 }
signed main()
{
    ios::sync_with_stdio(false);
    int t=1;
    //cin >> t;
    while (t--) {
        solve();
    }
}


扩展：
P3853[TJOI2007]路标设置


思路：关键字相邻路标的最大距离的最小值，直接二分最小值，套板子，check的判定在距离内本就有两个路标，若有余数说明需要y/x向下取整的路标数，但没余数则多出一个

#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO  cout<<"NO"<<'\n';
#define endl cout<<'\n';
typedef long long ll;
const ll maxn=2e5+10,inf = 1e18 ; 
const ll mod = 1e9 + 7;
using namespace std;
int a[maxn];
int L, n, k;
bool check(int x) {
    int cnt = 0;
    for (int i = 2; i <= n; i++) {
        int y = a[i] - a[i - 1];
        if (y > x) {
            cnt += (y)/x;
            if (y % x == 0) {
                cnt--;
            }
        }
    }
    return cnt <= k;
}
 void solve(){
     cin >> L >> n >> k;
     for (int i = 1; i <= n; i++) {
         cin >> a[i];
     }
     int l = 1, r = L;
     while (l <= r) {
         int mid = (l + r) >> 1;
         if (check(mid)) {
             r = mid-1;
             
         }
         else {
             l = mid +1;
         }
     }
     cout << l << '\n';
     
 }
signed main()
{
    ios::sync_with_stdio(false);
    int t=1;
    //cin >> t;
    while (t--) {
        solve();
    }
}

【算法2-1】前缀和、差分与离散化（上）

AcWing 802. 区间和


思路：对于操作的位置x,和查询的位置l,r值域大，个数较少，于是离散化，
之后二分映射找到离散化后的操作位置+c,前缀和处理，对于询问也同样二分映射找到离散化后的询问位置查询，
对于查询有点像离线操作,这道题在ACW
总结：在数据值域很大，但个数较少的时候,可以使用离散化，如果使用map会爆内存，
 离散化的本质还是映射，将值域间隔大的点映射到间隔数组，无论是对查询，还是操作都会节省时间和空间要求，这道题感觉很典型

#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO  cout<<"NO"<<'\n';
#define endl cout<<'\n';
typedef long long ll;
const ll maxn=2e5+10,inf = 1e18 ; 
const ll mod = 1e9 + 7;
using namespace std;
int a[maxn];
int Hash[maxn<<1];
int s[maxn];
int sum[maxn];
vector<pair<int, int>>v;   //操作
vector<pair<int, int>>v1;     //询问
 void solve(){
     int n,m;
     cin >> n>>m;
     int cnt = 0;
     for (int i = 1; i <= n; i++) {
         int x, c;
         cin >> x >> c;
         v.push_back({ x,c });    //操作离线
         Hash[++cnt] = x;   //离散
     }
     for (int i = 1; i <= m; i++) {
         int l, r;
         cin >> l >> r;
         v1.push_back({ l,r });   //查询离线
         Hash[++cnt] = l;
         Hash[++cnt] = r;
     }
     sort(Hash + 1, Hash + 1 + cnt);
     auto k = unique(Hash, Hash + 1 + cnt);
     for (auto x : v) {    //执行操作
         int y = lower_bound(Hash + 1, Hash + 1 + cnt, x.first) - Hash;  //找到离散化后的操作位置
         a[y] += x.second;
     }
     for (int i = 1; i <= cnt; i++) {
         a[i] += a[i - 1];
     }
     for (auto x : v1) {
         int l= lower_bound(Hash + 1, Hash + 1 + cnt, x.first) - Hash;  
         int r = lower_bound(Hash + 1, Hash + 1 + cnt, x.second) - Hash;
         cout << a[r] - a[l - 1] << '\n';
     }

 }
signed main()
{
    ios::sync_with_stdio(false);
    int t=1;
    //cin >> t;
    while (t--) {
        solve();
    }
}


扩展：P1496 火烧赤壁


思路：同样是数据值域很大，但个数较少，于是离散化，在离散化后的数组操作，同上，一定注意左开右闭，像我没注意到调了好久
总结：离散化的套路很明显，数据值域很大，但个数较少，把原数组操作转化到离散数组的操作，映射即可

#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO  cout<<"NO"<<'\n';
#define endl cout<<'\n';
#define int long long
typedef long long ll;
const ll maxn = 2e5 + 10, inf = 1e18;
const ll mod = 1e9 + 7;
using namespace std;
int Hash[maxn << 1];
vector<pair<int, int>>v;   //操作
int flag[maxn];
void solve() {
    int n;
    cin >> n;
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        int l, r;
        cin >> l >> r;
        v.push_back({ l,r });   //操作离线
        Hash[++cnt] = l;
        Hash[++cnt] = r;
    }
    cnt++;
    sort(Hash + 1, Hash + 1 + cnt);
    for (auto x : v) {    //执行操作
        int l = lower_bound(Hash + 1, Hash + 1 + cnt, x.first) - Hash;  //找到离散化后的操作位置
        int r = lower_bound(Hash + 1, Hash + 1 + cnt, x.second) - Hash;  
        for (int i = l; i <= r-1; i++) {     //左闭右开
            flag[i]++;
        }
    }
    int ans = 0;
    for (int i = 1; i <= cnt; i++) {
        if (flag[i]) {
            ans += Hash[i + 1] - Hash[i];
        }
    }
    cout << ans << '\n';
}
signed main()
{
    ios::sync_with_stdio(false);
    int t = 1;
    //cin >> t;
    while (t--) {
        solve();
    }
}


P1955[NOI2015] 程序自动分析


思路：同样注意到i,j值域很大，但个数较小，离散化，判定满不满足条件，可以并查集判定,这道题还是挺简单的
总结：通过前几个题目可以发现，把原数组操作转化到离散数组的操作，操作是离线的

#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<cstring>
#include<math.h>
#include<map>
#include<vector>
#include<stack>
#define ms(x,y) memset(x,y,sizeof x);
#define YES cout<<"YES"<<'\n';
#define NO  cout<<"NO"<<'\n';
#define endl cout<<'\n';
typedef long long ll;
const ll maxn=2e6+10,inf = 1e18 ; 
const ll mod = 1e9 + 7;
using namespace std;
int t, n, f[maxn], Hash[maxn];  
struct node {
    int x, y, e;
}a[maxn];
bool cmp(node a, node b) {
    return a.e > b.e;
}
int find(int x) {
    return f[x] == x ? x : f[x] = find(f[x]); 
} //并查集
void solve(){
    int cnt = 0;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i].x >> a[i].y >> a[i].e;
        Hash[++cnt] = a[i].x;
        Hash[++cnt] = a[i].y;
    }
    sort(Hash, Hash + cnt);//排序 
    int len = unique(Hash, Hash + cnt) - Hash-1;  //去重 
    for (int i = 1; i <= n; ++i) {
        a[i].x = lower_bound(Hash, Hash + len, a[i].x) - Hash;
        a[i].y = lower_bound(Hash, Hash + len, a[i].y) - Hash;
    }
    for (int i = 1; i <= len; ++i) {
        f[i] = i;
    }
    sort(a + 1, a + n + 1, cmp);  //按e排序 
    for (int i = 1; i <= n; i++) {
        int r1 = find(a[i].x);
        int r2 = find(a[i].y);
        if (a[i].e) {
            f[r1] = r2; 
        }
        else if (r1 == r2) {
            NO;
            return;
        }
    }
    YES;
}
int main() {
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

这周任务安排

除cf,牛客重现赛补题，坚持对以前的算法，数据结构进行横向刷题，这周为【算法2-1】前缀和、差分与离散化（上），【算法2-3】分治与倍增

总结

通过对以前的算法进行巩固，发现了许多套路，像二分的最大值的最小化，最小值的最大化，离散的数据值域很大，但个数较少，这都是以前没有发现的，还有对题目的总结，扩展也很重要，做题的时候切忌浮躁，一定好好好琢磨背后考察的知识点，另外就是与师傅的沟通不够

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/647271.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【RabbitMQ教程】第四章 —— RabbitMQ - 交换机

【RabbitMQ教程】第四章 —— RabbitMQ - 交换机

&#x1f4a7; 【 R a b b i t M Q 教程】第四章—— R a b b i t M Q − 交换机 \color{#FF1493}{【RabbitMQ教程】第四章 —— RabbitMQ - 交换机} 【RabbitMQ教程】第四章——RabbitMQ−交换机&#x1f4a7; &#x1f337; 仰望天空&#xff0c;妳我亦是行人.✨ &…
阅读更多...
《阿里大数据之路》读书笔记：第一章 总述

《阿里大数据之路》读书笔记：第一章 总述

阿里巴巴大数据系统体系架构图 阿里数据体系主要分为数据采集、数据计算、数据服务和数据应用四大层次。 一、数据采集层 阿里巴巴建立了一套标准的数据采集体系方案&#xff0c;致力全面、高性能、规范地完成海量数据的采集&#xff0c;并将其传输到大数据平台。 数据来源主…
阅读更多...
【C++】 STL（下）算法、迭代器、容器适配器 和 仿函数

【C++】 STL（下）算法、迭代器、容器适配器 和 仿函数

文章目录 算法迭代器容器适配器栈&#xff08;stack&#xff09;队列&#xff08;queue&#xff09; 仿函数 算法 STL中的算法头文件位于和文件中&#xff08;以为主&#xff09; for_each(InputIterator First,InputIterator Last,Function _Func); 遍历&#xff0c;具体做什…
阅读更多...
电影《天空之城》观后感

电影《天空之城》观后感

上周看了电影《天空之城》这部电影&#xff0c;这部电影是六一儿童节时上映的&#xff0c;本周也算是补票吧&#xff0c;童年时&#xff0c;看的都是免费的&#xff0c;早已经忘记是在哪里看到的&#xff0c;但当时对自己触动很大&#xff0c;算是启蒙电影&#xff0c;所以今天…
阅读更多...
【RabbitMQ教程】第二章 —— RabbitMQ - 简单案例

【RabbitMQ教程】第二章 —— RabbitMQ - 简单案例

&#x1f4a7; 【 R a b b i t M Q 教程】第二章—— R a b b i t M Q − 简单案例 \color{#FF1493}{【RabbitMQ教程】第二章 —— RabbitMQ - 简单案例} 【RabbitMQ教程】第二章——RabbitMQ−简单案例&#x1f4a7; &#x1f337; 仰望天空&#xff0c;妳我亦是行人…
阅读更多...
汽车电子Autosar之以太网SOMEIP

汽车电子Autosar之以太网SOMEIP

前言 首先&#xff0c;请问大家几个小小问题&#xff0c;你清楚&#xff1a; 你知道什么是SOME/IP吗&#xff1f;你知道为什么会产生SOME/IP即相关背景吗&#xff1f;你知道SOME/IP与SOA又有着哪些千丝万缕的联系呢&#xff1f;SOME/IP在实践中到底应该如何使用呢&#xff1f…
阅读更多...
QuickList

QuickList

基本概述 ZipList虽节省内存但是申请内存必须是连续的&#xff0c;如果内存占用很大&#xff0c;申请内存效率就会很低&#xff0c;可以限制ZipList长度和entry大小&#xff1b; 实在要存储大量数据&#xff0c;超出ZipList最佳上限了&#xff0c;此时可以创建多个ZipList来分片…
阅读更多...
Autosar诊断实战系列04-基于CAPL语言的通信类诊断测试脚本开发

Autosar诊断实战系列04-基于CAPL语言的通信类诊断测试脚本开发

本文框架 前言1.CAPL编程简单介绍2. CAPL脚本开发实战2.1 添加CAPL Test Module2.2 CAPL脚本实战编写前言 在本系列笔者将结合工作中对诊断实战部分的应用经验进一步介绍常用UDS服务的进一步探讨及开发中注意事项， Dem/Dcm/CanTp/Fim模块配置开发及注意事项，诊断与BswM/NvM关…
阅读更多...
OpenAI官方提示词课（五）如何进行文本翻译校正修改

OpenAI官方提示词课（五）如何进行文本翻译校正修改

在本篇文章中&#xff0c;我们将探讨如何使用大语言模型进行文本转换任务&#xff0c;例如语言翻译、拼写和语法检查、语气调整和格式转换。 翻译 ChatGPT接受多种语言的训练&#xff0c;使得模型具备翻译能力。以下是如何使用这种能力的一些示例。 prompt f""&q…
阅读更多...
利用lambda优化反射功能实现方法调用

利用lambda优化反射功能实现方法调用

最近在思考lambda相关的问题&#xff0c;简单记录下做的相关反射替代和函数映射的尝试。 原理分析 lambda是jdk8才提供的&#xff0c;原理其实就是动态生成内部类来执行函数映射的方法。也就是说一段lambda表达式会对应特定的类方法&#xff0c;之后调用。底层是通过LambdaMe…
阅读更多...
《离散数学》：逻辑

《离散数学》：逻辑

〇、前言 离散数学是数学的一个分支&#xff0c;研究离散对象和离散结构的数学理论和方法。这学期学校开了离散数学的课程&#xff0c;我受益颇丰&#xff0c;感觉到了离散数学真正的魅力&#xff0c;也被开创离散数学各个分支的人的聪明与才智深深折服。与连续数学不同&#…
阅读更多...
Stopwatch工具类计时器探究

Stopwatch工具类计时器探究

搬砖的我们 特别是Java开发的童鞋们, 经常需要通过记录开始时间和结束时间&#xff0c;然后通过计算差值&#xff0c;得到时间差&#xff0c;如下面的代码&#xff1a; long start System.currentTimeMillis(); long end System.currentTimeMillis(); System.out.println(…
阅读更多...
【数字调制】数字调制技术FSK与PSK分析与研究(Matlab代码实现）

【数字调制】数字调制技术FSK与PSK分析与研究(Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
栈的数据结构完成表达式（5*10+2-7+5）/10+5的计算

栈的数据结构完成表达式（5*10+2-7+5）/10+5的计算

栈&#xff08;Stack&#xff09;是一种线性数据结构&#xff0c;具有后进先出&#xff08;LIFO&#xff09;的特性。它可以理解为一种类似于抽屉的容器&#xff0c;只能在顶部进行插入和删除操作&#xff0c;其他位置不可访问。栈的基本操作包括入栈&#xff08;push&#xff…
阅读更多...
[数字图像处理]第五章 图像复原与重建

[数字图像处理]第五章 图像复原与重建

文章目录 第五章 图像复原与重建5.1图像退化复原过程的模型图像退化图像复原图像复原与图像增强图像退化的数学模型为什么采用线性位移不变系统模型来描述图像退化过程 5.2 噪声模型x5.2.1 噪声的空间和频率特性5.2.2 一些重要的噪声概率密度函数高斯噪声实验&#xff1a;采用高…
阅读更多...
【微服务架构设计和实现】4.1 微服务架构概述和设计原则

【微服务架构设计和实现】4.1 微服务架构概述和设计原则

往期回顾&#xff1a; 第一章&#xff1a;【云原生概念和技术】 第二章&#xff1a;【容器化应用程序设计和开发】 第三章&#xff1a;【基于容器的部署、管理和扩展】 4.1 微服务架构概述和设计原则 4.1 微服务架构概述和设计原则4.1.1 微服务架构的优点4.1.2 微服务架构遵…
阅读更多...
在 ArcGIS Pro 中使用 H3 创建蜂窝六边形

在 ArcGIS Pro 中使用 H3 创建蜂窝六边形

在 ArcGIS Pro 中使用 H3 创建蜂窝六边形https://mp.weixin.qq.com/s/tGk7AT2jAcvsmNyp2bRvig 之前看了个有意思的ArcGIS博客&#xff1a;H3六边形&#xff0c;当然了这也不是个新鲜东西了。原文&#xff1a; https://www.esri.com/arcgis-blog/products/arcgis-pro/analytic…
阅读更多...
为什么要学GIS开发

为什么要学GIS开发

什么是地理信息系统技术&#xff1f; GIS技术使用专门的计算机系统来获取地理数据并将其集成到智能“超级”地图中。然后&#xff0c;这些数据可用于创建无穷无尽的“假设”场景&#xff0c;为以下应用程序提供强大的工具&#xff1a; 制图&#xff08;地图制作&#xff09;应…
阅读更多...
【阅读随笔】Rewrite-Based Decomposition of Signal Temporal Logic Specifications

【阅读随笔】Rewrite-Based Decomposition of Signal Temporal Logic Specifications

文章目录 Overview1 IntroLTL任务分解STL任务分解本文工作 Background and Problem DefinitionSTLAgent假设与问题方法 An STL Rewriting SystemRewriting SystemFormula Rewrite DAG Decomposing STL智能体编队任务分解最优分解 Exploring the Formula Rewrite DAGExperiments…
阅读更多...
soci在windows下vs2010编译

soci在windows下vs2010编译

需要下载 的资源 mysql connector c 因为其使用的的是mysql connector c的api&#xff0c;需要下载https://downloads.mysql.com/archives/c-c/ 分别对应32位和64位的 soci 4.0 从github上下载4.03分支 https://github.com/SOCI/soci/tree/v4.0.3 cmake 需要下载3.25版…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023