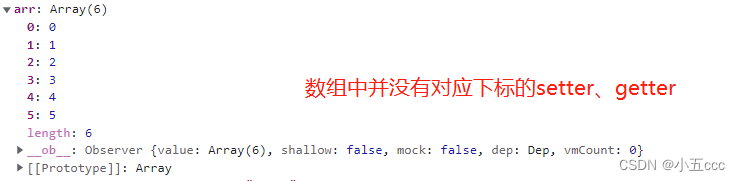
顺序表和链表同属于线性表，线性表顾名思义，就是连续的一条直线，但它在物理结构上是不一定连续的，通常的线性表用顺序表和链表来实现。下面我们介绍顺序表和链表

文章目录

1. 顺序表
- 1.1 顺序表的大致介绍
- 1.2 顺序表的代码实现
- - 顺序表的初始化
  - 顺序表的尾插
  - 顺序表的尾删
  - 顺序表的头插
  - 顺序表的头删
  - 顺序表的打印
  - 在顺序表中查找指定元素的位置
  - 在指定位置后插入
  - 删除指定位置的数据
  - 顺序表的销毁
- 1.3 顺序表的OJ题目
- - 移除元素
  - 删除有序数组中的重复项
  - 合并两个有序数组
2.链表
- 2.1 链表的大致介绍
- 2.2 单向不带头不循环链表的代码实现
- - 链表节点的创建
  - 链表的尾插
  - 链表的尾删
  - 链表的头插
  - 链表的头删
  - 链表的打印
  - 在链表中查找指定元素
  - 在链表的指定位置之前进行数据的插入
  - 在链表的指定位置之后进行数据的插入
  - 删除链表指定的节点
  - 删除链表指定位置节点之后的节点
- 2.3 双向带头循环链表的实现（最强大的链表）
- - 链表节点的创建
  - 链表的初始化
  - 链表的尾插
  - 链表的尾删
  - 链表的头插
  - 链表的头删
  - 找到链表的指定节点
  - 在链表的指定位置之前进行插入
  - 删除链表的指定位置
  - 链表的销毁
- 2.4 链表的OJ题目
- - 移除链表元素
  - 反转链表

1. 顺序表

1.1 顺序表的大致介绍

顺序表用一段物理地址联系的结构存储数据，一般情况下采用数组存储。
顺序表又分为静态顺序表和动态顺序表。
静态顺序表非常简单，就是普通的定长数组。下面我们重点讨论动态顺序表。

一个动态顺序表，即有它的指向指定数据的指针，又有它表示目前存储多少数据的变量，还有它表示总共能存储多少数据的变量。

1.2 顺序表的代码实现

我们把代码分成三个文件来写

SepList.h 在这个文件中我们写宏定义，类型的重定义以及各种接口函数的声明
SepList.c 在这个文件中我们写各种接口函数的定义
test.c 在这个文件中我们通过调用各种接口函数，从而对接口函数进行测试

下面正式开始书写代码

首先我们得把各种的准备工作做好，也就是说必须先把头文件中各种什么宏定义。重定义，函数声明给解决了

那既然是数据结构，那必然得有数据的类型吧？我们用的这个数据是类型是什么？
是char还是int？亦或是其他类型？它们都可以。所以我们创建的数据结构必须是通用的，也就是说，我们创建的这个数据结构必须要即能用于所有的变量类型。

如何实现呢？我们可以先把要使用的数据类型进行重定义，使得它具有新的名字。

typedef int SLDataType;

这样有什么好处呢？比如我们在使用int类型的变量作为这个链表中数据的数据类型，那必然在代码中大量的提到了int。如果我们要再使用char类型，那么在代码中必然要进行大量的修改。而如果使用重定义的话，我们就只需在重定义的地方将int改成char就可以了。

typedef char SLDataType;

然后我们继续创建结构体，把顺序表所有要用到的变量都封装起来，为了方便结构体的使用，我们可以也对结构体进行重定义一下。

typedef struct SepList
{
	SLDataType* a;
	int size;
	int capacity;
}SL;

接下来就是各种借口函数的声明了

// 对顺序表进行初始化
void  SepListInit(SL* ps);

// 对顺序表进行打印
void SepListPrint(SL* ps);

// 对顺序表进行销毁
void SepListDestroy(SL* ps);

// 对顺序表进行尾插
void SepListPushBack(SL* ps, SLDataType x);

// 对顺序表进行尾删
void SepListPopBack(SL* ps);

// 对顺序表进行头插
void SepListPushFront(SL* ps, SLDataType x);

// 对顺序表进行头删
void SepListPopFront(SL* ps);

// 在顺序表中查找指定元素的位置
int SepListFind(SL* ps,int pos, SLDataType x);

// 在顺序表的指定位置后面插入数据
void SepListInsert(SL* ps, int pos, SLDataType x);

// 在顺序表的指定位置删除数据
void SepListErase(SL* ps, int pos);

下面实现各种接口函数并进行测试

顺序表的初始化

在初识化时我们先不申请空间，将结构体中的指针置为空，将size和capacity置为0。
在进入函数后的第一件事就是进行断言，断言可以很容易地帮我们找出程序中的错误，后续在其他函数的实现中也是如此。

void SepListInit(SL* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->size = ps->capacity = 0;
}

顺序表的尾插

在尾插或者是在其他位置插入，我们要做的第一件事就是检查数据是否已经存满，如果已经存满，我们还需进行扩容。
扩容时，频繁扩容不太合适，但是我们扩的太多又会造成空间的浪费，这个时候最好的方法就是初次扩容扩四个空间，然后每次扩容都将空间扩两倍。

void SepListPushBack(SL* ps, SLDataType x)
{
	assert(ps);
	if (ps->size == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		SLDataType* tmp = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newCapacity;
	}
	ps->a[ps->size++] = x;
}

顺序表的尾删

尾删就比较简单了，size变量表示的是这个顺序表有多少数据，我们尾删时只需把
size这个变量减一就行了。
可能你要问要不要把那个被删除的位置的变量值为0，或是置为-1？没必要！ 我们已经不会再访问那个位置的数据了，就不用管那个位置的数据是多少了，是0还是-1，亦或者是一个随机值，都无所谓。
可能你也要问可不可以把那个删除的位置的数据给释放了，不可以！ 顺序表的空间是连续的，只可以同时全部释放，不可以分段释放，分段释放程序会报错。
这样就完成了吗？程序是否有什么错误呢？
在每次删除数据时都必须要断言顺序表是否为空，为空则不能删除！

void SepListPopBack(SL* ps)
{
	assert(ps);
	assert(ps->size > 0);
	ps->size--;
}

顺序表的头插

头插的话就比较麻烦啦，每次在顺序表的开头插入一个数据，我们都必须挪动后面数据来为它腾出位置。就好比若干个人按年龄依此从小到大坐位置，突然来了一个年龄最小的，那么已经坐好的每个人都必须移动来为它腾出位置。
那么我们要先将所有数据向后挪一个位置，然后再将这个数据放到第一个位置。
挪要怎样挪？如果从前往后挪会改变原来的数据，如图所示
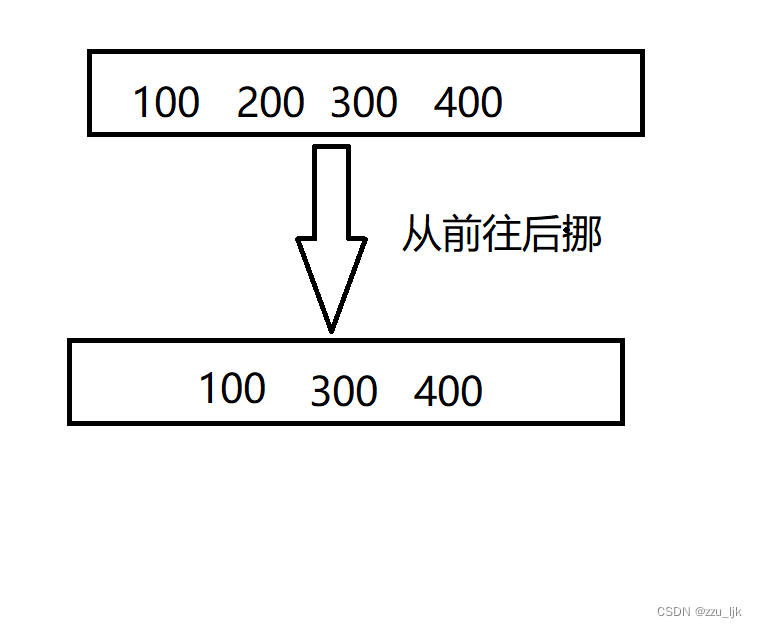
在这里插入图片描述
所以我们采用从后往前挪

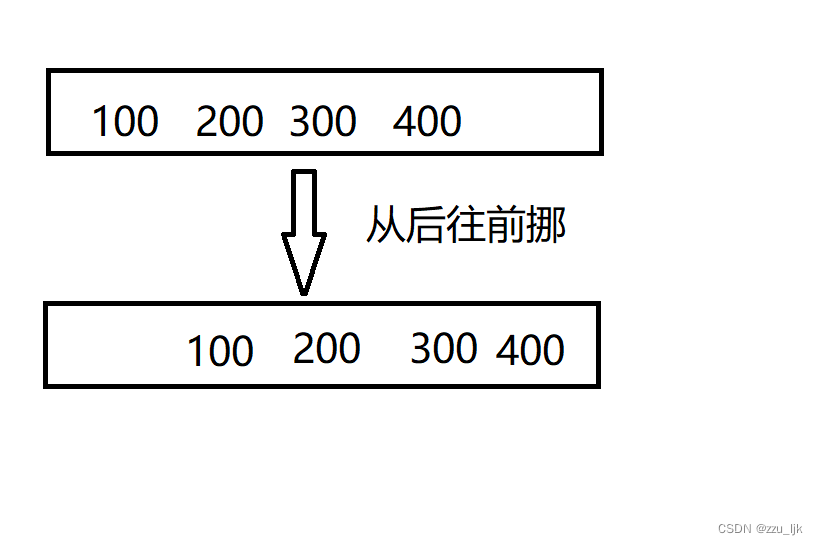
再将我们要放的数据放到第一个位置（假如放入1）
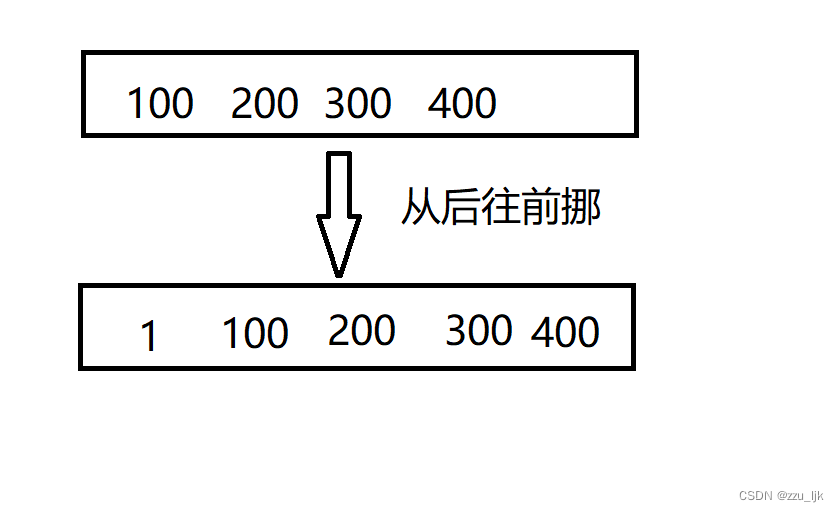
在这里插入图片描述
代码如下：

void SepListPushFront(SL* ps, SLDataType x)
{
	assert(ps);

	if (ps->size == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		SLDataType* tmp = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newCapacity;
	}
	int i = 0;
	for (i = ps->size; i > 0; i--)
		ps->a[i] = ps->a[i - 1];
	
	ps->a[0] = x;
	ps->size++;
}

每次在插入数据之前都检查是否需要扩容，显得代码有点繁琐，我们可以把检查是否需要扩容的部分用函数封装起来，在插入之前进行调用即可

void CheckCapacity(SL* ps)
{
	if (ps->size == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		SLDataType* tmp = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newCapacity;
	}
}

优化后的代码如下：

void SepListPushFront(SL* ps, SLDataType x)
{
	assert(ps);

	CheckCapacity(ps);
	
	int i = 0;
	for (i = ps->size; i > 0; i--)
		ps->a[i] = ps->a[i - 1];

	ps->a[0] = x;
	ps->size++;
}

void SepListPushBack(SL* ps, SLDataType x)
{
	assert(ps);
	
	CheckCapacity(ps);

	ps->a[ps->size++] = x;
}

怎么样，是不是变得简洁许多呢？

顺序表的头删

顺序表的头删和头插一样，都是挪动数据的问题。并且在删除之前需要断言顺序表是否为空，为空则不能删除。
那么我们看头删是从前向后挪还是从后向前挪呢？

若是从后向前挪
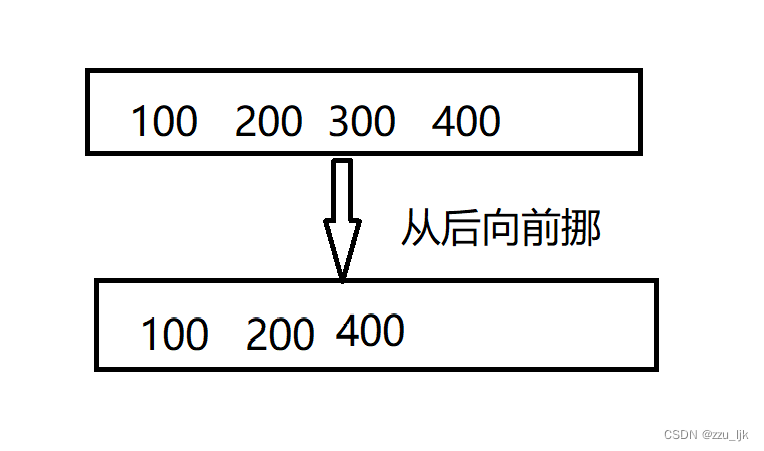
在这里插入图片描述
可以看到，刚挪第一步我们就把不该覆盖的数据覆盖掉了，所以从后向前挪是不可取的。那我们再试试从前向后挪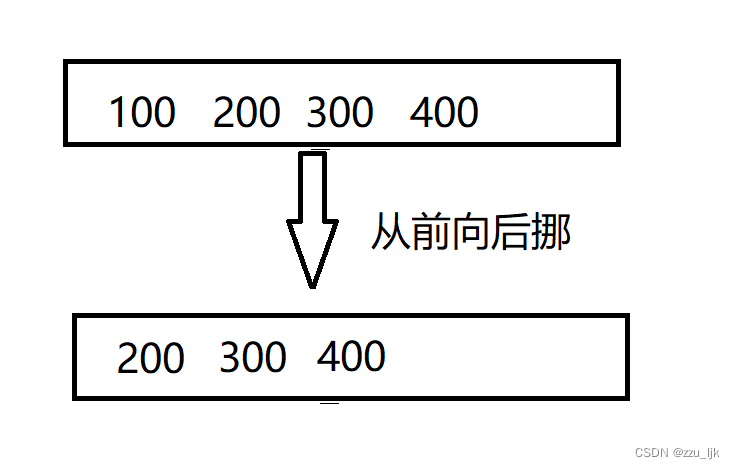
这就很舒服，所有的数据都移动到了正确的位置上。

代码如下：

void SepListPopFront(SL* ps)
{
	assert(ps);
	assert(ps->size > 0);

	int i = 0;
	for (int i = 0; i < ps->size - 1; i++)
		ps->a[i] = ps->a[i + 1];
	
	ps->size--;
}

顺序表的打印

完成了尾插尾删头插头删，我们再进行这些操作来讲顺序表打印出来，来看我们的接口函数设计的是否正确。
当然我这里的测试方法是不可取得，最好在写完一个接口函数就对这个接口函数进行测试。
顺序表打印函数的代码如下

void SepListPrint(SL* ps)
{
	assert(ps);
	int i = 0;
	for (i = 0; i < ps->size; i++)
		printf("%d ", ps->a[i]);
}

下面对以上函数进行测试
测试代码：

void test()
{
	SL sl;
	SepListInit(&sl);
	
	SepListPushBack(&sl, 100);
	SepListPushBack(&sl, 200);
	SepListPushBack(&sl, 300);
	SepListPushBack(&sl, 400);

	SepListPopBack(&sl);

	SepListPushFront(&sl, 1);
	SepListPushFront(&sl, 2);
	SepListPushFront(&sl, 3);
	SepListPushFront(&sl, 4);

	SepListPopFront(&sl);

	SepListPrint(&sl);
}

测试结果：
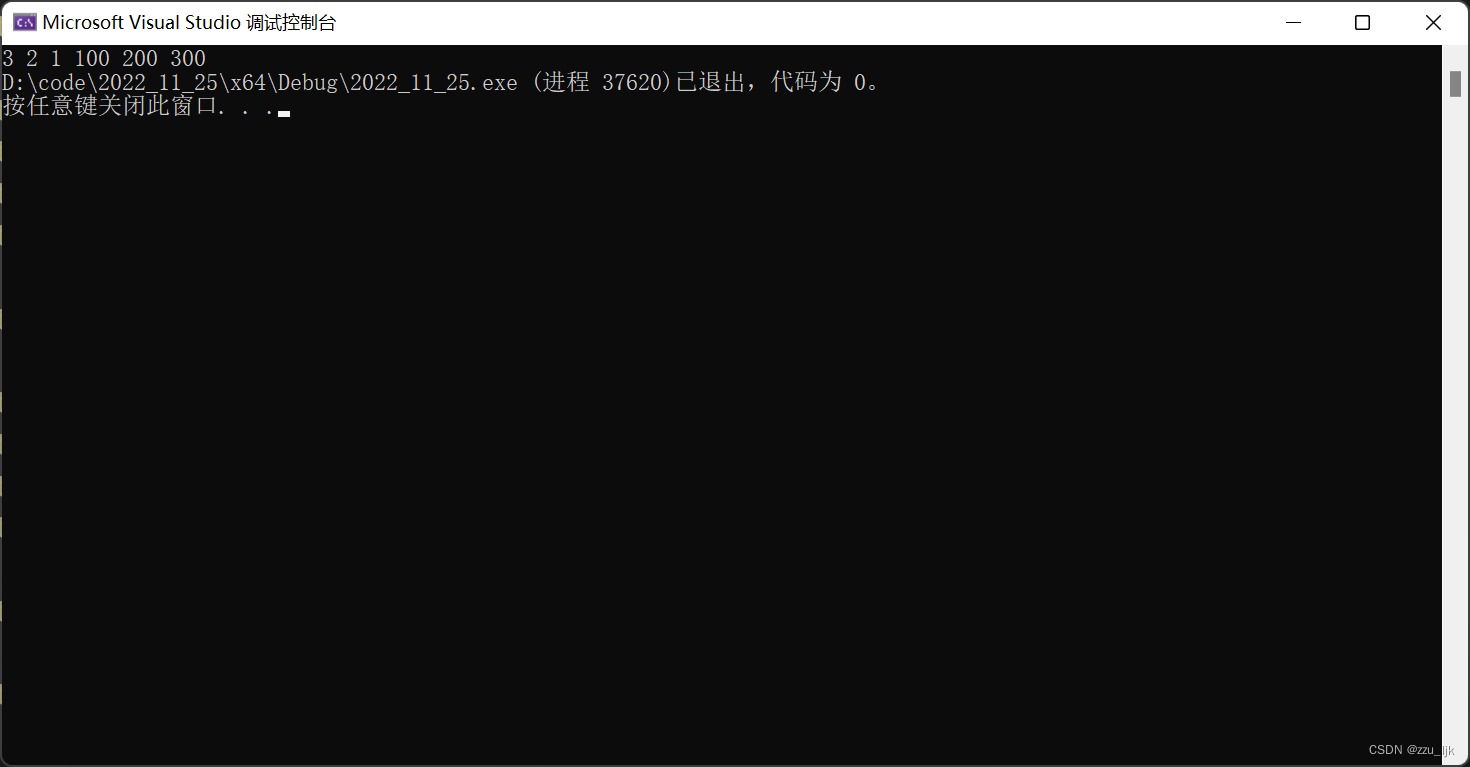
在这里插入图片描述
这里结果和我们的预期是一样的，所以我们上面的函数书写都是无误的。

在顺序表中查找指定元素的位置

我们遍历整个顺序表，看是否有我们想要的数据，如果有，返回它的下标，如果没有则返回-1。
代码如下：

int SepListFind(SL* ps, SLDataType x)
{
	assert(ps);
	int i = 0;
	for (i = 0; i < ps->size; i++)
		if (ps->a[i] == x)
			return i;

	return -1;
}

我们继续看，这个代码是否有一定缺陷呢？
比如我要查找整数1，那么如果这个顺序表中有多个整数1，就只能找到最前面那个整数1的下标了。
如果非要对这个缺陷进行改进，只需在该函数的参数表中多加入一个参数，该参数表示从哪个下标开始遍历。

int SepListFind(SL* ps, int pos, SLDataType x)
{
	assert(ps);
	int i = 0;
	for (i = pos; i < ps->size; i++)
		if (ps->a[i] == x)
			return i;

	return -1;
}

然后我们对这个函数进行测试，在顺序表中设置多个100，并打印这多个100的下标。
测试代码如下：

void test2()
{
	SL sl;
	SepListInit(&sl);

	SepListPushBack(&sl, 100);
	SepListPushBack(&sl, 100);
	SepListPushBack(&sl, 100);
	SepListPushBack(&sl, 100);
	SepListPushBack(&sl, 100);


	int pos = SepListFind(&sl, 0, 100);
	while (pos < sl.size && pos >= 0)
	{
		printf("%d ", pos);
		pos = SepListFind(&sl, pos + 1, 100);
	}
}

我们运行程序，查看结果
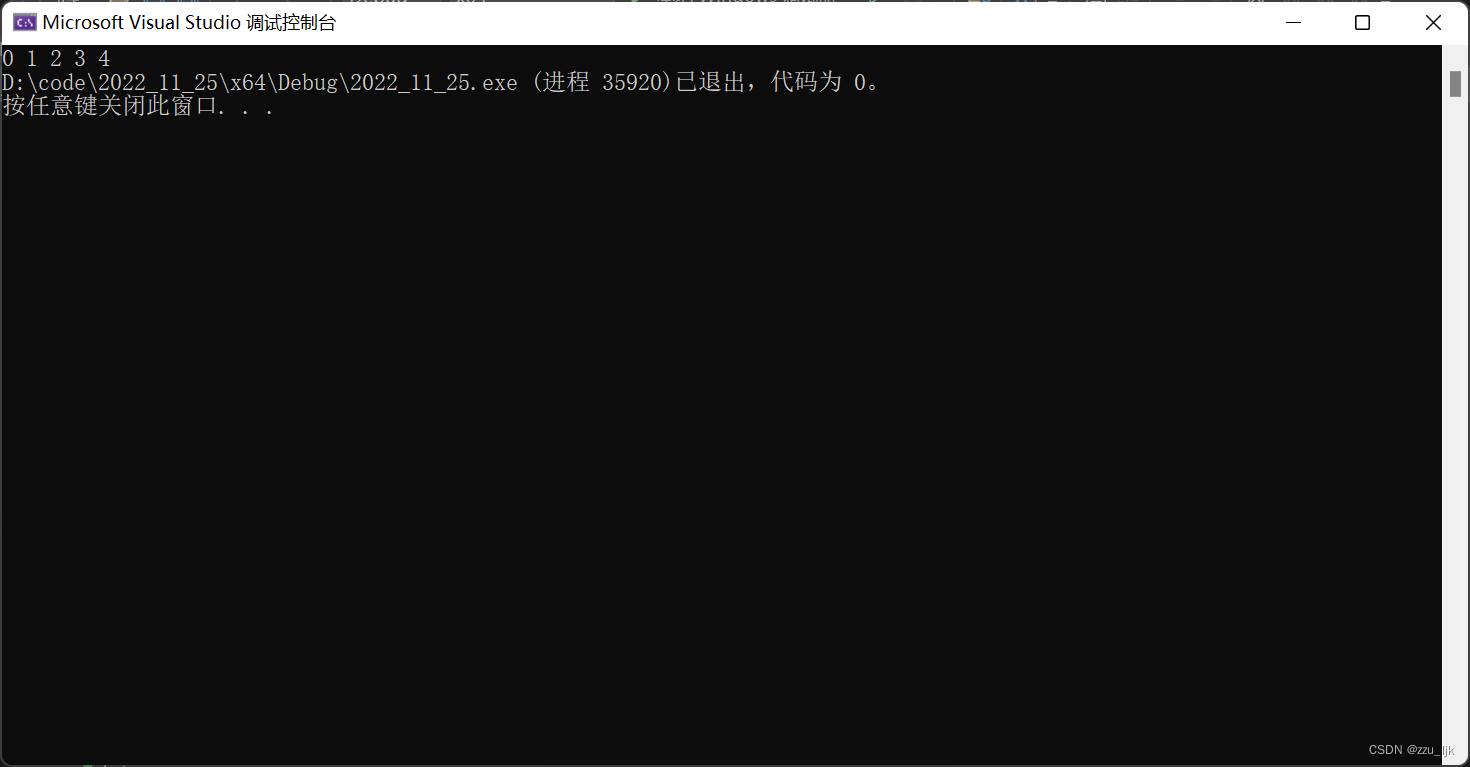
在这里插入图片描述
结果符合我们的预期，说明我们是正确的，可以用这个方法得到相同数据的所有下标。

在指定位置后插入

这个就需要借助查找函数来实现了，查找到某个位置，然后进行插入。
和头插一样，它需要从后往前挪动数据。

void SepListInsert(SL* ps, int pos, SLDataType x)
{
	assert(ps);

	CheckCapacity(ps);

	int i = 0;
	for (i = ps->size; i > pos + 1; i--)
		ps->a[i] = ps->a[i - 1];

	ps->a[pos + 1] = x;
	ps->size++;
}

有了这个函数，我们是不是可以对头插和尾插作一些优化呢？使得头插和尾插更简洁一些
是可以的！

头插时，我们设计的插入函数是插入下一个位置，如果要插入到下标为0的位置上，那么我们应该传入-1作为位置参数。

void SepListPushFront(SL* ps, SLDataType x)
{
	assert(ps);

	SepListInsert(ps, -1, x);
}

而尾插时，我们需要传入ps->size - 1作为参数

void SepListPushBack(SL* ps, SLDataType x)
{
	assert(ps);
	
	SepListInsert(ps, ps->size - 1, x);
}

是不是很方便呢？

删除指定位置的数据

和头删一样，需要从前往后挪动数据。

void SepListErase(SL* ps, int pos, SLDataType x)
{
	assert(ps);
	assert(ps->size > 0);

	int i = 0;
	for (i = pos; i < ps->size - 1; i++)
		ps->a[i] = ps->a[i + 1];

	ps->size--;
}

实现了这个函数以后，我们也能对头删和尾删作出进一步的优化。

void SepListPopFront(SL* ps)
{
	assert(ps);
	
	SepListErase(ps, 0);
}

void SepListPopBack(SL* ps)
{
	assert(ps);
	
	SepListErase(ps, ps->size - 1);
}

怎么样，是不是很方便呢？

顺序表的销毁

所有的功能实现好之后，我们实现最后一个接口函数，也就是销毁顺序表

void SepListDestroy(SL* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->size = ps->capacity = 0;
}

至此，顺序表的所有功能我们都已经实现完了，实践才是最重要的，快去试着实现一个顺序表吧！
下面附上所有接口函数的代码

void SepListInit(SL* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->size = ps->capacity = 0;
}


void SepListPushBack(SL* ps, SLDataType x)
{
	assert(ps);
	
	SepListInsert(ps, ps->size - 1, x);
}

void SepListPopBack(SL* ps)
{
	assert(ps);
	
	SepListErase(ps, ps->size - 1);
}

void SepListPushFront(SL* ps, SLDataType x)
{
	assert(ps);

	SepListInsert(ps, -1, x);
}

void SepListPopFront(SL* ps)
{
	assert(ps);
	
	SepListErase(ps, 0);
}

void SepListPrint(SL* ps)
{
	assert(ps);
	int i = 0;
	for (i = 0; i < ps->size; i++)
		printf("%d ", ps->a[i]);
}

int SepListFind(SL* ps, int pos, SLDataType x)
{
	assert(ps);
	int i = 0;
	for (i = pos; i < ps->size; i++)
		if (ps->a[i] == x)
			return i;

	return -1;
}

void CheckCapacity(SL* ps)
{
	if (ps->size == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		SLDataType* tmp = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newCapacity;
	}
}

void SepListInsert(SL* ps, int pos, SLDataType x)
{
	assert(ps);

	CheckCapacity(ps);

	int i = 0;
	for (i = ps->size; i > pos + 1; i--)
		ps->a[i] = ps->a[i - 1];

	ps->a[pos + 1] = x;
	ps->size++;
}

void SepListErase(SL* ps, int pos)
{
	assert(ps);
	assert(ps->size > 0);

	int i = 0;
	for (i = pos; i < ps->size - 1; i++)
		ps->a[i] = ps->a[i + 1];

	ps->size--;
}

1.3 顺序表的OJ题目

移除元素

题目链接：移除元素
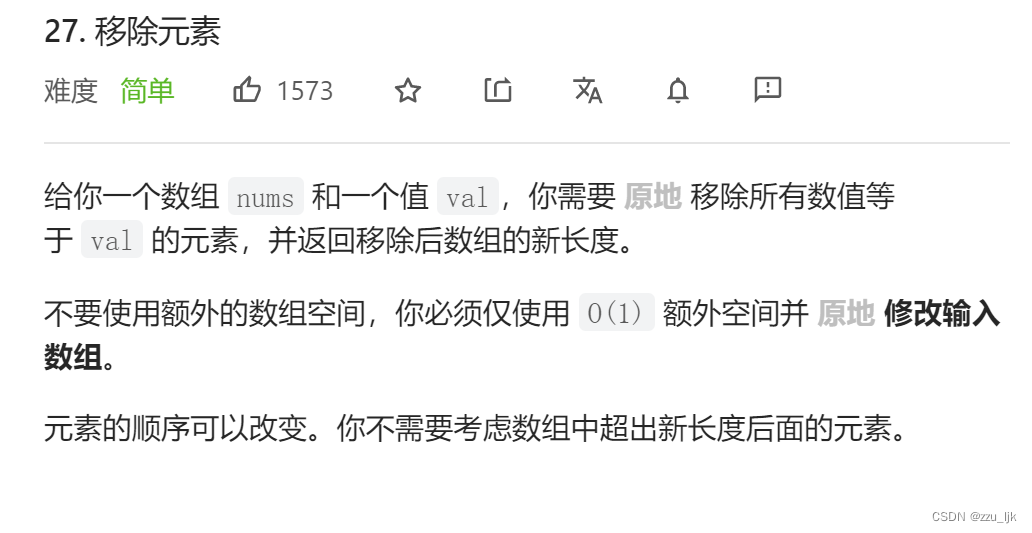
在这里插入图片描述
这道题目呢并不难，这里想通过这道题目提供一种解题的方法：双指针法！

首先我们定义int变量作为数组的下标，用下标模拟指针的实现。
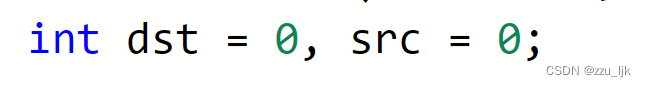
在这里插入图片描述
如果遇到等于val的值，src就往后走，一直向后探索，直到遇到一个不为val的值。
如果遇到不等于val的值，我们就把src指向的值赋值给dst，然后dst向后移一个位置，表示在下一个位置继续接受src的值，同时src也要向后走一步。
它的核心思想就是src探路，dst在src后面，如果src遇到的值不为val，那么就将这个值赋给dst，否则就继续向后走。
这里为了更好地理解，我们不妨画上几张图。
在这个图中我随便创建了一个数组，并且假设val为2.
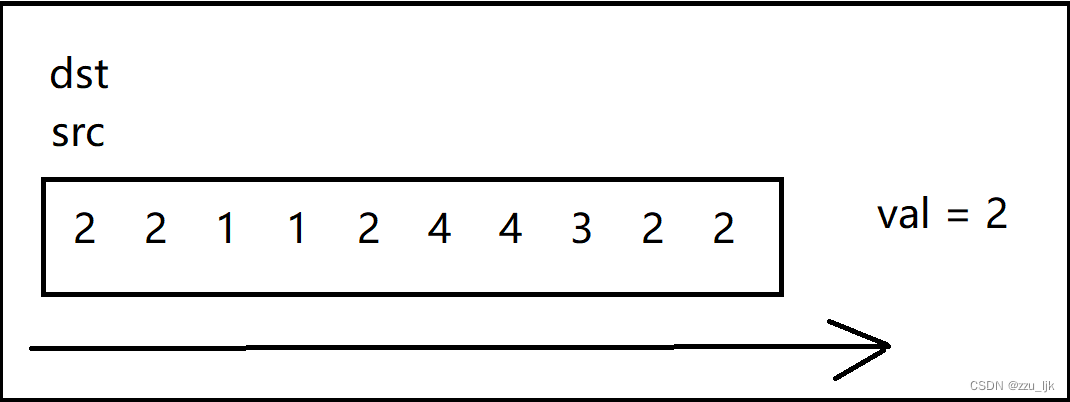
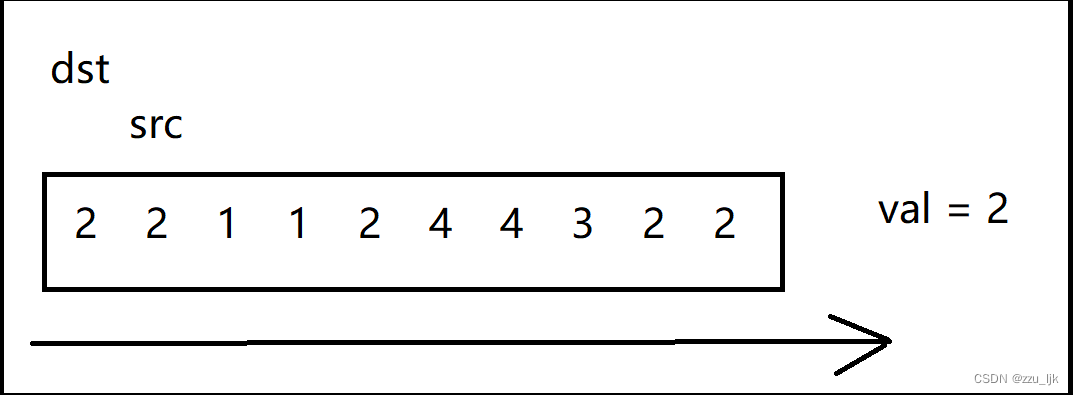
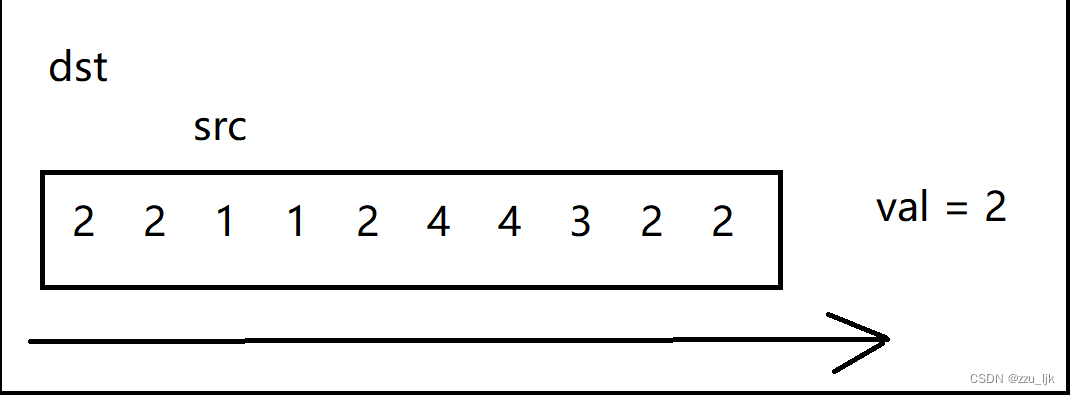
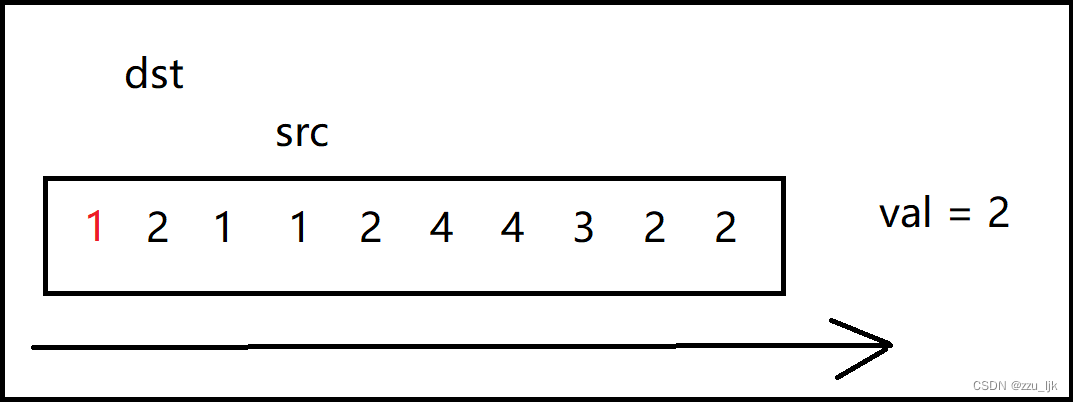
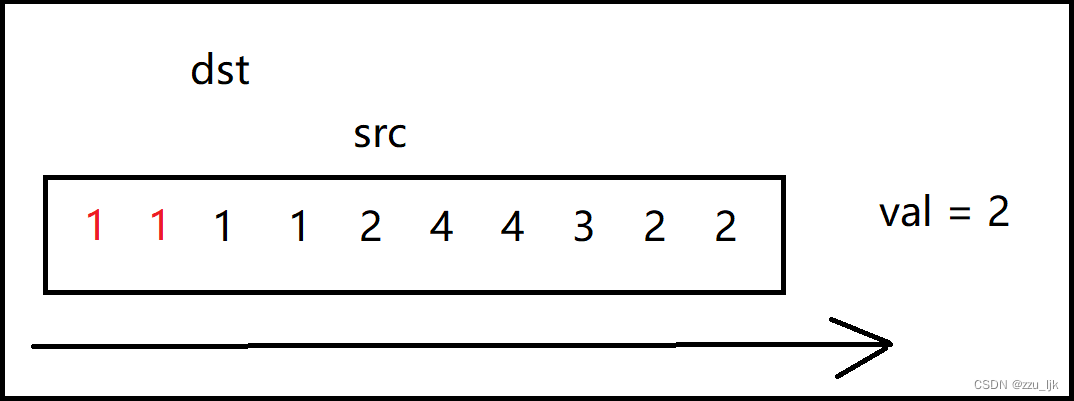
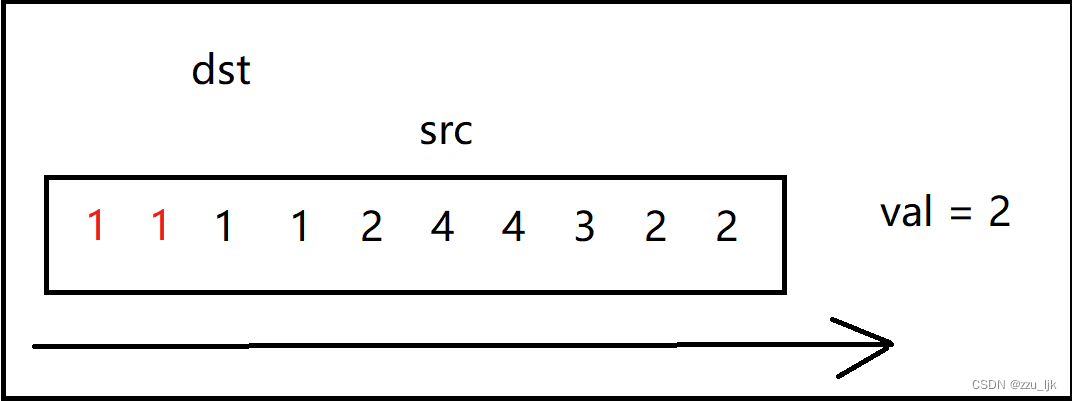
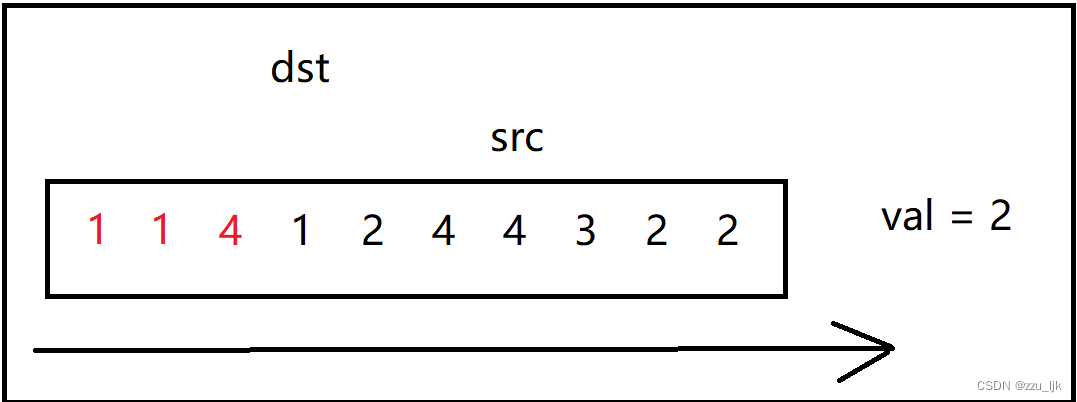
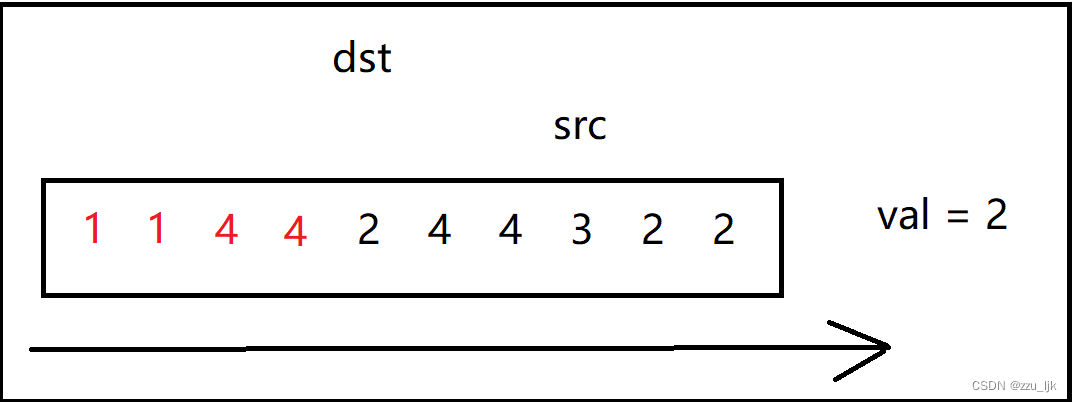
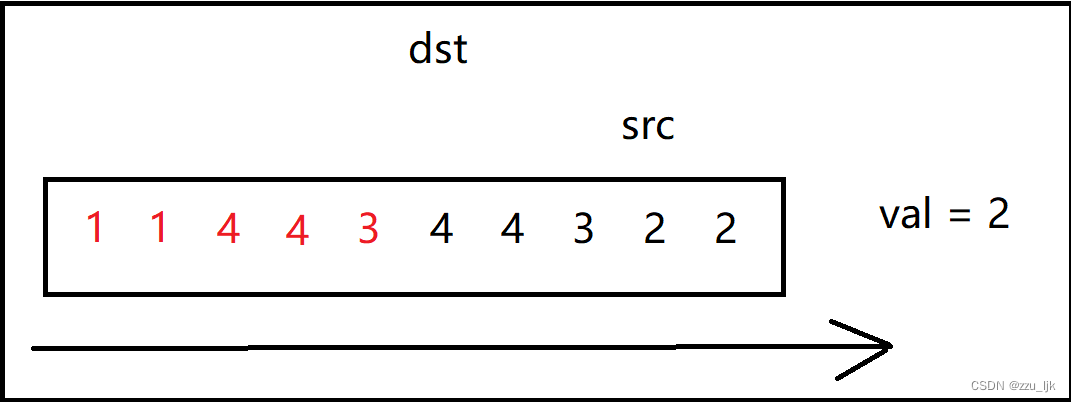
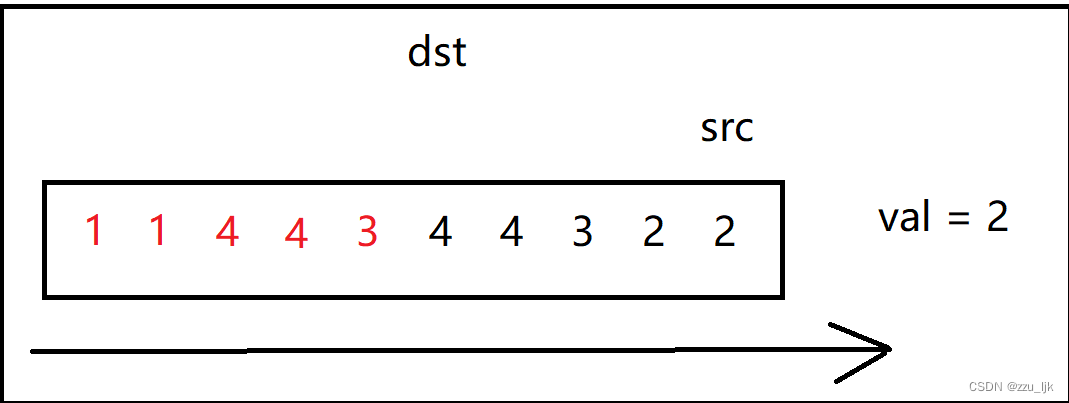
在这里插入图片描述

代码如下：

int removeElement(int* nums, int numsSize, int val){
    int dst = 0, src = 0;
    while(src < numsSize)
    {
        if (nums[src] == val)
        {
            src++;
        }
        else
        {
            nums[dst] = nums[src];
            dst++;
            src++;
        }
    }

    return dst;
}

在这里插入图片描述

删除有序数组中的重复项

题目链接：删除有序数组中的重复项
在这里插入图片描述

这道题的话就和上一道题很相似了，都是运用双指针法。
我们仍然运用两个变量src和dst，仍然是src在前面探路，dst在后面接收src的值。

int removeDuplicates(int* nums, int numsSize){
    int dst = 0, src = 1;
    while (src < numsSize)
    {
        if (nums[dst] == nums[src])
        {
            src++;
        }
        else
        {
            dst++;
            nums[dst] = nums[src];
            src++;
        }
    }

    return dst + 1;
}

但要注意的时，这道题的返回值与上一道题不同，让一道题在每次赋值之后都将dst加上1，这道题在赋值之前加1。所以这道题如果要返回数据总大小的话，应该反回的是dst + 1。
在这里插入图片描述

合并两个有序数组

题目链接：合并两个有序数组
在这里插入图片描述
题目要求合并两个有序数组到第一个数组中，并且要求合并后的顺序仍是非递减顺序。
那也就是说，我们要把两个数组的内容在第一个数组中排序。
如果你要先放小的，那么这道题目会非常的麻烦。考虑的情况实在是太多了，为了简化代码。我们可以选择先开始拍大的。
首先啊，如果数组nums2的长度为0，那么就不用排了，直接结束就行。
在这里插入图片描述
接着我们求出合并后数组的大小，记为len。
大小可不是最后一个元素的下标，大小-1后应该再作为下标。

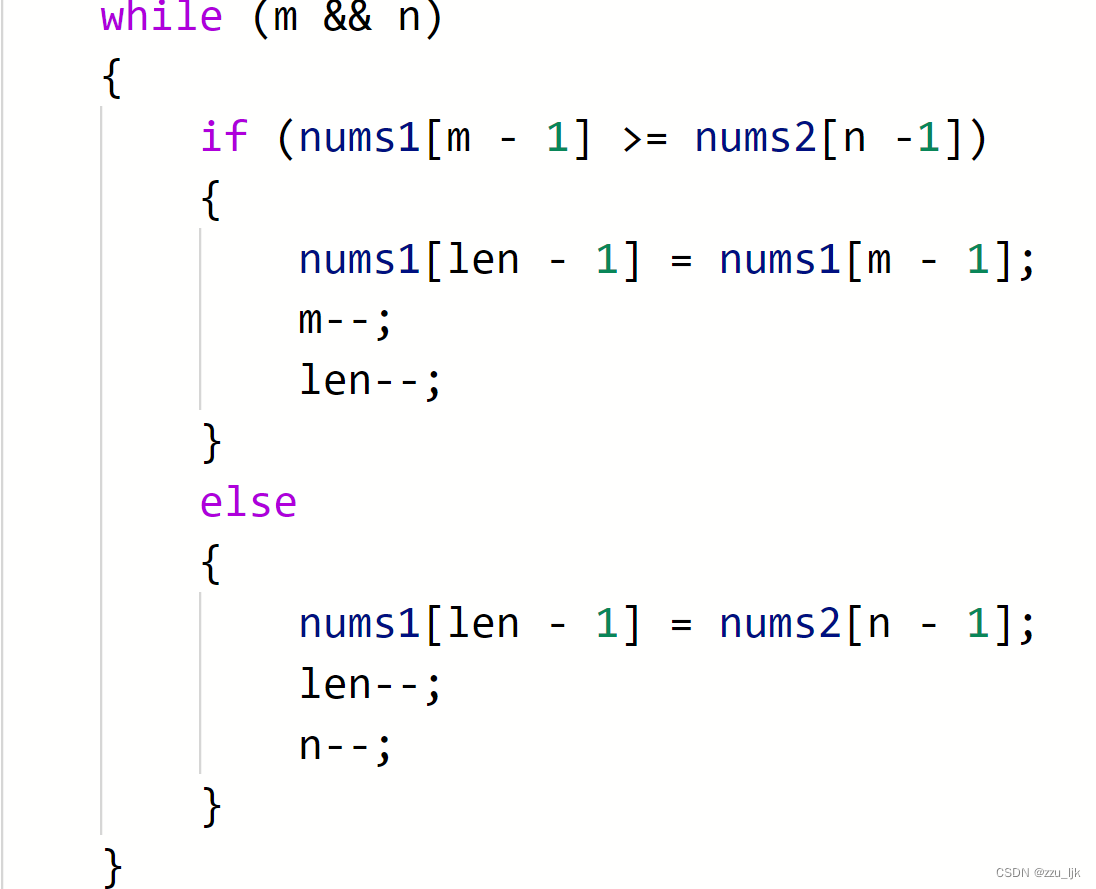
在这里插入图片描述
当m和n其中有一个为0时循环就结束了，然后继续用不为0的那个进行赋值。

整体代码如下：

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
    if (n == 0) return;
    int len = m + n;
    while (m && n)
    {
        if (nums1[m - 1] >= nums2[n -1])
        {
            nums1[len - 1] = nums1[m - 1];
            m--;
            len--;
        }
        else
        {
            nums1[len - 1] = nums2[n - 1];
            len--;
            n--;
        }
    }
    while (m)
    {
        nums1[len - 1] = nums1[m - 1];
        len--;
        m--;
    }
    while (n)
    {
        nums1[len - 1] = nums2[n - 1];
        len--;
        n--;
    }
}

在这里插入图片描述

顺序表到此结束，下面我们开始链表

2.链表

2.1 链表的大致介绍

顺序表的物理结构是连续的，但链表的物理结构就不定连续了。链表的每一个节点都是一个结构体，这个结构体即包含了这个节点的数据，又包含了一个指针，指针指向下一个节点。
所以说，链表在逻辑上是连续的，而逻辑上的连续是通过指针来实现的。
链表的逻辑结构如下
在这里插入图片描述
其实并没有什么箭头，箭头是我们想象出来的，我们要找到下一个节点靠的是指针。

2.2 单向不带头不循环链表的代码实现

单向不带头不循环链表可以说是最复杂的链表了，同时它也是最常考的。所以它虽然难，但是我们也必须要学会它。

typedef int SLTDataType;

typedef struct SList
{
	SLTDataType data;
	struct SList* next;
}SList;

这样做的好处也就不用我多说了吧？在顺序表那里已经详细介绍过了。
然后就是各种接口函数的声明

// 链表节点的创建
SLNode* BuySLNode(SLTDataType x);

// 链表的尾插
void SListPushBack(SLNode** pphead);

// 链表的尾删
void SListPopBack(SLNode** pphead);

// 链表的头插
void SListPushFront(SLNode** pphead);

// 链表的头删
void SListPopFront(SLNode** pphead);

// 链表的打印
void SListPrint(SLNode* phead);

// 在链表中查找指定元素
SLNode* SListFind(SLNode* phead, SLTDataType x);

// 在链表的指定位置之前进行插入
void SListInsert(SLNode** pphead, SLNode* pos, SLTDataType x);

// 在链表的指定位置之后进行插入
void SListInsertAfter(SLNode* pos, SLTDataType x);

// 删除链表的指定节点位置
void SListErase(SLNode** pphead, SLNode* pos);

// 删除链表指定节点之后的位置
void SListEraseAfter(SLNode* pos);

链表节点的创建

创建一个链表节点并返回，这个挺简单，应该不用多说

SLNode* BuySLNode(SLTDataType x)
{
	SLNode* newNode = (SLNode*)malloc(sizeof(SLNode));
	if (newNode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newNode->data = x;
	newNode->next = NULL;

	return newNode;
}

链表的尾插

我们首先创建一个链表节点的指针并初始化为空。
然后插入数据，改变该指针的指向。
注意：我们改变的是指针的指向，改变的是指针的值，而不是指针所指向的变量的值。
所以，当链表为空进行尾插时，我们应该传入链表指针的地址，而尾插函数的形参应该是一个二级指针。下面的很多涉及到链表的插入或者删除都要知道这一点！！！
在这里插入图片描述

然后进行尾插时，我们还要分情况讨论。
链表为空是一种情况，我们直接让新节点作为头即可。
链表不为空又是另一种情况，这种情况比较麻烦，我们还需要找到链表的尾并且进行连接。

void SListPushBack(SLTNode** pphead, SLTDataType x)
{
	SLTNode* newNode = BuySLNode(x);

	if (*pphead == NULL)
	{
		*pphead = newNode;
	}
	else
	{
		SLTNode* cur = *pphead;
		while (cur->next)
		{
			cur = cur->next;
		}
		cur->next = newNode;
	}
}

链表的尾删

和尾插一样，都要分情况讨论。
如果链表只剩下一个节点，直接删除即可。
如果链表还有很多节点，那么我们还需要找到最后一个节点。删除最后一个节点的同时还需将上一个节点的next置为空，那么再找最后一个节点的同时我们还需要找到最后一个节点的上一个节点。
最后可不要忘了释放最后一个节点，否则会造成内存泄漏。

void SListPopBack(SLTNode** pphead)
{
	assert(*pphead);

	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
	}
	else
	{
		SLTNode* cur = (*pphead)->next;
		SLTNode* prev = *pphead;
		while (cur->next)
		{
			prev = cur;
			cur = cur->next;
		}
		prev->next = NULL;
		free(cur);
	}
}

链表的头插

链表的头插就比较简单了，不需要进行特判。直接将新节点作为头链接进入链表即可。

void SListPushFront(SLTNode** pphead, SLTDataType x)
{
	SLTNode* newNode = BuySLNode(x);
	newNode->next = *pphead;
	*pphead = newNode;
}

链表的头删

头删和头插一样简单，直接操作即可。

void SListPopFront(SLTNode** pphead)
{
	assert(*pphead);

	SLTNode* tmp = *pphead;
	*pphead = (*pphead)->next;
	free(tmp);
}

链表的打印

链表的打印也是没什么，直接将链表遍历即可。

void SListPrint(SLTNode* phead)
{
	assert(phead);
	SLTNode* cur = phead;
	while (cur)
	{
		printf("%d->", cur->data);
		cur = cur->next;
	}
	printf("NULL\n");
}

在链表中查找指定元素

直接遍历链表，查找元素，如果找到，返回该节点的地址。如果未找到，返回空指针。

SLTNode* SListFind(SLTNode* phead, SLTDataType x)
{
	assert(phead);

	SLTNode* cur = phead;
	while (cur)
	{
		if (cur->data == x)
			return cur;

		cur = cur->next;
	}
	return NULL;
}

如果要查找多个元素也可以，只需再加一个形参，表示开始遍历的位置即可。

SLTNode* SListFind(SLTNode* phead, SLTNode* pos, SLTDataType x)
{
	assert(phead);
	assert(pos);

	SLTNode* cur = pos;
	while (cur)
	{
		if (cur->data == x)
			return cur;

		cur = cur->next;
	}
	return NULL;
}

在链表的指定位置之前进行数据的插入

在位置之前进行插入，那新插入的那个节点应该要和那个位置之前的节点相连接。但是只用cur的话又不找不到之前的节点，所以这里我们应该用两个变量，分别记录当前节点和当前节点的上一个节点的地址。
当然啦，这里还是要分情况讨论的。
如果该指定位置就是链表的头，直接插入即可。
如果不是，遍历链表，看是否能找到该指定位置。

void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)
{
	assert(*pphead);
	assert(pos);

	SLTNode* newNode = BuySLNode(x);

	if (*pphead == pos)
	{
		newNode->next = pos;
		*pphead = newNode;
	}
	else
	{
		SLTNode* cur = *pphead;
		SLTNode* prev = NULL;
		while (cur)
		{
			prev = cur;
			cur = cur->next;
			if (cur == pos)
			{
				newNode->next = cur;
				prev->next = newNode;
				return;
			}
		}
	}
}

在链表的指定位置之后进行数据的插入

这个的函数实现起来是比上一个函数更加简单的，因为它之后的节点通过next就可以找到了，所以只需要定义一个变量。
但是这个函数也有一定的局限性，因为只能在指定位置的之后插入，所以它是无法改变头结点的。
这里也有一个和上面函数不同的地方。因为刚才说到，它是无法改变头节点的，并且我们上面函数传二级指针是考虑到了修改头节点的情况，所以它不需要传二级指针，并且也不用传头指针，只需传入要插入的节点的地址即可。

void SListInsertAfter(SLTNode* pos, SLTDataType x)
{
	assert(pos);

	SLTNode* newNode = BuySLNode(x);
	
	newNode->next = pos->next;
	pos->next = newNode;
}

删除链表指定的节点

和在指定位置之前进行数据的插入一样，都要用两个变量并且进行分类讨论。

void SListErase(SLTNode** pphead, SLTNode* pos)
{
	assert(*pphead);
	assert(pos);

	if (*pphead == pos)
	{
		SLTNode* tmp = *pphead;
		*pphead = (*pphead)->next;
		free(tmp);
	}
	else
	{
		SLTNode* cur = *pphead;
		SLTNode* prev = NULL;
		while (cur)
		{
			prev = cur;
			cur = cur->next;
			if (cur == pos)
			{
				pos->next = cur->next;
				free(cur);
				return;
			}
		}
	}
}

删除链表指定位置节点之后的节点

设计这个函数就不用那么复杂了，但同样地，它不能修改链表的头，不需要用二级指针传入链表的头，并且需要断言它的next不能为空。

void SListEraseAfter(SLTNode* pos)
{
	assert(pos);
	assert(pos->next);

	SLTNode* next = pos->next->next;
	free(pos->next);
	pos->next = next;
}

至此，所有接口函数实现完成，下面附上接口函数的总代码
快尝试去实现一下把！

void SListPushBack(SLTNode** pphead, SLTDataType x)
{
	SLTNode* newNode = BuySLNode(x);

	if (*pphead == NULL)
	{
		*pphead = newNode;
	}
	else
	{
		SLTNode* cur = *pphead;
		while (cur->next)
		{
			cur = cur->next;
		}
		cur->next = newNode;
	}
}

SLTNode* BuySLNode(SLTDataType x)
{
	SLTNode* newNode = (SLTNode*)malloc(sizeof(SLTNode));
	if (newNode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newNode->data = x;
	newNode->next = NULL;

	return newNode;
}

void SListPrint(SLTNode* phead)
{
	SLTNode* cur = phead;
	while (cur)
	{
		printf("%d->", cur->data);
		cur = cur->next;
	}
	printf("NULL\n");
}

void SListPopBack(SLTNode** pphead)
{
	assert(*pphead);

	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
	}
	else
	{
		SLTNode* cur = (*pphead)->next;
		SLTNode* prev = *pphead;
		while (cur->next)
		{
			prev = cur;
			cur = cur->next;
		}
		prev->next = NULL;
		free(cur);
	}
}

void SListPushFront(SLTNode** pphead, SLTDataType x)
{
	SLTNode* newNode = BuySLNode(x);
	newNode->next = *pphead;
	*pphead = newNode;
}

void SListPopFront(SLTNode** pphead)
{
	assert(*pphead);

	SLTNode* tmp = *pphead;
	*pphead = (*pphead)->next;
	free(tmp);
}

SLTNode* SListFind(SLTNode* phead, SLTNode* pos, SLTDataType x)
{
	assert(phead);
	assert(pos);

	SLTNode* cur = pos;
	while (cur)
	{
		if (cur->data == x)
			return cur;

		cur = cur->next;
	}
	return NULL;
}

void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)
{
	assert(*pphead);
	assert(pos);

	SLTNode* newNode = BuySLNode(x);

	if (*pphead == pos)
	{
		newNode->next = pos;
		*pphead = newNode;
	}
	else
	{
		SLTNode* cur = *pphead;
		SLTNode* prev = NULL;
		while (cur)
		{
			prev = cur;
			cur = cur->next;
			if (cur == pos)
			{
				newNode->next = cur;
				prev->next = newNode;
				return;
			}
		}
	}
}

void SListInsertAfter(SLTNode* pos, SLTDataType x)
{
	assert(pos);

	SLTNode* newNode = BuySLNode(x);
	
	newNode->next = pos->next;
	pos->next = newNode;
}

void SListErase(SLTNode** pphead, SLTNode* pos)
{
	assert(*pphead);
	assert(pos);

	if (*pphead == pos)
	{
		SLTNode* tmp = *pphead;
		*pphead = (*pphead)->next;
		free(tmp);
	}
	else
	{
		SLTNode* cur = *pphead;
		SLTNode* prev = NULL;
		while (cur)
		{
			prev = cur;
			cur = cur->next;
			if (cur == pos)
			{
				prev->next = cur->next;
				free(cur);
				return;
			}
		}
	}
}

void SListEraseAfter(SLTNode* pos)
{
	assert(pos);
	assert(pos->next);

	SLTNode* next = pos->next->next;
	free(pos->next);
	pos->next = next;
}

2.3 双向带头循环链表的实现（最强大的链表）

链表可以分为单向还是双向，带头还是不带头，循环还是不循环，这三种条件组合一下就有八种情况。
上面介绍的单向不带头不循环链表是最复杂的链表，但是也是最常考的链表。
下面我要介绍的双向带头循环链表是八中链表中最强大的链表，不接受任何反驳！！！
其他链表在它那里就是个那什么。

在这里插入图片描述

链表节点的创建

在每次插入节点我们都要创建一个新节点，如果每次都书写这个创建新节点的代码显得很麻烦，所以我们不妨就用一个函数来将这个链接节点的创建的代码封装起来。

void BuyListNode(LDataType x)
{
	LN* newNode = (LN*)malloc(sizeof(LN));
	if (newNode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newNode->data = x;
	newNode->next = NULL;
	newNode->prev = NULL;

	return newNode;
}

链表的初始化

首先实现链表的初始化，由于我们这是一个带头的链表，所以在初始化之前我们应该先创建一个指向头节点的指针。并且因为我们要改变这个头节点的内容，所以我们应该在初始化时传入这个头节点的地址。
又因为呢它是一个循环的链表，所以在创建时我们要将头节点的next和prev指向它自己。

void ListInit(LN** ppHead)
{
	assert(*ppHead);
	*ppHead = BuyListNode(-1);
	(*ppHead)->next = (*ppHead);
	(*ppHead)->prev = (*ppHead);
}

链表的尾插

双向链表的尾插就比较简单了，不需要像单链表那样分情况讨论，也不用利用循环来找尾。因为头节点的prev就是尾。

void ListPushBack(LN* pHead, LDataType x)
{
	assert(pHead);

	LN* newNode = (LN*)malloc(sizeof(LN));

	LN* tail = pHead->prev;
	tail->next = newNode;
	newNode->prev = tail;
	newNode->next = pHead;
}

链表的尾删

使用链表的尾删之前需要需要断言这个链表不为空，也就是断言头节点的下一个节点不是它自己，最后不要忘了释放。

void ListPopBack(LN* pHead)
{
	assert(pHead);
	assert(pHead->next != pHead);

	LN* tail = pHead->prev;
	LN* prev = tail->prev;

	prev->next = pHead;
	pHead->prev = prev;

	free(tail);
}

链表的头插

没有什么难度啊，创建新节点直接插入即可。
注意的就是每次插入要将节点的next和prev都改变。

void ListInsert(LN* pos, LDataType x)
{
	assert(pos);

	LN* newNode = BuyListNode(x);
	LN* prev = pos->prev;

	newNode->next = pos;
	pos->prev = newNode;
	prev->next = newNode;
	newNode->prev = prev;
}

链表的头删

同样没什么难度。通过这几个函数相信你能感受到双向带头循环链表的强大了。

void ListPopFront(LN* pHead)
{
	assert(pHead);
	assert(pHead->next != pHead);

	LN* del = pHead->next;

	pHead->next = del->next;
	del->next->prev = pHead;
	free(del);
}

找到链表的指定节点

直接遍历整个链表即可

LN* ListFind(LN* pHead, LDataType x)
{
	assert(pHead);
	assert(pHead->next != pHead);

	LN* cur = pHead->next;
	while (cur != pHead)
	{
		if (cur->data == x)
			return cur;
		cur = cur->next;
	}
	return NULL;
}

在链表的指定位置之前进行插入

不用进行循环找到指定位置和指定位置之前的位置了，是否简单多了呢？

void ListInsert(LN* pos, LDataType x)
{
	assert(pos);

	LN* newNode = BuyListNode(x);
	LN* prev = pos->prev;

	newNode->next = pos;
	pos->prev = newNode;
	prev->next = newNode;
	newNode->prev = prev;
}

同时，到了这里，我们就可以借助这个函数对头插和尾插进行改造了。
尾插

void ListPushBack(LN* pHead, LDataType x)
{
	assert(pHead);

	ListInsert(pHead->prev, x);
}

头插

void ListPushFront(LN* pHead, LDataType x)
{
	assert(pHead);

	ListInsert(pHead->next, x);
}

删除链表的指定位置

和上一次接口函数一样，都非常简单而粗暴

void ListErase(LN* pos)
{
	assert(pos);
	assert(pos->next != pos);

	LN* prev = pos->prev;
	LN* next = pos->next;

	prev->next = next;
	next->prev = prev;

	free(pos);
}

有了这个接口函数，我们也可以对头删和尾删进行改造了
尾删

void ListPopBack(LN* pHead)
{
	assert(pHead);
	assert(pHead->next != pHead);

	ListErase(pHead->prev);
}

头删

void ListPopFront(LN* pHead)
{
	assert(pHead);
	assert(pHead->next != pHead);

	ListErase(pHead->next);
}

链表的销毁

注意，链表的销毁需要传入二级指针，因为这里需要改变pHead的值并且释放pHead。

void ListDestroy(LN** pHead)
{
	assert(*pHead);

	LN* cur = *pHead;
	while (cur != pHead)
	{
		LN* next = cur->next;
		free(cur);
		cur = next;
	}
	free(*pHead);
	*pHead = NULL;
}

好了，双向链表的讲解也到此结束，赶快去尝试一下吧！
下面附上双向链表的接口函数的代码

void ListInit(LN** ppHead)
{
	*ppHead = BuyListNode(-1);
	(*ppHead)->next = (*ppHead);
	(*ppHead)->prev = (*ppHead);
}

LN* BuyListNode(LDataType x)
{
	LN* newNode = (LN*)malloc(sizeof(LN));
	if (newNode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newNode->data = x;
	newNode->next = NULL;
	newNode->prev = NULL;

	return newNode;
}

void ListPushBack(LN* pHead, LDataType x)
{
	assert(pHead);

	ListInsert(pHead->prev, x);
}	

void ListPrint(LN* pHead)
{
	assert(pHead);

	LN* cur = pHead->next;
	while (cur != pHead)
	{
		printf("%d ", cur->data);
		cur = cur->next;
	}
}

void ListPopBack(LN* pHead)
{
	assert(pHead);
	assert(pHead->next != pHead);

	ListErase(pHead->prev);
}

void ListPushFront(LN* pHead, LDataType x)
{
	assert(pHead);

	ListInsert(pHead->next, x);
}

void ListPopFront(LN* pHead)
{
	assert(pHead);
	assert(pHead->next != pHead);

	ListErase(pHead->next);
}

LN* ListFind(LN* pHead, LDataType x)
{
	assert(pHead);
	assert(pHead->next != pHead);

	LN* cur = pHead->next;
	while (cur != pHead)
	{
		if (cur->data == x)
			return cur;
		cur = cur->next;
	}
	return NULL;
}

void ListInsert(LN* pos, LDataType x)
{
	assert(pos);

	LN* newNode = BuyListNode(x);
	LN* prev = pos->prev;

	newNode->next = pos;
	pos->prev = newNode;
	prev->next = newNode;
	newNode->prev = prev;
}

void ListErase(LN* pos)
{
	assert(pos);
	assert(pos->next != pos);

	LN* prev = pos->prev;
	LN* next = pos->next;

	prev->next = next;
	next->prev = prev;

	free(pos);
}

void ListDestroy(LN** pHead)
{
	assert(*pHead);

	LN* cur = *pHead;
	while (cur != pHead)
	{
		LN* next = cur->next;
		free(cur);
		cur = next;
	}
	free(*pHead);
	*pHead = NULL;
}

2.4 链表的OJ题目

移除链表元素

题目链接：移除链表元素
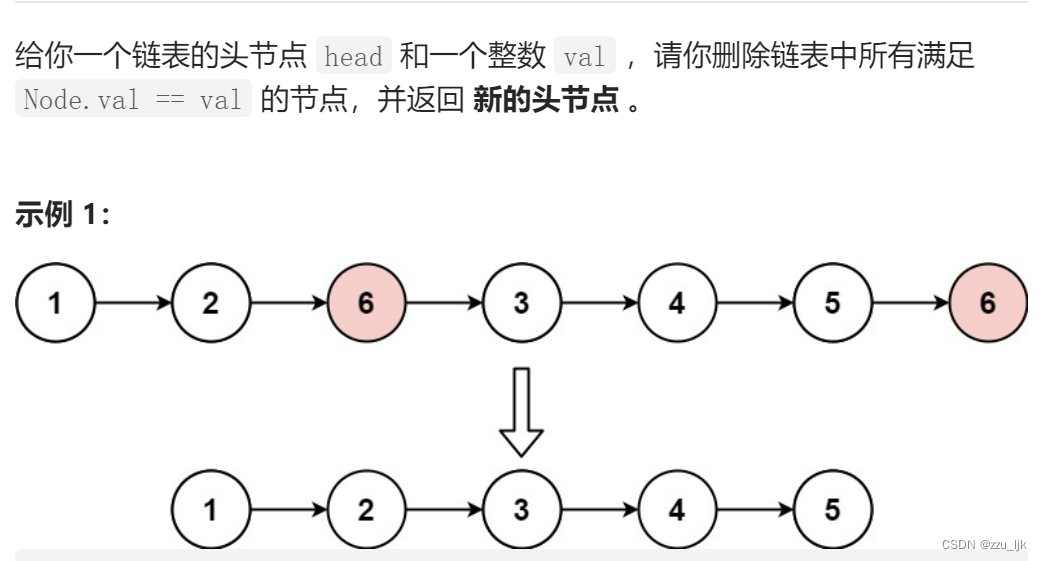
在这里插入图片描述

这道题呢总体上不难，但是有许多细节需要注意，一不留心就会出错。其实做链表题的最好方法就是画图，可能画图需要十五分钟，但是写代码只需要五分钟。但是如果你不画图，那么你写代码需要十分钟，debug又需要三十分钟。
下面开始这道题的讲解
写这种题可以先看看题目中的测试用例，可能题目的测试用例中会给出一些特例。
在这里插入图片描述
注意到这个测试用例，如果链表为空，那么就直接返回空即可。

再看这个更特殊的测试用例，整个链表的元素都是我们要删除的元素。

这个时候我们既要删除指定元素，又要改变链表的头。也就是说，删除链表元素的同时我们要将head向后移动。为了方便head的删除和移动，这里定义一个新的变量next
在这里插入图片描述
注意：这里while循环的条件中必须要把head放在前面，当head为空时那样就不会访问head的val了，防止出现非法解引用的情况

在这个while循环结束后我们又要判断head是否为空（不要只局限于这个测试用例，可能有链表的头为要删除的节点但链表不全为要删除的节点的情况）
同时既然这个测试用例要判断链表是否为空，上一个测试用例也要判断链表是否为空的情况。那我们不妨将它们合并一下。
合并后的代码如下：
在这里插入图片描述
在上面这两个特例处理完后，因为测试用例1适用的情况太少，所以我专门创建了一个测试用例来进行画图解释

在这里插入图片描述
当进行上面代码的移动之后，情况如下。

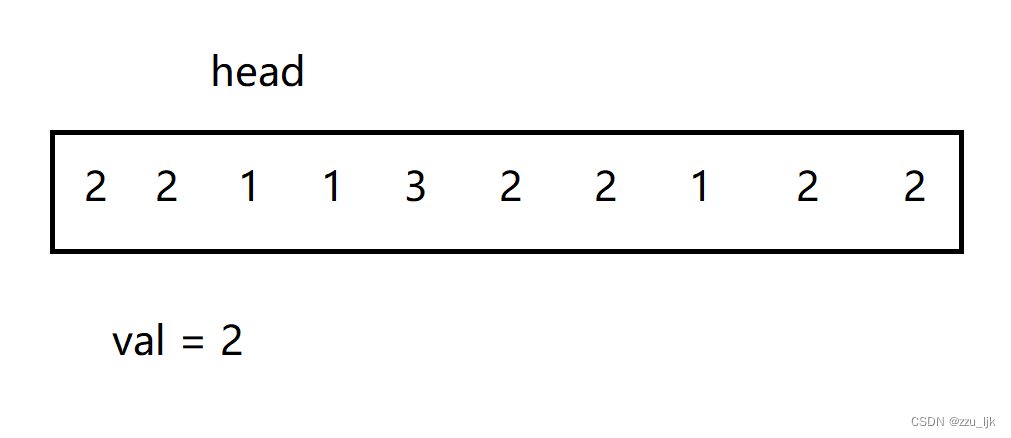
然后我们新定义指针变量prev和cur，cur用于遍历链表，而prev用于记录cur的上一个节点。

然后我们进入while循环，循环的条件是cur不为空，在循环中我们分情况讨论。
如图所示，当节点内存储的值就不为val时，cur和prev继续向后走。当节点呢存储的值就为val时，我们便删除这个节点，但是我们删除之后又找不到下一个节点，所以应该先用next记录下个节点，再删除当前节点。同时将next的值赋给cur，并且将cur再赋给prev的next，也就是说将新节点与原来值不为val的节点连接起来。
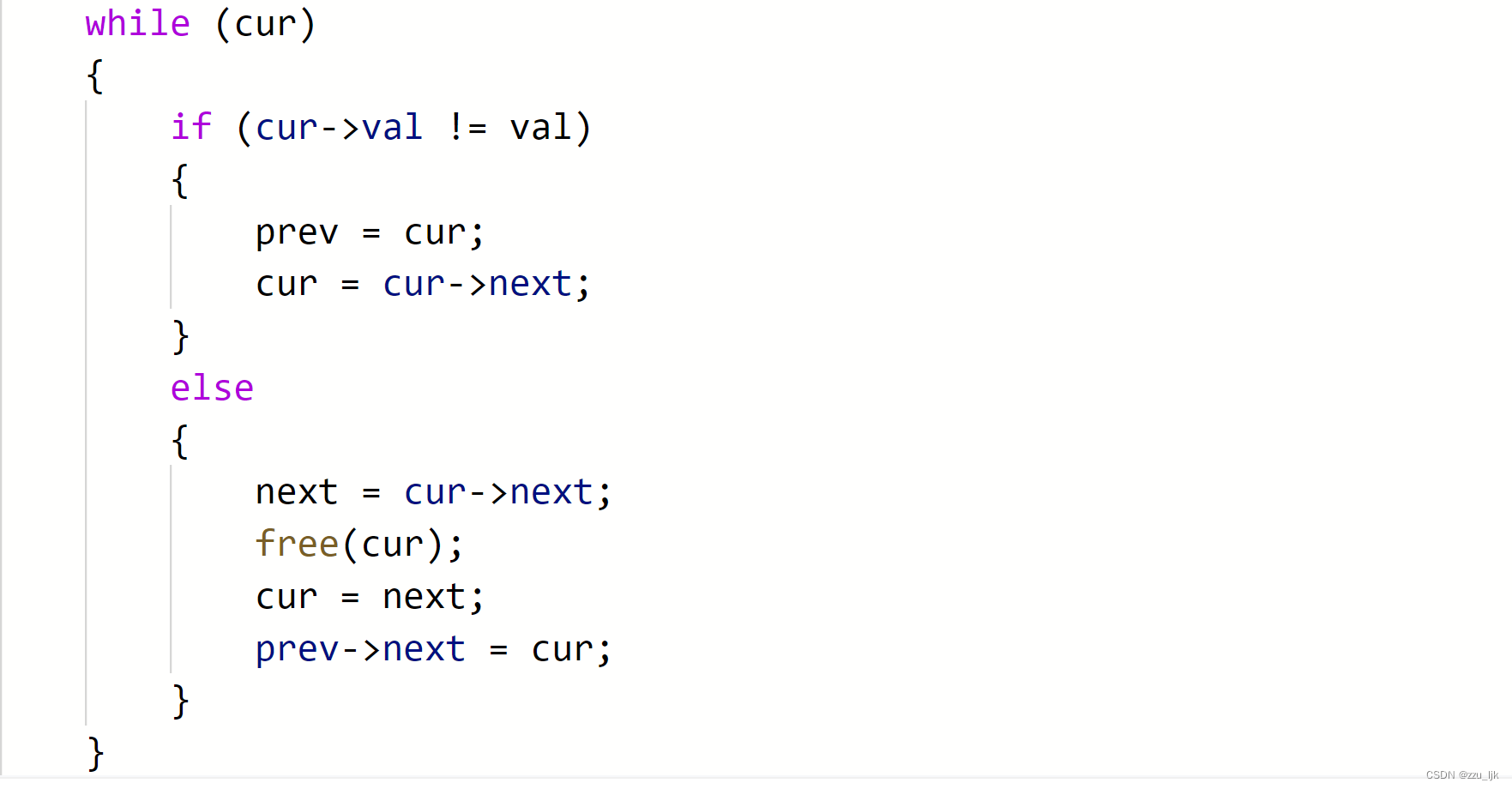
在这里插入图片描述
最后返回head即可
整体代码如下：

struct ListNode* removeElements(struct ListNode* head, int val){
    struct ListNode* next = NULL;
    while (head && head->val == val)
    {
        next = head->next;
        free(head);
        head = next;
    }
    if (head == NULL)
        return NULL;
    
    struct ListNode* cur = head->next;
    struct ListNode* prev = head;
    while (cur)
    {
        if (cur->val != val)
        {
            prev = cur;
            cur = cur->next;
        }
        else 
        {
            next = cur->next;
            free(cur);
            cur = next;
            prev->next = cur;
        }
    }

    return head;
}

反转链表

题目链接：反转链表
利用了三个指针直接对原链表进行反转。用cur记录当前节点，用prev记录当前节点的上一个节点，用next记录当前节点的下一个节点。
这种方法有很多细节需要注意，下面我开始讲解。
首先如果题目所给链表为空或者链表只有一个节点，那么这时候是不需要进行反转的，直接返回即可。
这里要注意的是这两个条件不能前后颠倒，因为head可能是空的，你如果先判断head的next可能会导致访问空指针的问题。
在这里插入图片描述
然后定义三个指针。

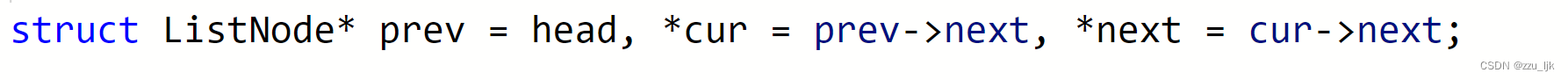
这三个指针的位置如图所示。

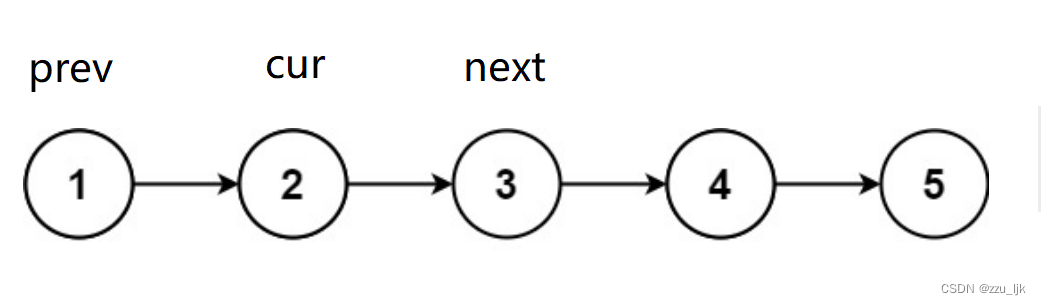
切记，在进行反转之前，你必须把头节点的next置为空。

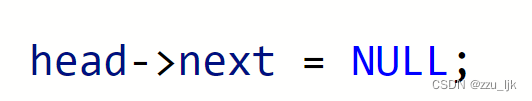
如图所示

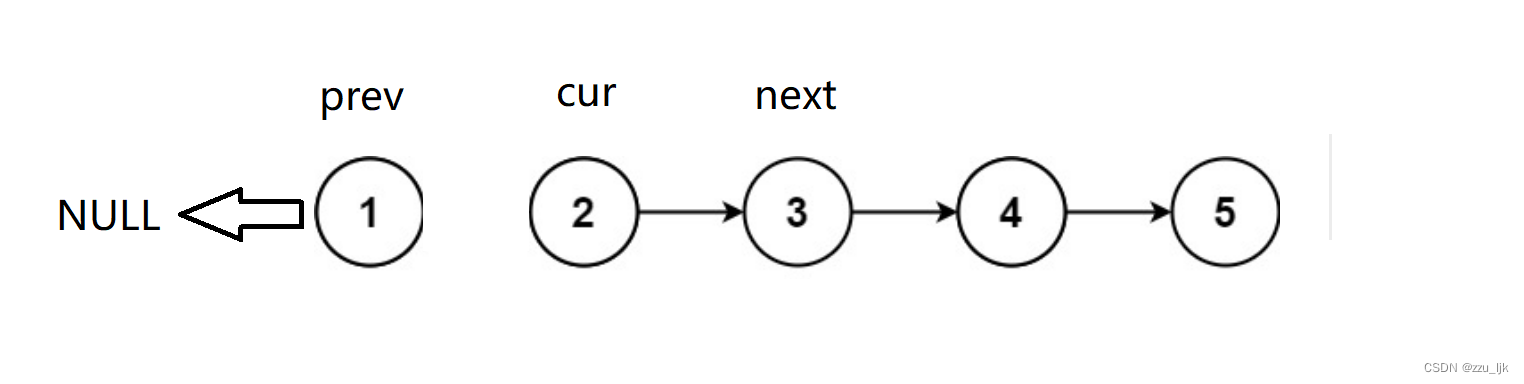
然后，你需要将cur的next置为prev。

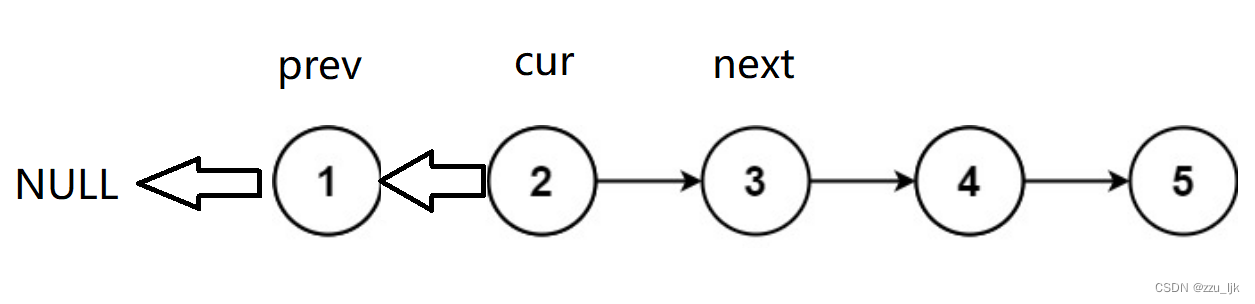
向后迭代，将cur的值赋给prev，将next值赋给cur，将next的next的值赋给next。

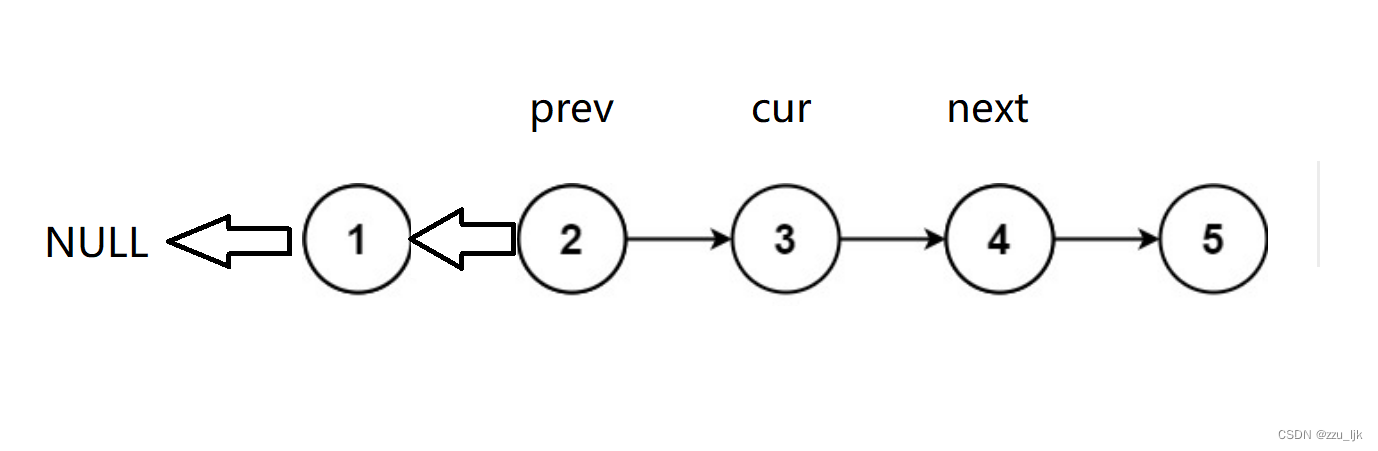
在这里插入图片描述
循环结束的条件是什么？我们一直向后迭代，看看最后是怎样的。
是不是当cur为空循环就结束呀。并且我们需注意，在next向后移动时我们得判断next是否为空，否则可能出现访问空指针的错误。

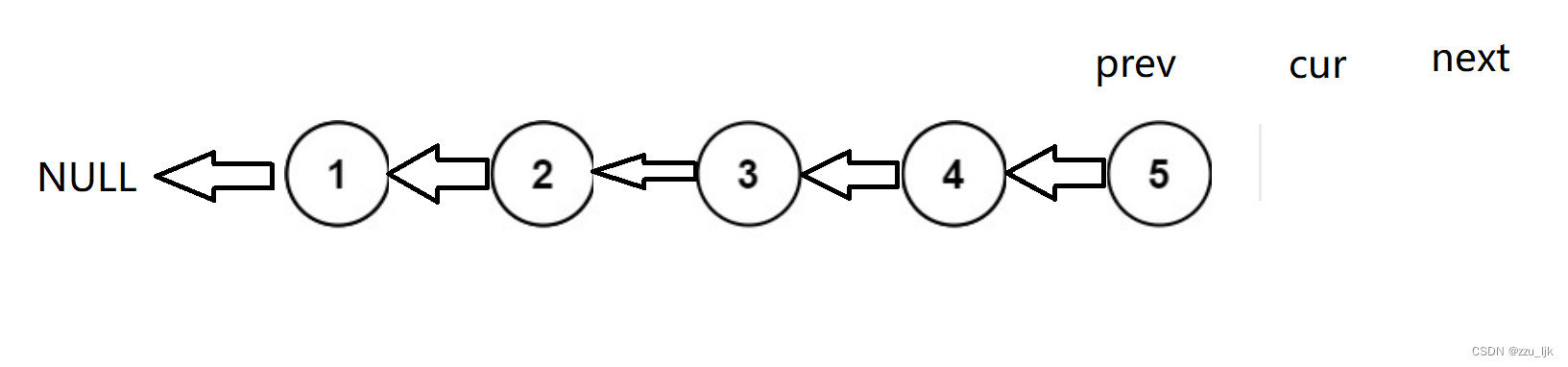
最后返回prev即可。
整体代码如下：

struct ListNode* reverseList(struct ListNode* head){
    if (head == NULL || head->next == NULL)
        return head;
    
    struct ListNode* prev = head, *cur = prev->next, *next = cur->next;
    
    head->next = NULL;

    while (cur)
    {
        cur->next = prev;
        prev = cur;
        cur = next;
        if (next)
            next = next->next;
    }

    return prev;
}