戳气球实验报告
目录
一、题目
二、分析原问题并做调整
三、分析子问题及其递推关系
四、确定dp数组的计算顺序
五、复杂度分析
六、具体实现代码
七、填表示例寻找最优解和最优方案
八、总结
九、致谢
一、题目
有n个气球,编号为0到n-1,每个气球都有一个分数,存在nums数组中。每次戳气球i可以得到的分数为 nums[left] * nums[i] * nums[right],left和right分别表示i气球相邻的两个气球。当i气球被戳爆后,其左右两气球即为相邻。要求戳爆所有气球,得到最多的分数。
备注:
1.你可以假设nums[-1] = nums[n] = 1。-1和n位置上的气球不真实存在,因此不能戳爆它们。
2.0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
二、分析原问题并做调整
运用动态规划算法的一个重要条件:子问题必须独立。对于此问题,必须巧妙地定义 dp 数组的含义,避免子问题产生相关性,才能推出合理的状态转移方程。要想定义 dp 数组,这里需要对问题进行一个简单地转化。题目说可以认为 nums[-1] = nums[n] = 1,那么我们先直接把这两个边界加进去,形成一个新的数组 points:
int maxCoins(vector<int>& nums) {
int n = nums.size();
Vector<int> points(n+2);// 两端加入两个虚拟气球
points[0] = points[n + 1] = 1;//题目给的条件0和n+1气球吹破为1
for (int i = 1; i <= n; i++) {
points[i] = nums[i - 1];改变问题后points[i]就应该等于原问题的nums[i-1],此处i从1开始到n结束,因为我们对points已经考虑过了0和n+1的 情况了,而nums是从0~n-1
}
// ...
}
现在气球的索引变成了从 1 到 n,points[0] 和 points[n+1] 可以认为是两个「虚拟气球」。因此我们可以改变问题:在一排气球 points 中,请你戳破气球 0 和气球 n+1 之间的所有气球(不包括 0 和 n+1),使得最终只剩下气球 0 和气球 n+1 两个气球,最多能够得到多少分?
三、分析子问题及递推关系
我们用dp[i][j] = x 表示,戳破气球 i 和气球 j 之间(开区间,不包括 i 和 j)的所有气球,可以获得的最高分数为 x。根据这个定义,题目要求的结果就是 dp[0][n+1] 的值,而 base case 就是 dp[i][j] = 0,其中 0 <= i <= n+1, j <= i+1,因为这种情况下,开区间 (i, j) 中间根本没有气球可以戳。
// base case 已经都被初始化为 0
vector<vector > dp(n + 2, vector(n + 2));
//构造动态二维dp[][]数组,转化后的问题是有n+2个气球(2个虚拟)
现在我们要根据这个 dp 数组来推导状态转移方程了,实际上就是在思考怎么「做选择」,也就是这道题目最有技巧的部分:想求戳破气球 i 和气球 j 之间的最高分数,如果「正向思考」,就不是动态规划了。我们需要「反向思考」,想一想气球 i 和气球 j 之间最后一个被戳破的气球可能是哪一个?其实气球 i 和气球 j 之间的所有气球都可能是最后被戳破的那一个,不防假设为 k。回顾动态规划的步骤,这里其实已经找到了状态和选择:i 和 j 就是两个状态,最后戳破的那个气球 k 就是选择。
根据刚才对 dp 数组的定义,如果最后一个戳破气球 k,dp[i][j] 的值应该为:
dp[i][j] = dp[i][k] + dp[k][j]
+ points[i]*points[k]*points[j]
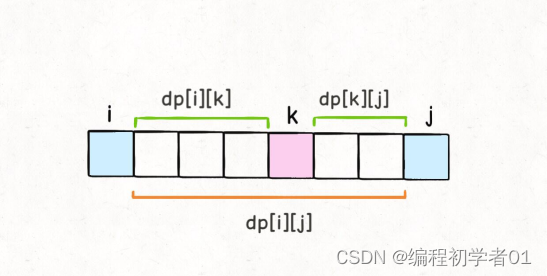
结合这个图,就能体会出 dp 数组定义的巧妙了。由于是开区间,dp[i][k] 和 dp[k][j] 不会影响气球 k;而戳破气球 k 时,旁边相邻的就是气球 i 和气球 j 了,最后还会剩下气球 i 和气球 j,这也恰好满足了 dp 数组开区间的定义。要想最后戳破k气球,那么开区间(i,k)和(k,j)内的气球也得先戳破。最后只剩i,j,k三个气球,则分数为 points[i]*points[k]*points[j]。戳破开区间 (i, k) 和开区间 (k, j) 的气球最多能得到的分数就是 dp[i][k] 和 dp[k][j],这恰好就是我们对 dp 数组的定义。
那么,对于一组给定的 i 和 j,我们只要穷举 i < k < j 的所有气球 k,选择得分最高的作为 dp[i][j] 的值即可,这也就是状态转移方程:
// 最后戳破的气球是哪个?
for (int k = i + 1; k < j; k++) { //穷举戳破i到j之间的气球 ,i<k<j,故k从i+1到j-1
int sum = points[i] * points[k] * points[j];
sum += dp[i][k] + dp[k][j];
dp[i][j] = max(dp[i][j], sum);
}
递归方程为:
dp[i][j]=
max{ dp[i][k] + dp[k][j]+points[i]*points[k]*points[j] },i<j-1
0,i>=j-1
四、确定dp数组的计算顺序
除了获得了状态转移方程外,对于 k 的穷举仅仅是在做选择,但是应该如何穷举状态i 和 j ?
for (int i = ...; ; )
for (int j = ...; ; )
for (int k = i + 1; k < j; k++) { //穷举戳破i到j之间的气球 ,i<k<j,故k从i+1到j-1
int sum = points[i] * points[k] * points[j];
sum += dp[i][k] + dp[k][j];
dp[i][j] = max(dp[i][j], sum);
}
return dp[0][n+1];
关于「状态」的穷举,最重要的一点就是:状态转移所依赖的状态必须被提前计算出来。这道题举例,dp[i][j] 所依赖的状态是 dp[i][k] 和 dp[k][j],那么我们必须保证:在计算 dp[i][j] 时,dp[i][k] 和 dp[k][j] 已经被计算出来了(其中 i < k < j)。那么应该如何安排 i 和 j 的遍历顺序,来提供上述的保证呢?有一个技巧:根据 base case 和最终状态进行推导。
备注:最终状态就是指题目要求的结果,对于这道题目也就是 dp[0][n+1]。
我们先把 base case 和最终的状态在 DP table 上画出来:
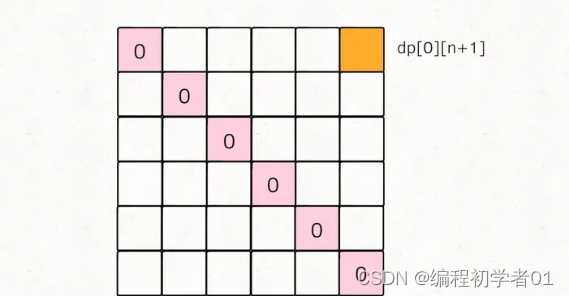
对于任一 dp[i][j],我们希望所有 dp[i][k] 和 dp[k][j] 已经被计算,画在图上就是这种情况:
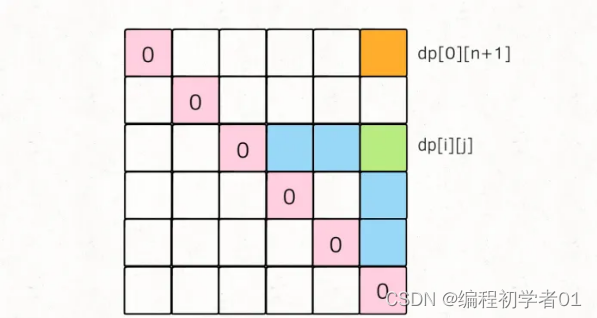
为了达到这个要求,我们小组打算自底向上,从左到右依次遍历:
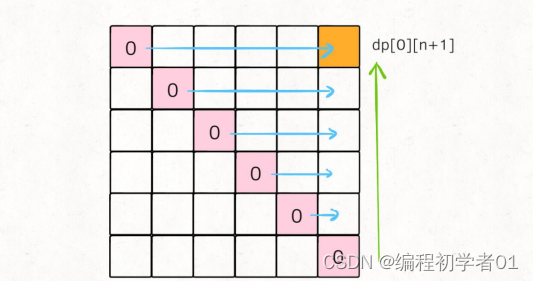
那么经过递归方程分析,我们要满足i,j之间有气球才可以戳破,那么至少j>=i+2才能满足中间有气球。则要有气球可戳,则i最大也就是n+1-2=n-1。j可能是i+1
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 2; j <= n + 1; j++) {
for (int k = i + 1; k < j; k++) { //穷举i到j之间的气球 ,i<k<j,故k从i+1到j-1
int sum = points[i] * points[k] * points[j];
sum += dp[i][k] + dp[k][j];
dp[i][j] = max(dp[i][j], sum);
}
}
}
return dp[0][n + 1];//返回最大值,戳破0~n+1之间的气球
五、复杂度分析
时间复杂度:O(n3),其中 O(n) 是气球数量。状态数为 n2,状态转移复杂度为 O(n),最终复杂度为 O(n2×n)=O(n3);
空间复杂度:O(n2),其中 n 是气球数量。
六、具体实现代码
#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
#define N 100
int maxCoins(vector<int>& nums) { //参数是用vector做的动态数组nums,也是初始问题
int n = nums.size(); //数组长度,其实也就是气球个数n(0~n-1一共是n个)
vector<vector<int> > dp(n + 2, vector<int>(n + 2)); //构造动态二维dp[][]数组
vector<vector<int> > s(n + 2, vector<int>(n + 2));
vector<int> points(n + 2); //添加虚拟气球后改变问题的一维points[]数组 ,虚拟的2个气球是辅助功能,我们只需要戳两端中间的气球,即是开区间
points[0] = points[n + 1] = 1; //题目给的条件0和n+1气球吹破为1
for (int i = 1; i <= n; i++) {
points[i] = nums[i - 1]; //改变问题后points[i]就应该等于原问题的nums[i-1],此处i从1开始到n结束,因为我们对points已经考虑过了0和n+1的 情况了,而nums是从0~n-1
}
for (int i = n - 1; i >= 0; i--) { //i从下往上,i从倒数第二个开始,遍历到0。
for (int j = i + 2; j <= n + 1; j++) {//j从左往右,遍历到n+1 ,分析关系的j=i+2
s[i][j] = i;
for (int k = i + 1; k < j; k++) { //穷举i到j之间的气球 ,i<k<j,故k从i+1到j-1
int sum = points[i] * points[k] * points[j];
sum += dp[i][k] + dp[k][j];
//dp[i][j] = max(dp[i][j], sum);
if (sum > dp[i][j]) {
dp[i][j] = sum;
s[i][j] = k;
}
}
}
}
cout << "k表:" << endl;
for (int i = 0; i <= n + 1; i++) {
for (int j = 0; j <= n + 1; j++) {
cout.width(7);
cout << s[i][j];
}
cout << endl;
}
cout << "分数表为:" << endl;
for (int i = 0; i <= n + 1; i++) {
for (int j = 0; j <= n + 1; j++) {
cout.width(7);
cout << dp[i][j];
}
cout << endl;
}
return dp[0][n + 1];//返回最大值,戳破0~n+1之间的气球
}
int main() {
int n;
cout << "请输入气球个数:" << endl;
cin >> n;
cout << "请输入各气球分数:" << endl;
vector<int> nums(n);
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
cout << "获得的最大分数为:" << maxCoins(nums);
return 0;
}
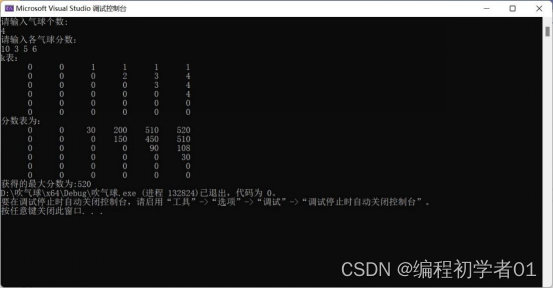
七、填表示例寻找最优解和最优方案
通过递归方程dp[i][j]=
max{ dp[i][k] + dp[k][j]+points[i]*points[k]*points[j] },i<j-1
0,i>=j-1
我们可以把dp[][]表填好
dp[][]表如下:
i\j 0 1 2 3 4 5
0 0 0 30 200 510 520(优)
1 0 0 150 450 510
2 0 0 90 108
3 0 0 30
4 0 0
5 0
K(rec) 0 1 2 3 4 5
0 0 0 1 1 1 1
1 0 0 2 3 4
2 0 0 3 4
3 0 0 4
4 0 0
5 0
自底向上,从左到右填表过程:
dp[3][5]=dp[3][4]+dp[4][5]+P3P4P5=0+0+5*6=30(k=4),
dp[2][4]=dp[2][3]+dp[3][4]+P2P3P4=0+0+356=90(k=3),
dp[2][5]=max{
dp[2][3]+dp[3][5]+P2P3P5=0+30+35=45,
dp[2][4]+dp[4][5]+P2P4P5=90+0+36=108
}=108(k=4),
dp[1][3]=dp[1][2]+dp[2][3]+P1P2P3=0+0+1035=150(k=2),
dp[1][4]=max{
dp[1][2]+dp[2][4]+P1P2P4=0+90+1036=270,
dp[1][3]+dp[3][4]+P1P3P4=150+0+1056=450
}=450(k=3),
dp[1][5]=max{
dp[1][2]+dp[2][5]+P1P2P5=0+108+103=138,
dp[1][3]+dp[3][5]+P1P3P5=150+30+105=230,
dp[1][4]+dp[4][5]+P1P4P5=450+0+10*6=510
}=510(k=4),
dp[0][2]=dp[0][1]+dp[1][2]+P0P1P2=0+0+103=30(k=1),
dp[0][3]=max{
dp[0][1]+dp[1][3]+P0P1P3=0+150+105=200,
dp[0][2]+dp[2][3]+P0P2P3=30+0+35=45
}=200(k=1),
dp[0][4]=max{
dp[0][1]+dp[1][4]+P0P1P4=0+450+106=510,
dp[0][2]+dp[2][4]+P0P2P4=30+90+36=138,
dp[0][3]+dp[3][4]+P0P3P4=200+0+56=230
}=510(k=1)
dp[0][5]=max{
dp[0][1]+dp[1][5]+P0P1P5=0+510+10=520,
dp[0][2]+dp[2][5]+P0P2P5=30+108+3=141,
dp[0][3]+dp[3][5]+P0P3P5=200+30+5=235,
dp[0][4]+dp[4][5]+P0P4P5=510+0+6=516
}=520(k=1)
追溯过程:
dp[0][5】(k=1)→dp[1][5】(k=4)→dp[1][4】(k=3)→dp[1][3】(k=2)
那么戳爆气球的顺序为2→3→4→1
我们所要求得最优解为dp[0][5],其值为520.但是我们还要通过rec表来追溯其最优方案,也就是戳气球的顺序。
dp[0][5]的rec=1,则最终戳破的气球是1。则dp[0][5]=dp[0][1]+dp[1][5].那么我们可以追踪到dp[1][5],其rec=4,则戳破的气球为4。则dp[1][5]=dp[1][4]+dp[4][5].那么就可以追踪到dp[1][4],其rec=3,则戳破的气球为3。则dp[1][4]=dp[1][3]+dp[3][4],那么我们可以追踪到dp[1][3],其rec=2,则戳破的气球为2。最后dp[1][3]=dp[1][2]+dp[2][3],不可再追踪。由于我们是每次考虑最后被戳破的气球,因此所得顺序应该完全颠倒,对于此问题,戳破气球的顺序为2—3—4—1,也就是我们最优方案。
八、总结
这道题其实并不难,关键在于 dp 数组的定义,需要避免子问题互相影响,所以我们反向思考,将 dp[i][j] 的定义设为开区间,考虑最后戳破的气球是哪一个,以此构建了状态转移方程。对于如何穷举「状态」,我们使用了小技巧,通过 base case 和最终状态推导出 i,j 的遍历方向,保证正确的状态转移。总而言之,收获颇丰。
九、致谢
感谢老师,感谢学校,感谢国家!