我们在之前的学习里面已经发现了,搜索二叉树是有一些问题的。它可能会存在单边树的问题,如果你插入的值是有序的话,就会导致这个问题。 那我们肯定是要来解决一下的,如何解决呢?
》一种解决方案是AVL树,还有另一种解决方案是红黑树。我们先把AVL树讲了:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。它尽可能的去保证平衡,但是平衡呢,不是说相等,而是高度差不超过1。并且它不仅仅是针对整棵树,而是针对每一颗子树。
》一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
·它的左右子树都是AVL树
·左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
》也就是任何一颗子树的高度差都不超过1。大家看,他这个地方确定的一个点是什么呢?高度差不超过1,不是相等,按道理,平衡平衡不应该是相等吗?但是无法做到相等,因为插入节点的个数是无法确定的,只能退而求其次,左右高度差不超过1。
》我们不实现Key 的结构了,直接实现KV结构。我们定义一个AVLTreeNode结构体,将树的节点结构体定义出来,它里面有pair<K, V> _kv,还有左右指针,AVLTreeNode*_left,AVLTreeNode* _right,因为我们后面要进行回溯,所以,还得有一个父指针,AVLTreeeNode* _parent;除此之外,还得有一个平衡因子 int _bf,它使用来干嘛的呢?它_bf = 右子树 - 左子树的高度差。
》我们再继续往下面看,大家来看看增加的平衡因子成员变量,整体是一个什么样子呢?比如说,我的一棵树建好了,我根据我的平衡因子,每一颗子树的右子树高度-左子树高度 = _bf,若bf= -1那么左子树高1,bf = 1右子树高1。但是平衡因子并不是必须的,即AVL树并没有规定必须要设计平衡因子,这只是一个实现的选择,方便控制平衡。
template<class K, class V>
struct AVLTreeNode
{
pair<K, V> _kv;
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
// 右子树-左子树的高度差
int _bf; // balance factor
// AVL树并没有规定必须要设计平衡因子
// 只是一个实现的选择,方便控制平衡
};
》我们再来定义class AVLTree类,其中我们对AVLTreeNode节点进行typedef,typedef AVLTreeNode<K, V> Node;然后自然就要定义一个根节点成员变量Node* _root = nullptr;到目前为止,这棵树AVLTree啥都没有,只有一个根。
template class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
private:
Node* _root;
}
》我们现在是不是先来完成插入工作呀了,bool insert(const pair<K, V>& kv);其实大思路是分两步,1.按照搜索树的规则插入。搜索树规则默认是,大的插在右边,小的插在左边;2.看是否违反平衡规则,如果违反就要处理:旋转。所以,从大逻辑来说,AVL树有没有什么很难的呢?其实并没有,只是在搜索树的规则上引入了平衡规则。
》先不管其他的,先把insert()写好吧。首先判断根_root是否为空,为空的话,就new一个Node节点出来。然后如果不为空的时候怎么走?是不是比根大就向右走,比根小就向左走呀。在这里可以用递归,也可以用循环,我们就用循环吧。用循环的话,我们得有父节点。我们进行比较的话,得那就得定义一个Node* cur来和插入的值进行比较,并根据cur来判断结束条件。while(cur),当然是一直走到空的位置才进行插入我们的新值,否则就是一路比较下来,newnode大的话向右走,小的话向左走,也就是更新cur,但是都要先将我们的cur赋值给我们parent,然后再更新cur自己。当走到空了,cur = new Node(kv);那就再判断是插入左边还是插入右边,插入完之后,也不要忘了更新父节点。至此,我们insert()插入的基本逻辑已经完成了。
bool Insert(const pair<K, V>& kv)
{
// 1、搜索树的规则插入
// 2、看是否违反平衡规则,如果违反就需要处理:旋转
if (_root == nullptr)
{
_root = new Node(kv);
_root->_bf = 0;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
}
》然后将我们的AVLTreeNode的构造函数补充一下:
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _bf(0)
{}
一个节点的平衡因子默认一开始是0,一个节点的平衡因子受谁的影响呢?是不是受其孩子的影响呀。大家想想,我们插入一个节点之后,是会影响谁的平衡因子呢?是不是会影响我们父亲、爷爷以及更靠上层的跟节点呀,所以要想清楚,它会影响好多节点的平衡因子。
》我们插入了一个节点之后,我么你就考虑平衡的问题了。如果是你,你会如何进行平衡呢?平衡因子的绝对值不超过1,是不是就不需要平衡,如果超过了,我们才会去解决,平衡因子又是由我们的左右子树的高度差来决定的。我们新插入的值会影响它的祖先的平衡因子,其他的节点是不会受到影响的。
》既然我们插入了一个节点,我们下面就要继续做几步了。1.更新新插入节点的祖先的平衡因子。因为只有是我的祖先才会受我的影响。2.没有违反规则就结束了,违反规则,不平衡就要旋转处理。那我们如何更新祖先呢的平衡因子呢?
》是不是我们可以用我们的三叉链来回溯呀!所以,为什么要设计三叉链呀,是有原因的。我们继续分析,更新平衡因子,难道祖先的平衡因子一定是 +1吗?

当在此情况在9节点的右边插入一个新节点的时候,9节点的bf是不是+1,bf = 1,8这个节点是不是也要+1,bf = 2;还要不要继续向上更新?不需要了,因为已经违反规则了,需要处理完才能判断是否需要继续向上更新。新增节点的平衡因子必然是0,这不用说,但是在如下情况呢?

9节点的bf是要-1的,bf = -1,但是8节点的bf继续是+1,bf = 2;所以,通过这个可以看到,如果插入在右边,父亲的平衡因子会+1,但是插入在左边,父亲平衡因子会-1,但是8节点的平衡因子依然是+1,因为我新插入的节点相当于插入在8节点的右边,那么是不是相当于8的右树变高了,所以要+1;
》所以沿着祖先路径更新,如果if(cur == parent->right) 那么父节点的平衡因子_bf++,否则就是插入在左边吧,那平衡因子就是_bf–;
》还有一种情况,新节点插入在8节点的左边:

那么8节点的平衡因子就要-1,bf = 0,还需要向上更新吗?是不是说一定要更新到根呢?前面的情况,我们是能够理解,因为已经不平衡了,所以肯定要处理。但是在这里,对于7的平衡因子并不会有什么影响呀,那怎么办?怎么分析呢?一定是一次就不用更新了吗?不一定只更新一次呀,极端情况下是会更新很久的,比如给你一个这种情况:

因为新节点是插入9节点左边,所以bf-1,bf=-1,然后因为9节点是在8节点的右边,所以,bf+1,bf=1,还需要更新的,因为8节点是7节点的右边,所以7节点的bf+1,bf=1;因为7节点是5节点的右边所以bf+1,bf=1,直到更新到根了,在往上没得要跟新了,所以,不一定只更新一次。
》大家想一想,什么情况要继续往上更新呢?是不是子树的高度变了,就要往上更新了呀!子树的高度变了,就要继续往上更新,子树的高度不变则更新完成,子树违反平衡规则,则停止更新,旋转子树!

》首先,我们新增一个节点,它的父节点9是一定要更新平衡因子的,因为对我父节点来说,我新增了一个节点,我的子树必然发生变化,所以第一次是一定更新的。
》如果父亲节点9更新之后的平衡因子是1代表的是什么?即parent->_bf = 1,那么parent所在的子树的高度变不变呢?会变的!那么就要继续更新,说明原来是0,现在右边变高了,bf+1了,所以bf =1了,你在这里更新平衡因子无非就是++和–,我现在变成1,只有一种情况,就是我右边子树的高度变了,所以,我的平衡因子变为1,但是我原来的平衡因子是0 ,现在变1,说明右树变高了,所以高度变了,那么就要继续向上更新,如何更新呢?就是将cur->parent赋值给cur,即cur = cur->parent;紧接着parent也要变为parent的parent,即parent = parent->parent;cur9节点现在是parent8节点的右边,相当于原来右边的高度增加了1,parent的bf是右子树-左子树,那么bf是要+1,现在变成了2,如果变成了2说明什么呢?那么就要停止向上更新了,要进行处理了,这里的处理就会我们待会儿要讲的旋转。
》我们再来看一个:

我新增在你9节点的左边,你的bf肯定要变呀且要-1,那么此时9节点的平衡因子变为-1说明什么呢?那么parent9节点所在子树的高度变没变?变了,我原先是0,现在-1,变为bf = -1了,也就说明我的左边变高了,那么整体的高度会不会受影响呢?是会的!因为原来9节点的两边子树左右相等,现在左边变高了,那么继续向上更新, 8节点的bf变为2了。
》再来一个:

此时我在8节点的左边插入一个节点,此时8节点的平衡因子变为0,要不要向上更新呢?不用!因为高度不变,为什么呢?说明原来是1,现在变成0,之前一边高一边低,现在插入节点,只有一种情况,就是填上了矮的那一边,那么我的子树高度不变,会不会对上层有影响呢?是不会的!因为我8节点还没插入的时候,子树的高度就是1,右高左低,现在插入了,左边高了1,但是子树的高度并没有变,对上层没有影响,所以只需要更新一下8节点这么一个平衡因子。
》所以,要不要更新,取决于你的子树高度变不变。

搜索树要控制平衡,引入了平衡因子,那么我们就需要关注有没有平衡因子异常,如果异常就出问题了,没有异常就不用关心了。第二个,你插入一个节点要关注谁?你只会影响你的祖先的平衡因子,为什么呢?因为一个节点的平衡因子是由谁影响的呢?就是自己的子树!那么,我插入一个节点就会往上影响,所以,我们要做好最坏的打算一路更新到根,那么我们下面来更新一下平衡因子:
》更新到根的特征是什么呢?那就是父节点为nullptr空,即while(parent)。我新增的一个节点是在你右边,那父亲节点的平衡因子bf+1,即cur == parent->right,那么parent->_bf++,否则是不是就是parent->_bf–;接下来就是,是否需要继续向上更新的问题了,那就要看父亲的平衡因子了,如果父亲的子树高度变了就要更新,不变的话更新就完成了,如果高度违反了,就要停止更新,然后进行旋转处理。
》那么我们怎么分辨这几种情况来判断是否需要继续向上更新呢?父亲的平衡因子只可能有这么几种情况,0、1、-1、2、-2,不可能有其他情况,因为平衡因子是++或者–,插入之前就是AVL树就只有0、-1、1这三种情况,所以不可能超过2。
》所以,如果parent->bf = =0,那么就不用更新了,直接break;为什么停止更新呢?因为我们分析过了,因为如果是0了之后的话,我bf只可能是++或–了一下,那就说明插入节点。把你子树低的那一边填上去了。
》如果插入之后变成了parent->_bf = =1 || parent->_bf = =-1,说明什么呢?那是不是就是说明插入节点导致一边变高了,也就是子树的高度拜年了,要继续更新祖先。就要重新赋值cur和parent,即cur = cur->parent;parent = parent->parent;
》还有另外一种情况,就是平衡因子变成了2或者-2,即parent->_bf = =2 || parenrt->_bf = =-2,说明什么呢?你一定是由1或者-1变过来的。这是不是导致高的一边又变高了,导致子树不平衡----需要旋转处理。
》没有其他情况了,出现了就是插入之前的AVL就存在不平衡。
while (parent) // 最远要更新根
{
if (cur == parent->_right)
{
parent->_bf++;
}
else
{
parent->_bf--;
}
// 是否继续更新?
if (parent->_bf == 0) // 1 or -1 -》 0 插入节点填上矮的那边
{
// 高度不变,更新结束
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
// 0 -》 1 或 -1 插入节点导致一边变高了
{
// 子树的高度变了,继续更新祖先
cur = cur->_parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
// -1 or 1 -》 2 或 -2 插入节点导致本来高一边又变高了
{
// 子树不平衡 -- 需要旋转处理
// ...
}
else
{
// 插入之前AVL就存在不平衡子树,|平衡因子| >= 2的节点
assert(false);
}
}
现在只剩下一种情况,就是需要旋转,我们没有处理,我们先拿一种简单情况来说。

插入红色节点之后,父节点的bf会变成1,那么继续往上更新,继续会变成1,再继续往上走,bf变成2,此时就需要进行旋转处理。反正总之这是属于,右边高—左旋转。旋转的原则,1.保持搜索的规则;2.子树变平衡。
》我们来看看下面的分析:我们下图是代表所有情况的抽象图,长方形条表示的是子树,a、b、c子树有无数种情况,所以,我们就抽象表示,当然可以画几个具体的情况来看看。


当h=0的时候,然后就要进行更新bf了,这也是属于最简单的情况。

当h=1的时候,也会出现不平衡需要旋转了。
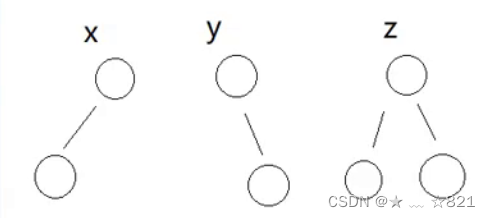
当h=2的时候就复杂了,因为高为2的子树有挺多种情况的。那么a、b、c子树就是那几种情况之一,那是是不是a、b、c就要任意组合。比如我们随便组合一个。
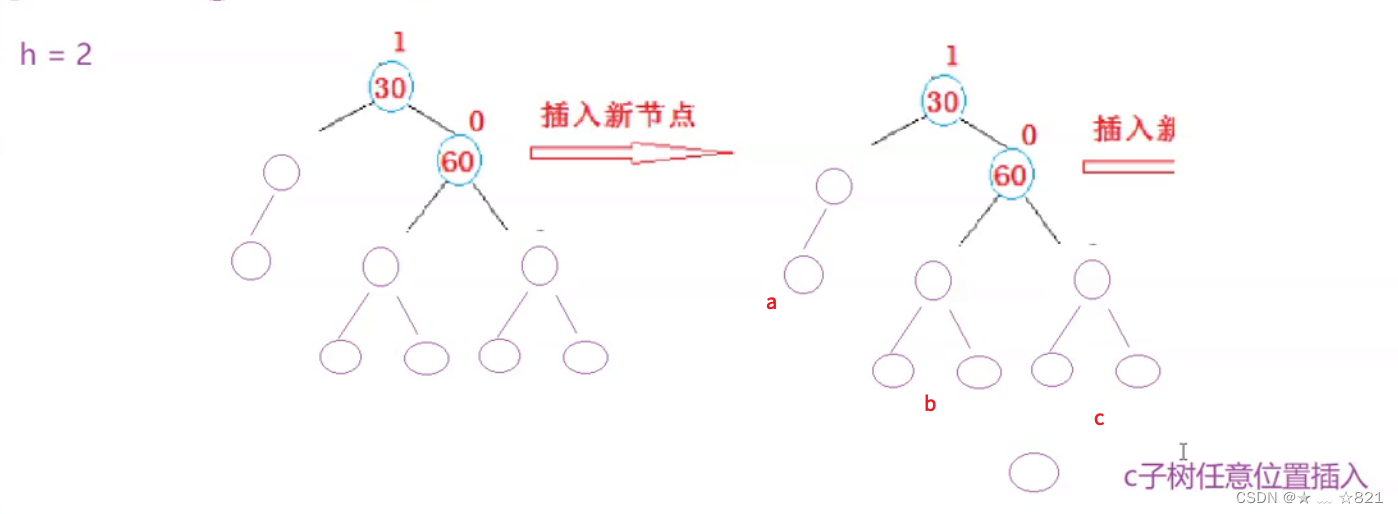
如果我们在C子树任意位置插入一个新节点,最后都会引发旋转。但是能够确定的是,C子树一定是Z这颗子树,否则当C子树插入新节点的时候,它C子树本身就要发生旋转了。其他a、b子树可以是x、y、z中的任意一种。
》如果h=3,那么情况就更复杂了,子树的组合就更多了。所以,我们就能抽象成长方条表示子树去替代。但是无论哪种情况都不需要担心,我们用同样的方法都可以将他们旋转出来,你右边高了,往左边压一压。
》无论你是多少种情况,都是一样的处理,怎么一样的处理呢?你右边不是太高了,我就要往左边旋转。我将b子树交给30这个节点,让30变成60节点的左边,这样你就均衡了,因为无论你子树的高度是多少,都是一样的处理。这个是右边高,左单旋:**b子树变成30的右子树,30变成60的左子树!*它这块做是有原则的。

它是要保证旋转的原则,1.保持搜索树的规则;2.子树平衡。首先我们b子树去做30节点的右子树有没有违反搜索树的规则呢?没有,因为b这颗树的节点一定是比60节点小,但是一定比30节点大,所以30. < b < 60,那么b去做30的右子树有没有毛病呢?是没有违反搜索的规则。那么30去做60的左子树好像也是可以的,30节点比60小,做60节点的左子树肯定是没问题呀,b子树又比30大,做30的右子树也没问题,b子树也比60节点要小,所以逗逼60节点小,那么就没有问题了!经过旋转旋转之后,就达到了平衡的效果。它这种旋转设计的很好,不需要考虑下面子树的情况,将他们作为一个整体来处理刚刚好。
》我们将这个代码写一下:我们来标记几个位置,30节点,我们标记为parent、60节点标记成subR(相当于市30节点的右孩子),b子树我们标记成subRL(b子树是subR的左子树,所以叫做subRL)
》首先,subR = parent->_right;subRL = subR->_left;我们刚刚讲了,parent的右子树要指向b子树,即parent->_right = subRL;parent要变成subR的左孩子,即subR->_left = parent;旋转之后,指针还是指向原来的节点,你只是改变了他们之间的关系哈,也就变成了如下:
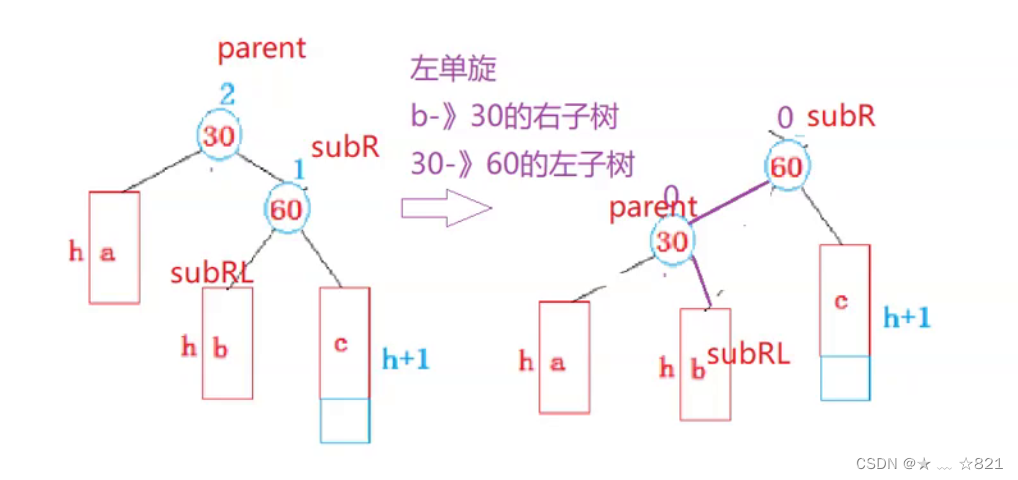
但是并不是这么简单,你是三叉链呀!你单单改变左右孩子是不够的,你还得更新他们父指针。所以subRL->_parnet = parnet;但是你这就掉陷阱了,因为subRL可能为nullptr空,所以你得提前先判断一下。subR->_parent = parent->_parent;parent->parent = subR;
》但是还是不够,因为parent你能确定它一定是root根吗?1.parent有可能是树的根;2.parent只是整棵树的局部子树,你旋转之后,parent的parent还是指向原来的,是不是就破坏了树的结构了呀。所以还有可能存在太上皇的存在,所以要判断一下parent是否为_root根,if(_root == parent)如果为根的话,那么就要更新一下_root,_root = subR,然后跟节点的parent指针本就是固定指向nullptr空的,_root = nullptr; 如果不为根的话,那么parent的parent的指针要指向subR,但是这里还有一种情况,我parent到底是左孩子还是右孩子呢,是不是又要判断一下,Node ppNode = parnet->_parnet;if(ppNode->_left = = parnet),ppNode->left = subR;else ppNode->right = subR;然后subR的parent是不是也要变成ppNode呀,即subR->parent = ppNode;
》下面就是要更新平衡因子了,我们发现parent的平衡因子一定是0,因为parent的左边是h,右边也是h,所以,parent->_bf = 0;60节点的平衡因子也是0,因为左边是h+1,右边同样是h+1,所以subR->_bf = 0;subRL我们没有动它的子树,所以它的平衡因子是不用更新的。
void RotateL(Node *parent)
{
Node *subR = parent->_right;
Node *subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node *ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (parent == ppNode->_left)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
//更新平衡因子
parent->_bf = subR->_bf = 0;
}
我们上面的RotateL()左单旋是什么情况才会要进行的呢?是不是当if(parent->_bf == 2 && cur->_bf = =1)的时候是需要我们进行左单旋呀,那么此时就是一个右边高,要进行左单旋呀----就是由平衡因子bf推出的嘛。
else if (parent->_bf == 2 || parent->_bf == -2)
// -1 or 1 -》 2 或 -2 插入节点导致本来高一边又变高了
{
if (parent->_bf == 2 && cur->_bf == 1) // 左单旋
{
RotateL(parent);
}
break;
}
》那么旋转完了之后要不继续向上更新呢?不需要了,因为插入节点之前,如果你是根就不需要动了,如果你不是_root根,那么在插入节点之前,那么ppNode的子树的高度为h+2(右子树,h为60节点的子树高度,然后2分别是parent、60节点这两个,所以ppNode的右子树高度为h+2),然后插入一个新节点后,ppNode右子树的高度就变成h+3了,然后我们要进行旋转,旋转之后,ppNode的右子树高度又变成了h+2!所以,我们旋转保持左右平衡的同时,也保证了树的高度不会发生变化,也就ppNode的子树的高度没有变化,那么旋转之后也不会对上层有影响,所以也就不需要向上更新了,那么就break跳出更新循环。
那如果现在是左边高了呢?

在a这个子树插入新节点,那么30节点的bf边成了-1,那么继而也会影响到60这个节点的bf变成了-2,这就是一个纯粹的左边高,那要干嘛?要进行右旋!我们可以画一个具象图来感受一下。
》当h1的时候
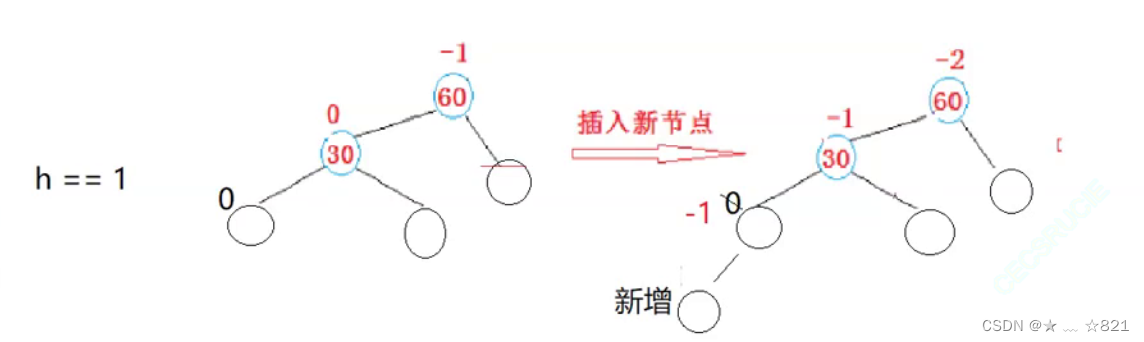
我们现在在a子树的左边或者右边插入都是无所谓的,都是会引发父节点30变成-1,60变成-2;
》当h2的时候呢:h为2的话,子树是有3种情况的
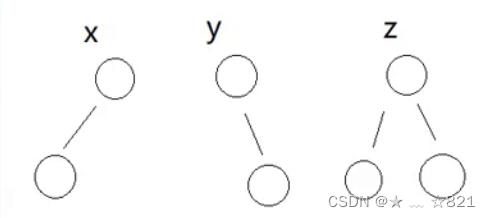
但是我们一定能够确定a这颗子树一定是Z这颗子树,不然a子树插入新节点的时候,那么它a子树本身就要发生旋转了。其他b、c子树可以是x、y、z中的任意一种。
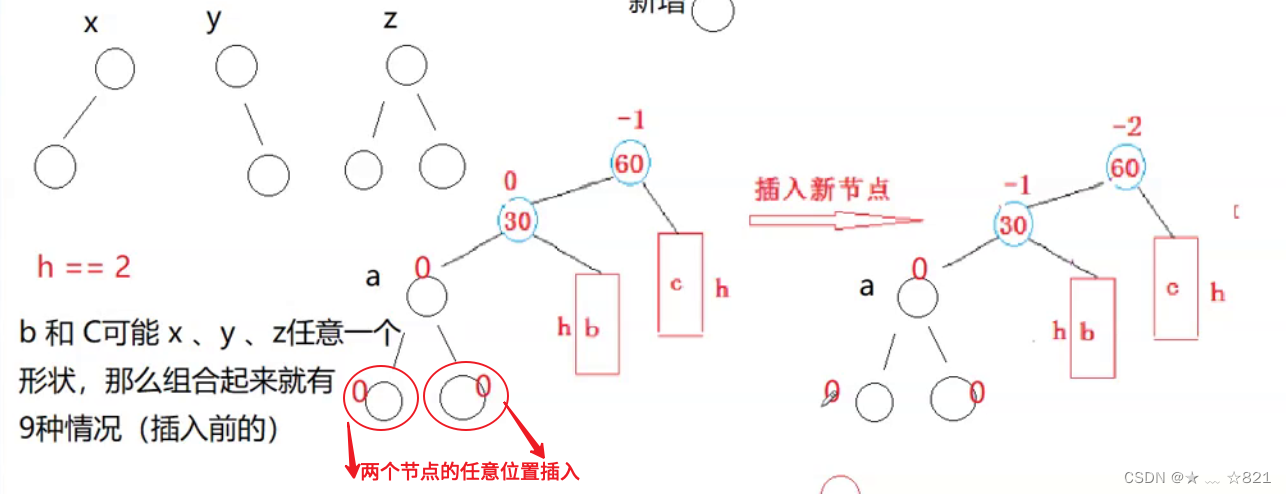
》在a子树的两个节点的任意位置插入都会引发az这个节点的bf变成-1,那么继而导致60节点变成-2进行旋转。也就是在a子树的2个叶子结点下面,任意孩子位置插入都会引发右单旋转,组合起来有36种情况。(两个叶子结点插入有4种,然后b、c可以是x、y、z中的任意一种,组合就是36种情况。)所以,我们想表达的就是太复杂了,具象的情况太情况了,所以,我们采取抽象图来解决。
》右单旋又是怎么样变的呢?b变成60的左边,60变成30的右边,30变成这个子树的根。同样这样旋转之后也遵循搜索树的规则。
》那么我们来标记一下各个节点的名称,60节点为parent,30节点为subL,b子树为subLR。
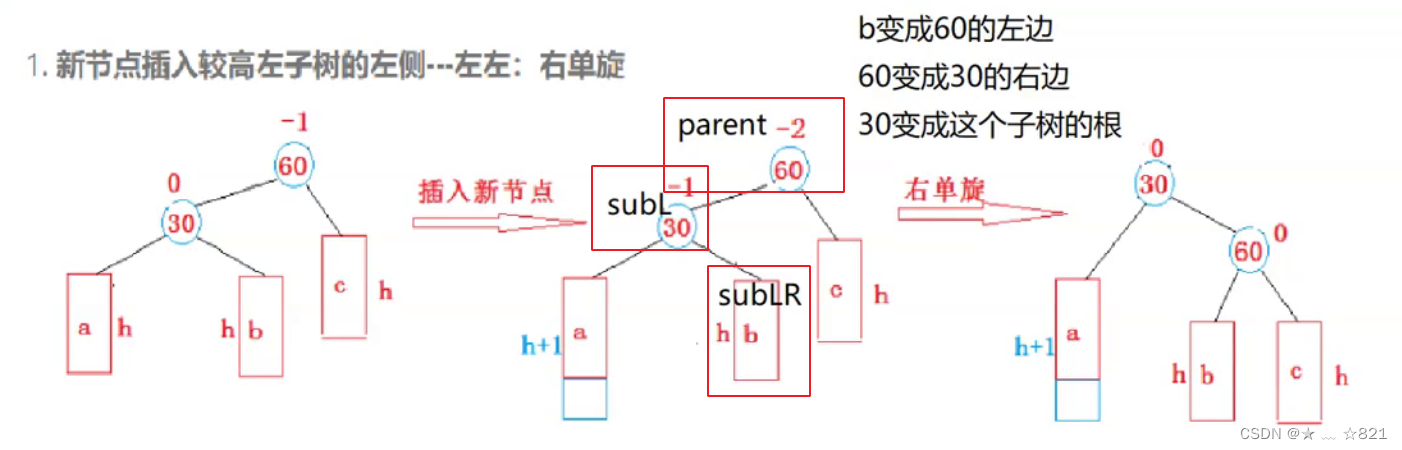
我们现在来进行编写RotateR()函数了:始终要记住旋转原则,1.保持搜索树;2.左右相对平衡。
》我们先来把subL、subLR定义出来,Node* subL = parent->_left;Node* subLR = subL->_right;然后我们来更新一下几个节点自身的关系,parent->_left = subLR;subLR->_parent = parent;subLR不能这么更新,因为你要考虑到它可能是nullptr空的情况,因为子树的高度h可能是0,但是subL和parnet都不可能为nullptr空,否则他们的平衡因子都不可能到-1、-2,所以,subLR要提前判断一下if(sunLR); subL->_right = parent;parent->_parent = subL;
》现在就剩下一个问题了,60如果原来是整棵树_root根的话,那么30就要变成整棵树新的_root根;如果60不是的话,那么他就是局部的子树,就要考虑到ppNode的问题。所以,我们在parent的_parent还没被修改之前,我们可以先保存ppNode指针,即Node* ppNode = parent->_parent;所以我们来判断是不是根的情况,if(parent == _root)那么30节点就是新的根了,_root = subL;_root->_parent = nullptr;如果parent不是根,那么就要改变ppNode的指针关系,同时也先要进行判断parent是ppNode的左子树还是右子树,所以,if(ppNode->_left = = parent)ppNode->_left = subL;否则,ppNode->_right = subL;然后再更新一下subL的_parent父指针,subl->_parent = ppNode;
》接着就树要更新平衡因子了。谁的平衡因子bf需要更新呢?只有subL和parent,因为只动了它们两个,并且他们的平衡因子bf都变成了0,subL->_bf = parent->_bf = 0;同上面左单旋的一样,ppNode的子树高度没有发生变化,也就不需要再向上更新平衡因子了。
》那么什么情况下要进行右旋呢?一定是(parent->_bf = =-2 && cur->_bf = = 1)情况下,也就是单纯的左边高。旋转后相比之前,树的高度不变,那么我们就不必向上更新平衡因子了,就break;
》两种旋转就都讲了,还有两种旋转,我们马上就开始。
我们上面的两种情况是一种比较基础简单的情况,如果在一些比较复杂的情况,有时候插入的时候就会出现一些怪异的情况,比如说,我们按8、6、7插入,就会呈现这样的情况:

如果你此时还是按照单旋的方式去旋转,你会发现旋转出来会有问题:
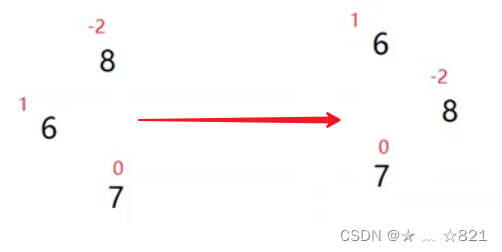
旋转之后并不平衡,所以不能用我们的单旋去处理。这种情况不是单纯的左边高,对于8而言是左边高,对于6而言是右边高,所以他这里的高度差是一个折线,我们前面的两种情况的高度差是一条直线。
》我们要换成另外的一种抽象图,变得比之前的抽象图还要复杂一点点:

这里是抽象图,我们用具象图来分析一下:
》当h=0时:b、c都不存在,我们在60节点的左右插入都会引发90节点的旋转

当h=1时:b、c子树不存在,我们在新增的时候,是在b或者c的位置进行新增,引发旋转

我们再来摸一下更复杂的第三种情况,h=2的时候:
》那么a、d可能是x、y、z这三种里面的任意一种,无论你是b的子树,或者c子树插入,都会引发旋转。



所以有可能是在b子树或者c子树插入新增节点,都会不断更新平衡因子bf到90节点而引发旋转。
》再往下h=3、h=4…只会更加复杂。这里真正的问题是,无论h是多少,单纯的单旋已经是解决不了问题了。那我们如何来解决问题呢?这里是用到双旋转来解决这块的问题。
》它先以30节点为轴进行旋转,先对30进行左单旋,怎么旋转呢?将你60节点的左子树变成我30节点的右子树,然后30节点变成60节点的左边,60顶替30原来的位置。
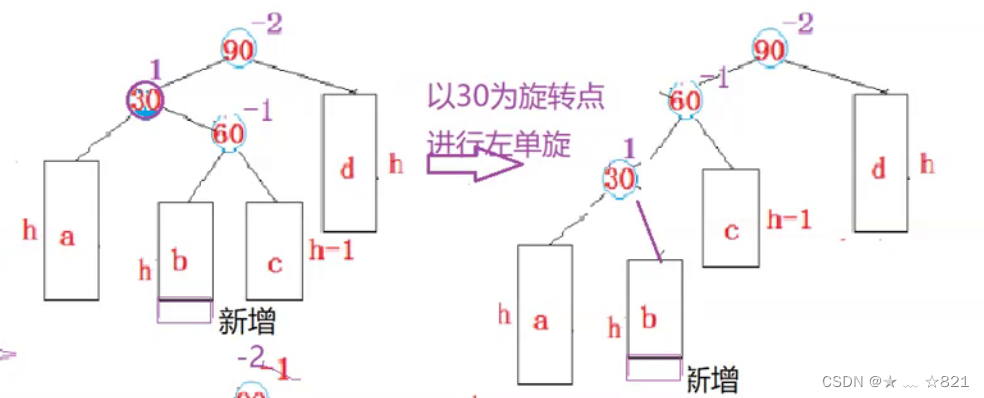
大家观察下,经过以30为旋转点进行左单旋后,你发现了什么呢? 这是不是变成纯粹的左边高了呀!是不是和我们上面的一个抽象图似曾相识呀。
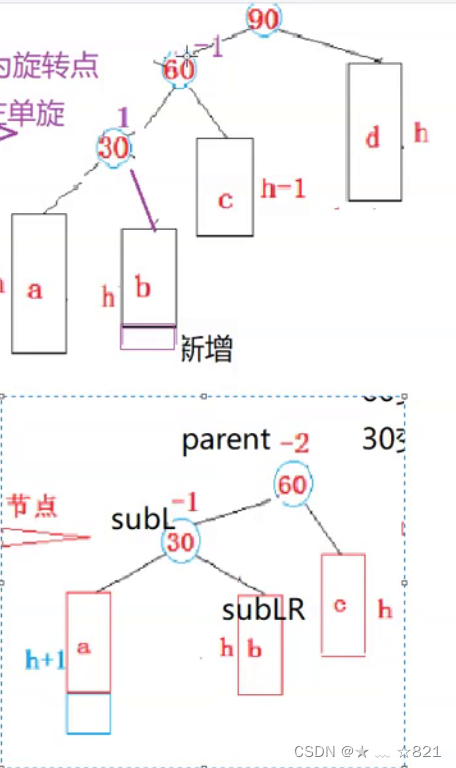
它们不完全一样,但是非常的像。我们现在要进行对90右单旋了。我们为什么要对30进行单旋呢?因为90是左边高,30是右边高,你30右边高,那么我对你来一个做单旋,是不是将你90节点这颗树变成纯粹的左边高呀,90节点和30节点都是左边高,我们是不是就可以进行右单旋了呀。
》我们对90进行右单旋了,让60节点的c子树变成90节点的左子树,90节点变成60节点的右子树,素以相当于90为旋转点进行右单旋,所以这就是一个左右双旋。
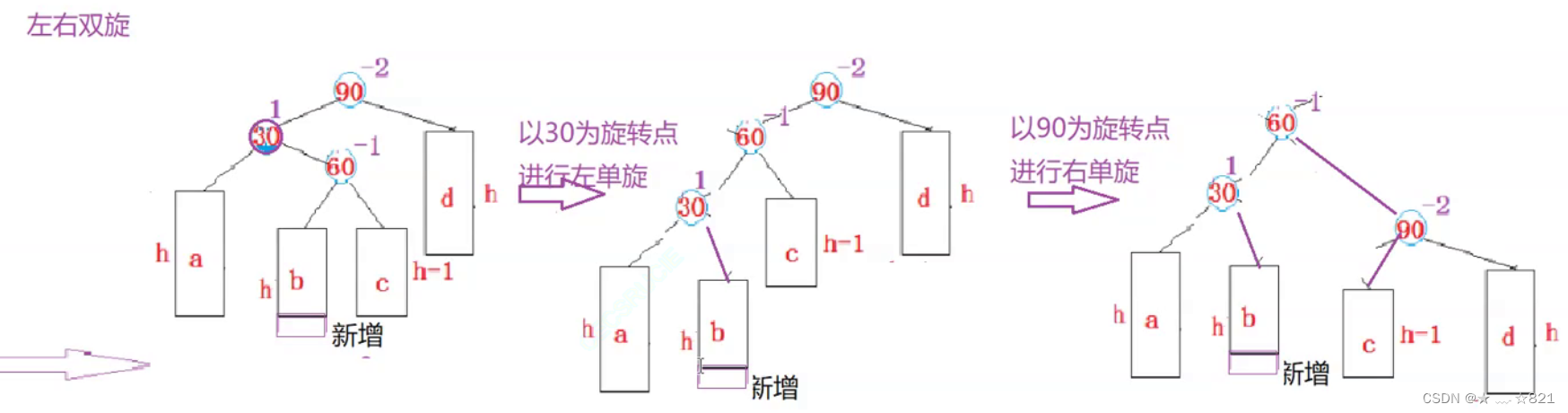
旋转完成之后,大家再来看看这颗树的高度变成什么样子了呢?旋转完成之后,我们是不是要单独来更新平衡因子bf呀,这可不简单了,因为30、60、90你都动了。
》60节点的平衡因子是多少呢?是0;30的bf呢?是0;90的平衡因子是多少?是1。在一开始,有一边是急剧的高,90的左边高很多,现在双旋之后便使得两边均衡很多了。
》刚刚是在b子树插入新节点,现在在c子树插入新节点其实差不多。还是一样对30进行左单旋, 让60对左子树变成30的右子树,30节点变成60节点的左子树,现在没必要更新平衡因子,等全部的旋转结束之后我们再更新也不晚。我们再以90节点来进行右单旋,将60节点的c子树给90的左子树,然后90节点变成60节点的右子树。如下图所示:
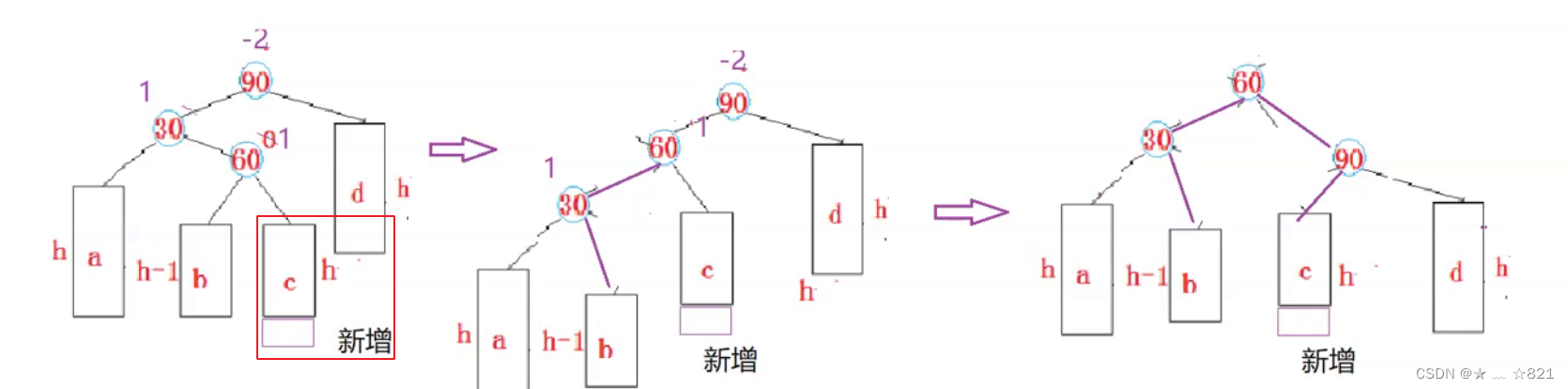
不管你的新节点是在b子树新增的,还是在c子树新增,60节点的平衡因子bf始终是0;30和90呢?因为你在b子树或者c子树插入新节点,所以,它们的平衡因子就不能确定了。为什么呢?因为,们如果新节点是在b插入,那么b这颗树的高度就是h ,a这颗树的高度也是h,所以b-a=0,那么30节点的平衡因子就是0;但是你如果没有在30的子树插入新节点的话,那么30节点的平衡因子bf就是-1。
》你在c子树插入新节点了,那么c这颗树的高度就是h,对于90节点来说,它的d这颗树的高度也是h,随意d-c=0,那么90节点的平衡因子bf就是0.
》也就是说,你在b或者c位置插入新节点,它们的节点大致位置形状都是不变的,但是平衡因子的更新是不一样的,需要区分开来看待。
》在这个双旋里面,谁是最大的赢家呢?是不是60这个节点呀,它被顶替在了原来树的根位置,然后30、90节点都做了它的左右孩子,然后60的左右孩子都分别分给了30和90,60的左孩子给了30节点的右边,60的右孩子给了90的左边,都符合搜索树的规则。
》但是,这里还有一个特殊情况没有分析到位, 哪一种呢?我们是不是都一开始就是在60的左右子树去新增节点呀,还有一种特殊情况,不是在60的左右子b、c子树去新增节点,而是60自身就是作为新增节点的情况我们没有考虑到,也就是h=0的时候,那么b、c子树就根本不存在。

60是新增节点就会引发这里的双旋,那这个双旋之后是个什么样子呢?还是一样,先来一个左单旋,然后再进行右单旋,最后所有节点的平衡因子更新都是变成了0。

我们现在来进行处理一下代码的问题吧;
》当parent的bf为-2,cur的bf为1的时候,即if(parent->_bf == -2 && cur->_bf = = 1),就认为是一个折线,就需要左右双旋。在进行双旋转之前,我们的整棵树高度是h+2,当双旋完之后整棵树的高度还是h+2,所以对于ppNode的平衡因子没有任何影响。
》双选装怎么写呢?void RotateLR(),我们是可以复用我们前面的单旋。我们来进行对节点做标记一下,90节点为parent,30节点为subL,60节点为subLR;我们是先对30节点进行左单旋,需要自己写嘛?直接复用RotateL(parent->_left),然后再进行右单旋,RotateR(parent);但是我们复用的是单旋,我们单旋的时候,它是会将我们节点的平衡因子都调整为0,也就是30、60、90节点的平衡因子bf都是会被修改成0,这样对吗?不对的!我们需要再自己来进行调整平衡因子。
void RotateLR(Node *parent)
{
RotateL(parent->_left);
RotateR(parent);
}
》这里调节平衡因子,是不是先分为,h = 0一种情况(就是上面说的特殊情况),h > 0是不是另外一种情况了呀。当h = 0最简单,所有节点的平衡因子都是0,但是我怎么知道h=0呢?它们有一个特别特别的特征,那就是60的平衡因子!如果60的平衡因子是0,那么60节点自己是新增节点,因为只有自己是新增节点,自己的bf才是0,如果是60的子树进行新增,那么我肯定不会为0的。所以60节点是0的话,那么就是h = 0,60自己是新增节点;如果60节点的平衡因子bf为1,那么就是在c子树插入;如果60节点的平衡因子是-1,那么就是在b子树插入新增节点。
》所以,我们使用60的平衡因子就可以区分3种插入新节点的情况,然后进而进行调整平衡因子了。我复用单旋的时候,和我是3种情况的哪一种又没有关系?没关系呀,单旋的时候只是改变节点的位置关系,我处理的干干净净。
》我们再说一下,60的左子树给了30的右子树,60的右子树给了90的左子树,然后30、90分别做了60的左右子树。我们下面来进行处理,我们先来标记一下,90节点为parent,30节点为subL,60节点为subLR。
》我们复用的单旋,悄悄的将我们的3个节点的平衡因子bf更新了,我们提前先将我们的subL、subLR都记录下来,NodesubL = parent->_left;Node subLR = subL->_right;这个subLR一定是不为空的,因为如果为nullptr空的话,那么parent的平衡因子也就不可能为-2了。我们还得提前记录一下subLR平衡因子,int bf = subLR->_bf;这个subLR的平衡因子是不是可以帮助我们进行判别是3种情况的哪一种插入情况呀!
》我们如何在两次单旋之后更新平衡因子bf呢?如果h = 0(60节点为新插入节点),那么我们复用的单旋是不是就对了呀,我们不要依赖它,万一人家单旋哪天不支持了呢?所以h0的情况我们也要单独处理一下。
》if(bf == 0)是不是就直接将parent、subL、subLR的平衡因子bf都是0呀;
》如果平衡因子1,if(bf ==1)是不是就代表新节点是在c子树插入的呀,然后经过两次单旋之后,c子树变成了90节点的左子树,然后90节点的平衡因子变成多少了呢?是不是就变成了0呀,此时你30的平衡因子就是-1呀,因为60节点的b子树给了30节点的右子树高度为h-1,所以算下来是-1。
》如果平衡因子bf = =1,if(bf= =-1),那么就 跟上面那一个情况反过来,经过双旋之后,30节点的平衡因子bf变为0,90节点的平衡因子变为-1;

我们把另外一种旋转再分析一下:
同样的在b或者c子树进行插入新增节点,当然或者60节点本身就是新增节点,这三种插入情况哈。
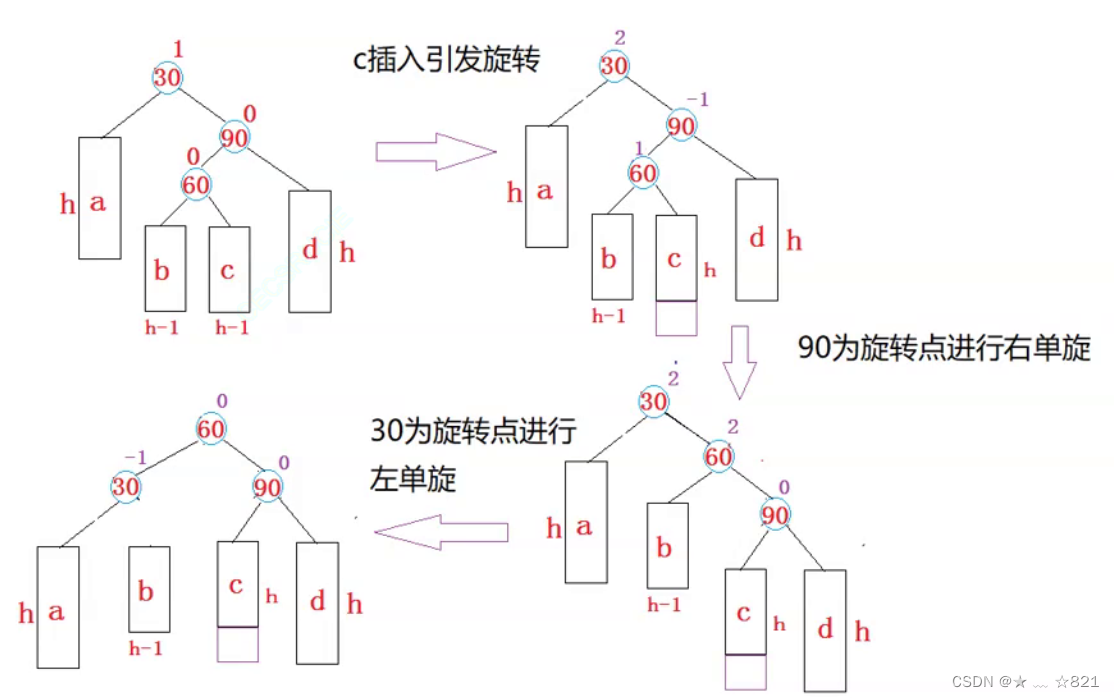

我们还是来将3个节点进行标记一下,30节点为parent,90节点为subR,60节点为subRL。

我们可以在AVL树里面搞一个球高度的函数,int _Height(Node* root);我检查我的AVL树怎么检查呀,我检查我的左子树,检查我的右子树,我将左右子树的高度一减,看有没有超过标准不就行了吗。求高度是不是一个后序的方式呀,要求我当前树的高度,我先去求我左树的高度,再去求右树的高度,然后我这颗树的高度是左右里面大的+1。
int _Height(Node *root)
{
if (root == nullptr)
return 0;
int lh = _Height(root->_left);
int rh = _Height(root->_right);
return lh > rh ? lh + 1 : rh + 1;
}
然后我们要检查我们是不是平衡树bool _IsBalanceTree(Node* root),如果是空树root == nullptr,那么是平衡树。如果不为空树,那么,求左子树高度和右子树高度,然后两个高度进行相减,int diff = rightHeight - leftHeight;if(abs(diff) >= 2)那么就是违反规则;还有一种导致不为平衡树的就是,虽然我的平衡因子没有>=2,但是自己的平衡因子bf和算下来的diff不相符合,那么也是一种不为平衡树的情况。在检查完自己是不是平衡树后,我们再递归去检查我的左子树和右子树是否为平衡树。
bool _IsBalanceTree(Node *root)
{
// 空树也是AVL树
if (nullptr == root)
return true;
// 计算pRoot节点的平衡因子:即pRoot左右子树的高度差
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
int diff = rightHeight - leftHeight;
// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者
// pRoot平衡因子的绝对值超过1,则一定不是AVL树
if (abs(diff) >= 2)
{
cout << root->_kv.first << "节点平衡因子异常" << endl;
return false;
}
if (diff != root->_bf)
{
cout << root->_kv.first << "节点平衡因子不符合实际" << endl;
return false;
}
// pRoot的左和右如果都是AVL树,则该树一定是AVL树
return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
AVL树的删除比插入更加复杂,当时我们在搜索树进行删除的时候都很费劲,我们高阶数据结构就不讲删除了,不需要掌握,当然可以了解。我们插入就已经能够帮助我们去理解它是如何进行平衡的了,包括我们后面要讲的红黑树和b树都不需要去掌握删除。我们学这些意义不是写出来,而是要很了解他的内部。