DAY22：二叉树（十二）二叉搜索树最小绝对差+二叉搜索树中的众数

news2024/11/25 16:18:58

文章目录

    • 530.二叉搜索树的最小绝对差
      • 思路
      • 完整版
      • 双指针优化写法：不用创建数组遍历
        • pre = root为什么是指向当前遍历的前一个节点
    • 501.二叉搜索树中的众数（这道题要知道普通二叉树怎么写）
      • 思路
      • 完整版
      • 普通二叉树的写法
        • sort自定义比较函数cmp的情况
        • 对比：优先级队列自定义比较函数的用法
          • 1.是否定义为类的区别
          • 2.升降序的区别
        • sort什么情况下需要自定义比较函数
        • 关于sort的底层实现与降序自定义
        • vector赋值:只要数据类型相同，就可以直接赋值
        • pair类型的<key,value>访问问题
        • debug问题：sort的cmp必须声明为static静态变量

530.二叉搜索树的最小绝对差

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

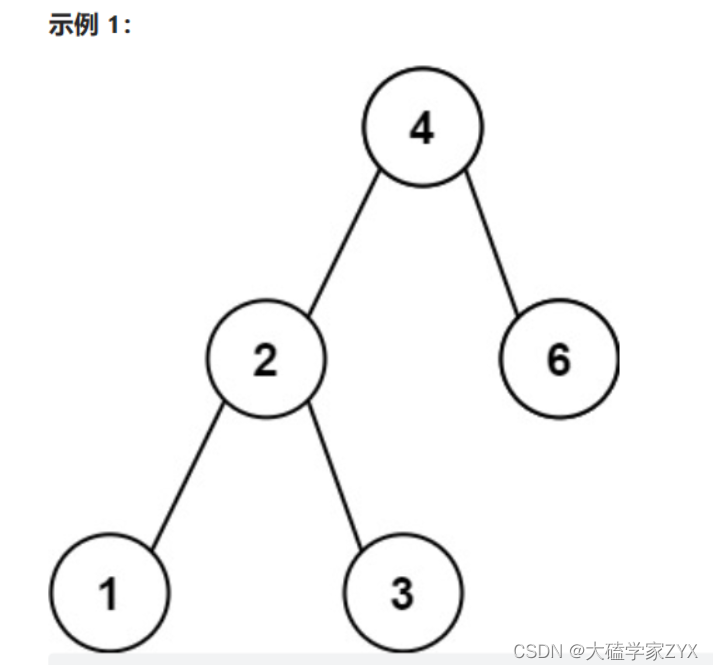
在这里插入图片描述
输入：root = [4,2,6,1,3]
输出：1

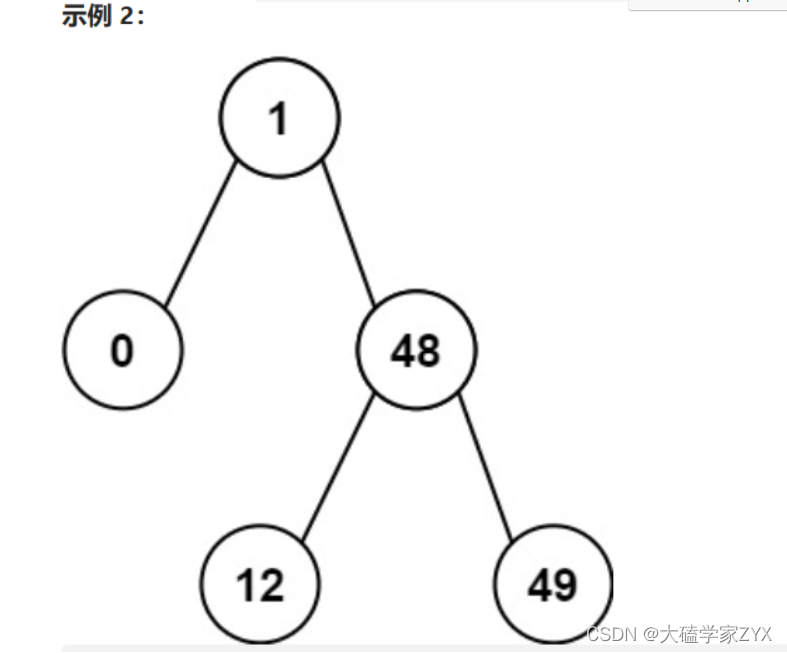
在这里插入图片描述
输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

  • 树中节点的数目范围是 [2, 104]
  • 0 <= Node.val <= 105

思路

BST是有序序列，有序序列求最小绝对差，可以直接转变成求相邻元素的最小绝对差！

因此可以先把BST存放到nums数组里，再求数组相邻元素最小绝对差

完整版

  • 这道题主要是把最小绝对差转换成相邻元素的绝对差
class Solution {
public:
    vector<int>nums;
    void travelsal(TreeNode* root){
        if(root==nullptr){
            return;
        }
        travelsal(root->left);
        nums.push_back(root->val);
        travelsal(root->right);
    }
    
    int getMinimumDifference(TreeNode* root) {
        if(root==NULL){
            return 0;
        }
        //中序遍历存入数组
        travelsal(root);
        //求相邻元素最小绝对差
        int result=INT_MAX;
        int difference = 0;
        for(int i=0;i<nums.size()-1;i++){
            difference = nums[i+1]-nums[i];
            if(difference<result){
                result = difference;
            }
        }
        return result;
    }
};

双指针优化写法：不用创建数组遍历

双指针优化写法是直接采用两个指针得出最小绝对差。

  • 两个指针分别指向当前节点和下一个节点，再用result记录差值里面的最小值
class Solution {
public:
    //全局变量
    int result = INT_MAX;//记录差值最小值
    TreeNode* pre = nullptr;
    void travelsal(TreeNode* root){
        if(root==nullptr)
            return;
        }
        //左
        travelsal(root->left);
        //中：比较差值
        if(pre!=nullptr){
            //取相邻元素差值更小的值
            result = result>abs(root->val-pre->val)?abs(root->val-pre->val):result;
        }
        //让pre指向当前遍历节点的前一个节点
        pre = root; 
        //右
        travelsal(root->right);
    }
    
    int getMinimumDifference(TreeNode* root) {
       if(root==nullptr){
           return 0;
       }
        travelsal(root);
        return result;
    }
};

pre = root为什么是指向当前遍历的前一个节点

最开始pre是空的，不走比较逻辑直接赋值pre = root；

root->left开始执行之后pre的赋值是在比较之后的，所以pre在比较的时候，一直是当前遍历节点的前一个节点

501.二叉搜索树中的众数（这道题要知道普通二叉树怎么写）

  • 本题也是二叉树中的双指针解法的应用
  • BST对于寻找频率最高的元素的特殊解法
  • 本题普通二叉树的写法不太简单，是一道cpp语法考察题，考察点较多需要复盘

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

在这里插入图片描述
输入：root = [1,null,2,2]
输出：[2]

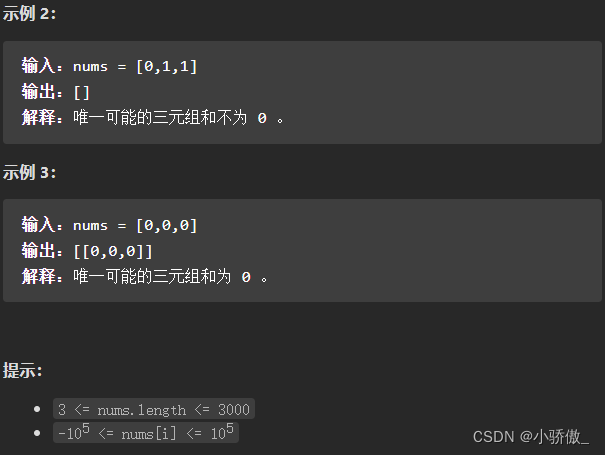
示例 2：
输入：root = [0]
输出：[0]

提示：

  • 树中节点的数目在范围 [1, 10^4] 内
  • -10^5 <= Node.val <= 10^5

思路

本题重新定义了二叉搜索树，里面可以有重复的元素。

如果本题不是二叉搜索树，我们需要用map来对二叉树元素出现的频率进行统计，统计完了再把频率进行排序，把map转换成vector输出频率最高的元素。注意众数不止一个。

由于本题是二叉搜索树，因此他的中序遍历是有序的，一样的数字一定是排在一起的。

提到二叉搜索树遍历顺序一定是中序遍历。

完整版

  • 本题的关键在于，如何只遍历一遍二叉树，就得到最高频率和所有等于最高频率的数值
  • 能够遍历一遍就得到频率最高的所有数值，主要是利用了BST的中序遍历有序的特性，本题重新定义的BST中，如果有相同元素，一定排列在一起
  • 注意这里面的细节和关键点，第一遍写最好把注释写上再写逻辑，很多代码容易漏掉
class Solution {
public:
   vector<int>result;
    int maxCount=0;
    int count = 0;
    TreeNode* pre=nullptr;
    
    void travelsal(TreeNode* root){
        if(root==nullptr){
            return;
        }
        //左
        travelsal(root->left);
        //中
        
        //首先累计count的值
        if(pre!=nullptr&&pre->val==root->val){
            count++;
        }
        else if(pre==nullptr){
            count=1;
        }
        //关键点1：如果不是前后相等的话count直接=1
        else{
            //如果不是前后相等，直接置为1
            count=1;
        }
        
        //更新pre，这一步也不能漏掉
        pre = root;
        
        //判断count是不是等于最大值
        if(count>maxCount){//如果计数大于最大频率
            maxCount = count;
            //关键点2：之前的数值要删除，并且加入新的数值
            //不能漏掉加入新数值！第一遍输出是空，就是漏掉了push_back
            result.clear();//之前的数值失效
            result.push_back(root->val);
         }
        //关键点3：相等就直接加入result结果集
        else if(count==maxCount){
            result.push_back(root->val);
        }
        //右
        travelsal(root->right);     
    }
    
    vector<int> findMode(TreeNode* root) {
        if(root==nullptr){
            result[0] = 0;
            return result;
        }
        travelsal(root);
        return result;
    }
};

普通二叉树的写法

  • 注意sort自定义cmp函数的static声明问题

如果是普通二叉树，求众数且众数不止一个需要全部输出的情况，需要用map存下所有元素的频率，再把value数值放入vector中，找到最大值。

注意我们是不能直接对map中的value排序的，C++中如果使用std::map或者std::multimap可以对key排序，但不能对value排序。

所以要把map转化数组即vector，再进行排序。vector里面放的也是pair<int, int>类型的数据，第一个int为元素，第二个int为出现频率。

  • 因为map中的数据类型是pair<int,int>，所以sort的cmp需要重新定义
  • 键值对的pair类型并不是指针，访问键值对的value应该用a.second
class Solution { 
public:
   //遍历整棵树，用map统计频率
    //这里的遍历顺序不重要，只要全部遍历了就行
    unordered_map<int,int>map;
    vector<int>result;
    void searchTree(TreeNode* root){
        if(root==nullptr){
            return;
        }
        //此处用了前序
        map[root->val]++; //统计元素频率
        searchTree(root->left);
        searchTree(root->right);
    }
    //把统计出来的value进行排序，注意map不能直接对value排序
    //因为map中的数据类型是pair<int,int>，因此sort的cmp需要重新定义降序排列
    bool static cmp(pair<int,int>& a,pair<int,int>& b){
        //注意键值对的pair类型并不是指针，不能用->来访问
        if(a.second>b.second){
            return true;
        }
        else
            return false;
    }
    vector<int> findMode(TreeNode* root) {
        if(root==nullptr){
            result[0] = 0;
            return result;
        }
        searchTree(root);
        //把map里的数据存在数组里
    	vector<pair<int,int>>vec(map.begin(),map.end());
    	//对数组里的pair.second进行排序
    	sort(vec.begin(),vec.end(),cmp);
        //取最高value的元素key，此时数组vec中已经是value降序排好序的
        result.push_back(vec[0].first);
        //把vec中最高value元素存进result里
        for(int i=1;i<vec.size();i++){
            if(vec[i].second == vec[0].second){
                result.push_back(vec[i].first);
            }
        }
  		return result; 
    }

};

sort自定义比较函数cmp的情况

因为需要比较的map里面的元素是pair<int,int>类型，所以需要自定义比较函数

bool cmp(pair<int,int>& a,pair<int,int>&b){
    return a.second>b.second;
}
//vector的赋值
vector<pair<int,int>>result = (map.begin(),map.end());
//sort对vector进行排序，自定义cmp函数
sort(result.begin(),result.end(),cmp);

在我们自定义sort比较函数的时候，一般写法都是，降序排序的情况：

（注意此处降序的比较逻辑和优先级队列是相反的）

bool cmp(pair<int,int>& a,pair<int,int>&b){
    return a.second>b.second;
}

升序排序的情况：

bool cmp(pair<int,int>& a,pair<int,int>&b){
    return a.second<b.second;
}

对比：优先级队列自定义比较函数的用法

优先级队列自定义cmp与sort自定义cmp的区别：

1.是否定义为类的区别
  • 对于优先级队列（priority_queue），比较函数通常需要定义为类。这是因为 priority_queue 在内部使用堆来实现，需要通过重载操作符或自定义比较函数来确定元素的优先级。
  • 而对于普通的 std::sort 函数，比较函数可以是函数或函数对象，不一定需要定义为类。你可以根据需要选择使用函数或函数对象作为自定义的比较函数。

优先级队列中比较函数自定义类的用法：

在这个例子中，我们创建一个小顶堆，但不是通过元素本身的大小来排序，而是通过元素的绝对值来排序。

  • 优先级队列里面默认参数是大顶堆，创建小顶堆需要自己加上greater的参数
  • 如果是自定义数据类型or键值对容器pair类型，需要自定义myCompare类来写比较函数
  • 需要按照一定规则进行特定顺序排序的元素排序，也需要自定义myCompare类
#include <queue>
#include <vector>
#include <cmath>

class AbsCompare {
public:
    bool operator() (int a, int b) {
        return abs(a) > abs(b);
    }
};

int main() {
    std::priority_queue<int, std::vector<int>, AbsCompare> pq;
    pq.push(-4);
    pq.push(2);
    pq.push(-8);
    pq.push(5);
    
    while (!pq.empty()) {
        std::cout << pq.top() << " ";
        pq.pop();
    }

    return 0;
}

在上述代码中，我们首先定义了一个名为 AbsCompare 的类，并在其中重载了 operator() 运算符。这个运算符接收两个 int 类型的参数 a 和 b，然后比较它们的绝对值。如果 a 的绝对值大于 b 的绝对值，那么就返回 true，表示 a 应该位于 b 之后。

2.升降序的区别

对于 std::sort 函数，如果要按照升序进行排序，通常使用以下形式的比较函数：

bool cmp(pair<int, int>& a, pair<int, int>& b) {
    return a.second < b.second;
}

如果要按照降序进行排序，通常使用以下形式的比较函数：

bool cmp(pair<int, int>& a, pair<int, int>& b) {
    return a.second > b.second;
}

但是对于优先级队列，实现小顶堆（按升序排列），需要这么写

class mycomparison {
public:
    bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
        return lhs.second > rhs.second;
    }
};

实现大顶堆（按降序排列）:

class mycomparison {
public:
    bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
        return lhs.second < rhs.second;
    }
};

堆的自定义比较函数，比较大小的符号和sort自定义函数的升降序符号正好相反。

对于优先级队列（堆），默认情况下是大顶堆，也就是优先级高的元素会排在前面。

当需要定义小顶堆（升序）时，当前元素比较大的时候比较函数应返回 true 。而对于 std::sort 的升序排序，当前元素比较小的时候比较函数应返回 true 。

原因的解释在之前的博客。(1条消息) 堆(优先级队列)的比较运算与快速排序默认cmp函数的区别_大磕学家ZYX的博客-CSDN博客

sort什么情况下需要自定义比较函数

在C++中，当我们使用std::sort函数来排序容器（例如，vector、deque等）时，我们通常需要自定义比较函数（也叫做比较器）的情况包括：

  1. 对pair或tuple的特定元素进行排序。如你的例子，比如我们有一个pair的vector，我们想按照pair的第二个元素来排序，而不是默认的第一个元素。

  2. 对自定义数据类型进行排序。比如，我们有一个存储自定义类/结构的vector，我们想根据类/结构的某个特定属性来排序。例如，如果有一个存储学生信息的vector，我们可能想按照学生的分数或者姓名进行排序。

    struct Student {
    string name;
    int score;
};

bool cmp(const Student& a, const Student& b) {
    return a.score < b.score;
}

vector<Student> students;
// fill students...
sort(students.begin(), students.end(), cmp);

  3. 对容器进行降序排序。默认情况下，std::sort函数是进行升序排序的，如果我们想进行降序排序，我们就需要自定义一个比较器。

    bool cmp(int a, int b) {
    return a > b;
}

vector<int> nums = {1, 2, 3, 4, 5};
sort(nums.begin(), nums.end(), cmp); // nums: {5, 4, 3, 2, 1}

  4. 对字符串进行排序。比如，我们可能想根据字符串的长度，而不是默认的字典序进行排序。

    bool cmp(const string& a, const string& b) {
    return a.size() < b.size();
}

vector<string> strs = {"apple", "pie", "banana"};
sort(strs.begin(), strs.end(), cmp); // strs: {"pie", "apple", "banana"}

以上就是几种可能需要自定义比较函数的情况。当然，这只是一些常见的情况，实际上，只要默认的比较方式无法满足我们的需求，我们就可以考虑自定义比较函数。

关于sort的底层实现与降序自定义

在C++中，std::sort函数的第三个参数是一个可选的比较函数，其默认值是operator<（也就是升序）。这个比较函数定义了元素之间的顺序关系。

我们需要确保这个比较函数符合"strict weak ordering"的条件，它是一个比较复杂的概念，简单来说，就是当a<b为真时，b<a必定为假，这对于排序算法的稳定性非常重要。

在下面例子中，提供的比较函数是a>b。

bool cmp(int a, int b) {
    return a > b;
}
vector<int> nums = {1, 2, 3, 4, 5};
sort(nums.begin(), nums.end(), cmp); // nums: {5, 4, 3, 2, 1}

这看上去和我们通常认为的降序排序刚好相反，但实际上是正确的。因为std::sort函数默认实现的是升序排序（也就是说，当第一个参数小于第二个参数时，这两个参数的位置会被交换），所以如果我们想要实现降序排序，我们需要把比较函数定义为“第一个参数大于第二个参数”。

关于std::sort的底层实现，这取决于具体的C++标准库实现。实际上，C++标准没有规定std::sort必须使用哪种排序算法，只是规定它必须在平均情况下达到O(n log n)的时间复杂性。然而，大多数标准库实现都会使用一种或多种高效的排序算法，比如快速排序、归并排序或堆排序。其中，GCC的实现（至少到2021年）是使用一种叫做IntroSort的排序算法，这是一种结合了快速排序和堆排序的算法。

vector赋值:只要数据类型相同，就可以直接赋值

  • 只要数据类型相同，就可以用.begin()和.end()迭代器直接给vector进行赋值。

准确的说，只要源容器中的元素类型能被转换（隐式或显式）为目标容器中的元素类型，就可以使用begin()和end()迭代器将源容器的元素范围复制到目标容器。

例如，如果我们有一个std::list<int>，你可以将其元素复制到std::vector<int>，因为int可以被复制为int：

std::list<int> my_list = {1, 2, 3, 4, 5};
std::vector<int> my_vec(my_list.begin(), my_list.end());

但是，当数据类型不同的时候，不能直接复制。我们不能将std::list<int>的元素直接复制到std::vector<double>，因为int不能被直接复制为double：

std::list<int> my_list = {1, 2, 3, 4, 5};
std::vector<double> my_vec(my_list.begin(), my_list.end()); // 错误！

但是，如果有一个类型转换，仍然可以实现这一点：

std::list<int> my_list = {1, 2, 3, 4, 5};
std::vector<double> my_vec(my_list.begin(), my_list.end(), [](int i){ return static_cast<double>(i); }); // OK

在本题的例子中，std::map<int, int>::value_type是std::pair<const int, int>类型，这可以被隐式转换为std::pair<int, int>，因此你可以将std::map<int, int>的元素直接复制到std::vector<std::pair<int, int>>。也就是

vector<pair<int, int>> vec(map.begin(), map.end());

vector的构造函数接受两个迭代器，作为复制的范围。map.begin()和map.end()分别返回指向map第一个元素和最后一个元素之后位置的迭代器。因此，这行代码会将map中的所有元素复制到vec中。

pair类型的<key,value>访问问题

pair是数据类型，所以pair的value元素访问需要用a.second不能用a->second

debug问题：sort的cmp必须声明为static静态变量

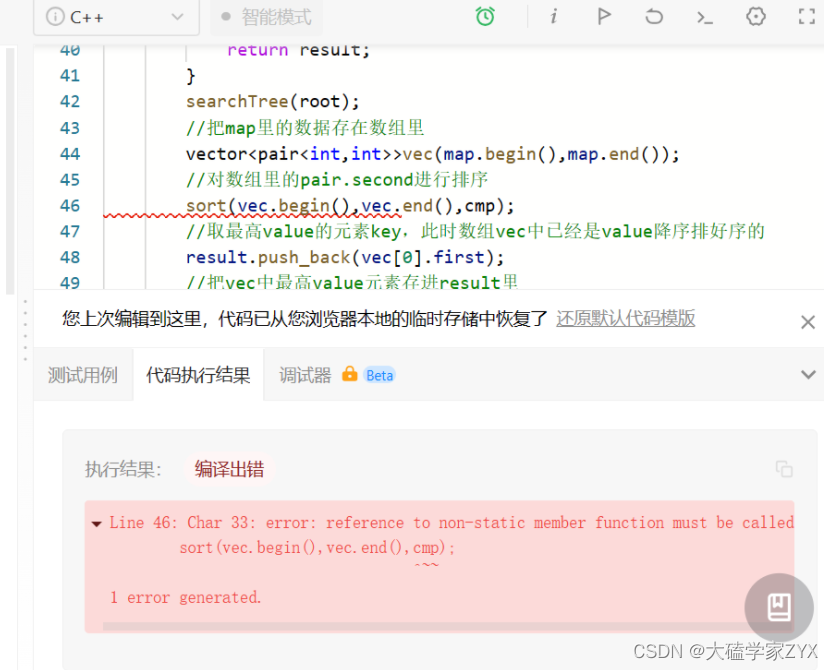
在这里插入图片描述
本题的cmp函数是类里面的成员函数，非静态的成员函数不能直接作为函数指针传入sort中。

解决办法是把cmp声明为static。static静态函数并不受类的实例限制，和全局函数是一样的。

详情见博客(1条消息) cmp报错: error: reference to non-static member function must be called sort(vec.begin(),vec.end(),c_大磕学家ZYX的博客-CSDN博客

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/644108.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[论文阅读笔记77]LoRA：Low-Rank Adaptation of Large Language Models

[论文阅读笔记77]LoRA：Low-Rank Adaptation of Large Language Models

1. 基本信息 题目论文作者与单位来源年份LoRA: Low-Rank Adaptation of Large Language ModelsmicrosoftInternational Conference on Learning Representations2021 524 Citations 论文链接&#xff1a;https://arxiv.org/pdf/2106.09685.pdf 论文代码&#xff1a;https://…
阅读更多...
IMX6ULL裸机篇之SPI实验

IMX6ULL裸机篇之SPI实验

一. SPI 实验 SPI实验&#xff1a;学习如何使用 I.MX6U 的 SPI 接口来驱动 ICM-20608&#xff0c;读取 ICM-20608 的六轴数据。 本文学习 SPI主控芯片的代码编写。其中&#xff0c;包括SPI工作模式设置&#xff0c;主从模式设置&#xff0c;时钟配置等实现。 二. SPI 主控芯…
阅读更多...
EBU5476 Microprocessor System Design 知识点总结_2 Arm architecture

EBU5476 Microprocessor System Design 知识点总结_2 Arm architecture

ARM架构 ARM是一个指令集&#xff0c;前面讲的几个汇编指令这些都算做指令。 ARM公司有意思的地方是&#xff0c;他们不做ARM设备&#xff0c;他们只设计指令集架构&#xff0c;然后授权&#xff08;知识产权核&#xff0c;IP核&#xff09;给其他半导体厂商做。 A&#xff…
阅读更多...
大数据分析与机器学习：技术深度与实例解析【上进小菜猪大数据系列】

大数据分析与机器学习：技术深度与实例解析【上进小菜猪大数据系列】

上进小菜猪&#xff0c;沈工大软件工程专业&#xff0c;爱好敲代码&#xff0c;持续输出干货。 大数据分析与机器学习已成为当今商业决策和科学研究中的关键组成部分。本文将深入探讨大数据技术的背景和原则&#xff0c;并结合实例介绍一些常见的大数据分析和机器学习技术。 …
阅读更多...
chatgpt赋能python：Python如何拟合直线：使用最小二乘法

chatgpt赋能python：Python如何拟合直线：使用最小二乘法

Python如何拟合直线&#xff1a;使用最小二乘法 在数据分析和机器学习领域&#xff0c;拟合一个最佳的直线是很常见和有用的。Python中有很多库可以拟合直线&#xff0c;但最小二乘法是其中最常用的一种方法。在本文中&#xff0c;我们将介绍最小二乘法的原理和如何在Python中…
阅读更多...
【Goalng 开源项目】还在手写重复的 CRUD 吗？这个开源项目帮你解放双手

【Goalng 开源项目】还在手写重复的 CRUD 吗？这个开源项目帮你解放双手

gormpher Gormpher 介绍快速开始WebObject 接口约定查询单条数据删除单条数据创建单条数据编辑单条数据条件查询多条数据 进阶WebObject 配置项动态接口函数Gorm 泛型函数Admin 源码handleEditObjecthandleQueryObject Gormpher 介绍 gormpher 是一个轻量级的 Golang 库 基于…
阅读更多...
编译原理及应用期末复习

编译原理及应用期末复习

杂 3型文法 右线性文法 短语、直接短语、句柄 、判断是否是二义性文法 1、证明是二义性文法&#xff1a;证明存在一个句子有两颗不同的语法树 ① 画语法分析树 ② 、NFA、DFA K&#xff1a;所有状态&#xff0c;包含初始状态 Σ&#xff1a;终结字符集 M&#xff1a;状…
阅读更多...
chatgpt赋能python：Python中替换字符串成int类型的方法

chatgpt赋能python：Python中替换字符串成int类型的方法

Python中替换字符串成int类型的方法 简介 在Python编程过程中&#xff0c;经常需要对字符串进行处理。有时候我们需要将字符串中的某些字符替换成int型数据&#xff0c;以便于进行一定的数值计算或其他操作。本文将介绍如何在Python中找出需要替换的字符&#xff0c;并将其转…
阅读更多...
Python实现将txt文件转换成对应的excel或csv文件

Python实现将txt文件转换成对应的excel或csv文件

前言 本文是该专栏的第29篇，后面会持续分享python的各种干货知识，值得关注。 工作上可能会遇到这样的情况，使用python将某个txt文本，按照行索引和列索引转换成对应的excel文件或者是csv文件。 那对于这样的需求，用python如何实现呢？跟着笔者直接往下看解决方法。（附完…
阅读更多...
UART协议总结

UART协议总结

UART&#xff08; Universal Asynchronous Receiver-Transmitter&#xff0c;通用异步收发器&#xff09;&#xff0c;是异步串行通信协议&#xff0c;用来传输串行数据。 1、UART原理说明 UART是全双工工作模式&#xff0c;其数据传输方法如下&#xff1a; 发送数据时&…
阅读更多...
Hive 和 Oracle 中 Decode 函数的用法差异

Hive 和 Oracle 中 Decode 函数的用法差异

前言 在数仓构建过程中，需要从业务那边进行数据的迁移！数仓大多数公司都是使用Hive，而业务那边使用的是Oracle数据库居多。最近就有个小伙伴在迁移的时候碰到了问题： 从报错来看，在使用 Decode() 函数的时候，传参有问题！ 既然问题来了，我们就来解决一下呗，只有不断地…
阅读更多...
基础知识学习---牛客网C++面试宝典（五）操作系统--第一节

基础知识学习---牛客网C++面试宝典（五）操作系统--第一节

1、本栏用来记录社招找工作过程中的内容&#xff0c;包括基础知识学习以及面试问题的记录等&#xff0c;以便于后续个人回顾学习&#xff1b; 暂时只有2023年3月份&#xff0c;第一次社招找工作的过程&#xff1b; 2、个人经历&#xff1a; 研究生期间课题是SLAM在无人机上的应…
阅读更多...
LeetCode_Day6 | 四数相加||、赎金信、三数之和、四数之和！

LeetCode_Day6 | 四数相加||、赎金信、三数之和、四数之和！

LeetCode_哈希表 454.四数相加1.题目描述2.思路3.代码实现 383.赎金信1.题目描述2.暴力法3.哈希法思路代码实现 15.三数之和1.题目描述 454.四数相加 1.题目描述 详情leetcode链接 2.思路 解题步骤&#xff1a; 首先定义 map&#xff0c;key放a和b两数之和&#xff0c;valu…
阅读更多...
神器CLIP：连接文本和图像，打造可迁移的视觉模型

神器CLIP：连接文本和图像，打造可迁移的视觉模型

2021年见证了vision transformer的大爆发&#xff0c;随着谷歌提出ViT之后&#xff0c;一大批的vision transformer的工作席卷计算机视觉任务。除了vision transformer&#xff0c;另外一个对计算机视觉影响比较大的工作就是Open AI在2021年1月份发布的DALL-E和CLIP&#xff0c…
阅读更多...
chatgpt赋能python：一、Python在数据可视化中的应用

chatgpt赋能python：一、Python在数据可视化中的应用

一、Python在数据可视化中的应用 Python是一种功能强大的编程语言&#xff0c;早已成为数据科学家和分析师的首选语言。数据可视化对于从数据中汲取信息和传达想法来说至关重要。Python也是数据可视化的理想工具之一。Python提供了许多强大的库&#xff0c;其中包括了一些流行…
阅读更多...
( 2023版)互联网 Java 工程师面试题及答案汇总

( 2023版)互联网 Java 工程师面试题及答案汇总

最近很多粉丝朋友私信我说&#xff1a;熬过了去年的寒冬却没熬过现在的内卷&#xff1b;打开 Boss 直拒一排已读不回&#xff0c;回的基本都是外包&#xff0c;薪资还给的不高&#xff0c;对技术水平要求也远超从前&#xff1b;感觉 Java 一个初中级岗位有上千人同时竞争&#…
阅读更多...
【野指针】

【野指针】

野指针 1. 指针是什么&#xff1f;2. 指针和指针类型2.1 指针-整数2.2 指针的解引用 3. 野指针3.1 野指针成因3.2 如何规避野指针 1. 指针是什么&#xff1f; 指针是什么&#xff1f; 指针理解的2个要点&#xff1a; 指针是内存中一个最小单元的编号&#xff0c;也就是地址平…
阅读更多...
MySQL性能优化：慢查询优化

MySQL性能优化：慢查询优化

一、执行计划 执行计划的语法 在SQL查询的前面加上EXPLAIN关键字就行。比如: EXPLAIN select* from order_exp;执行效果如下。 &#xff08;一&#xff09;参数详解&#xff1a; 1、id 在一个大的查询语句中每个SELECT关键字都对应一个唯一的id。我们知道我们写的查询语句一…
阅读更多...
【框架源码】Spring源码解析之BeanDefinition加载流程解析

【框架源码】Spring源码解析之BeanDefinition加载流程解析

观看本文之前&#xff0c;我们先思考一个问题&#xff0c;Spring是如何描述Bean对象的&#xff1f; Spring是根据BeanDefinition来创建Bean对象&#xff0c;BeanDefinition就是Spring中表示Bean定义。BeanDefinition用来存储Bean的相关信息&#xff0c;主要包括&#xff1a;Be…
阅读更多...
【Linux问题】删除用户时错把rm当成userdel删除后，该如何解决彻底删除?

【Linux问题】删除用户时错把rm当成userdel删除后，该如何解决彻底删除?

问题引入&#xff1a;之前创建的用户默认在home目录中&#xff0c;过了段时间以为是一个目录就直接使用rm删除了&#xff0c;结果在创建一个和之前用户同名的用户时发现报错&#xff1a;useradd: user ‘cjs’ already exists&#xff08;该用户已存在&#xff09;。 1、问题 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023