一、牛顿法

1.实质：牛顿法实质上是一种线性方法，其基本思想是将非线性方程f(x)=0逐步归结为某种线性方程来解。

2.牛顿法公式：

已知方程f(x)=0有近似解xk,假设，将f(x)在点xk泰勒展开，有则方程f(x)=0可近似表示为：，根为：则迭代法：

 

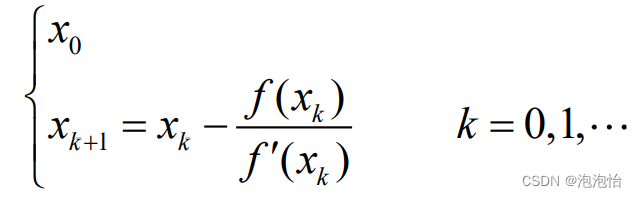
 3.牛顿法几何意义：

方程发f(x)=0的根可解释为曲线y=f(x)与x轴的交点横坐标，如图：

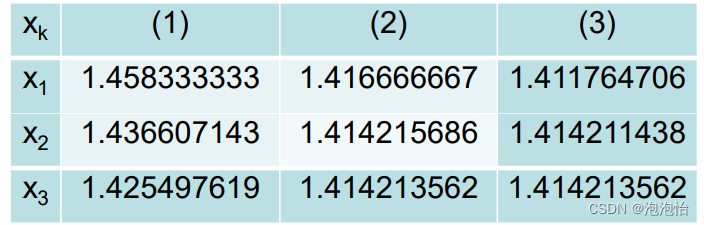
例题：

 

 牛顿法的优点是收敛快，缺点是计算量大且计算求导困难，并且只有初始近似x0在x*的附近才能保证收敛，若x0不合适可能不收敛。

二、牛顿法改进

1.简化牛顿法迭代公式：

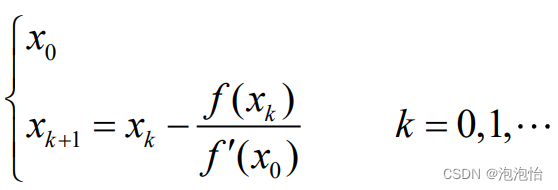
 2.几何意义：用斜率的平方弦与x轴的交点，做的近似。

3.牛顿下山法：

（1）基本思想：将牛顿法前后两次迭代结果进行加权平均，作为新的，并且保证，其中 为下山因子， ，选择 时， 从 开始，逐次将 减半进行试算，直到 满足 为止。

 （2）公式：

三、重根情形

设，且，则称是方程的m重根，则

 牛顿法：其中则，因则，则牛顿法线性收敛。

（1）改进一：

取其中m为几个重根，则则迭代法至少二阶收敛。

（2）改进二：

 若 是 的m重根，则 是 的m-1重根。 令 ，则 是 的单根，对 用牛顿法至少有二阶收敛性。 迭代公式如下：

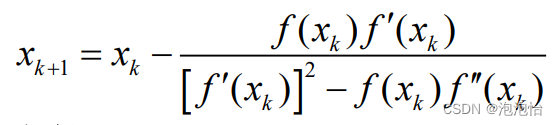
 例题：

 

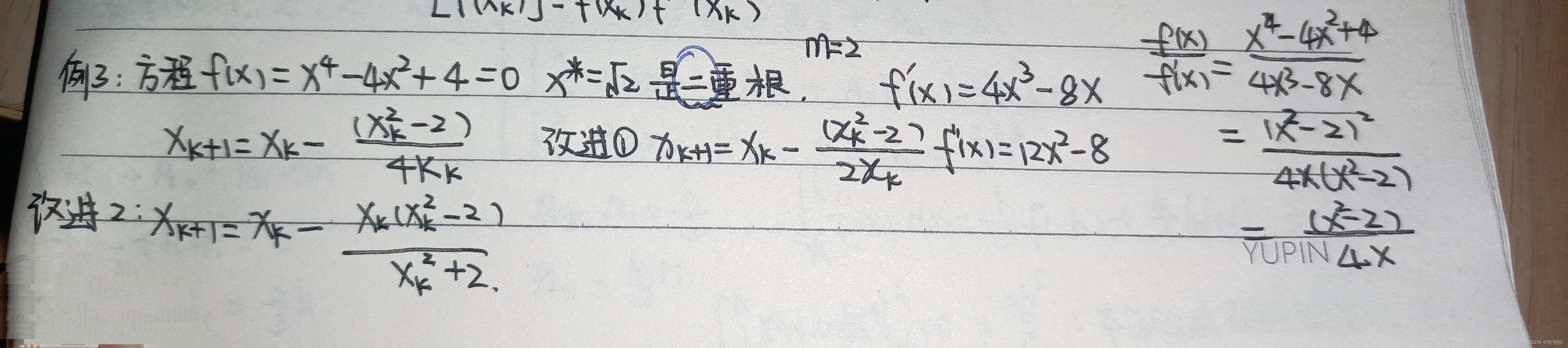
 结果：