🌈刷题，面试，求职，快来牛客网一起成为offer收割机！

点击注册收割offer

一、BM32 合并二叉树

描述

已知两颗二叉树，将它们合并成一颗二叉树。合并规则是：都存在的结点，就将结点值加起来，否则空的位置就由另一个树的结点来代替。例如：
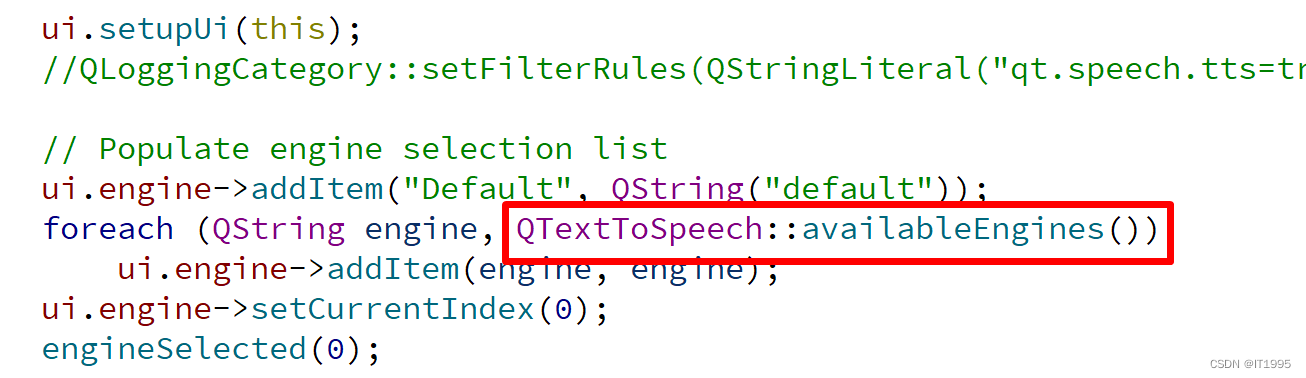
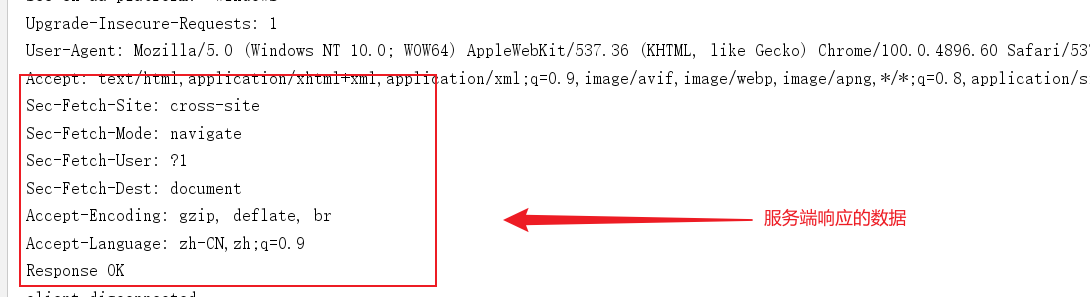
两颗二叉树是:
                                                   

 

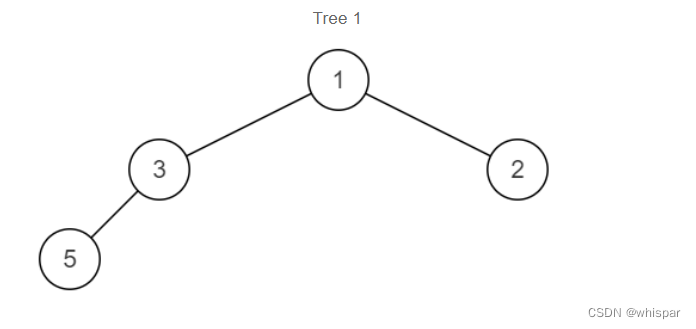
合并后的树为： 

 

 

数据范围：树上节点数量满足 0 ≤n≤500，树上节点的值一定在32位整型范围内。

进阶：空间复杂度 O(1)) ，时间复杂度 O(n)

点击下方链接，跳转做题🔻BM32 合并二叉树http://m6r.cn/QgJFm

思路：判断两棵树的相同位置的节点，以t1 树为基准树，当t1树的节点为空，t2树的节点不为空时，两者都不为空时，将t1.val + t2.val 即可  接下来t1 的左子树是：合并 t1左子树 t2左子树之后的左子树。t1 的右子树：是 合并 t1右子树 t2右子树之后的右子树，最终t1就是合并之后的根节点。

public class Solution {
    /**
     * 
     * @param t1 TreeNode类 
     * @param t2 TreeNode类 
     * @return TreeNode类
     */
    public TreeNode mergeTrees (TreeNode t1, TreeNode t2) {
        // write code here
        if(t1 == null){
          return t2;
        }
        if(t2 == null){
          return t1;
        }
        t1.val = t1.val + t2.val;
        t1.left = mergeTrees(t1.left,t2.left);
        t1.right = mergeTrees(t1.right,t2.right);
        return t1;
    }
}

二、BM31 对称的二叉树 

描述

给定一棵二叉树，判断其是否是自身的镜像（即：是否对称）
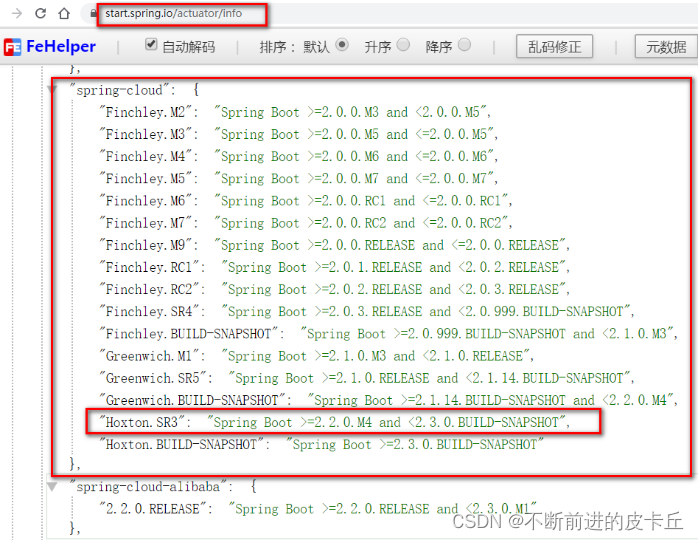
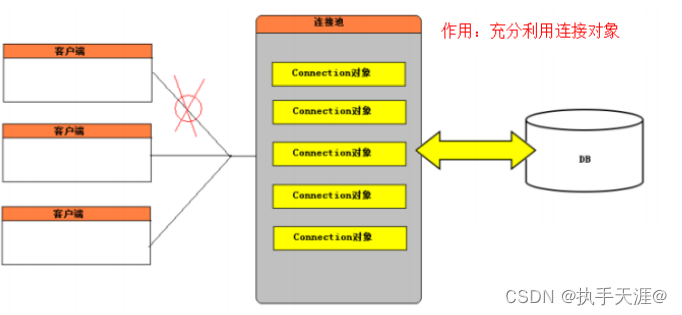
例如：                                 下面这棵二叉树是对称的

下面这棵二叉树不对称。

 

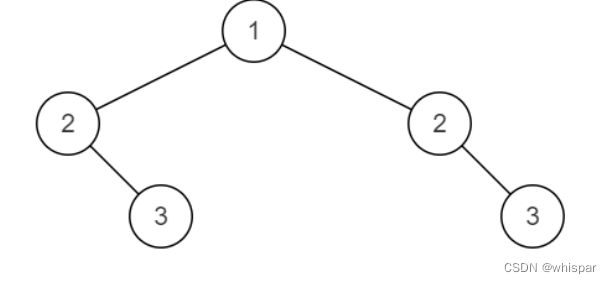
数据范围：节点数满足0≤n≤1000，节点上的值满足∣val∣≤1000

要求：空间复杂度 O(n)，时间复杂度 O(n)

BM31 对称的二叉树http://m6r.cn/j1t4i

思路：判断二叉树的左右树是否空，如果左树和右树都为空，则返回 true ,左子树为空，右子树不为空或者右子树为空左子树不为空返回 false，对应的左子树的val值与右子树的 val值不相等,返回false ，递归左子树的左节点和右子树的右节点即可

public class Solution {
    boolean isSymmetrical(TreeNode pRoot) {
      if(pRoot == null){
        return true;
      }
      return isSymmetricalChild(pRoot.left,pRoot.right);  
    }
    private boolean isSymmetricalChild(TreeNode leftTree,TreeNode rightTree){
      if(leftTree == null && rightTree == null){
        return true;
      }
      if(leftTree!= null && rightTree == null || leftTree == null && rightTree != null){
        return false;
      }
      if(leftTree.val != rightTree.val){
        return false;
      }
      return isSymmetricalChild(leftTree.left,rightTree.right)&&isSymmetricalChild(leftTree.right,rightTree.left);
    }
}

三 、 左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

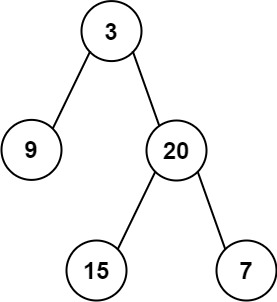
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

思路 ： 按照深读优先搜索，如果满足左节点的左右子树都为空即叶子节点时，将左叶子节点的 val 值储存在 sum中即可

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null){
            return 0;
        }
        Queue<TreeNode> qu = new LinkedList<>();
        qu.offer(root);
        int sumLeaf = 0;
        while(!qu.isEmpty()){
            TreeNode cur = qu.poll();
            if(cur.left != null){
               if(isLeafNode(cur.left)){
                   sumLeaf += cur.left.val;
               }else{
                   qu.offer(cur.left);
               }
            }
            if(cur.right != null){
              qu.offer(cur.right);
            }
        }
        return sumLeaf;
     }
    
    public boolean isLeafNode(TreeNode root){
        return root.left == null && root.right == null;
    }
}